V型皱褶芯材夹层结构强迫对流传热与热应力分析
周晨,王志瑾,候天骄
V型皱褶芯材夹层结构强迫对流传热与热应力分析
周晨1,王志瑾1,候天骄2
(1. 南京航空航天大学飞行器先进设计技术国防重点学科实验室;2. 南京航空航天大学航天学院:南京210016)
V型皱褶芯材夹层结构与强迫对流冷却相结合,可应用于高超声速飞行器或大功率电子器件承载和散热的多功能设计。文章采用数值仿真方法对强迫对流条件下V型皱褶芯材夹层结构的换热及其产生的热应力进行研究,获得了相应的速度场、温度场及结构热应力分布。结果表明:强迫对流条件下,V型皱褶芯材夹层结构的换热性能明显提高,同时导致较大的压力损失。流体速度场随着几何构型的改变而发生周期性的变化,在结构偏折处波峰一侧流速达到最大,对流换热得到增强;沿着冷却液流动方向,结构与冷却液的温度逐渐升高,并伴随着周期性的波动;皱褶芯材夹层结构的整体换热能力随着入口流速的增大而增强。热流输入侧的面板热应力和变形均较大,结构皱褶部位存在应力集中。
皱褶芯材;强迫对流;夹层结构;换热性能;热应力
0 引言
皱褶芯材是将平板基材按照一定规律的线系网格进行局部折叠而得到的一种具有周期性胞元构型的三维结构[1]。其设计思想源于手工折纸,从夹层结构出现之初就被提出用于芯材设计,但由于欠缺高效的生产制备工艺,对皱褶芯材的研究在相当长的一段时间内都处于停滞状态[2]。近年来,新型制备工艺[3-5]的诞生令皱褶芯材重新受到国内外研究人员的关注。王志瑾等对皱褶芯材几何设计方法[1]进行了研究,设计了平面皱褶芯材和单曲面皱褶芯材;针对皱褶芯材夹层板在隔声[6]、防热[7-8]及吸能[9]等方面进行了数值计算和实验研究。张延昌等[10]利用非线性有限元分析了皱褶芯材几何参数对结构耐撞性能的影响。Heimbs[11]和Fischer[12]等对皱褶芯材夹层板进行了一系列压缩、剪切和冲击的实验研究和数值仿真。皱褶芯材成型简单,可设计性强,在隔热、隔声等领域有着广阔的应用前景;同时,其开环的连续空腔构型使其具有优良的散热性能和流通性能[12-13],更有利于实现结构的多功能设计。
以多孔材料作为芯材的夹层结构通常具有至少一个方向的流动通道,采用强迫对流形式通入冷却液,可用于高超声速飞行器、发动机燃烧室或高功率电子器件等的主动冷却。高亮、孙雨果等[14-17]对点阵夹层结构的流动特性和换热特性进行了理论分析和数值模拟。Rakow等[18]分别从实验、数值分析和微观角度对强迫对流主动冷却下的金属泡沫夹层板进行了传热和结构热响应研究。Feng等[19-20]采用数值仿真和实验的方法研究了加装肋片的金属泡沫在强迫对流下的换热性能。王储等[21]建立了层板内部流动的数值模型,研究了层板几何参数及雷诺数对流动特性的影响。
本文以V型皱褶芯材夹层结构作为研究对象,采用数值仿真的方法研究了在以水作为冷却液的强迫对流条件下,该结构的传热以及相应的热-结构耦合问题。通过计算先后得到了V型皱褶芯材夹层结构的温度场及相应的结构应力场和变形场;根据结果分析了其流道中流体的流动特性,进一步探讨了对结构换热性能的影响机制;并对不同冷却液流速下该结构的总体换热性能进行了分析和评价。
1 模型描述
图1为典型的强迫对流冷却下的V型皱褶芯材夹层结构示意图。热量通过上面板传入夹层结构内部,沿方向通入冷却液利用强迫对流进行散热,从而提高结构承受热载荷的能力。如图1所示,V型皱褶芯材夹层结构的流道有2种类型:绿线所经过的正三角型流道(由芯材与下面板构成)以及蓝线所经过的倒三角型流道(由芯材与上面板构成)。
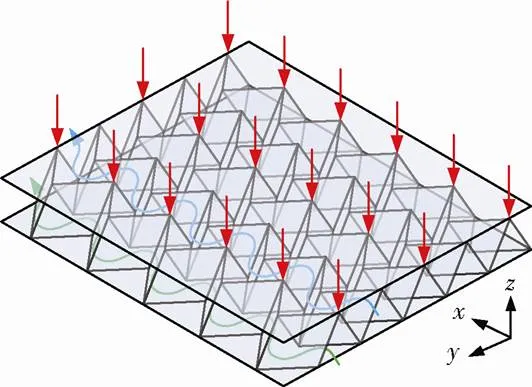
图1 受热V型皱褶芯材夹层结构强迫对流冷却示意
V型皱褶芯材胞元可由4个独立的参数表示[1],如图2(a)所示。在对有厚度的平板基材进行皱褶成型时,可能造成折痕位置出现局部缺陷或材料积聚[22]。假设有厚度的芯材经过皱褶后如图2(b)所示,本文所研究的V型皱褶芯材夹层结构的几何尺寸参数见表1,其中c和f分别为芯材和面板的厚度。

(a) V型皱褶芯材胞元示意
(b) 带厚度的V型皱褶芯材胞元示意
图2 V型皱褶芯材夹层结构胞元及几何尺寸示意
Fig. 2 Geometric parameters of a V-pattern folded core unit cell

表1 皱褶芯材夹层结构几何尺寸
本研究采用水作为冷却液,面板和芯材采用铝合金Al 2024-T851。根据初步分析可知,在本研究所涉及的温度变化范围内,铝合金材料属性变化不大,可假设夹层结构固体部分的热物理属性及力学性能不随温度发生变化,其相关性能参数[23]如表2所示。

表2 Al 2024-T851的物理性能参数
2 强迫对流共轭传热分析
2.1 耦合传热计算
强迫对流条件下,皱褶芯材夹层结构的共轭传热过程包括:流体的流动与传热、固体结构的热传导以及固体结构与流体之间的对流换热。本文采用Fluent软件对计算区域进行整场离散、整场求解。由于皱褶芯材与面板构成周期性的流道,为了减少计算量,对图1所示V型皱褶芯材夹层板沿向取1个周期(见图3)作为分析对象。

图3 简化后的周期模型示意
在进行数值模拟时,假设:1)流动和传热是稳态的;2)流体为不可压缩的牛顿型流体;3)忽略结构与周围环境的自然对流和辐射换热;4)不考虑黏性耗散热。
基于上述假设,流场的控制方程采用笛卡儿张量符号可表示为[24]:
连续方程:

式中为流体速度矢量。
动量方程:

式中:为冷却液的密度;为压力;τ为黏性应力张量,在不可压缩条件下可表示为
, (3)
其中为黏性系数。
能量方程:

式中:c、f分别为冷却液的比热容和热传导系数;f为流体温度。
对于固体区域,稳态导热微分方程可直接由式(4)在不计流体本身流动的情况下推导得到,

式中:s为固体材料的热传导系数;s为固体的温度。
状态方程:
=。 (6)
在固液界面上,根据温度和热流的连续性条件可得:

。 (8)
在Fluent共轭传热计算过程中,流体域和固体域采用通用的控制方程,即雷诺平均N-S方程(RANS),区别在于固体域只需求解能量方程即可。固-液耦合界面的对流换热系数由Fluent计算直接得到。选用RNG-双方程湍流模型,在近壁区域采用增强壁面函数进行处理。固体域采用结构化网格划分;流体域采用非结构网格划分,并在靠近壁面位置采用边界层网格进行局部加密。
2.2 热载荷和边界条件
在V型皱褶芯材夹层结构的上面板施加恒定的热流密度[25]=100000W/m2。沿流道方向(向)通入冷却液(水)对结构进行对流冷却,采用速度入口边界条件,入口处冷却液温度为0= 300K,流速0=0.1m/s;采用压力出口边界条件,出口处设置参考压力为0Pa。由于沿向只取了1个周期作为研究对象,所以向侧面均设置为周期性边界条件,固-液界面为无滑移、热耦合边界,其他壁面均设置为绝热壁面。
2.3 网格独立性验证
CFD计算结果是否准确很大程度上依赖于计算区域网格的划分。但是若网格密度过大,会造成计算量急剧增大。因此,需要在保证计算精度的前提下,尽可能地减少网格数量。本文对网格划分进行了独立性验证,针对多种网格划分方案分别进行了计算,图4给出了整体结构的平均努塞尔数随网格数量的变化曲线。可以看到,随着网格数量的增大,努塞尔数逐渐变大,当网格数量达到200000左右时逐渐趋于稳定。最终,本文采用的网格单元总数为185300。

图4 网格独立性验证
3 结构热应力分析
利用共轭传热分析得到的结构温度场作为载荷,给定边界条件,求解热弹性方程,得到相应的结构应力场和变形场,在不受外加机械载荷情况下的热弹性基本方程如下[26]:
平衡方程:

几何方程:
。 (10)
在温度发生变化的情况下,弹性体的应变由2部分组成:1)由于自由膨胀而产生的应变分量,即=Δ,对应的剪应变分量为0;2)在热膨胀时弹性体内各部分之间由相互约束产生的应变分量,它们与热应力之间满足胡克定律。因此,变温情况下的物理方程为

式(9)~式(11)中:σ为应力张量;ε为应变张量;为位移矢量;δ为克罗内克符号;s为柔度系数;为热膨胀系数;Δ为温度变化。
在热应力计算时,将上述流场与传热分析时得到的皱褶结构温度场作为载荷,入口端约束u=u=u=0,出口端约束u=0,上、下面板的向侧面则采用对称约束u=0。
4 仿真结果及分析
4.1 V型皱褶芯材夹层结构速度场
为了使仿真结果显示更加直观,图5~图9均沿向显示了5个周期。冷却液沿方向流入,由于面板和芯材的干扰和阻碍,其速度将不断发生变化;同时,由于V型皱褶芯材夹层结构在方向上也是周期排列,所以在稳态条件下,速度场将呈现周期性变化规律。
V型皱褶芯材夹层结构在几何构型上以胞元为单位,周期排列,在每个流道内,峰、谷依次交替。图5为流体区域紧靠上面板位置(=0.0109m)的截面速度分布云图。整体来说,速度分布随胞元发生周期性变化,进口和出口效应的主要影响区域均为约1个胞元的长度。图6为中间胞元在同一位置截面的平面速度分布矢量图,从图中可以看出,冷却液在峰前得到加速,随后一方面在峰后产生回流,另一方面继续加速直接冲击下游另一侧的峰前壁面。

图5 截面z=0.0109m上的速度分布云图

图6 中间胞元在截面z=0.0109m上的速度分布矢量图
图7为沿方向上各截面的速度分布云图,其中图7(a)为沿流动方向前4个胞元的中央截面,图7(b)为后3个胞元的出口截面。从图中可以清晰地看出,除了第1个和最后1个胞元外,中间各胞元在相对应的截面上速度分布基本一致。流体在波峰处流速最大;在波谷贴近固体壁面的位置,由于受到壁面黏性和下游芯材的阻碍,流速最低。

(a) 截面=0.015, 0.045, 0.075, 0.105m
(b) 截面=0.09, 0.12, 0.15m
图7 沿向各截面速度分布云图
Fig. 7 Velocity distribution at cross sections alongdirection
4.2 V型皱褶芯材夹层结构温度场
对于单相流体的强迫对流换热,强化传热最根本的措施就是减薄或破坏边界层,增强流体的径向混合[27]。图8为稳态下V型皱褶芯材夹层板的结构温度与冷却液温度分布云图。从图中可以看出,热量由上面板向下传递,当冷却液沿方向流过腔体时,与上、下面板及芯材进行换热,通过自身温度升高的方式存储能量,带走一部分原本将沿夹层板厚度方向传递的热量,从而有效降低了下面板的温度。沿冷却液流动方向,结构和流体的温度均不断升高,且温度载荷在夹层板厚度方向上的渗透不断加深,但渗透加深的速率逐渐减缓,这是由于参与下游换热的冷却液在上游已经得到了加热。

(a) 结构温度分布
(b) 冷却液温度分布
图8 结构温度及冷却液温度分布云图
Fig. 8 Temperature contours in structure and coolant
图9为沿方向各胞元截面上的结构温度与冷却液温度分布云图。从图中可以看出,由于上面板为热源输入侧,且直接构成倒三角流道的底边,所以在同一截面中,倒三角流道中冷却液的温度明显高于正三角流道中的冷却液温度。热量自上而下传递的过程中,在倒三角流道底边中部区域,通过与冷却液之间的对流进行换热;而在倒三角流道的两个底角区域,上面板与芯材相互接触,热量由芯材通过热传导的方式向下传递,同时面板、芯材均与冷却液进行对流换热,因此各截面的最大温度值均出现在倒三角流道的底边中部。此外,在出口截面上还有相当一部分冷却液温度较低,说明其利用率还可进一步提高。

图9 沿x向各截面温度分布云图
为了便于观察和比较结构温度分布,分别沿上、下面板外壁面向边界(参见图3)提取节点温度。图10为2种结构沿上、下面板2条路径(Polyline 1和Polyline 2)的温度变化曲线。其中横坐标为各节点对应的方向坐标。

(a) 沿上面板Polyline 1温度分布
(b) 沿下面板Polyline 2温度分布
图10 面板温度沿流动方向分布
Fig. 10 Temperature distribution along the flow direction
从图10可看出,上面板在入口端温度迅速上升,在最初半个胞元位置处出现峰值,而后温度先下降再缓慢上升,其中上面板的温度呈现出小幅度的周期性波动。冷却液平行于方向匀速流入,在前半个胞元内,以一种相对平稳的状态流动,流速较低(参见图5),因此该处对流换热较弱;随后由于流道发生偏折,皱褶芯材对来流形成阻碍和拖曳作用,冷却液径向运动加剧(参见图7),使得对流换热得到增强。图10(a)所对应的路径为图3中的Polyline 1,该路径位于倒三角流道的中线在上面板外壁面的投影处,因此,冷却液与上面板之间的换热为影响沿该路径温度变化的主要因素。从图10(a)可看出,除去入口端和出口端,局部温度最小值出现的位置均紧随皱褶偏折位置,而局部温度最大值均出现在每半个胞元的中后方位置。在每半个胞元中,温度呈现出先上升、后下降的趋势。这是由于上游冷却液越过波峰达到流速最大,该处对流换热最强,所以对应出现温度局部最小值,而后在一侧产生回流,另一侧遇到壁面先减速再不断加速,从而导致温度先升后降。
图11为在冷却液流动方向不同位置沿向的温度分布情况。其中各路径所在位置参见图3。由图11可知,冷却液温度沿向有着显著的变化,靠近上面板(热流输入侧)的位置温度很高,温度梯度很大,而中心区域温度较低,这是由传热过程决定的,同时也表明处在流道中央区域的冷却液利用率较低。另外,可以发现在靠近下面板区域的冷却液温度要高于中心区域的温度,这是由于固体结构的导热能力更强,一部分热量通过固体芯材侧壁向下传导至下面板,再由下面板与冷却液之间进行换热造成的。同时,从图11也可看出,冷却液温度沿流动方向不断升高。

图11 流体温度沿横向分布
4.3 不同雷诺数对结构换热性能的影响
针对V型皱褶芯材夹层结构,以芯材高度为特征长度定义以下量纲为1的参数:

。 (13)
式中:为冷却液入口流速;和f分别为冷却液的密度、黏度和热传导系数;为结构的平均换热系数。
设置一系列不同的入口速度值,并保持其他参数设置不变,分别进行求解。对于整个夹层板结构,不同流速下对应的雷诺数与平均努塞尔数之间的关系如图12所示,随着雷诺数的增加,结构平均努塞尔数也不断增大。强迫对流换热中,结构的平均努塞尔数可表示为雷诺数和普朗特数的函数,这里假设流体的普朗特数为常数,则平均努塞尔数与雷诺数之间的关系可拟合为

4.4 V型皱褶芯材与波纹芯材夹层结构热效率对比
通过上述分析可知,V型皱褶芯材夹层结构由于芯材的皱褶使换热得到增强。然而,曲折流道必然会导致比平直流道更高的压力损失,因此有必要对结构的综合热效率进行评估。为了便于比较,取与上述V型皱褶芯材夹层结构具有相同相对密度的波纹芯材夹层板的1个周期(如图13所示)进行研究。

图13 波纹芯材夹层板周期模型示意
针对本文研究对象,泵功率可表示为
≈Δ·20。 (15)
将平均对流换热系数表示为

式中:Δ为进口和出口间的压力损失;为总热流;为热流输入侧面板的面积,=20´(为了减少表达所涉及的参数,对于本文所讨论的对象,宽即2,长即5×2),根据式(13)、(15)和(16),采用文献[16]中定义的指标来表征结构的综合热效率,可得
。 (17)
其中,f和10/2分别体现了流体属性和外结构几何尺寸的影响,令
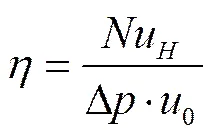
具有热流密度倒数的量纲,其综合考虑了结构的换热性能及对驱动冷却液流动的循环动力的要求。
2种结构的对比结果如表 3所示。从中可以发现,与波纹芯材夹层板相比,在相同入口速度下,V型皱褶芯材具有较高的换热性能,但同时需要更大的压力差来维持冷却液的流动;在相同压力差情况下,波纹芯材夹层板的努塞尔数更高,但表征结构综合热效率的值要比V型皱褶夹层板小。可见,在动力允许的条件下,V型皱褶芯材夹层结构换热性能更优,若对其皱褶几何参数进行优化,综合热效率有望进一步得到提高。

表 3 V型皱褶芯材与波纹芯材夹层结构热效率对比
4.5 V型皱褶芯材夹层结构热应力
V型皱褶芯材夹层板在上述温度场下结构应力与位移云图如图14所示。由应力云图(图14(a))可知,由于上面板温度较高,所以总体来说上面板应力水平较高,且在结构偏折位置均存在应力集中现象,其中最严重的部位发生在端部约束处,但尚未超出材料应力的许用值。对于高超声速飞行器而言,尤为关注在热载荷作用下的结构变形,因为较大的法向位移可能会破坏气动外形,从而导致更严重的气动加热。由位移云图(图14(b))可知,由于出口端约束较弱,且沿方向结构温度不断升高,所以沿方向变形不断变大。在夹层板厚度方向上,靠近热源输入侧的结构温度变化较大,因此上面板变形也较大,导致结构发生沿厚度方向的翘曲。向最大位移发生在结构中后部位置(见图14(c))。

(a) 应力云图
(b) 总位移云图

(c) z向位移云图
5 结论
本文采用数值计算方法,对强迫对流冷却条件下V型皱褶芯材夹层结构的传热性能及热-结构耦合问题进行了研究,得到以下结论:
1)在强迫对流条件下,冷却液与固体结构的对流换热降低了结构的温度,有效提高了皱褶结构承受热载荷的能力,有利于实现其承载和散热的多功能设计。
2)结构的皱褶构型导致冷却液速度场发生周期性的变化,在皱褶位置对流换热得到增强;沿流动方向,结构与冷却液的温度在逐渐升高的同时伴随有周期性的波动;结构的整体换热能力随着冷却液流速的增大而增强;与波纹芯材夹层结构相比,V型皱褶结构具有更优异的换热性能,但同时会带来较大的压力损失,在设计过程中对皱褶结构几何参数进行优化,可进一步提高其效率。
3)结构中的上面板热应力较大,由于几何形状的突变,在结构皱褶部位出现了热应力集中,最大应力发生在端部约束位置,最大法向位移发生在中后部位置。
作为潜在的承载/散热多功能结构,后续可综合考虑驱动冷却液所需的泵功率,结构的温度、应力、变形及屈曲等因素,对V型皱褶芯材夹层结构进行优化设计。
[1] 王志瑾, KHALIULIN V, SKRIPKIN E. 皱褶结构芯格构型的几何设计方法[J]. 南京航空航天大学学报, 2002, 34(1): 6-11
WANG Z J, KHALIULIN V, SKRIPKIN E. Geometry design method of folded structure[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2002, 34(1): 6-11
[2] LEBÉE A, SAB K. Homogenization of thick periodic plates: application of the bending-gradient plate theory to a folded core sandwich panel[J]. International Journal of Solids and Structures, 2012, 49(19/20): 2778-2792
[3] ELSAYED E A, BASILY B B. Applications of folding flat sheets of materials into 3-d intricate engineering designs: Working paper 07-015[R]. Rutgers University, 2009
[4] 蔡克乾, 靳明山, 姜开宇. 新型折叠夹芯结构材料研究进展[J]. 材料导报, 2015, 29(4): 129-133
CAI K Q, JIN M S, JIANG K Y. Review of progress in materials for sandwich structure with folded core[J]. Materials Review, 2015, 29(4): 129-133
[5] ZHAO D, LI Y, WANG M, et al. Fabrication of polymer origami-based V-type folded core[C]//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference: Volume 5B: 39thMechanisms and Robotics Conference. Boston, Massachusetts, USA, 2015
[6] 王志瑾, 徐庆华. V-型皱褶夹芯板与隔声性能实验[J]. 振动工程学报, 2006, 19(1): 65-69
WANG Z J, XU Q H. Experimental research on soundproof characteristic for the sandwich plates with folded core[J]. Journal of Vibration Engineering, 2006, 19(1): 65-69
[7] 王志瑾, 张辉, 徐庆华. 铝合金皱褶芯材夹层板当量导热系数[J]. 南京航空航天大学学报, 2008, 40(4): 507-512
WANG Z J, ZHANG H, XU Q H. Equivalent thermal conductivity coefficient for sandwich plates with folded core[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2008, 40(4): 507-512
[8] 周晨, 王志瑾, 支骄杨. 主动冷却皱褶芯材夹层板的热力分析[J]. 固体火箭技术, 2014, 37(4): 545-550
ZHOU C, WANG Z J, ZHI J Y. Thermal-mechanical analysis of actively cooled folded core sandwich panels[J]. Journal of Solid Rocket Technology, 2014, 37(4): 545-550
[9] 周华志, 王志瑾. M-型皱褶芯材夹层板吸能性能
研究[J]. 航空学报, 2016, 37(2): 579-587
ZHOU H Z, WANG Z J. Analysis of energy absorption capability of M-type folded core sandwich structure[J]. Acta Aeronautica ET Astronautica Sinica, 2016, 37(2): 579-587
[10] 张延昌, 王自力, 张世联. 折叠式夹芯层结构耐撞性能研究[J]. 船舶力学, 2010, 14(1/2): 114-120
ZHANG Y C, WANG Z L, ZHANG S L. Simulation analysis of folded core structure under dynamic load[J]. Journal of Ship Mechanics, 2010, 14(1/2): 114-120
[11] HEIMBS S. Foldcore sandwich structures and their impact behaviour: an overview[Z]. Dordrecht: Springer Netherlands, 2013: 491-544
[12] FISCHER S. Aluminum foldcores for sandwich structure application: mechanical properties and FE-simulation[J]. Thin-Walled Structures, 2015, 90: 31-41
[13] GRZESCHIK M. Performance of foldcores mechanical properties and testing[C]// International Design Engineering
Technical Conferences and Computers and Information in Engineering Conference: Volume 6B: 37thMechanisms and Robotics Conference. Portland, Oregon, USA, 2013
[14] 孙雨果, 高亮. 复合材料点阵夹芯结构的换热特性[J]. 复合材料学报, 2011, 28(4): 185-195
SUN Y G, GAO L. Heat transfer characteristics of composite sandwich structure with lattice cores[J]. Acta Materiae Compositae Sinica, 2011, 28(4): 185-195
[15] GAO L, SUN Y G. Thermal control of composite sandwich structure with lattice truss cores[J]. Journal of Thermophysics and Heat Transfer, 2015, 29(1): 47-54
[16] GAO L, SUN Y G. Fluid flow and heat transfer characteristics of composite lattice core sandwich structures[J]. Journal of Thermophysics and Heat Transfer, 2014, 28(2): 258-269
[17] 高亮, 孙雨果, 丛立新. 杆件倾角对复合点阵夹芯结构主动换热性能的影响[J]. 复合材料学报, 2013, 30(5): 180-186
GAO L, SUN Y G, CONG L X. Effect of inclination angle on active cooling performance of composite sandwich structure with lattice truss cores[J]. Acta Materiae Compositae Sinica, 2013, 30(5): 180-186
[18] RAKOW J F, WAAS A M. Response of actively cooled metal foam sandwich panels exposed to thermal loading[J]. AIAA Journal, 2007, 45(2): 329-336
[19] FENG S S, KUANG J J, WEN T, et al. An experimental and numerical study of finned metal foam heat sinks under impinging air jet cooling[J]. International Journal of Heat and Mass Transfer, 2014, 77: 1063-1074
[20] FENG S S, KUANG J J, LU T J, et al. Heat transfer and pressure drop characteristics of finned metal foam heat sinks under uniform impinging flow[J]. Journal of Electronic Packaging, 2015, 137(2): 21014
[21] 王储, 王建华, 杜治能, 等. 冷却介质在层板内流动特性研究: 第二部分数值模拟复杂结构内流场[J]. 实验流体力学, 2007, 21(4): 22-26
WANG C, WANG J H, DU Z N, et al. An investigation of coolant flow performance within laminated plate: II - numerical simulation of flow field of complex structure[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(4): 22-26
[22] HEIMBS S. Virtual testing of sandwich core structures using dynamic finite element simulations[J]. Computational Materials Science, 2009, 45(2): 205-216
[23] WILLIAMS S D, CURRY D M. Thermal protection materials: thermophysical property data[R]. NASA, 1992
[24] ANDERSON J D. 计算流体力学基础及其应用[M].北京: 机械工业出版社, 2007: 24-65
[25] BAPANAPALLI S K, MARTINEZ O M, GOGU C, et al. Analysis and design of corrugated-core sandwich panels for thermal protection systems of space vehicles[C]//47thAIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Newport, Rhode Island, 2006
[26] 范绪箕. 高速飞行器热结构分析与应用[M]. 北京: 国防工业出版社, 2009: 39-62
[27] 张靖周, 常海萍. 传热学[M]. 北京: 科学出版社, 2015: 258-265
(编辑:张艳艳)
Heat transfer and thermal stress analyses of V-pattern folded core sandwich structures subjected to forced convection
ZHOU Chen1, WANG Zhijin1, HOU Tianjiao2
(1. Minister Key Discipline Laboratory of Advanced Design Technology of Aircraft, Nanjing University of Aeronautics and Astronautics; 2. College of Aeronautics, Nanjing University of Aeronautics and Astronautics: Nanjing 210016, China)
The combination of the V-pattern folded cores and the forced convection may apply to the multi-functional design the simultaneous load bearing and the heat dissipation for hypersonic vehicles or high-power electronic devices. The heat transfer and thermal stress characteristics of a V-pattern folded core sandwich panel subjected to the forced convection are investigated numerically to obtain the velocity field, the temperature field, and the structural thermal stress distribution. It is shown that the heat transfer performance of the V-pattern folded panels is evidently improved under the forced convection, however, an elevated pressure drop is also observed. The coolant velocity varies periodically with the geometrical construction and reaches the maximum value close to the peak position of the buckling, where the heat convection is therefore reinforced. The temperature increases along the flow direction and sees a periodic fluctuation. The overall heat transfer performance is refined with the increase of the inlet velocity. The thermal stress as well as the deformation are comparatively large in the face sheet near the heat source and the stress concentration is found at the folding positions.
folded core; forced convection; sandwich structure; heat transfer characteristics; thermal stress
V414.9
A
1673-1379(2017)04-0355-09
10.3969/j.issn.1673-1379.2017.04.003
周晨(1989—),男,博士研究生,主要研究方向为飞行器设计和热防护结构设计;E-mail: zhouchen@nuaa. edu.cn。指导教师:王志瑾(1963—),女,教授,博士生导师,主要从事飞行器结构设计、结构优化设计和热防护结构设计等研究;E-mail: zhijin@nuaa.edu.cn。
2017-02-24;
2017-07-11
中央高校基本科研业务费专项资金资助项目(编号:NZ2016101);江苏省普通高校研究生科研创新计划资助项目(编号:CXLX13_163);江苏高校优势学科建设工程资助项目

