航天器在轨释放安全性分析与仿真研究
范高洁,柏林厚,魏传锋,巩朝阳
航天器在轨释放安全性分析与仿真研究
范高洁,柏林厚,魏传锋,巩朝阳
(中国空间技术研究院载人航天总体部,北京100094)
针对航天器舱内在轨释放任务,文章建立了大型航天器与伴随卫星的动力学模型和运动学模型,并分析了影响释放安全性的主要因素;从保证航天器在轨安全的角度,得到描述释放安全性的最小相对距离计算方法,并利用ADAMS软件对航天器在轨释放过程进行了仿真研究。
在轨释放;安全性分析建模;ADAMS仿真
0 引言
航天器在轨释放是指大型航天器在飞行过程中利用舱外或舱内分离机构释放小型独立飞行器(又称为伴随卫星)的过程。在轨释放过程中,由分离机构给伴随卫星提供足够的分离力,以使伴随卫星获得初始的相对速度,并以固定姿态与大型航天器分离。
航天器在轨释放过程中,可能产生碰撞风险,若是载人航天器还会影响到航天员的安全。由于分离力属于两航天器之间的内力,施加后对它们的质心位置和姿态都会产生影响。若伴随卫星安装在大型航天器壳体外部,分离释放的安全性主要考察两航天器相对质心位置的变化情况[1],以及在近距离时伴随卫星的姿态偏差;若在壳体内部,则意味着伴随卫星分离时还需要在器内运动一段距离,该距离可以看作是“释放通道”。伴随卫星在释放通道内运动时对安全性影响较大的是伴随卫星的运动方向偏差以及姿态变化偏差,离开释放通道后影响航天器安全的主要是伴随卫星质心相对于大型航天器的距离。
伴随卫星和大型航天器之间的最小距离是释放安全性分析的重要评价指标。影响最小距离的误差源很多,主要分析各误差项对于伴随卫星姿态以及释放方向的影响,再采用单一误差和综合误差的分析方法,确定伴随卫星的最大姿态偏差,并在考虑一定余量的情况下最终确定大型航天器释放通道的设计状态。
在在轨释放仿真分析领域,舒燕等[2]主要研究了在轨释放和分离载荷的动力学特点,即针对偏离于多体几何中心的释放分离载荷以及基于质量特性变化的多体动力学问题,利用ADAMS软件分析了各种释放方案对载荷的冲击影响。王功波等[3]利用Hill方程推导了分离速度的解析表达式,指出大气阻力和沿轴方向释放速度是影响最小距离的主要因素,并给出了基于分离速度的最小距离解析表达式。
本文建立了大型航天器与伴随卫星在轨释放的姿态动力学模型,针对“舱内释放”工况,分析释放过程中分离力偏差与力矩偏差的主要来源;在考虑这些偏差的基础上对模型进行了修正,得到了基于最小距离的安全性分析模型;最后利用航天器的ADAMS模型进行了算例仿真,分析了不同偏差因素对释放安全性的影响。
1 姿态动力学模型
设大型航天器A受到释放分离力作用,产生的姿态角速度为A,分离力作用点至大型航天器质心的距离矢量为A,产生的力矩和动量矩为A和A,根据相关定义[4],则有

考虑到
, (2)
则可得到

。(4)
综上各式,最终可得到

即
。 (6)
实际任务分析中,一般选取大型航天器设计坐标系作为表述姿态与计算惯量矩阵的坐标系,故惯量矩阵可看作一个常数矩阵。动量矩在航天器设计坐标系下的导数为

伴随卫星分离力对航天器质心产生的力矩为
。 (8)
根据动量矩定理,则有

综上所述,最后得到
。 (10)
另外,通过“3-1-3”变换方式[5]进行矩阵转序,得到航天器姿态运动学方程为

也可写成
。(12)
最后得到转序矩阵A为

同理,可推导出伴随卫星B的动力学与运动学方程有
; (14)

相关的转序矩阵B为
。 (16)
2 释放分离力模型
一般来说,由伴随卫星释放机构中的分离推杆或弹簧提供分离的初始相对速度,而分离导向装置起到限制运动方向的作用。因此分离力可表示为

式中:为黏滞阻尼系数;为弹簧刚性系数;为弹簧两端的相对位移;0为弹簧两端的初始相对位移;d/d为弹簧两端的相对速度;0为弹簧的预紧作用力。
从伴随卫星的释放过程来看,导致出现姿态偏差的主要因素有:两航天器的质量特性偏差,分离执行机构安装偏差,分离推力偏差,分离机构的残余冲量等。下面将逐一进行分析。
1)质量特性偏差
根据式(10)可知,质心位置和转动惯量会影响航天器分离时的相对姿态,故在设计时需考虑两航天器的质量特性偏差,由此分别计算伴随卫星释放过程中运动方向以及两航天器的相对姿态运动。
假设质心位置相对于标称质心位置的偏差为zl,转动惯量偏差为zl,则质量特性偏差产生的干扰力为
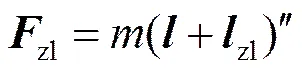
干扰力矩为
; (19)
干扰角动量为

2)分离执行机构安装偏差
分离执行机构主要指分离推杆或弹簧,其安装偏差将导致分离力作用点的偏差。
假设分离力作用点偏差为az,则安装偏差产生的干扰力为

干扰力矩为
; (22)
干扰角动量为

在研究相对姿态运动时,主要考察伴随卫星的姿态相对于其质心的变化情况,因此在工程中将分离执行机构安装偏差等效为伴随卫星的质心位置偏差进行分析,以考察其对释放过程中两航天器间最小距离的影响。
3)分离推力偏差
分离执行机构一般采用多重冗余的设计,即由多个执行机构共同提供伴随卫星的分离力。理想情况下各执行机构的分离力应是相等的,以保证伴随卫星的受力方向与释放方向一致。当不同分离执行机构产生的分离推力大小有偏差时,分离力的合力大小与力作用线方向都会发生变化。假设个分离执行机构产生的推力分别为1,2, …,,(=1, 2, …,),产生的合力为

对伴随卫星产生的干扰力矩为
; (25)
对伴随卫星产生的干扰角动量为

4)分离机构残余冲量不均衡性
在实际的释放机构中,分离力的来源主要包括分离弹簧作用或火工品引爆后产生的瞬时冲量。若分离力不均衡地作用在伴随卫星上,则会引起伴随卫星的姿态扰动。
设分离机构中安装个分离螺母,引爆后产生的残余冲量分别为
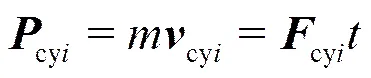
多个分离螺母的残余冲量差为
(=1, 2, …,)。 (28)
工程应用中,平均残余冲量以及残余冲量差一般作为分离释放机构的设计指标给出,据此可计算出由冲量引起的等效分离推力或等效分离速度,最终得到由残余冲量的不均衡性引起的姿态偏差。
3 释放安全性分析模型
考虑释放过程的安全性,需要重点关注以下3个方面:
1)分离推力需保证伴随卫星释放后与航天器的相对轨道满足安全轨迹要求,或一定时间到达的相对距离满足轨道安全性要求。
2)伴随卫星在释放通道运动过程中,分离推力方向偏差需保证卫星不会撞击到释放通道内结构;
3)伴随卫星在释放通道运动过程中,分离推力对伴随卫星产生的姿态干扰力矩需保证卫星不会撞击到航天器。
针对上述3个方面,伴随卫星的释放安全性分析步骤为:
1)根据分离弹簧性能参数以及由此提供的标称分离力,计算出标称分离速度;
2)结合以上引起推力大小及方向偏差的影响因素,逐个分析它们所引起的伴随卫星推力方向偏差和释放姿态偏差;
3)根据释放通道设计技术状态,计算在偏差工况下伴随卫星与航天器之间的最小距离,判断是否满足释放安全性要求,若距离较小,则需要提出改进措施。
可以根据安装的静态分析,找出伴随卫星在释放通道中距离航天器壳体最近的点1(在伴随卫星上),对应的航天器上距离伴随卫星最近的点2(在航天器上),最近距离出现的时刻为j,安装静态下最近距离为0。
假设在释放过程中,大型航天器受到分离推力影响,1点产生的相对位移为D1;伴随卫星受到分离推力影响,2点产生的相对位移为D2,则实际释放过程中两航天器的最近相对距离为

下面分别求解Dd1和Dd2。假设释放机构解锁后到伴随卫星离开释放通道期间,P1点移动到P1′,如图1所示。
在航天器设计坐标系下,根据式(13)可知,1点的位移与姿态角变化的关系为

故有
, (31)
受到分离推力影响,伴随卫星会产生质心的平动以及绕质心的转动,假设质心点移动到¢点,2点移动到2,如图2所示。

图2 释放过程中伴随卫星B的姿态变化
从¢点作矢量平行于,在航天器设计坐标系下,则有

式中B为伴随卫星姿态转序矩阵,见式(16)。为质心平动位移量,即记为,可通过对
(33)

求出。
最终可求解出在实际分离推力影响下伴随卫星在释放通道内与航天器的最小安全距离。
另外,还可根据最小安全距离反算得到现有释放通道能够容忍的伴随卫星最大姿态偏差,如图3所示。

图3 伴随卫星姿态偏差示意图
由几何关系可得

即释放通道能够容忍的伴随卫星的单个姿态偏差最大不能超过,否则会与航天器发生碰撞。
4 基于ADAMS模型的释放安全性仿真
作为算例,建立卫星在轨释放ADAMS模型,如图4所示。

航天器和伴随卫星的质量特性参数如下:
1)航天器A
质量A=2500kg;质心位置A=(1100,5,2)mm;转动惯量A=kg·m2。
2)航天器B
质量B=30kg;质心位置B=(0,0,160)mm;转动惯量B=kg·m2。
两航天器之间设置2个弹簧,每个弹簧产生176N分离力。设置在仿真开始第0s时释放伴随卫星,仿真时间2s,得到标称情况下两航天器之间最小距离的变化情况如图5所示,最小距离为38.1cm。

图5 在轨释放期间航天器间最小距离变化
在仿真过程中,根据工程研制经验以及地面试验测量数据,伴随卫星的质量特性偏差取为5%、3轴安装偏差皆为±0.2°、分离螺母的残余冲量为0.2N×s、弹簧推力偏差和导向偏差分别为5%和0.2°,仿真结果见表1。

表1 考虑多种影响因素的仿真结果
由于两航天器质量特性相差较大,在轨释放过程中对释放安全性影响较大的因素是弹簧推力偏差,伴随卫星的质量特性偏差、安装方向偏差以及整器的质量特性偏差对最小距离影响较小。
据此,又对推力偏差、释放方向偏差和质量特性偏差3种因素进行了综合偏差分析,并且对比了不同因素的影响,综合仿真分析结果分别见表2。

表2 综合仿真分析的结果
根据仿真计算的结果,可得到以下几点结论:
1)各仿真工况下大型航天器的姿态变化较稳定,受各种伴随卫星偏差影响较小。
2)由表2可以看出,推力偏差主要影响着伴随卫星偏航方向角速度;质量特性偏差主要影响伴随卫星滚动方向角速度;释放方向偏差主要影响偏航方向与俯仰方向角速度。
3)综合来看,表2中工况12最为严酷,在该工况下仿真得到的伴随卫星与大型航天器的最小距离仅为10.6mm,因此在实际工程任务中需采取手段避免该工况条件的出现。
5 结束语
本文通过建立航天器在轨释放姿态动力学模型,针对舱内释放方式,建立基于最小距离的安全性分析模型,并利用航天器的ADAMS模型进行了算例仿真分析。该方法在工程上易于实现,可以较快地进行在轨释放安全性设计与复核,将为我国后续小卫星在轨释放提供一定参考。
[1] 吴会英, 陈宏宇, 周美江, 等. 伴随卫星轨控时机与相对运动椭圆大小控制效率的关系[J]. 载人航天, 2013, 19(5): 90-96
WU H Y, CHEN H Y, ZHOU M J, et al. Research on relationship between orbit control time and control efficiency of concomitant satellites[J]. Manned Spaceflight, 2013, 19(5): 90-96
[2] 舒燕, 李志. 在轨释放、分离载荷动力学仿真研究[J]. 航天器环境工程, 2012, 29(1): 18-22
SHU Y, LI Z. Dynamics simulation of on-orbit release and separation of payload[J]. Spacecraft Environment Engineering, 2012, 29(1): 18-22
[3] 王功波, 郗晓宁. 小卫星在轨安全分离速度设计[J]. 中国空间科学技术, 2007(3): 33-38
WANG G B, XI X N. Safety on-orbit releasing velocity design for small satellites[J]. Chinese Space Science and Technology, 2007(3): 33-38
[4] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1999: 149-155
[5] 周军. 航天器控制原理[M]. 西安: 西北工业大学出版社, 2001: 45-47
(编辑:肖福根)
Safety analysis and simulation of spacecraft on-orbit releasing
FAN Gaojie, BO Linhou, WEI Chuanfeng, GONG Chaoyang
(Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China)
For the mission of spacecraft on-orbit releasing, dynamic and kinematic models are established for both the main spacecraft and the concomitant satellite in this paper. By analyzing the main force model that affects the releasing safety during the process, the closest distance between two spacecrafts can be calculated, under the condition of assuring the on-orbit safety of two spacecrafts. The software ADAMS is used for simulating the releasing process.
on-orbit releasing; safety analysis and modeling; ADAMS simulation
V411.8
A
1673-1379-2017(04)-0403-07
10.3969/j.issn.1673-1379.2017.04.011
范高洁(1986—),女,硕士学位,从事载人航天器总体设计与轨道设计工作。E-mail: ceciliagj@126.com。
2017-05-30;
2017-06-11

