Distributed fixed-time attitude coordinated control for multiple spacecraft with actuator saturation

Han GAO, Yuanqing XIA, Xiaopu ZHANG, Guangchen ZHANG

School of Automation, Beijing Institute of Technology, Beijing 100081, China

KEYWORDS Multiple spacecraft;Distributed attitude control;Fixed-time observer;Fixed-time controller;Actuator saturation

Abstract This paper investigates the distributed fixed-time attitude coordinated control problem for multiple spacecraft subject to actuator saturation under the directed topology. First, a distributed fixed-time observer is presented for each follower spacecraft to estimate the leader spacecraft’s states. Compared with the commonly used fixed-time observer, the settling time of the proposed fixed-time observer can be easily adjusted by some free design parameters. Next, a distributed fixed-time control scheme is derived by using the estimates of the leader spacecraft’s states and the adding a power integrator technique. When considering actuator saturation, an auxiliary system is utilized to compensate the saturation. Further, a rigorous theoretical proof is provided to show that the practical fixed-time stability of the closed-loop system is ensured. Finally, simulation results illustrate the benefits and effectiveness of the developed control scheme.

1. Introduction

Spacecraft Formation Flying (SFF) has attracted increasing attention recently.Unlike the existing large spacecraft, a group of micro spacecraft has higher flexibility, reliability,and lower cost. Therefore, the SFF has broad potential applications for a variety of complex space missions, such as distributed aperture radar, earth observation stereo-imaging,and deep space exploration.So far, several distributed attitude coordinated control laws have been applied for SFF,including backstepping controller,observer based controller,adaptive controller,and sliding mode controller.

However, it is worth noticing that the previously listed distributed attitude control laws achieve attitude asymptotic stability of the closed-loop system,which means that the attitude synchronization is achieved asymptotically with infinite settling time and is very hard to implement in practice. In order to solve this problem, finite-time control, which can provide a faster convergence rate, becomes an alternative way for attitude coordinated control for SFF. In the past few years,numerous results of finite-time attitude coordinated control have been achieved based on the terminal sliding mode method,the adding a power integrator technique,and the homogeneity theorem.

Although the finite-time control offers faster convergence than the asymptotic control, the settling time of the finitetime control is dependent not only on the control parameters but also on the initial states of the system. Due to this drawback, the upper bound of the convergence time is very hard to be determined when the initial states are unknown in advance. Compared with the finite-time control, the convergence time of the fixed-time control is independent of the initial states. Because of this advantage, the fixed-time control has received widespread attention. For instance, a fixed-time controller was proposed to ensure the spacecraft attitude to have fixed-time convergence in Ref. 17. In Ref. 18, the fixed-time attitude stabilization problem for the flexible spacecraft was studied.In Ref.19,a fixed-time attitude tracking control problem for the rigid spacecraft with input quantization was developed. However, the aforementioned results on fixed time attitude control are designed for the single spacecraft. They cannot be directly applied to the attitude coordinated control for multiple spacecraft, as the information flow among the spacecraft in the formation must be taken into account. Very recently,some results are obtained on multiple spacecraft attitude control. By using the adding a power integrator technique, a distributed fixed-time attitude coordination controller was studied for multiple rigid spacecraft.In Refs.21,22, the sliding-mode estimator based fixed-time controller was developed for the distributed attitude synchronization control problem. Based on the investigations of Refs. 21,22,an output feedback fixed-time controller was proposed for multiple spacecraft system in Ref.23.However,it is worth noting that the bidirectional information exchange among different spacecraft is required in the aforementioned fixed-time attitude coordinated controllers, which means that these control strategies cannot be used under the directed topology condition.

Another practical problem encountered in the practical SFF is that the onboard actuators used for spacecraft attitude control are susceptible to suffer from magnitude constraints.If the actuators are saturated for a long time, the good performance of the control system cannot be reached or instability could even be resulted in Ref.24 Therefore,the actuator saturation is an unavoidable issue that should be considered.Some methods have already been presented to solve the actuator saturation issue in the existing literature.In Ref.25,a radial basis function neural network based feed-forward saturation compensator was derived to reduce the effect of the unknown control input saturation.In Ref.26,the bias between the designed control input and the saturated one was regarded as a bounded disturbance, and robust controller was designed. In Ref. 27,the smooth arc-tangent function was adopted to model the constrained control input, and an augmented plant was constructed. Although the actuator saturation problem has been extensively studied, very few fixed-time results were achieved in the existing literature for multiple spacecraft attitude control.

Motivated by the above discussion, we propose a novel fixed-time control scheme for multiple spacecraft attitude coordinated control system in the presence of actuator saturation under directed topology. The main achievements of the proposed control scheme are shown as follows:

(1) A fixed-time observer is designed to estimate the leader

spacecraft’s information for each follower spacecraft under directed topology. Unlike the existing fixed-time observers,in this paper, the free design parameters are introduced in the proposed fixed-time observer, by which the upper bound of the settling time of the proposed fixed-time observer can be easily adjusted.

(2) By utilizing the proposed fixed-time observer and the adding a power integrator technique, a distributed fixed-time attitude controller is established. In contrast to the existing asymptotic or finite-time controllers,the convergence time of the proposed controller is bounded by a constant independent of initial states.

(3) Compared with the existing fixed-time attitude coordinated controllers,the actuator saturation problem is solved by an auxiliary system in this paper.

(4) Compared with the existing fixed-time attitude coordinated control laws,the control strategy proposed in this paper can solve the multiple spacecraft fixedtime attitude coordinated problem under the directional communication topology.

The remainder of this paper is organized as follows.In Section 2,problem formulation and preliminary are presented.In Section 3 and Section 4,a fixed-time observer and an adaptive fixed-time controller are devised and analyzed strictly.Illustrative examples and analysis are presented to validate the effectiveness of the proposed control approach in Section 5.Section 6 draws some conclusions and presents future plans.

2. Problem formulation and preliminary

2.1. Notations

2.2. Spacecraft attitude dynamics and kinematics

In this paper, the attitude dynamics and kinematics of the ith(i=1，2，...，n) follower spacecraft using Modified Rodrigues Parameters (MRPs)are given as

2.3. Graph theory

2.4. Useful lemmas and assumptions

Consider the system in the following form:

Assumption 3 (). For the practical spacecraft attitude system described by Eq. (5) with input saturation and desired trajectory,a feasible commanded input uthat the specified tracking control objective can be achieved should exist.

Remark 2. Assumption 3 implies that the spacecraft attitude system (5) is controllable and the input difference Δu=T（u）-ubetween the saturation input T（u） and the commanded control input uis bounded,namely‖Δu‖≤uwith ubeing an unknown positive constant. For the view of a practical control system,Assumption 3 is reasonable.The commanded control input cannot be too large.If the commanded control input is too large,it indicates that the actuator cannot provide enough energy to make the practical system stable. Meanwhile, the upper bound of ‖Δu‖does not need to be known, which will only be used to analyze the stability of the closed-loop system later. In the recent literature,the similar assumption can be found.

2.5. Control objective

The control objective of this paper is to develop a distributed observer-based attitude controller for a group of rigid spacecraft, so that the states of the follower spacecraft subject to actuator saturation synchronize to those of the leader spacecraft in fixed time over a directed graph.

3. Fixed-time observer design

Since the states of the leader spacecraft are only available to a subset of the follower spacecraft, the fixed-time distributed observer is first designed for each follower spacecraft in the formation to obtain an estimation of the information of the leader spacecraft. Let x=σand x= ˙σbe the states of the leader spacecraft and denote ^xand ^xas the estimates of xand xfor the ith follower spacecraft. For the convenience of the fixed-time observer design, two variables are introduced.

Remark 3 (). Compared with the existing finite-time observers, the settling time of the fixed-time observer (10) is only related to the observer parameters.Therefore,it can be said that the fixed time Tcan be guaranteed in a prescribed manner.Meanwhile, it is worth noting that the fixed-time observer is proposed under the directed topology condition. It has lower communication cost than the one under the undirected topology.

4. Fixed-time controller design

Then, a recursive backstepping procedure is performed to develop the fixed-time attitude controller for each follower spacecraft as follows.

Step 1.

where h, h, and hare the control parameters.

The main result of this paper is stated in the following theorem.

Theorem 2. Consider a group of n spacecraft described by Eq.(5). Suppose Assumption 1-3 hold. If the fixed-time observer is designed as Eq. (10), the fixed-time attitude control law is given by Eq.(35),and the adaptive compensation law is chosen as Eq.(36). The control parameters satisfy

Summarizing the analysis in Cases 1 and 2, it can be concluded that there exists a T=T+Tso that the fixed-time tracking is achieved for each follower spacecraft.

The proof is completed. □

Remark 5. Compared with the existing results,no waiting time for observer convergence is required during the whole process. It means that the controller can be utilized at the beginning of the SSF mission. When 0 ＜t ＜T, the fixed-time observer (10) does not complete the observation, and the estimated states of leader spacecraft are tracked by the proposed controller (35) for each follower spacecraft. When t ≥T, the proposed fixed-time observer(10)makes an accurate estimate of the leader spacecraft and the command signals of the controller(35)become the actual states of the leader spacecraft.Therefore,the proposed control scheme can provide a faster response,which will be demonstrated in the next section by simulation.

Remark 7. It should be mentioned that the auxiliary system(36)is inspired by Ref.However, only asymptotic convergence result can be achieved in Ref.In contrast, we utilize the designed auxiliary system(36)to ensure the practical fixed-time stability of the closed-loop system under the actuator saturation.

5. Simulation

For verifying the effectiveness of the proposed control scheme,the numerical example is organized in this section. It is assumed that there are four follower spacecrafts with one leader spacecraft in the formation, of which the topology is illustrated in Fig. 1.

For four follower spacecrafts, the inertia matrices are

The observer parameters of the ith follower spacecraft are selected as c=0.1, c=0.1, ε=0.05, ε=0.05, l=0.02,l=0.015, α=0.9, and β=1.1. The controller parameters of the ith follower spacecraft are selected as p=0.1, p=1,δ=1.2, θ=0.8, k=10, k=10, k=0.5, k=0.003,h=1, h=1, and h=5. The max control torque is selected as 0.5N·m.

5.1. Verify the effectiveness of the proposed control scheme

For the given initial conditions, the observation errors of the proposed distributed fixed-time observer (10) are recorded in Fig. 2 and Fig. 3.

From Fig. 2 and Fig. 3, it can be seen that the proposed fixed-time observer (10)has a good estimate of σand ˙σwith a fast response. The observer errors converge to acceptable accuracy in 6 s. In other words, the states of leader spacecraft are effectively estimated by the proposed observer.

The time responses of the tracking errors xand xfor each follower spacecraft are given in Fig. 4 and Fig. 5. It can be observed that the states of all follower spacecraft reach on a common attitude even when only a subset of the group members can have access to the reference attitude over a directed topology in fixed time.The control torque of the proposed controller is recorded in Fig. 6. Obviously, the control torque is bounded by 0.5N·m throughout the process.

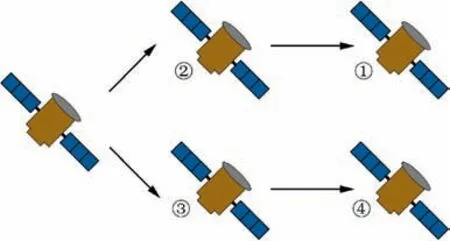
Fig. 1 Communication topology.

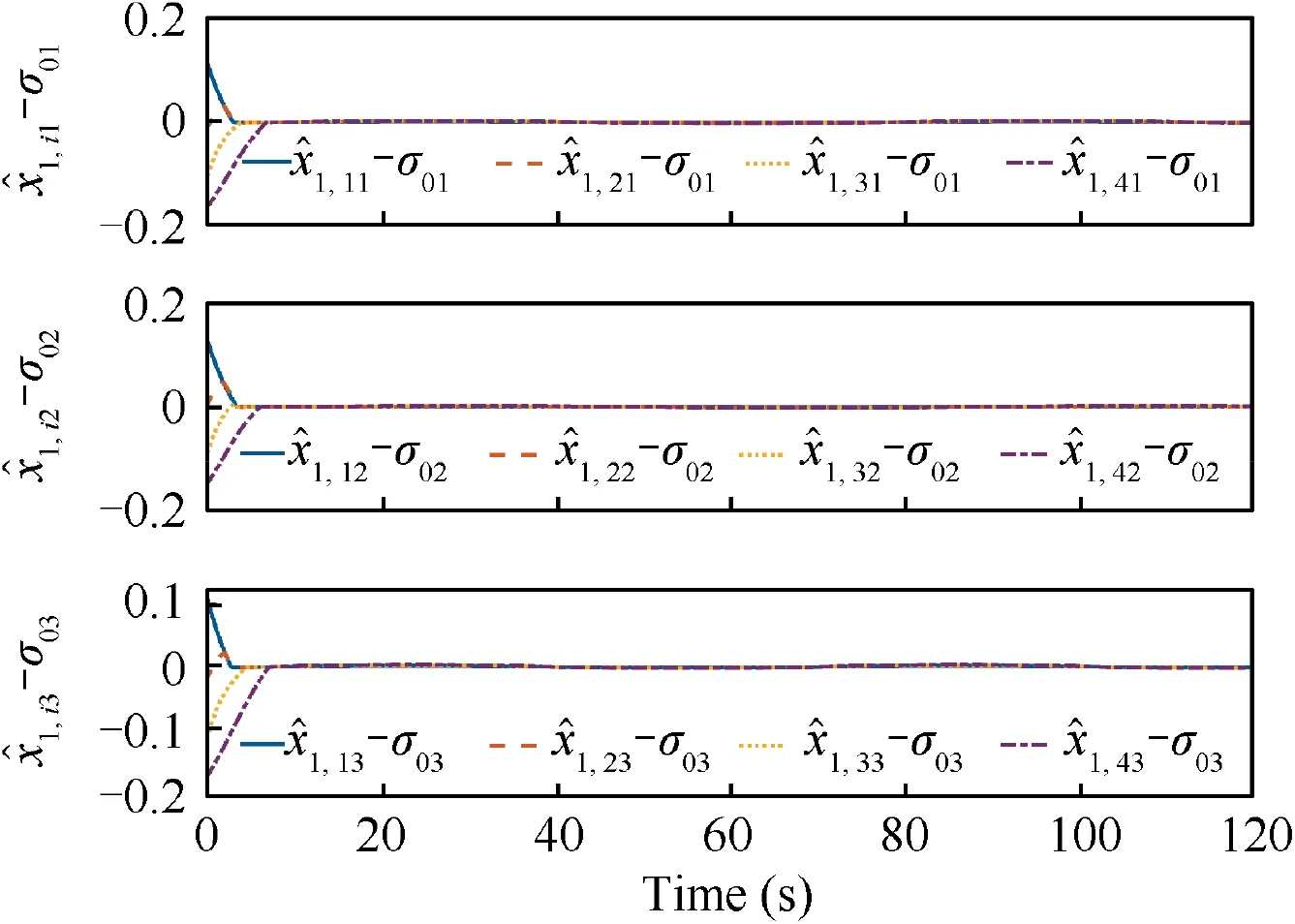
Fig. 2 Estimate errors -σ0 for the fixed-time observer (10).

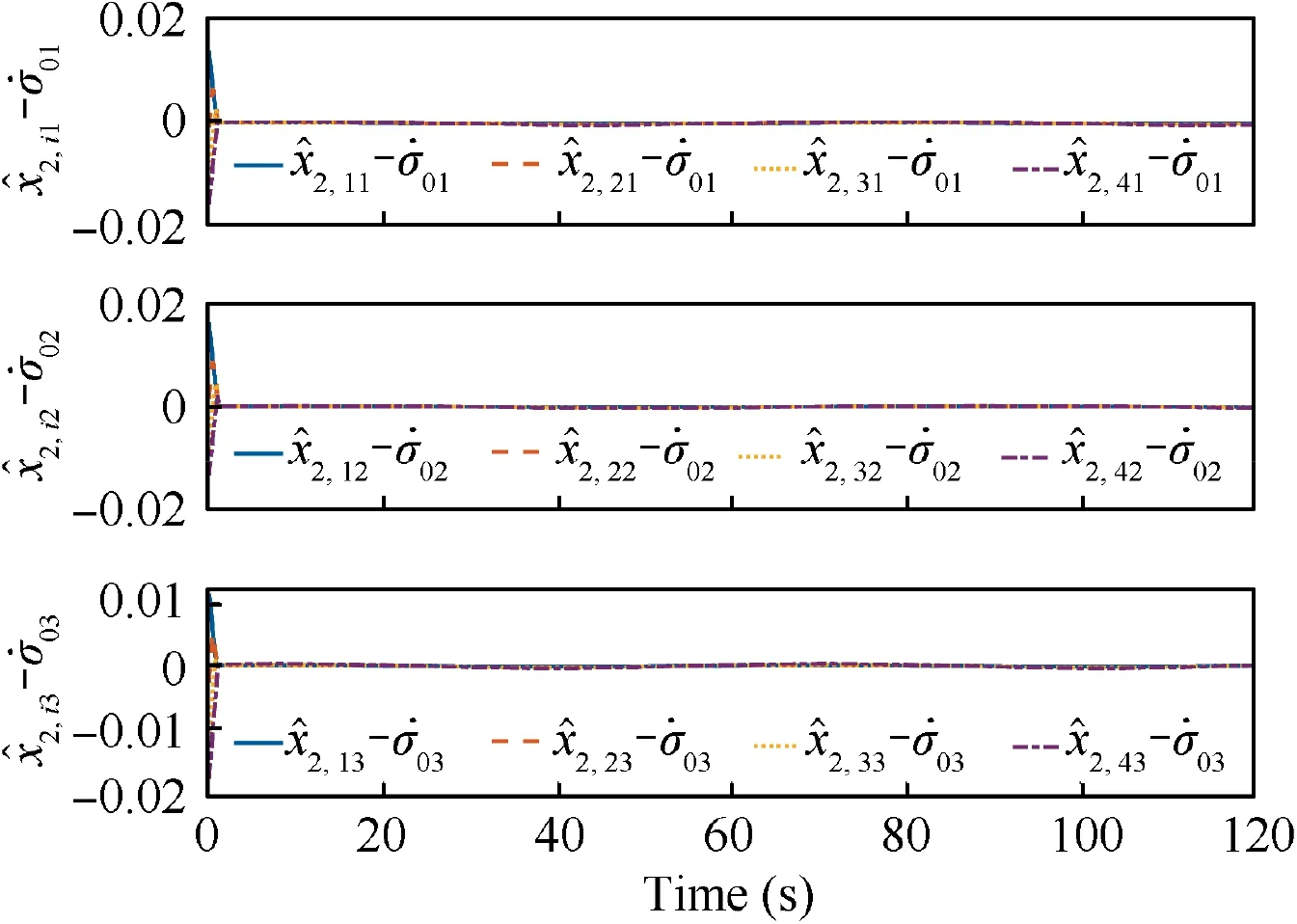
Fig. 3 Estimate errors i- for the fixed-time observer (10).

As described in Remark 5 in Section 4,an important advantage of the proposed control scheme is that the proposed fixedtime controller(35)works at the beginning of the SSF mission instead of waiting for ^x=xand ^x=xwhen t ≥T.For illustrating this superiority of the proposed control scheme, a comparison between different cases is carried out.In Case 1, the proposed fixed-time controller works after T.In Case 2, the proposed fixed-time controller works at the beginning.

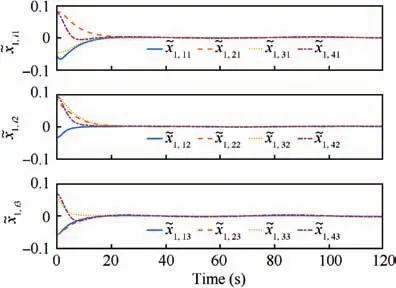
Fig. 4 Tracking errors of follower spacecraft.

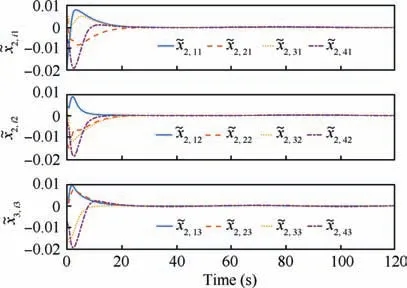
Fig. 5 Tracking errors of follower spacecraft.

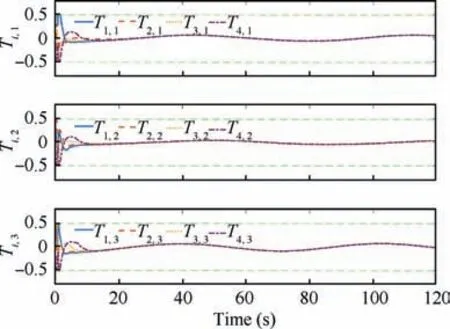
Fig. 6 Control torques Ti of follower spacecraft.

The response curves of SKAE and FKAE in different cases are recorded in Fig. 7 and Fig. 8 respectively. It is shown that the proposed control scheme, which is recorded in Case 1,achieves faster response performance with a settling time less than 23 s. One can obtain that the proposed control scheme manages to track the desired attitude at the beginning. However, the control scheme, which is recorded in Case 2, fails to stabilize the spacecraft attitude control system before T.

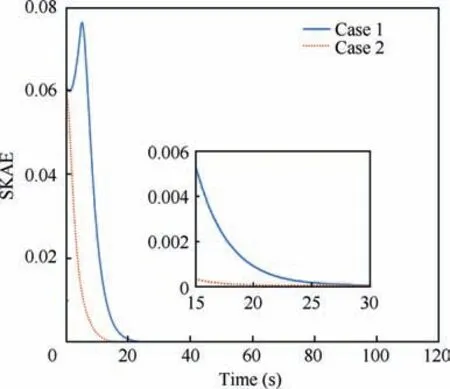
Fig. 7 SKAE in different cases.

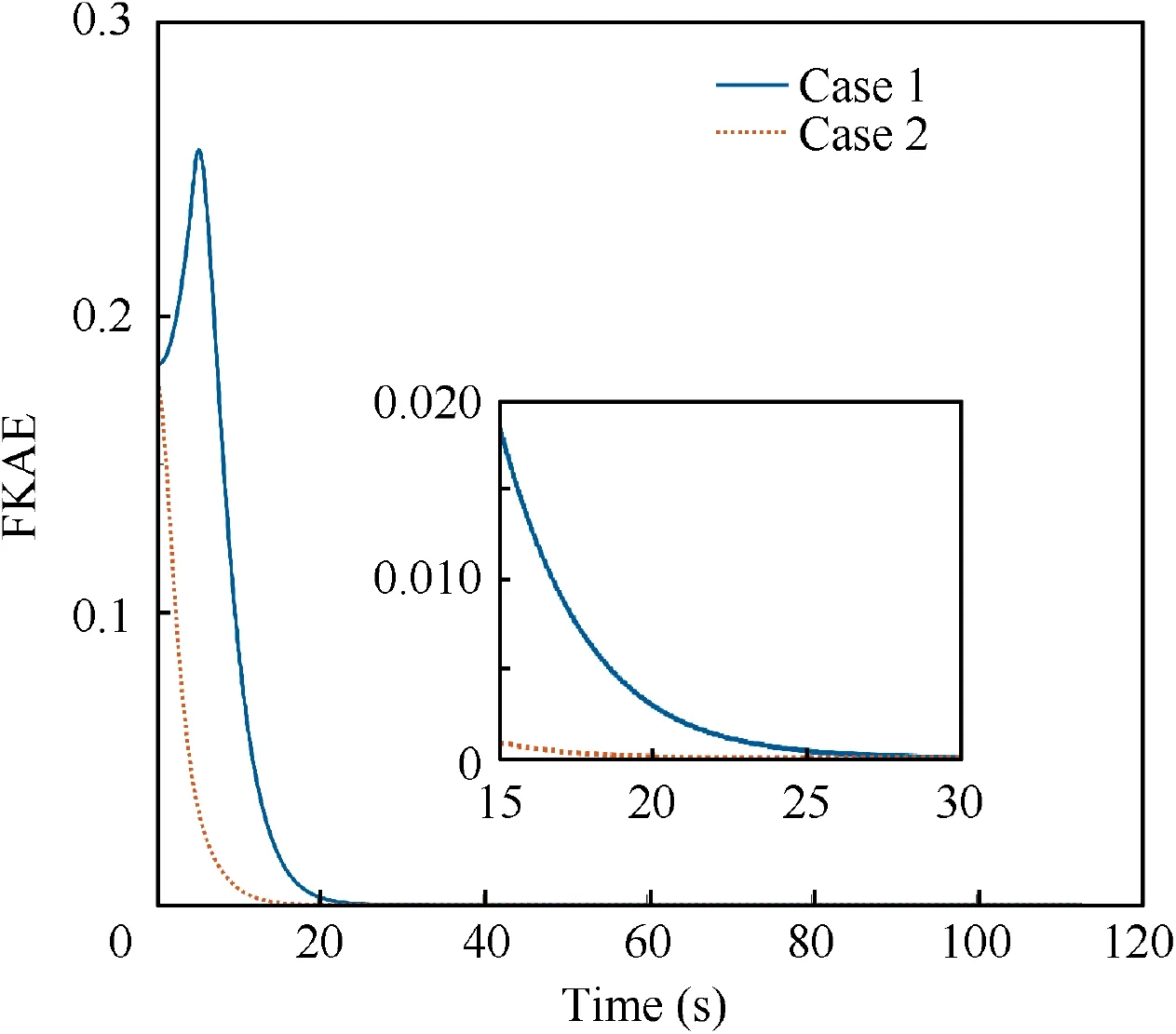
Fig. 8 FKAE in different cases.

5.2.Compare the control performance of the proposed controller with that of others

In order to validate and evaluate the performance of the proposed control scheme, the asymptotic controller (i.e., the control law (35) with δ=1 and θ=1) and the finite-time controller (i.e., the control law (35) with δ=0.8 and θ=0.8)are applied to the considered multiple spacecraft attitude system to carry out numerical simulation for the purpose of comparison.

With the same initial states, the response curves of SKAE and FKAE of different controllers are shown in Fig. 9 and Fig. 10 respectively. It can be seen that the proposed fixedtime controller exhibits a faster convergence rate than the other two controllers in both SKAE and FKAE.

To sum up, it can be concluded from the above simulation results that the presented fixed-time control approach successfully solves the fixed-time attitude coordinated control problem for multiple spacecraft with actuator saturation.

6. Conclusions

Fig. 9 SKAE comparison among the asymptotic, finite-time,and fixed-time control schemes.

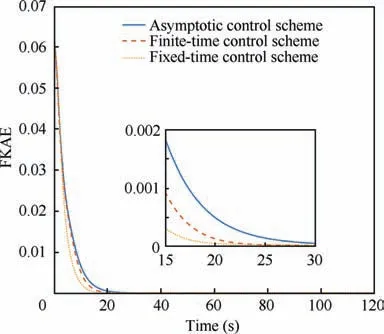
Fig. 10 FKAE comparison among the asymptotic, finite-time,and fixed-time control schemes.

A fixed-time attitude control scheme is proposed for the spacecraft formation system subject to actuator saturation.To solve the problem that the leader spacecraft’s states are available only to a subset of the group members, a fixed-time observer is designed,which can provide accurate observed states in fixed time. On the basis of the proposed observer, a distributed fixed-time attitude controller is developed.An auxiliary system is used to solve the issue of actuator saturation. Numerical simulation result and comparison have shown the advantages and improvements of the proposed control scheme. In our future work, the extension of the proposed control scheme to fault tolerant case will be investigated.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

s

This work was supported by the National Natural Science Foundation of China (Nos. 61720106010, 62003041), Science and Technology on Space Intelligent Control Laboratory,China (No. KGJZDSYS-2018-05), and General Project of Ningxia Natural Science Fund, China (No. 2020AAC03234).