Periodic acoustic source tracking using propagation delayed measurements

Huijuan HAO, Zhansheng DUAN

a Center for Information Engineering Science Research, Xi’an Jiaotong University, Xi’an, 710049, China

b School of Mathematics and Statistics, Ningxia University, Yinchuan, 750021, China

KEYWORDS Periodic acoustic source;Propagation delay;Target Motion Analysis(TMA);Cubature Kalman Filter(CKF);Gauss-Helmert model

Abstract There exist a large class of acoustic sources which have an underlying periodic phenomenon. Unlike the well-studied Bearings-Only Tracking (BOT) of an aperiodic acoustic source,this paper considers the problem of tracking a periodic acoustic source.For periodic acoustic tracking,the signal emission time is known.However,the true measurement reception time is unknown because it is corrupted by noise due to propagation delay.We augment the sensor’s signal reception time onto bearing measurements,and the information of the delay constraint is included in the original bearing measurements to compensate for the propagation delay. A Cubature Kalman Filter(CKF) is used for periodic acoustic source tracking, in which measurement prediction cannot be obtained directly because the sensor’s position at the true measurement reception time is unknown.We solve this problem by using the implicit Gauss-Helmert Sensor Model (GHSM) for estimating the sensor’s position,which consists of the sensor’s motion equation and the known measured sensor’s signal reception time equation related to the state. Then a CKF based on the GHSM (CFGHSM) is developed for periodic acoustic tracking. Illustrative examples demonstrate that the CF-GHSM algorithm is better than other algorithms for periodic acoustic source tracking.

1. Introduction

In the engineering application area, acoustic sources can be divided into two categories: one is aperiodic acoustic sources,and the other is periodic acoustic sources. Aperiodic acoustic sources widely exist in practice.However,there also exist some phenomena which cause periodic acoustic sources in a variety of practical applications. For example, the rattles of trains,sound periodically emitted by microphones in unmanned cars,and the beacon, communication modem, transmitting projector, or other known periodic acoustic sources carried in Autonomous Underwater Vehicles (AUVs).

For aperiodic acoustic source locating or tracking, abundant studies have been performed in Refs.. The existing methods can be divided into four categories, i.e., highresolution spectral estimation, steered beamforming, time delay estimation, and target motion analysis. The first type of methods can solve multiple-source location or tracking regardless of whether the incident energy sources are coherentor incoherent, but it is sensitive to the modeling error due to sound reverberation and computationally intensive.The second type of methodstransmits a signal without loss,but it provides a relatively poor resolution,and may not have a good performance for real-time applications since it is computationally intensive. The third type of methods is more realtime in applications. A typical location estimation method is the Time Delayed of Arrival (TDOA) estimation, which estimates the delay time based on a cross-correlation of paired microphone signals. TDOA estimation has a relatively high accuracy, but the iterations used in some of these algorithms require good initialization.Besides,these methods use a microphone arrayor multiple platforms for acoustic source localization or tracking. The fourth type of methods is applied in general application scenarios, in which a sensor is deployed on a maneuvering platform and then the target trajectory is observable. This method considers the geometric constraint of time delay, and the target state is estimated using a BOT algorithmbased on the augmented target state. The geometric constraint of propagation delay is depicted in Fig. 1.The target emits a signal at time t, and after the propagation delay time δ, the signal propagates and reaches the sensor at time t. That is,

where r is the distance between the target and the sensor, and cis the signal propagation speed in the medium (air or water). In the estimation process, the propagation delay time δ is augmented onto the target state vector, and a propagation delay constraint is included in the motion model.Therefore, the prediction state with an implicit constraint is obtained by a successive approximation iteration of the kinematic components and the delay time δ, but this method may lead to divergence due to a measurement error or other uncertainties. To reduce the errors of estimation, the emission time tis treated as a variable and included in the state in Ref., and the delay constraint is augmented onto the target kinematic state to build a Gauss-Helmert Model (GHM),then a Gauss-Newton algorithm is applied to obtain a prediction iteratively.

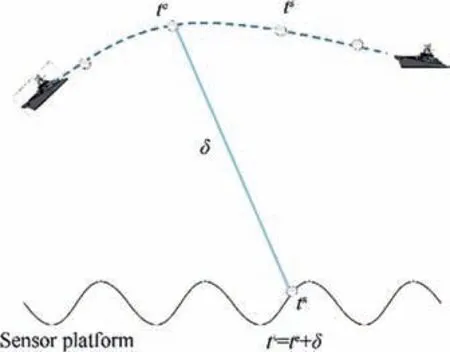
Fig. 1 Acoustic sensor receives delayed measurements after propagation delay δ.

However, periodic acoustic sources contain more information than that of aperiodic acoustic sources, and we can improve the performance by making full use of the extra information. Besides, periodic acoustic sources are prone to being recognized by their own characteristics.Thus,in many application scenarios, we should actively explore or add periodic acoustic sources and utilize their characteristics to obtain better estimates. For example, in some hostile scenarios, if we locate or track an opposite target, we should look for the target of periodic sound as much as possible so that the target can be detected more easily and accurately. On the other hand, in order to avoid being accurately detected by the opposite side,we can reduce the mechanisms and the factors which facilitate the work of a periodic vocalization system, but in some cooperative scenes, we should emit acoustics periodically for friendly parties to detect and track more accurately.

Although periodic acoustic source tracking has many practical applications, few studies have been concerned with it. In Ref., researchers utilized the characteristics of the periodic and harmonic of a vibrating model, and the location of the acoustic source was estimated through the Doppler effect which was included in the scatter signals. The problem of tracking an AUV with periodic sonar transmission in shallow water was addressed in Ref., which considered multi-path propagation caused by the multiple reflections or scatterings from the boundaries. However, currently existing periodic acoustic tracking methods are only confined to specific application scenarios in which the information of multi-path or Doppler effect is considered. Thus, the tracking methods proposed in Refs.cannot be applied directly in general application scenarios.

In general application scenarios, the state of an acoustic source is estimated from noisy measurements collected by a single passive sensor or observer, which is commonly referred to as Target Motion Analysis (TMA). Based on TMA,aperiodic acoustic tracking methodshave been studied,which compensate for the propagation delay information in the prediction step, but the prediction is obtained by approximation iteration. Obviously, it is not an accurate prediction.Besides, to estimate the state of the target and the emission time simultaneously,these methods augment the emission time onto the state vector. Since the emission time is random, the updated estimates are from different emission times in all Monte Carlo runs. In performance evaluation, we need to extrapolate the updated estimates to the common measurement reception time before the mean is computed. However,under this framework, for periodic acoustic source tracking,the emission time is known, and the updated estimates are from the same emission time in all Monte Carlo runs, so performance evaluation can be carried out directly and accurately.

Therefore,in this paper,periodical acoustic source tracking with noise-corrupted bearing measurements and measurement reception time in general application scenarios is investigated.Unlike the periodic acoustic source tracking method in Ref.this paper compensates for the delay information in a measurement model. It does not need to estimate the delay time and range difference. Specially, the periodic acoustic source tracking algorithm in this paper has three characteristics. Firstly,since the state transition matrix is explicit, prediction can be carried out without approximation, and performance evaluation can be performed accurately without extrapolation.However, this algorithm causes a new problem that the measurement reception time is corrupted by noise due to propagation delay, and the true measurement reception time without noise disturbing is unknown. Secondly, the measurement model consists of two-dimensional vectors.The sensor’s signal reception time related to the state is used to augment the original angle measurements, which not only provides additional information to the estimation, but also satisfies the physical rules of the propagation delay constraint.Thirdly,this method includes the delay constraint information in the update step of the estimation cycle. However, the Unscented Gauss-Helmert Filter (UGHF)includes delay constraint information in the approximated prediction step of the estimation cycle.

The remaining paper is organized as follows. In Section 2,the periodic acoustic source tracking problem with propagation delay is formulated as a dynamic estimation problem based on a state transition model,received bearings,and measured signal reception times. In Section 3, a periodic acoustic tracking algorithm is developed based on an implicit sensor model.In Section 4,numerical examples illustrate the effectiveness of the proposed tracking algorithm.

2. Problem formulation

3. CF-GHSM algorithm for periodic acoustic source tracking

Since the dynamic system formulated in Section 2 consists of a nonlinear Gauss-Markov transition model and a nonlinear measurement model, nonlinear filters will be applied for state estimation.

The performance of an Unscented Filter(UF)is vulnerable to the parameter κ（κ=3-n）.When the dimension of state is over 3 and κ is negative, poor performance or filtering divergence may appear. Compared to a UF, a CKF is applicable to high-dimensional nonlinear filtering. For the number of sample points,a CKF has one less sampling point in each sampling. Thus, a CKF has a faster computation than that of a UF.Since UF-computed covariance matrix is not always guaranteed to be positive definite, a CKF has better estimation accuracy and numerical stability than those of a UF.Therefore, in this section, we will use a CKF to perform nonlinear state estimation. However, this algorithm is not a commonly used CKF because the true measurement reception time is unknown, which needs to be estimated from implicit sensor motion equations.

Based on the target motion model described in Eqs.(2)-(4),a CKF is used for periodic acoustic tracking, which includes state prediction and update steps.

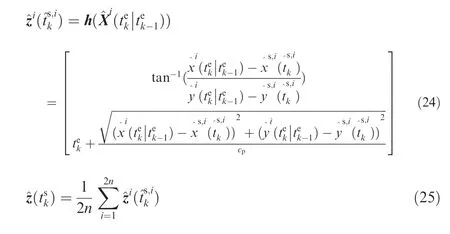
Remark 2. The predicted measurement includes two components,one is the bearing prediction,and the other is the sensor’s signal reception time prediction, which obeys the physical rules of propagation delay constraint. Therefore, the augmented measurement compensates for the delay in its measurement update step, and adds information to the estimation process.

In conclusion, for the periodic acoustic tracking algorithm formulated above, we complement the delay constraint information in the state update step by Eq.(26).That is,unlike aperiodic acoustic tracking algorithms,we add the information in the state update step instead of the prediction step.Besides,we use the information of known emission time. These all contribute to improving the tracking performance of a periodic acoustic source.

4. Illustrative examples

In this section,the performance of the periodic acoustic source tracking algorithm proposed in this paper will be compared in an experimental target tracking scenario with other possible tracking approaches.

By the utilization of the propagation delay and known emission time for periodic acoustic source tracking,three kinds of tracking algorithms are considered. The first kind of tracking algorithms neglects all the delay constraint information completely. The second kind of tracking algorithms utilizes the delay constraint information incompletely. The third kind of tracking algorithms utilizes the delay constraint information and the known emission time information completely.

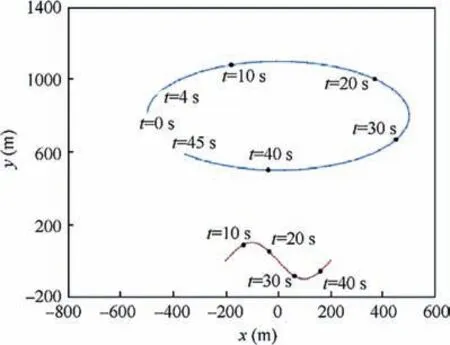
Fig. 2 Scenarios for targets.

All the possible kinds are tested using a simulated surface/air/underwater target.The single target in the scenario makes a clockwise Coordinated Turn (CT) motion in Fig. 2.

For the nearly CT model, the state vector is

The delay expression used in the experiments is given by Eq. (4) with c≈344 m/s in surface/air. The target moves at 15,22,50,or 100 m/s.The first three speeds indicate a normal,fast,or very fast surface target.The speed of 100 m/s indicates a helicopter. Similar test scenarios are also generated for an underwater target, where the speed of sound is given in Eq.(4)with c≈1484 m/s.In this paper,the signal emission time interval T=1 s. The initial target position is at (-500,800) m.The covariance of the initial state is

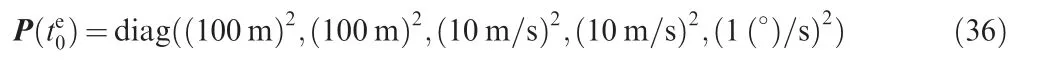
The acquired acoustic sensor bearing measurements are corrupted by zero-mean white Gaussian noise,and the covariance of the bearing measurements error is set to be R=（0.4）. The measurement reception time error is also zero-mean white Gaussian with covariance R=0.01 s.

Three approaches will be compared in a simulated target tracking scenario, i.e.,

(2) CF-BO: This approach utilizes the delay constraint information incompletely. It uses a CKF based on the bearing-only measurement to track the periodic acoustic source, and it also knows that the sensor receives bearing measurements with propagation delay compared with CF-NODELAY.

(3) CF-GHSM: This approach utilizes all the delay constraint information and the known emission time information completely,and it is the approach this paper has proposed.

We investigate the performance of periodic acoustic source tracking algorithms from several aspects.

4.1. Root mean square error

where i is the run index,N=500 is the number of runs,and K is the number of time indices in the scenario.

The position RMSEs versus time index k for the three approaches are considered for each simulated target.Figs. 3-4 show the position RMSE of the target in surface/air. It can be seen that the CF-GHSM outperforms the other approaches. The speed of sound is 344 m/s. For a slow-moving target (shown in Fig. 3), the RMSE of the CF-GHSM starts to decrease at the beginning, but the RMSEs of the CF-BO and the CF-NODELAY start to decrease around time 12 s. For a target moving with a normal speed (shown in Fig. 4 (a)), the CF-NODELAY algorithm has larger errors after 40 s. For a fast-moving target(shown in Fig. 4 (b)), the CF-GHSM and CF-BO algorithms converge at time about 20 s and 30 s, respectively. The RMSEs of the CF-GHSM and the CF-BO converge to a constant after 40 s. This is because the target is close to the sensor between the time of 40 s and 45 s when it has finished a periodic motion (Fig. 2).

Fig.5 is the target position RMSEs under water.The speed of sound is 1484 m/s.It can be seen that overall,the algorithm of the CF-GHSM shows the best performance. When a target moves at 10 m/s or 20 m/s,the RMSEs of the CF-GHSM and the CF-BO start to decrease around 10 s.

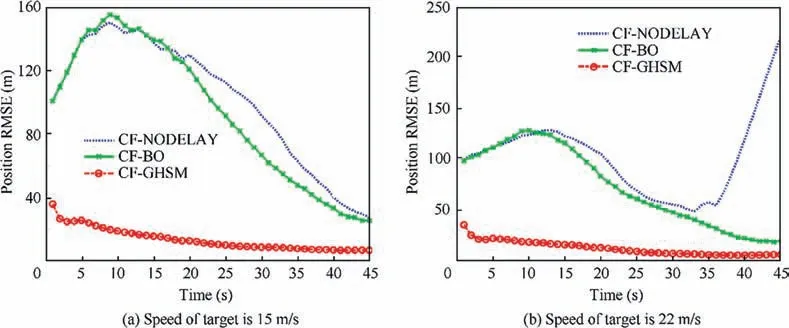
Fig. 3 Position RMSE versus time index k for a surface target.

Fig. 4 Position RMSE versus time index k for a surface target and an air target.

Fig. 5 Position RMSE versus time index k for an underwater target.

4.2. Influence of the measurement error on the RMSE

Fig.6 shows the position RMSEs of the CF-GHSM in the case of the bearing measurements error R=（1）and the measurement reception time error R=10sor R=10sfor a surface target and an air target, respectively. The speed of sound is 344 m/s. It can be seen that the RMSE decreases with a decrease of the measurement reception time error for a slow-moving target and an air target.

To show the performance with a larger bearing error, the overall position RMSE results for the bearing error covariance R=（1）are also included in Table 1.It can be seen that the tracking error increases with an increase of the measurement angle error. We can also see that the CF-GHSM outperforms the other approaches in all the test cases.The reason is that the CF-GHSM compensates for the delays in the measurement model. This additional information yields better estimation accuracy.

Fig. 6 Position RMSE of CF-GHSM versus time index k for a surface target and an air target.

Besides, we observe that the CF-GHSM has better performance for a slow-moving target than that for a fast-moving target. The reason is that fast-moving targets have a higher bearing change rate, which results in a larger error for state estimation.

4.3. Consistency analysis and significance of performance improvement

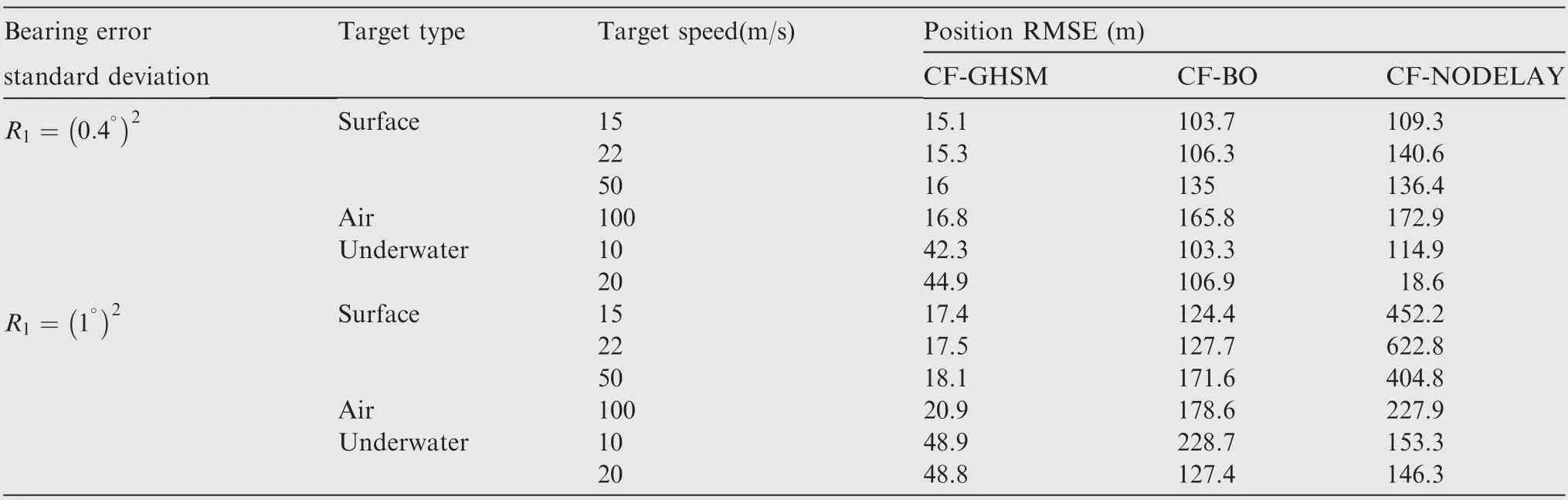
Table 1 Averages of position RMSE per run for simulated targets.

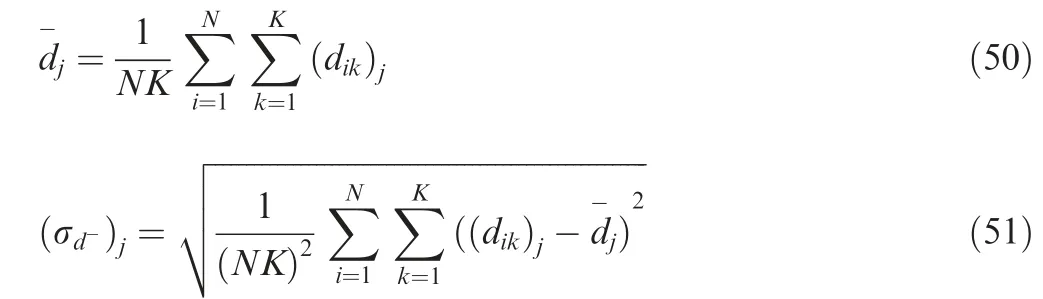
Table 2 Statistical comparison of CF-GHSM with CF-BO and CF-NODELAY.

The results for N=300 runs are shown in Table 2 when the bearing error covariance is R=（0.4）and the measurement reception time covariance is R=0.01 s. It can be seen that the ratios between the mean and standard error are greater than 1.96 in all scenarios (1.96 is the threshold of the normal distribution 97.5% probability). This means that the CF-GHSM has a statistical improvement over the CF-BO and the CF-NODELAY.

5. Conclusions

This paper presents a periodic acoustic source tracking approach based on the augmented measurement, which augments the measurement reception time corrupted by noise onto the bearing measurement. A CKF is used for estimating the state of a periodic acoustic source.In the measurement update step,the true measurement reception time is estimated from an implicit Gauss-Helmert equation which is composed of the motion equation of a sensor and the measurement reception time equation related to the target state by propagation delay.Thus, a CF-GHSM approach for periodic acoustic source tracking is developed. Experimental results show that the CF-GHSM approach is more suitable and accurate for periodic acoustic source tracking than other approaches. This algorithm obtains better estimation performance due to it following distinguishing properties.Firstly,it includes the propagation delay in the measurement model. Secondly, it compensates for the delay constraint information in the estimation cycle in the update step.Thirdly,it utilizes the information of the known emission time.

s

The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.

s

This work was supported in part by the National Key Research and Development Plan, China (No.2017YFB1301101) and the National Natural Science Foundation of China (Nos. 61673317 and 61673313).

Appendix A. The function F（·） in Eqs. (16)-(19) is an abstract function, which depends on concrete application scenarios.

In conclusion, From Eqs. (A6-A17), Broyden’s update method is simplified to Eqs. (16)-(19).