Optimal predictive sliding-mode guidance law for intercepting near-space hypersonic maneuvering target

Bolun ZHANG, Di ZHOU

School of Astronautics, Harbin Institute of Technology, Harbin 150001, China

KEYWORDS Adaptive sliding-mode control;Near-space hypersonic aircraft;Neural networks;Optimal control;Predictive guidance law

Abstract The design of optimal guidance law for intercepting a near-space hypersonic maneuvering target with bounded inputs is considered. Firstly, a maneuvering model for near-space hypersonic aircraft is given. Then, the aircraft acceleration prediction can be obtained using this model with two neural networks. By using the target acceleration prediction, which is taken into account when calculating the Zero Effort Miss(ZEM),an optimal sliding-mode guidance law is proposed to fulfill the guidance task.An adaptive sliding-mode switch term is designed to deal with actuator saturation and prediction errors.Finally,numerical simulations show that the proposed guidance law can reduce the energy consumption and the terminal acceleration command of the interceptor effectively.

1. Introduction

In recent years,the technique of near-space hypersonic vehicle has been developed rapidly.The strong maneuvering nearspace vehicle has brought great challenges to defense technology. For example, the design of a terminal guidance law for intercepting the near-space hypersonic maneuvering target whose maximum acceleration is very close to that of the interceptor missile has become an attractive topic.In order to intercept high-speed and high-maneuverability aircraft, some researchers studied the cooperative guidance schemes of multiple missiles.For example,Wang et al.and Shaferman et al.used a cooperative guidance strategy,where multiple interceptors attack the target from different directions simultaneously to reduce the impact of the target’s maneuvering. Shaferman and Oshmanproposed a strategy that two interceptors attack the target at a certain distance apart.The key idea of the strategy is to improve the interception performance of the trailing missile by the leading missile collecting the superior information.The aforementioned cooperative guidance schemes based on multiple missile interceptors must cost much more than a guidance scheme based on a single missile interceptor. Moreover,it is hard to realize the real time communications between multiple missiles.

The cost of a near space interceptor missile must be much more than an endo-atmospheric interceptor missile.Therefore,herein we study the design of a terminal guidance law for a single missile intercepting near-space hypersonic maneuvering targets.In the terminal guidance process of a near space interceptor, its flight path is controlled by reaction control thrusters. So it is necessary to consider the energy optimization of the interceptor. However, there are two main difficulties to design an optimal guidance law in this case. The first one is that traditional optimal guidance laws will become suboptimal when the target is maneuvering.Especially when the maneuver is strong enough, those guidance laws do not show any advantage over the Proportional Navigation guidance law.The second difficulty is that,in near-space,the maximum value of the acceleration of a near-space hypersonic flight vehicle is even close to that of an interceptor missile.This usually causes the saturation of the control input of the interceptor and then the failure of an interception.In addition,The guidance strategies based on game theory was proposed using energy consumption as an indicator of a game.However,the above game guidance strategies are so complicated that their heavy calculation burden is hard to meet the requirement of real time applications.

If the target acceleration can be well predicted and the prediction is applied to the design of a guidance law, the above two difficulties can be overcome. Guo et al.introduced the ZEM and Zero Effort Velocity(ZEF)into the design of a guidance law and obtained an optimal solution in a uniform gravitational environment. Tournes et al.and Kumar et al.designed a predictive guidance law for intercepting ballistic missiles according to the characteristics of ballistic missile in different flight segments.For the near-space interception problem, the above methods are not applicable because the target aircraft is also subject to aerodynamic forces. Therefore, how to predict the acceleration of the near-space aircraft has become the first problem to be solved in this work. The traditional Singer modeland multi-model filtering methodscan only be used to estimate the acceleration of target,but cannot be used to predict the target acceleration. Aiming at estimating the acceleration of a periodically maneuvering nearspace vehicle, Li and Xiongproposed an Adaptive Nonzero Mean Sine Wave(ANM-SW)model.This model is based on the Constant Jerk model,but it needs the prior information on the target maneuvering period and maximum maneuver acceleration. In addition, the model does not propose a method to predict the target states. Maeder et al.used Interacting-Multiple-Model (IMM) method to estimate the target states and then extrapolate. However, in the models used in the above two methods, the aerodynamic force, an important factor that affects the flight status of the nearspace vehicle, is not considered. Li et al.proposed a trajectory prediction method based on aerodynamic acceleration empirical mode decomposition Li and Jilkovintroduced a target maneuvering model that includes aerodynamic force to estimate the target accelerations generated by lift and drag,respectively. In order to obtain the prediction of the acceleration of a near-space hypersonic target, we first propose a maneuvering model related to aerodynamic parameters inspired by Li and Jilkov.Then, we can get the predicted value by using the aerodynamic parameters to train two neural networks. Recurrent Neural Network (RNN)and General Regression Neural Network(GRNN),which have good performance in learning nonlinear features on time series,are used to complete this task. However, using this method to obtain a more accurate prediction requires a sufficiently long observation time.Therefore,an auxiliary observer is necessary to track the target before the target seeker on the interceptor finds the target.

When the predicted value of the target acceleration is obtained, it can be applied into the calculation of the ZEM to obtain the predicted ZEM. Using the predicted ZEM, we can get the analytical expression of the optimal guidance law according to the optimal theory.However, due to the errors between the prediction of acceleration and the actual value,the guidance law is required to have strong robustness. A purely optimal guidance law does not have this characteristic.Pang and Wangand Dong et al.introduced the optimal sliding mode control of uncertain systems. To improve the robustness of an optimal guidance law,Zhou et al.combined optimal control with sliding-mode control and proposed an optimal sliding-mode guidance law. Wang et al.proposed a stochastic sliding mode guidance law based on optimal control theory considering measurement noise.Refs.had ignored a very important feature (actuator saturation), which always causes performance deterioration and even system instability in practical systems. Goebeland Lebedevconsidered the saturation problem of optimal control and sliding mode control respectively.There is also a problem worth noting that the disturbance, caused by the prediction error in the ZEM dynamic equation, is a function related to the acceleration prediction error and time to go. Therefore, it is difficult to have priori knowledge on its upper bound.Zhu et al.applied an adaptive sliding mode control method to aircraft attitude control system where the adaptive sliding-mode term solves the problems of parameter uncertainty and unknown disturbance.In this work,we consider designing an adaptive sliding mode switch term to deal with the prediction error and actuator saturation.

This paper is organized as follows. In Section 2, a new maneuver model for the near-space vehicle is given. Based on the model, a method for predicting the target acceleration is introduced. In Section 3, by decoupling the 3-dimensional nonlinear guidance model, an optimal sliding mode guidance(OSMG) law is introduced. By designing an adaptive sliding mode switch term, the stability of the guidance law is ensured in the presence of prediction errors and actuator saturation.Then, some numerical simulations in Section 4 demonstrates the effectiveness of OSMG law. Finally, some concluding remarks will be made in Section 5.

2. Prediction of target acceleration

The acceleration of a near-space hypersonic flight vehicle are generated by aerodynamic force. It has various forms of maneuver with long periods.Some traditional maneuver models, such as Singer model,Constant Acceleration (CA)model,and Constant Jerk(CJ)model,are difficult to exhibit the property of the maneuver of a near-space hypersonic vehicle. This makes it difficult to predict the future accelerations of a near-space hypersonic vehicle by using a traditional maneuver model even if the acceleration can be estimated via using this model. In this section, we introduce a maneuver model in terms of aerodynamics to predict the accelerations of a near-space aircraft by iterative calculations.

For a near-space vehicle, the acceleration is generated by the aerodynamic force, which is projected into the flight path coordinate system.The origin of the flight path coordinate system is located at the target mass center.The X-axis points to the direction of target velocity,the Y-axis is perpendicular to the X-axis and located in the plane which contains the Xaxis and is vertical to the horizontal plane, and the Z-axis is determined according to the right-handed rule. In addition,the prediction of the target acceleration needs to be completed by a filtering and predicting algorithm. The value of the predicted acceleration is related to the observation inertial coordinate system,which is presented in Fig.1.The origin‘‘O”of the inertial coordinate system is located at the position of the observer (radar). The Y-axis is the connection between the earth center and the observer while the positive direction pointing to the sky. The X-axis is perpendicular to the Y-axis and located in the plane containing the earth center,the observer and the initial target position. The Z-axis is determined according to the right-handed rule.

Firstly, three state variables are introduced as

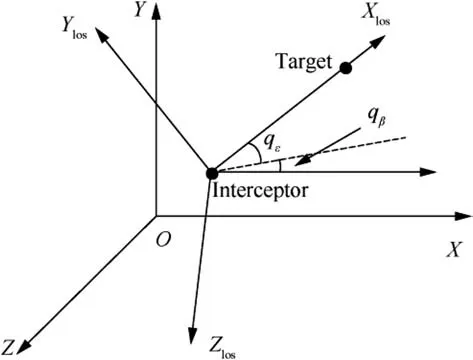
Fig. 1 Inertial coordinate system and line of sight coordinate system.

Eq. (7) is a nonlinear model. It is natural to use the Extended Kalman Filtering (EKF) method to estimate X.State equations and measurement equations can be described

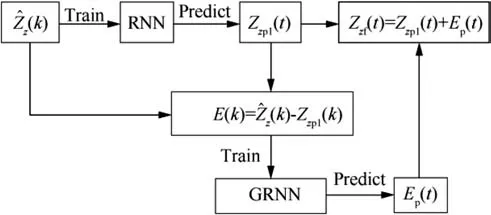
Fig. 2 Process to get the prediction of Zz

This prediction method requires just the target position measurements continuing for a long enough period of time.Simulations under different scenarios show that when using this model to estimate the states of a near-space target,it takes about 30 s for each axial acceleration estimation error converging to a bound within 1 m/s. Details about this part will be explained in Section 4.In the terminal guidance stage,it is difficult for the interceptor to obtain the acceleration prediction of the target by itself, and so an auxiliary radar is required to observe the target and then send the target acceleration predictions to the interceptor.

Remarks 1. For a near-space hypersonic vehicle in the cruising phase,its maneuverability is provided by aerodynamics.According to Eqs. (1) and (7), it can be seen that the aerodynamic acceleration is related to the aircraft’s position, velocity,aerodynamic coefficient, mass, and equivalent reference area.The mass and the equivalent reference area can be regarded as constants and the aerodynamic coefficient is determined by the aircraft’s velocity, attack angle, and sideslip angle. Compared with Singer model, the model proposed in this paper takes into account the specific factors that affect the acceleration. So, the estimation for target acceleration is more accurate. In addition,it is more reasonable to regard Z，Z， and Zinstead of acceleration as slow time-varying random processes because in the terminal stage of its cruising phase the aircraft is not liable to change its maneuver scheme due to the constraint on its landing conditions.

3. Optimal sliding-mode guidance law

The line of sight coordinate system(X-Y-Z),as shown in Fig. 1, depends on the position of the interceptor and the target at the current time. The guidance dynamics in the line of sight coordinate system is represented by

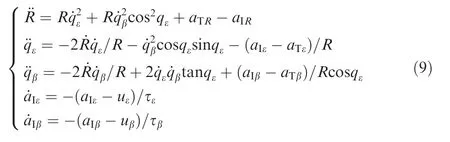
where R is the relative range between the interceptor and the target; qand qare the line of sight angles; a， a， and aare the target accelerations along the line-of-sight axes;a，a， and aare the interceptor accelerations along the line-of-sight axes; uand uare the control inputs; τand τare time constants of the interceptor.

In this problem, ais not controllable. We convert the nonlinear model (9) to a linear model. Then, the 3-dimensional guidance problem becomes two uncoupled 2-dimensional problems. Taking the longitudinal plane as an example, the optimal sliding mode guidance law considering the target acceleration prediction will be introduced.

3.1. Optimal guidance law considering the acceleration prediction

When qand qare small, we can get the linearized dynamic model of Eq. (9) in the longitudinal plane as follows:

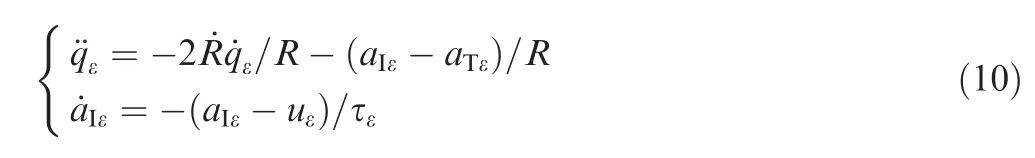
The relative dynamics between the interceptor and the target in the longitudinal plane are shown in Fig. 3, where qis the initial line-of-sight angle and Zis the component of the current relative range perpendicular to the initial line of sight.To apply the theory of optimal guidance law, the purpose of control is to make the predictive ZEM converge to 0.

The predictive ZEM is defined as

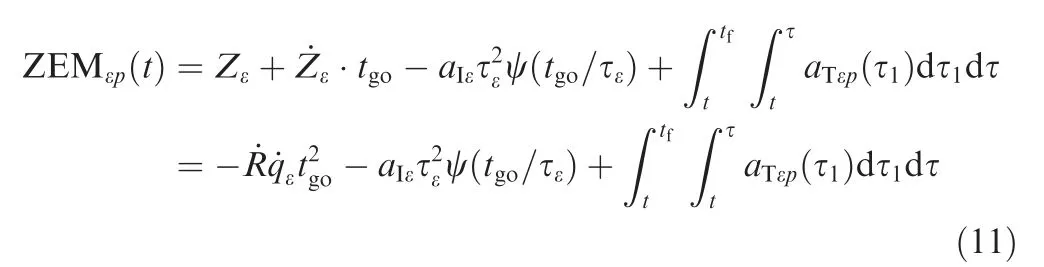
where tis the final interception time,

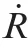
is the transform matrix from the inertial coordinate system to the line of sight coordinate system

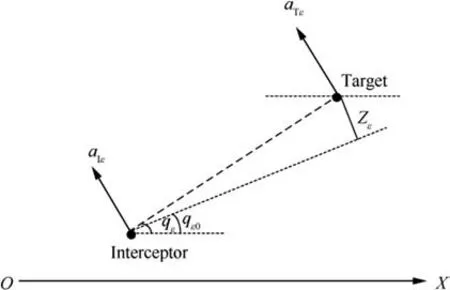
Fig. 3 2-dimensional guidance geometry.

Remarks 2. The existing optimal guidance laws for intercepting a maneuvering target usually ignore the target acceleration during the design process, i.e., the ZEM is defined as

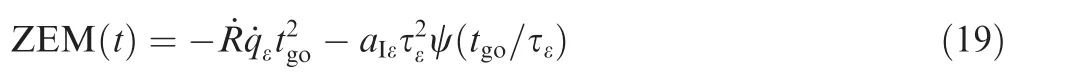
To compensate for the target acceleration, an additional compensation term is introduced into the guidance law,which makes the guidance law suboptimal.The suboptimal guidance law is designed as

3.2. An adaptive sliding-mode switch term to deal with the prediction errors and saturation

Since the predicted values are used in the optimal guidance law,strong robustness of the guidance law is necessary to deal with prediction errors, estimation errors of the line-of-sight angular rate and the actuator saturation. The sliding-mode control method is a well-established robust control algorithm that can handle bounded matched disturbances with different forms. So, in this work, we design a sliding-mode switch term to deal with the prediction errors and saturation.

When there exist prediction errors,the true value of ZEM is

where urepresents the maximum acceleration generated by the interceptor.

There exists a constant δ that makes the following inequality

holds.

The OSMG law has the following form:

where uis calculated from Eq. (17) and uis the switch term. Without loss of generality, suppose |d（t）| has an upper bound d, i.e., |d（t）|≤d. Then, the switch term ucan be designed as

where μ>1，p>0，^γ is the adaptive gain,and ^d is the adaptive estimate of d. The initial values ^d（0）>0 and ^γ（0）>0.

Theorem 1. For the ZEM system consisting of Eqs. (11) and(24), ZEMwill converge to 0 with the OSMG law (27).

Proof of Theorem 1. Consider the following Lyapunov function:

Remarks 4. The OSMG law does not avoid the saturation of the control input, but guarantees the stability under saturation,making it possible to take full advantage of the interceptor’s maximum maneuverability.

Remarks 5. In this work,the essence of OSMG law is to design the optimal guidance law according to the target acceleration prediction and to compensate for the prediction errors via using the sliding mode switch term.However,when the target acceleration is predicted for a long period of time, a large acceleration prediction error may be generated, making the energy consumption even greater than the case where no prediction is used.Therefore, we can adjust the ZEMto the following form:

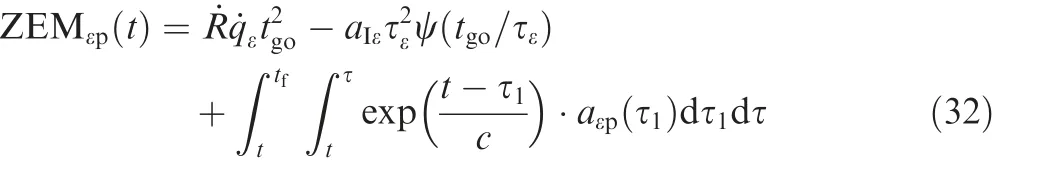
where c is a positive constant.If we have confidence in the target acceleration prediction,then we may assign a large number to c;otherwise,assign a small number to it.When c →∞,Eq.(32)is equal to Eq. (11). When c →0,Eq. (32)is equal to Eq.(19), meaning the guidance law doesn’t consider the predicted information.

4. Numerical simulations

In this section, we select a hypersonic aircraft gliding in nearspace as the target. The lift-to-drag ratio of the aircraft is about 3:1, and the velocity of the aircraft is about 12Mach.The flying altitude is about 30 km to 40 km. The acceleration estimation results for the target are given firstly. Then use the estimated value of the target acceleration and the measurements of line-of-sight provided by the interceptor seeker to estimate the line-of-sight angle rate required by the OSMG law. The simulation results of target state estimation are all compared with the results of using Singer model, ANM-SW model,and IMM filter,respectively. The target state prediction results will be compared with the IMM prediction method.Then, the interceptor uses OSMG law to intercept the target. We consider a more complicated situation, that is,assuming that the target discovers the interceptor and makes an abrupt escaping maneuver with a maximum constant acceleration at（t-1） s.The interception results under the OSMG law are compared with that under the Augmented Proportion Navigation (APN) law and the Optimal Guidance Law(OGL). Finally, we will discuss the convergence time of the proposed model for state estimation of near-space targets,and analyze the influence of large tracking errors within short tracking time on the predictive guidance law.

The maximum value of the interceptor is set to be 25 m/s,and the time constants τ= τ=0.1. The starting time of the interceptor’s terminal guidance is taken as t=0 s. We start estimating the target acceleration from t= -96 s and predicting it from t=0 s to obtain the ZEM（t） and ZEM（t）. The information of interceptor and target at t=0 s is shown in Table 1.

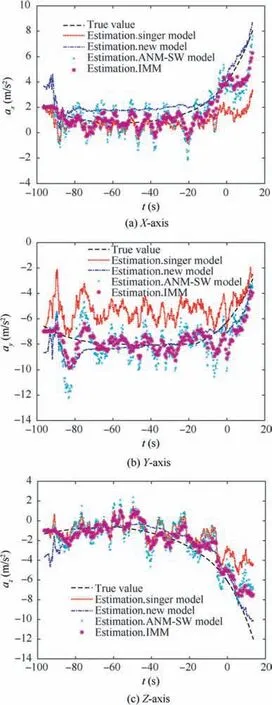
Fig. 4 Estimations of target acceleration.

Table 1 Initial information of interceptor and target.

Fig. 5 Time when the acceleration estimation error is stable within 1 m/s2.

Fig. 6 Estimations of the line-of-sight angular rate.

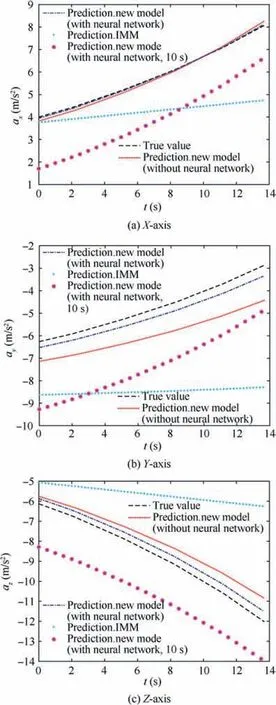
Fig. 7 Predictions of the target acceleration.

For the interceptor working in the near-space, the maneuverability of the interceptor does not have an apparent advantage over the maneuverability of target. From Fig. 9, it is obvious that in the most time of terminal guidance process,the magnitude of acceleration under the OSMG law is less than that under the APN law and OGL,and so the energy consumption in the terminal guidance process under the OSMG law is much less than that under the APN law and OGL.

Fig. 8 Prediction errors of the target final position as the terminal guidance proceeds.

Next,consider a more complicated situation that the target finds the interceptor at（t-1） s and makes an evasive maneuver.Fig.11 shows the control inputs of the three guidance laws in this case where the target lateral acceleration aafter the evasion maneuver is close to the interceptor’s maximum maneuverability.That makes it difficult to intercept the target.The simulation results of the three guidance laws when the target makes an evasive maneuver are shown in Table 3 where the final miss distance under the OSMG law is only 0.79 m while that under the APN and OGL is 3.99 m and 3.07 m, respectively.Thus,the advantage of OSMG law in accuracy is apparent compared with the two other guidance laws.Moreover,the energy consumption is still less than the other two guidance laws in this case with abrupt target maneuver. However, the energy consumption of OSMG law in this case with abrupt target maneuver is obviously larger than that in the previous case without abrupt target maneuver, because the abrupt target maneuver had not been predicted.

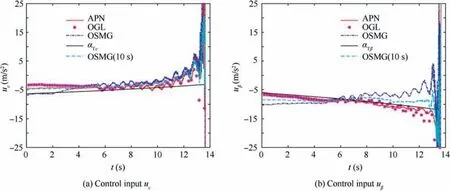
Fig. 9 Control inputs of interceptor.

Table 2 Simulation results.

We have carried out 100 runs Monte Carlo simulation and counted the energy consumptions and the final miss distances of the three guidance laws. The results are shown in Table 4.The subscripts ‘‘min”, ‘‘max” and ‘‘ave” represent the maximum, minimum, and average values, respectively. It is shown in Table 4 that the maximum miss distance under the OSMGlaw is 0.82 m,while the minimum miss distance under the APN law and that under the OGL is 3.12 m and 2.66 m,respectively.The OSMG law avoids some unnecessary maneuvers so that its control inputs are smaller than that of the other two guidance laws, making the interceptor be more capable of dealing with model errors and abrupt target maneuvers at the final stage of terminal guidance. However, when the time for state estimation is short, a large final miss distance may occur. In addition, the advantage of the OSMG law in energy is no longer obvious.

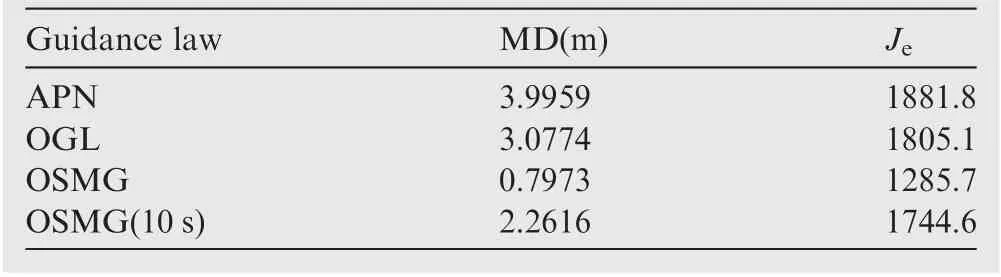
Table 3 Simulation results when the target makes an evasive maneuver.

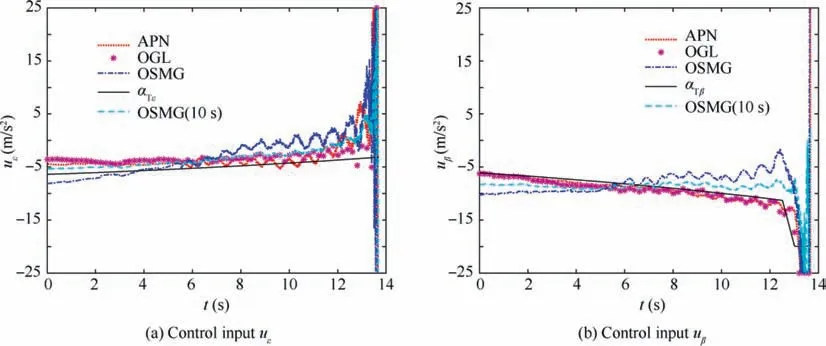
Fig. 11 Control inputs of the interceptor when the target makes an evasive maneuver.

Table 4 100 Monte Carlo simulation results.

Through the above simulation results,we can conclude that the OSMG law can effectively reduce the energy consumption of the interceptor if the tracking of the target can be carried out at least 30 s before the start of terminal guidance.In addition,it has a great advantage in intercepting maneuvering targets whose maneuverability is comparable to that of the interceptor.

5. Conclusions

In this paper, we propose an optimal sliding-mode guidance law based on a target acceleration prediction model. By using the proposed target acceleration prediction model, more accurate estimations for the target acceleration can be obtained,and this is also beneficial to obtain more accurate line-ofsight angular rate estimations. By using the neural networks to predict the trend of variations of aerodynamic parameters,the prediction of target acceleration is obtained and applied to designing the optimal sliding-mode guidance law. There are three main advantages for the designed guidance law. (A)The stability of the guidance system in the presence of prediction errors and actuator saturation is guaranteed by introducing an adaptive sliding-mode switch term.The switch term also improves the robustness of optimal control. As a result, for intercepting a maneuvering target, especially a target with an abrupt target maneuver, the OSMG law has a smaller final miss distance than the APN law and OGL. (B) This guidance law makes the interceptor avoid unnecessary maneuvers by using the predicted information, and so the energy consumption is much less than other guidance laws without using the predicted information. (C) In most time of the terminal guidance process, the control inputs under OSMG law is smaller,making the interceptor be more capable of dealing with model errors and the abrupt target maneuver at the final stage of terminal guidance.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was supported by the National Natural Science Foundation of China (No. 61773142).