Impact of aperture on dynamic response of sandwich plates with aluminium face-sheets and PMI core based on an alternative finite element formulation and experiments

Zhen WU, Yongzhi LI, Dongjin ZHANG, Jie MEI, Xiohui REN,Rui MA

a School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China

b School of Mechanical Engineering, Xi ,an Aeronautical University, Xi’an 710065, China

KEYWORDS Dynamic response;Sandwich plates;Higher-order theory;Experimental tests;Finite element method

Abstract Apertures generally exist in the sandwich structures attributing to mechanical connection and lightweight, which might induce failure of such structures. Thus, it is required to realize the impact of aperture on mechanical behaviors of sandwich structures. If transverse shear deformations are unable to be described accurately, the reasonable prediction of dynamic behaviors of the form-core sandwich plates with apertures will meet severe challenges due to a large difference of transverse shear modulus at the adjacent layers. Thereby, such issue is less studied by using the efficient models and experimental testing,so an alternative sinusoidal-type finite element formulation is to be proposed to precisely predict dynamic response of the form-core sandwich structures with apertures. The proposed finite element formulation can meet beforehand compatible conditions of transverse shear stresses at the interfaces of adjacent laminates.In order to appraise strictly capability of the proposed model,experimental tests on natural frequencies of three groups of specimens with different apertures have been carried out. Moreover, four specimens in each group are tested to reduce the testing errors, which is less reported in the published literature. In addition,three-dimensional Finite Element Method (3-D FEM)is also selected to account for the good performance of the present model.Finally,the impact of aperture diameter on the natural frequencies of the sandwich structures is both experimentally and numerically investigated,which can serve as a reference for other researchers.

1. Introduction

Sandwich plates have gained their popularity in transportation, military, marine and civil structures owing to their light weight, high strength rate and modulus rate. In particular,sandwich plates have been widely used in aircraft radome,wing flap and aircraft elevator to reduce structural weight.Cut-outs in sandwich plates are often required to reduce the weight of the structure and meet the requirements of the work.Due to the large difference of material properties at the adjacent layers,the presence of apertures complicates the stress distribution of the sandwich structures,which seriously affects the dynamic response of these structures. Hence, a plate theory accurately predicting natural frequencies of sandwich plates with apertures and experimental tests is required.

Based on various plate theories,investigations on the vibration characteristics of sandwich plates have been carried out.The First-order Shear Deformation Theory (FSDT) has been utilized for the dynamic analysis of Functionally Graded Material (FGM), composite and sandwich plates due to its cheap computational cost.In the FSDT, transverse shear strain varies linearly with the thickness of plates, which will lead to an inaccurate dynamic response of sandwich structures with the soft transverse shear modulus. Therefore, various Higher-order Shear Deformation Theories (HSDT) have been applied for free vibration analysis of sandwich plates.Reddy’s higher-order theorywas utilized to study dynamic response of composite structures.Matsunagaimproved the order of displacement function to present a ninth-order model,which was used to investigate the dynamic characteristics of composite shallow shells under in-plane stress. Akavci and Tanrikuluutilized hyperbolic displacement models for dynamic analysis of laminated composite plates. Thai et al.presented a new inverse tangent plates theory. Based on the proposed model,the isogeometric analysis approach was used for the static and dynamic analysis of laminated composite plates.Mohammed and Cagriemployed nonlocal strain graded theory along with the higher order shear theories to consider the dynamic response of the functionally-graded microbeams resting on the elastic foundation. In the study of Wu et al., the vibration analysis of composite and sandwich plates was performed using the five-unknown higher-order theory. Safaei et al.investigated the dynamic response of nanocomposite sandwich plates subjected to thermal gradient and periodic mechanical loads by utilizing the mesh-free method in conjunction with the higher order shear deformation theory. Moreover, the zig-zag theory was also used to explore the dynamic behavior of sandwich plates. Sahoo and Singhdeveloped a zig-zag theory which can satisfy the traction-free boundary conditions at the top and bottom surfaces of the laminate and the transverse shear stress continuity at the interfaces.By means of the developed model, the dynamic stability behavior of laminated composite and sandwich plates was assessed.Di Sciuva and Sorrentistudied bending,free vibration and buckling performance of functionally graded plates through the Ritz method based on the extended Refined Zigzag Theory.

The stresses analysis near the hole regions of the composite panels has been widely investigated. Boayand Sivakumar et al.studied free vibration of laminated composite plates with cutout. Based on the strain gradient elasticity theory, Torabi et al.developed a hexahedral element to investigate the free vibration response of nano-plates containing circular cutout. Kasar et al.studied the stress concentration of laminated composite plates with different centrally located cutouts using ANSYS. Rajkumar et al.measured the dynamical properties of tensile and open-hole tensile composites using a free vibration technique. Results of the tensile testing indicated that the tensile strength and modulus decrease as the diameter of the central hole increases. Duan et al.investigated the circular hole-edge stress concentration of the composite plates through a theoretical model and physical tests. The testing results showed that the influenced area of stress concentration is within the range of four times of the hole radius. Various investigations have also been carried out for the hole-edge stress analysis of the composite laminate subjected to different loading conditions such as shear load,compression failure,uniaxial transverse compression bucking,tensile and shear failure.Moreover, the determination of stresses near the hole regions in different types of composite panels like laminated composite curved panels,singly-curved and doubly-curved composite plates,laminated composite skewed shells,Carbon Fiber-Reinforced Polymer (CFRP)cylindrical shellsand laminated composite spherical shellswas also concerned.

In the past, numerous researchers have investigated the impact of cut-outs on the stability analysis and the dynamic behavior using various plates theories. For instance, Kumar and Shrivastavainvestigated the free vibration response of thick square composite plates with cutout by developing a finite element formulation based on HSDT and Hamilton’s principle. Based on four-unknown displacement functions,Anil et al.studied the buckling behaviors of thick composite plates with cutouts under in-plane compressive loading. The dynamic behavior of the moderately thick plates with cutouts was investigated by Ovesy and Fazilati,where a third-order shear deformation theory of plates in conjunction with finite strip method was utilized. Using the First-order Shear Deformation Theory(FSDT)and the Classical Plate Theory(CPT),Awrejcewicz et al.studied the dynamic characteristics of symmetrically laminated plates of complex shapes and having different cutouts. Mehrparvar and Ghannadpourinvestigated the nonlinear behavior of thick functionally graded plates with cutouts based on the first order shear deformation plate theory.Do and Leeimplemented Isogeometric Analysis(IGA) method based on the quasi-3D Higher-order Shear Deformation Theory (HSDT) to study the free vibration of Functionally Graded Material (FGM) plates with complex cutouts. Vinyas et al.studied the vibration performance of smart magneto-electro-elastic composite plates with cut-outs using Higher-order Shear Deformation Theory (HSDT) in conjunction with finite element methods.Othmane et al.proposed a four-unknown plate theory for static and dynamic analysis of composite and sandwich plates. Furthermore, the four-unknown plate theory was extended to investigate the dynamic behaviors of FG-sandwich plates resting on elastic foundation.In the light of the four-unknown plate theory,Chikr et al.studied the buckling behaviors of FG-sandwich plates seating on elastic foundations. Employing the fourunknown plate theory, Rahmani et al.researched impact of boundary conditions on static and dynamic response of FGM sandwich plates.In order to reduce computational cost,Rabhi et al.proposed a three-unknown plate theory for buckling and free vibration analysis of FG-sandwich plates resting on the elastic foundations. Utilizing the generalize differential quadrature method, Al-Furjan et al.investigated the dynamic behaviors of the imperfect sandwich higherorder disk.More models can be found in the review article presented by Carrera.

On the other hand, a variety of numerical methods have been introduced to perform vibration and buckling analysis of composite and laminated structures, which include Rayleigh-Ritz method,the Finite Element Method(FEM),the Non-Uniform Rational B-Splines (NURBS)-based isogeometric analysis,the independent coordinate coupling method,the finite strip method,and extended Finite Element Method (XFEM).However, the dynamic response of sandwich plates with apertures has been studied by only a few researchers. The investigation on this issue was reported by Mondal et al.. The parameters affecting natural frequencies of sandwich plates with composite face sheets and Polyvinyl Chloride (PVC) core were investigated under free boundary conditions by means of an eight-node threedimensional solid brick element(C3D8R)in ABAQUS.Moreover,four sets of modal testing of samples without and with a central hole of different diameters were performed for comparison.Survey of literature reveals that the impact of aperture on natural frequencies of sandwich plates with metal face sheets and the Polymethacrylimide(PMI)form core is less taken into considerations by researchers.It is also found that,there is less reported investigation on the higher-order plate theory for the free vibration analysis of sandwich plates with apertures.Material properties at the adjacent layers of sandwich plates change largely, so transverse shear deformations play an important role. In order to predict precisely natural frequencies of sandwich plates, compatible conditions of transverse shear stresses at the interfaces are required to be fulfilled.The global-local higher-order theory proposed by Li and Liucan meet the compatible conditions of transverse shear stresses at the interfaces,while this model contains eleven independent displacement variables.In order to reduce the computational costs, displacement variables in the global-local higher-order model should be compressed. Therefore, there is a genuine requirement to propose an efficient and accurate model to study this issue.

The main objective of the present study is to propose an efficient finite element formulation using a Sinusoidal Global-Local Higher-order Theory (SGLHT) to investigate the impact of aperture on natural frequencies of sandwich plates.The proposed theory beforehand fulfills the compatible conditions of transverse shear stresses at the interface of adjacent layers. Moreover, seven independent displacement variables are merely involved in the proposed model, so that four displacement variables have been reduced in comparison with the precious global-local model.The Hamilton’s principle is employed to present the governing equation of motion.In-plane displacements of the proposed model SGLHT contain the first derivatives of transverse displacement, so that in-plane strains will contain the second derivatives of transverse displacement by utilizing the geometric equations. In order to guarantee convergence of finite element formulation,the first derivatives of transverse displacement functions are required to be continuous at the common edge of adjacent elements.Thus,this paper attempts to utilize the shape functions of the Discrete Kirchhoff Theory (DKT) elementto discretize the first derivatives of transverse displacement parameter,which can meet the compatible requirements on the shared boundary between adjacent elements. To check the validity of the present model, the experimental tests on the natural frequencies of sandwich plates with a central hole of different diameters have been conducted by the hammering method,which is less reported. Moreover, numerical examples based on 3D-FEM and various higher-order models are analyzed to assess the efficiency and accuracy of the present model. In the parametric study, the dynamic performance of sandwich plates is investigated for different hole diameters through experiments and numerical simulations. The testing data and comparative studies show that the proposed model is an effective higher-order plate theory for accurately predicting natural frequencies of sandwich plates with apertures. Numerical results show that the compatible conditions of transverse shear stresses at the interfaces should be not neglected for accurate prediction of natural frequencies of sandwich plates with aperture.Otherwise, it is hard to completely yield natural frequencies of thick sandwich plates attributing to the large change of transverse shear deformation at the adjacent layers of thick sandwich plates.

2. Mathematical formulation

A schematic of sandwich plate with one circle hole is shown in Fig. 1. In the light of three-dimensional elasticity analysis,the form of displacement field can be determined by using the requirements of interfaced-continuity conditions and free-surface conditions of transverse shear stresses. In order to meet these conditions, the local displacement functions will be superimposed on a sinusoidal higher-order displacement field.In-plane stress assumption will be adopted,so that transverse displacement is merely a function of x and y coordinates.Thus,an initial displacement model for sandwich plates can be presented by

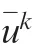
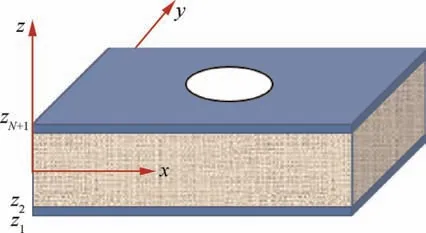
Fig. 1 A schematic of sandwich plates with one hole.

Inserting Eq. (1) into the geometric equation, the strains can be acquired. Afterward, introducing transverse shear strains in the constitutive equation, the transverse shear stresses for a cross-ply composite plate can be expressed as

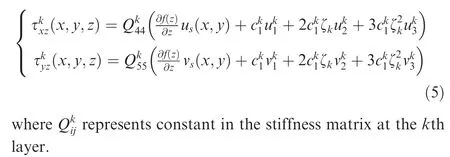
Applying the compatible conditions of transverse shear stresses between adjacent laminates, local parameters can be reduced. Finally, after transverse shear-free conditions on the upper and the lower surfaces of the plate will be utilized, a Sinusoidal-type Global-Local Theory (SGLHT) can be acquired, which can be expressed by

3. Finite element formulation based on the SGLHT

The proposed sinusoidal-type global-local theory possesses the second derivatives of transverse displacement parameter w in the formulation of strain energy. Therefore, Cdisplacement function satisfying the slope continuity is required.Nonetheless,it is a difficult issue that Ccompatible conditions can be fulfilled on the shared boundary between adjacent elements for a random mesh-configuration. For this reason, the definite expression of the Cdisplacement function is not shown in this study,while the second derivatives of transverse displacement can be shown by utilizing the functions of DKT element. In addition, the first derivatives of transverse displacement parameter w are also involved in the formulation of strain energy,so the shape functions of the BCIZ elementis utilized to discrete the transverse displacement. Therefore,displacement parameters of SGLHT within one triangular element can be denoted as

in which,b=y-y,c=x-x,and xand yrepresent the coordinates at the ith node.

In the light of the relationship between the displacement and the strain, the strain vector within an element can be denoted as

in which, land mrepresent the cosines of the vector normal to the ith edge, and Ssignifies length of the ith edge of element.

Displacement vector at the ith node can be denoted as follows

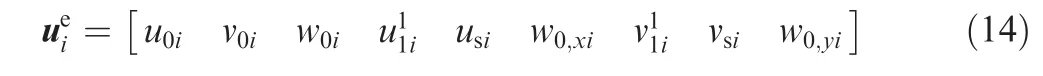
Once strain matrix in the Eq. (9) is presented, the element stiffness matrix kcan be acquired by utilizing the following equation.

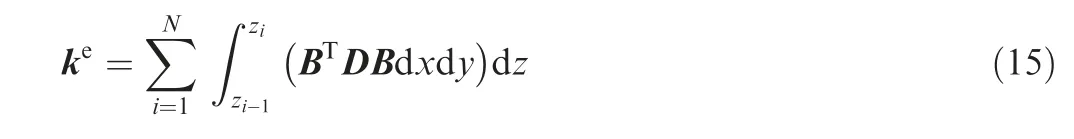
where D signifies a matrix made up of material constants at the ith ply.

Equation of motion within an element may be presented by utilizing the Hamilton’s principle, which is denoted as

where two dots represent the second derivatives relative to time, and msignifies the mass matrix of an element, which is expressed by

The matrix P in Eq. (17) can be denoted as follows

in which ρsignifies the density at the kth ply.

Assembling contribution of the mass and stiffness matrices of all elements, the global dynamic equation of finite element can be denoted as

where m and k denote the global mass and stiffness matrix,respectively.

For a harmonic vibration, the general result on dynamic Eq. (21) can be expressed the following form

Result of Eq.(23)can produce the frequency ω and the corresponding modal vector by imposing different boundary conditions.

But what if I break my arm again? My five year-old daughter asked, her lower lip trembling. I knelt holding onto her bike and looked her right in the eyes. I knew how much she wanted to learn to ride. How often she felt left out when her friends pedaled1（） by our house. Yet ever since she d fallen off her bike and broken her arm, she d been afraid.

4. Experimental testing

4.1. Testing samples

This work aims at studying effect of hole diameter on natural frequencies of sandwich plates,so three sets of samples are utilized to measure natural frequencies of sandwich plates with a circular cutout, namely group A, group B and group C. It requires to be shown that diameters of round holes are d=5 mm,10 mm and 20 mm,respectively.In order to reduce testing error, each group contains four samples. Testing samples are manufactured by using the aluminum material, the Polymethacrylimide(PMI)foam and the epoxy resin structural adhesive, which can be seen in Fig. 2. For face sheets of aluminum, thickness is 1.0 mm. Thicknesses of the core made of PMI foam is 6.0 mm. The length and the width of all samples are 284 mm and 40 mm, respectively, which are presented in Fig. 3. Young modulus, Poisson ratio and density of the used aluminum are 71 GPa, 0.3, and 2700 kg/m, respectively. For used PMI, Young modulus, Poisson ratio and density are 92 MPa, 0.375 and 75 kg/m, respectively.

4.2. Testing procedure

Fig. 2 Components of testing sample.

Fig. 3 Experimental testing of a sample.

The experimental testing on the natural frequencies of sandwich plates with a central hole of different diameters has been carried out by the hammering method.The equipment for this testing includes LMS data acquisition instrument, power amplifier, electromagnetic vibrator, acceleration sensor, force sensor and hammer. The accelerometer utilizes the piezoelectric effect of certain substances such as quartz crystals, where the force is applied to the piezoelectric element by the mass changes accordingly as the acceleration sensors are vibrated.If the measured vibration frequency is much lower than the natural frequency of the accelerometer, the change of force is proportional to the measured acceleration.

Firstly,the experimental samples are placed horizontally on the connection table,and the left and right ends are fixed with pads and bolts. It should be noted that the pads should be flatly attached to the joints at both ends of the samples, and no gaps or angles should be left.The experimental testing process is shown in Fig. 3. Then, the accelerometer is placed on one end of the samples. Finally, the other end of the testing sample is lightly knocked with a hammer.

The frequency response functions are extracted by modal testing and analysis software LMS Test, which are shown in Figs. 4-6. The abscissa value corresponding to the first peak of frequency response functions signifies the first-order natural frequency of the samples.The natural frequencies for the latter modes are obtained from the subsequent peaks,so the natural frequencies of all samples in three groups can be completely measured. Finally, the average value of the testing results of the four samples in each group can be acquired.

5. Numerical examples

To evaluate the performance of the proposed model,free vibration of a sandwich plate strip with one hole is firstly investigated by using the proposed model and 3D finite element model.Moreover, the three groups of sandwich plate strips including one hole with different diameters have been tested, which are utilized to assess the accuracy of the proposed method.Subsequently,impact of aperture on natural frequencies of sandwich square plates is investigated in detail. The results of the proposed model are also compared to those acquired from the chosen higher-order model and 3D finite element model.

5.1. Free vibration of a three-ply sandwich plate strip with one hole of different diameters is analyzed, which will be compared with testing data

Three groups of testing specimens with different hole diameters are applied to test natural frequencies of the sandwich plate.Testing specimens are made up of aluminum face sheets,PMI foam core and the epoxy resin structural adhesive,which has depicted in Fig. 2. Geometry of all specimens has been given in Section 4.1.The frequency response functions of three groups of specimens are shown in Figs.4-6.From the figures,the natural frequencies of all samples are obtained, which are shown in Tables 1-3.

The numerical examples of the free vibration analysis are performed by utilizing the finite element method. A typical finite element mesh division applied in numerical examples is shown in Fig. 7. Using 3D-FEM and finite element formulations established in the previous section, the natural frequencies of a sandwich plate strip having one hole of different diameters are computed and compared in Tables 1-3.

Comparisons of the numerical results obtained from the proposed model and 3D-FEM with the testing data in group A are presented in Table 1. The measured frequencies match well with the 3D-FEM results, which shows that the testing data are reliable. It can be noticed that the natural frequency values of the proposed model are close to the average values of the experimental data. Comparisons of the results corresponding to group B and group C are presented in Tables 2 and 3, respectively. Similarly, it can be readily observed that the SGLHT results agree quite well with the testing data.Thus,the present model has been validated accurately. It is noted that the SGLHT requires less computational cost than the 3D-FEM,which has a significant impact on the dynamic analysis requiring large number of elements.

The effect of a central hole of different diameters on free vibration behavior of sandwich square plates is investigated by using the testing data and numerical results. The experimental and numerical frequencies corresponding to the first four displacement modes of the sandwich plate with d = 5 mm, 10 mm and 20 mm holes are presented in Tables 1-3, respectively. It may be shown that the first four natural frequencies are subjected to very slight variations as the hole diameter is varied from 5 mm to 20 mm. However, it is possible that the results are not sensitive to changes in the diameter of centric hole because the length-to-hole diameter ratio (a/d)is relatively high and only the first four natural frequencies are measured.Therefore,the impact of aperture on natural frequencies of sandwich plates needs to be further investigated.

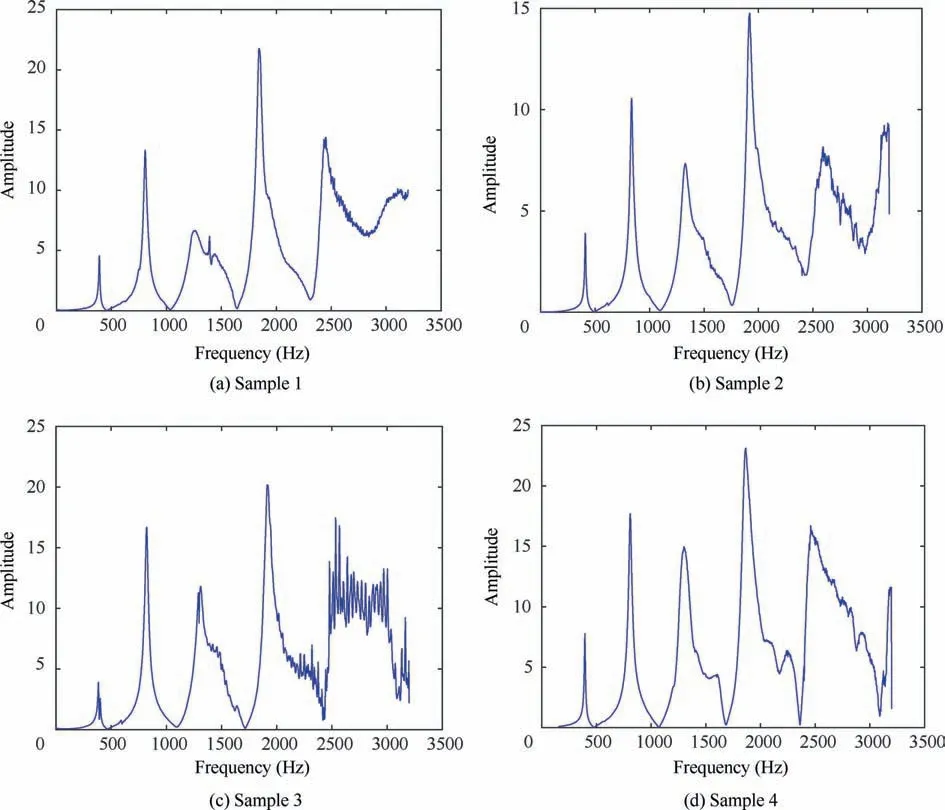
Fig. 4 Frequency response functions of samples in group A.

5.2. Impact of aperture on natural frequencies of sandwich square plates is deeply studied

Firstly,free vibration of a moderately thick sandwich plate(a/h=40,t/t=8)without holes with four Simply-Supported edges(SSSS)is studied,where tand tsignify the thickness of the core and the face sheet, respectively. The results acquired from various models have been presented in Table 4, where m and n are number of half waves along the x and y directions,respectively. It needs to be indicated that the higher-order models ED30 and ED54 in the article presented by Carrerahave been selected for comparison. The analytical results acquired from the models SGLHT, SPT, ED30and ED54have been compared with 3D-FEM results in Table 4.It can be noted that the maximum percentage error of results acquired from the SGLHT relative to 3D-FEM results is less than 5%, while the maximum percentage error of results acquired from the ED30 relative to 3D-FEM results is more than 90%. By increasing the order number of displacement components, the maximum percentage error of results acquired from the ED54 relative to 3D-FEM results is reduced to 12.97%. It needs to be shown that the model SGLHT contains seven independent displacement variables. However, the models ED30 and ED54 contain nine and seventeen displacement variables, respectively. Subsequently, free vibration of a moderately thick sandwich plate (a/h = 40, SSSS) containing a circular hole is investigated by using the present model SGLHT and 3D finite element model. The modal shapes are obtained and compared in Fig. 8. The corresponding normalized frequencies are also demonstrated in Table 5. It can be seen that the SGLHT results are in good agreement with the results obtained from the 3D-FEM. In addition, three higher-order plate models, namely SPT,THSDTand SHSDThave also been chosen for the comparison and these results are plotted in Fig.9(a).It is clear that unlike the model SGLHT,the chosen higher-order models overestimate the values of frequencies.

Fig. 5 Frequency response functions of samples in group B.

Using various models, a thick sandwich plate (a/h = 8)with four simply-supported boundaries (SSSS) is investigated for different length-to-hole diameter ratios. The natural frequencies for a/d = 10, 5 and 2.5 are presented respectively in Tables 6-8, and these results are plotted in Fig. 9(b)-(d),respectively. First fifteen displacement modes of the sandwich plate with a central hole of different diameters obtained from 3D-FEM and the model SGLHT are shown in Figs. 10-12. It can be observed that the results of the proposed model SGLHT are good enough for prediction of the dynamic response of the sandwich plates with different apertures,whereas the models SPT, THSDT and SHSDT significantly overpredict the natural frequencies of such structures for the same mesh size.Furthermore,the selected higher-order models have no capability to produce the natural frequencies corresponding to some higher displacement modes,such as the12th and 13th modes in the numerical example of a/d=10.Therefore, the first fifteen natural frequencies for the models SPT,THSDT and SHSDT cannot be given completely in Tables 6-8.In order to explain such abnormal phenomenon,displacement modes of the sandwich plate with a hole (a/h = 8, a/d = 2.5) obtained from the model SPTare plotted in Fig. 12(c). It may be observed that first eighth displacement modes of the model SPT are nearly the same as those acquired from the models SGLHT and 3D-FEM. Nevertheless, graphs from the ninth and the fifteenth displacement modes acquired from the model SPT are different from those obtained from the models SGLHT and 3D-FEM. Moreover, the same phenomenon is also encountered by the models THSDTand SHSDT. In general, natural frequencies are identified from the corresponding displacement modes.Therefore,this is inappropriate to compare natural frequencies obtained from different displacement modes, so that some frequencies acquired from the models SPT,THSDTand SHSDTare not presented in Tables 6-8. It requires to be indicated that natural frequencies of moderately thick plate (a/h = 40) have been completely calculated by using the models SPT,THSDTand SHSDT,which are shown in Table 5.Therefore,for free vibration analysis of thick sandwich plates, the compatible conditions of transverse shear stresses at the interfaces should be considered.Otherwise,it is hard to completely produce natural frequencies of thick sandwich plates attributing to the large change of transverse shear deformation at the adjacent layers of thick sandwich plates.f

Fig. 6 Frequency response functions of samples in group C.

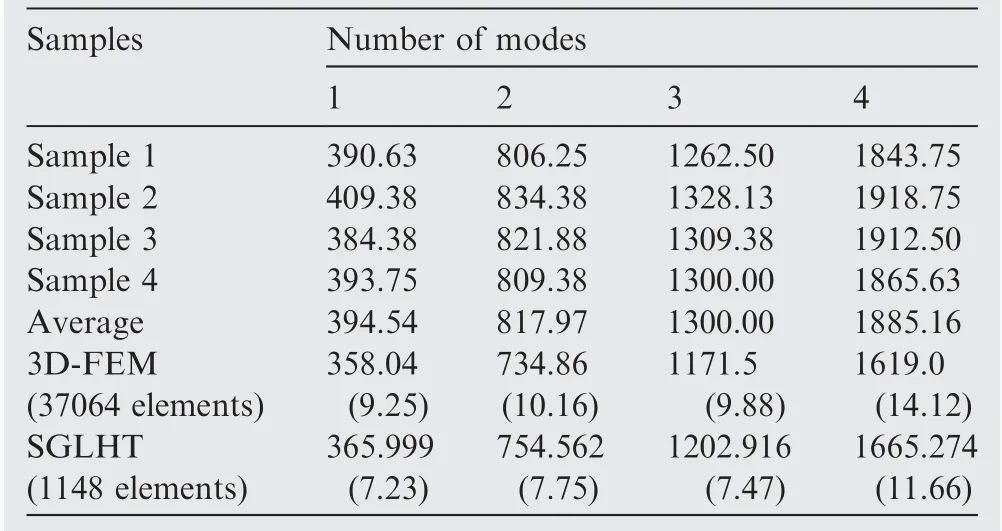
Table 1 Natural frequencies of the sandwich plates strips with one hole in group A (a = 284 mm, d = 5 mm).

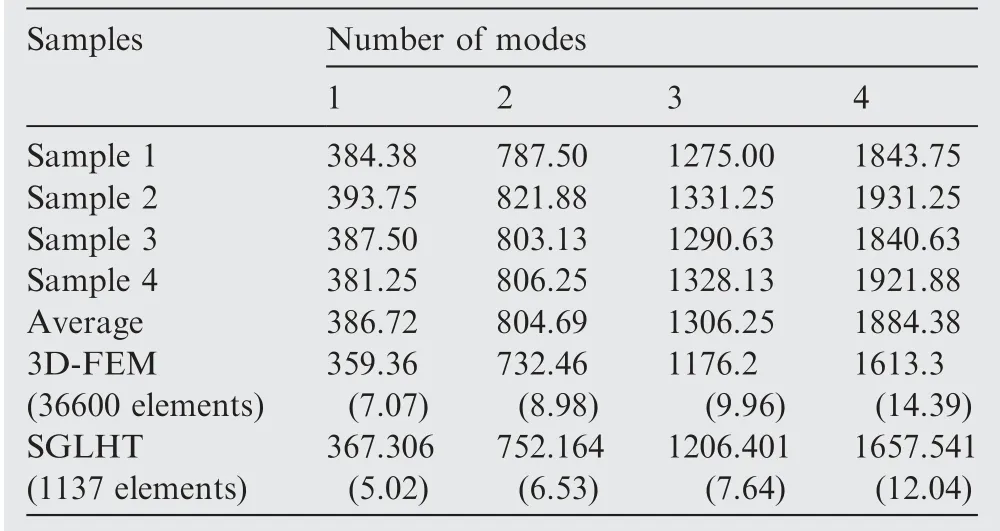
Table 2 Natural frequencies of the sandwich plates strips with one hole in group B (a = 284 mm, d = 10 mm).

In addition, effects of hole diameter on dynamic responses of sandwich plates with one hole under four simply-supported boundary conditions are further studied by investigating thevariations of natural frequencies. Various diameters of central hole corresponding to a/d = 10, a/d = 5 and a/d = 2.5 are investigated while other parameters remain constant. The frequency variations for different hole diameters of 3D-FEM and the present model SGLHT are depicted in Fig. 13. It can be observed that there are no uniform variations of frequencies for all modes with increasing hole diameter. For an example,as the diameter of the hole increases, the frequencies from the second mode to the fifth mode decrease slightly while the frequency for the sixth mode increases monotonically. On the other hand, the frequencies for higher modes may not always change monotonically. In Fig. 13, it is also noted that the decrease of a/d from 10 to 2.5 will increase first, and then decrease the natural frequencies of the thirteenth displacement mode. Moreover, it can be found that there are no considerable changes in natural frequencies corresponding to all modes as a/d decreases from 10 to 5.Nevertheless,as a/d is reduced to

2.5,similar phenomenon could not be found.There are significant variations in natural frequencies for the higher displacement modes of sandwich plates with one hole. It may be concluded that impact of aperture on the natural frequencies corresponding to the higher-order modes becomes more apparent by considering lower length-to-hole diameter ratio.Hence,in order to better understand and suggest the engineering structural applications, it is essential to accurately predict the dynamic response of sandwich plates with apertures.

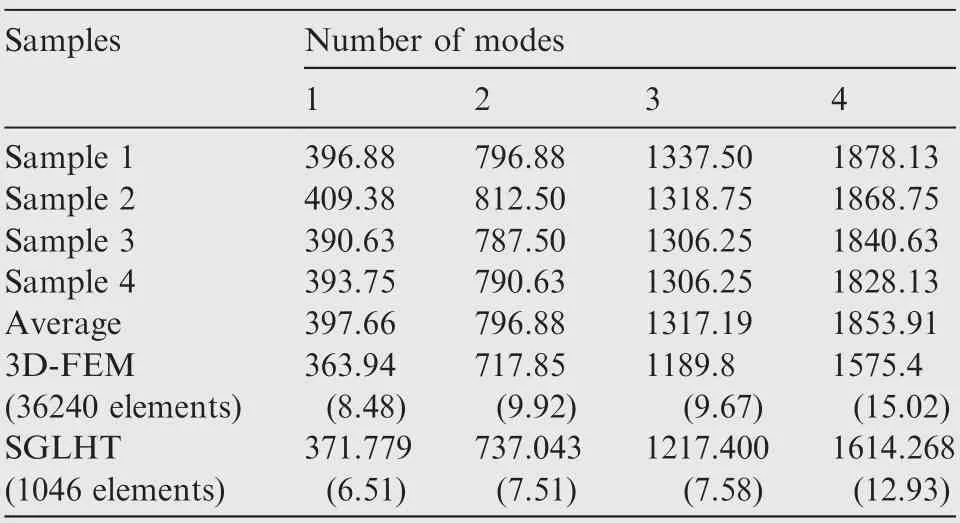
Table 3 Natural frequencies of the sandwich plates strips with one hole in group C (a = 284 mm, d = 20 mm).

Fig. 7 Finite element mesh configuration with 1137 meshes.

Fig. 8 Displacement modes obtained from 3D FEM and the model SGLHT (SSSS, tc/tf = 8, a/h = 40, a/d = 5).

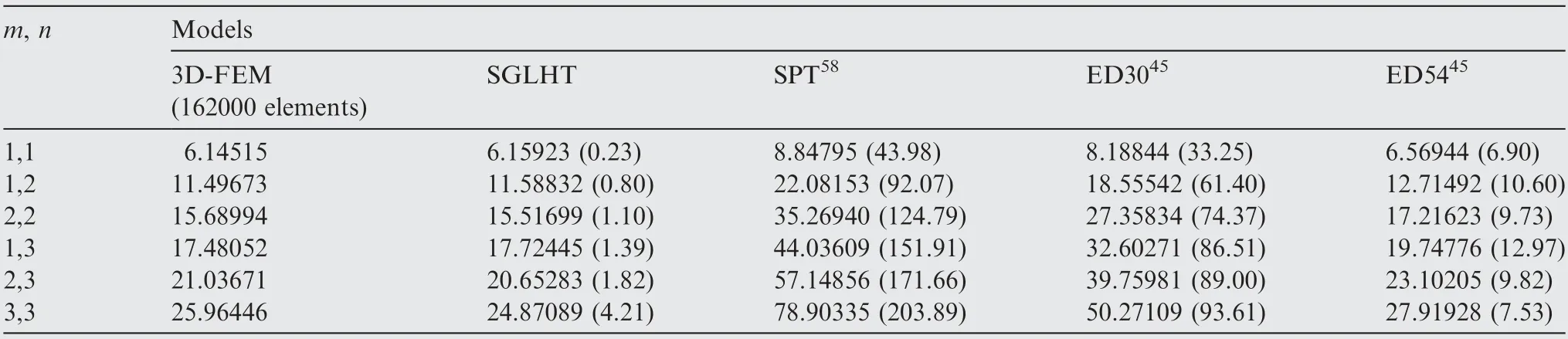
Table 4 Contrast of natural frequencies for three-ply sandwich plates without holes with four simply-supported boundaries (SSSS,tc/tf = 8, a/h = 40).

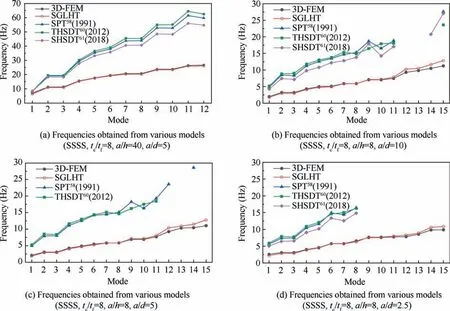
Fig. 9 Comparison of natural frequencies of sandwich plates with one hole obtained from various models.

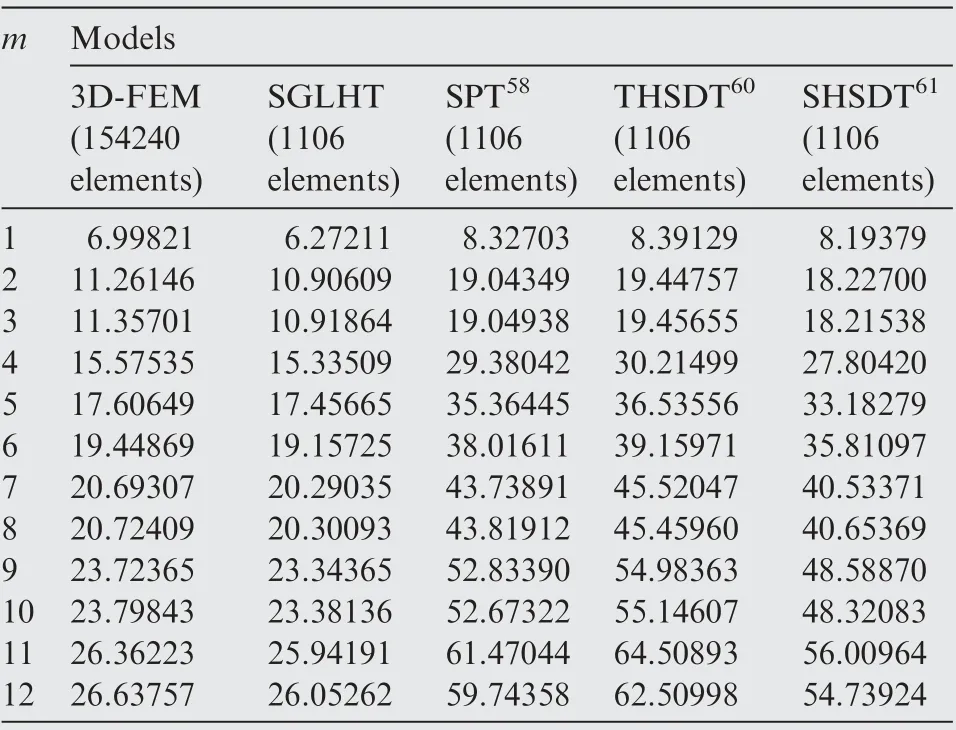
Table 5 Contrast of natural frequencies for three-ply sandwich plates containing one hole with four simply-supported boundaries (SSSS, tc/tf = 8, a/h = 40, a/d = 5).

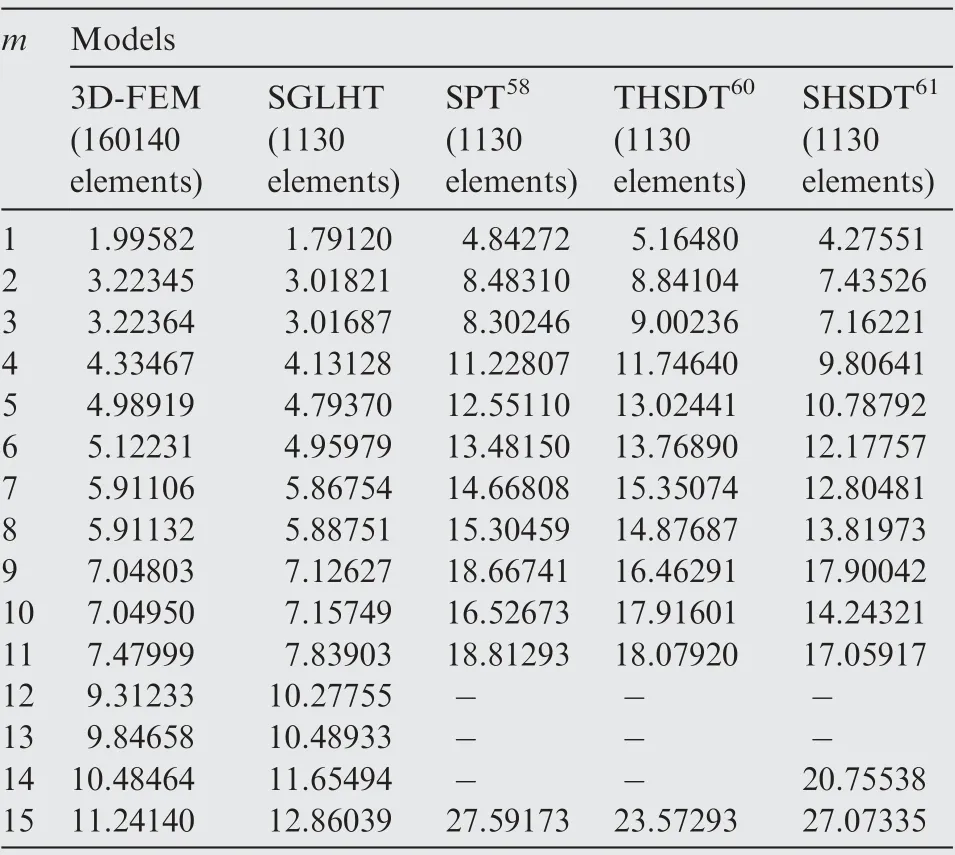
Table 6 Contrast of natural frequencies for three-ply sandwich plates containing one hole with four simply-supported boundaries (SSSS, tc/tf = 8, a/h = 8, a/d = 10).

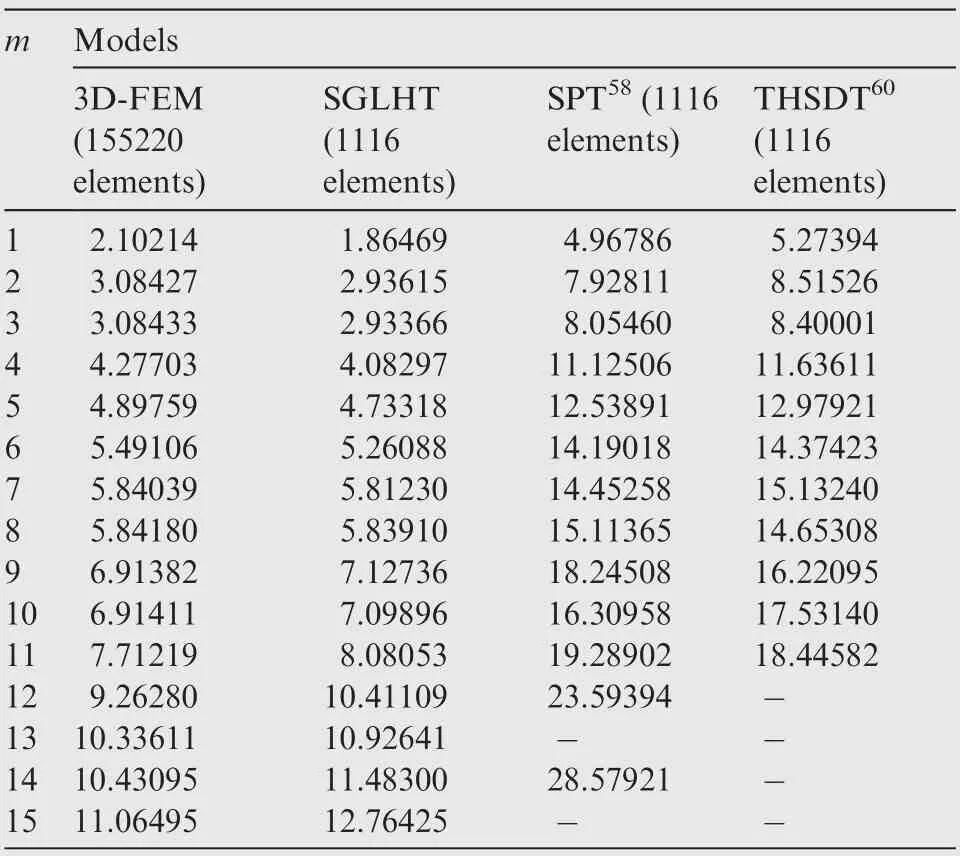
Table 7 Contrast of natural frequencies for three-ply sandwich plates containing one hole with four simply-supported boundaries (SSSS, tc/tf = 8, a/h = 8, a/d = 5).

Fig.10 Displacement modes obtained from(a)3D FEM and(b)the model SGLHT (SSSS, tc/tf = 8, a/h = 8, a/d = 10).

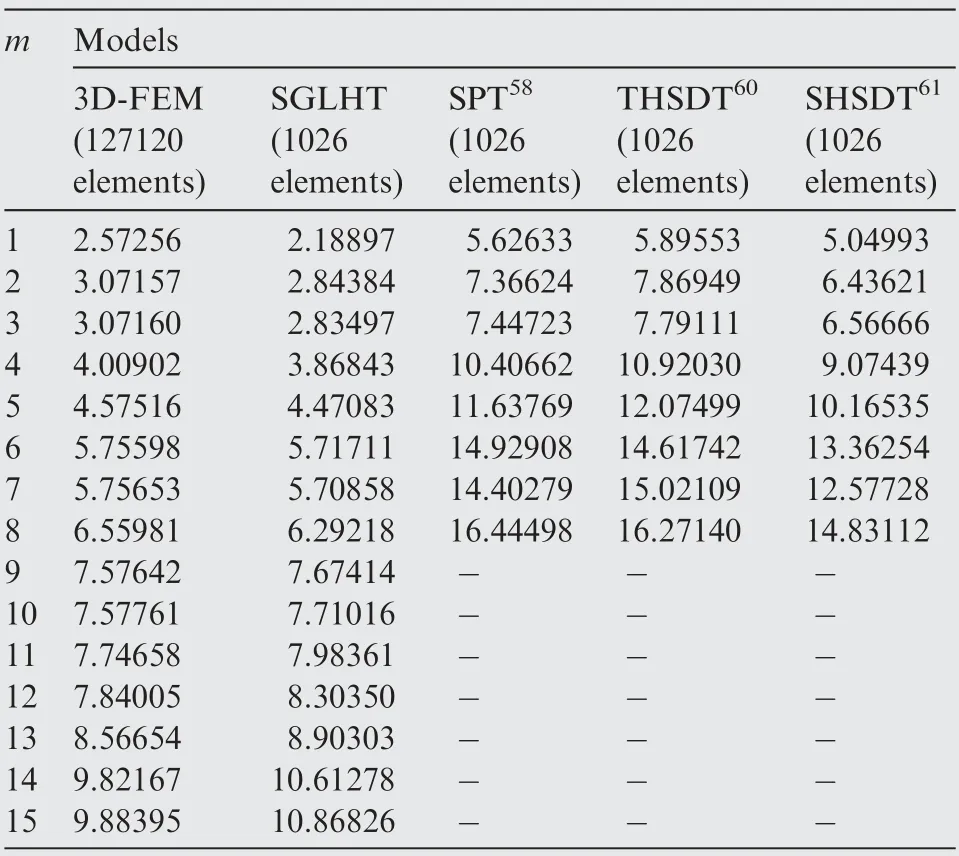
Table 8 Contrast of natural frequencies for three-ply sandwich plates containing one hole with four simply-supported boundaries (SSSS, tc/tf = 8, a/h = 8, a/d = 2.5).

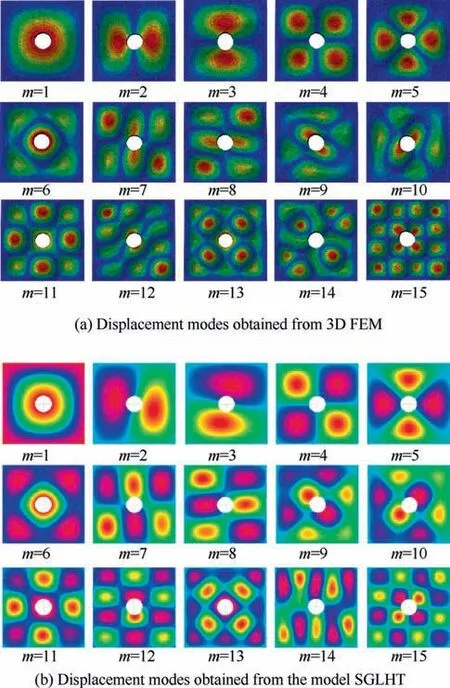
Fig.11 Displacement modes obtained from(a)3D FEM and(b)the model SGLHT (SSSS, tc/tf = 8, a/h = 8, a/d = 5).

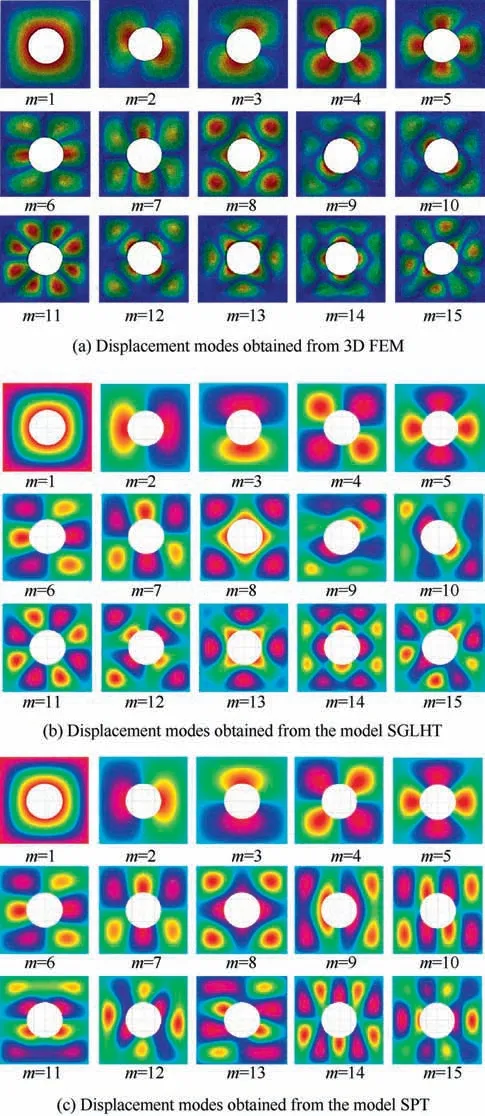
Fig.12 Displacement modes obtained from(a)3D FEM,(b)the model SGLHT and(c)the model SPT(SSSS,tc/tf=8,a/h=8,a/d = 2.5).

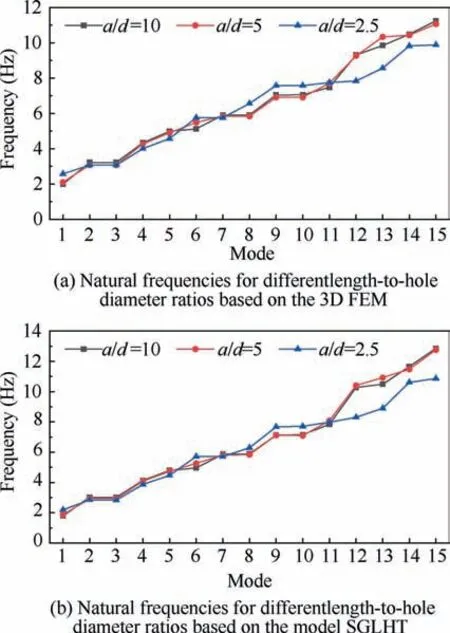
Fig.13 Natural frequencies of the sandwich plates with one hole for different length-to-hole diameter ratios based on 3D FEM and the model SGLHT.

6. Conclusions

In this paper, a sinusoidal global-local higher-order theory(SGLHT) is proposed to accurately predict natural frequencies of the sandwich plates with a circular hole. Using the Hamilton’s principle, the governing equation of motion is derived. To satisfy the continuity condition on the common edges of elements, the shape functions of the DKT element are utilized to discretize the first derivatives of transverse displacement parameter. Detailed formulation of finite element method has been presented. The established model has been verified by using the testing data of sandwich plates with different central holes. Subsequently, in order to assess the accuracy and efficiency of the present model,the results acquired from several higher-order models and 3D-FEM results have been also utilized for comparison.Furthermore, the impact of apertures on natural frequencies of sandwich plates with four simply-supported boundaries is investigated. By analyzing several examples, the following conclusions can be drawn:

(1) The proposed model can satisfy beforehand the interlaminar continuity of transverse shear stresses, so natural frequencies acquired from the proposed model agree well with testing data and the 3D-FEM results.

(2) The chosen higher-order theories neglecting the interlaminar continuity of the transverse shear stresses will overestimate the natural frequencies of sandwich plates with hole, and these models are also hard to completely produce natural frequencies of thick sandwich plates corresponding to some higher-order displacement modes.

(3) The aperture has an important impact on the higherorder frequencies of sandwich plates,while the influence of aperture diameter on the first tenth frequencies is slight. Therefore, the higher-order frequencies of sandwich plates merely become more sensitive to the change of hole diameter.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The work described in this paper was supported by SKLLIM1902, and the Natural Science Foundation in Shaanxi Province, China (No. 2019JQ-909).