主动随机送风条件下大口径离轴三反光学系统的计算机辅助装调

罗 敬，王金鑫，2，鞠国浩，尤晨旭，刘奕辰，徐天晓，2，李成浩，姜成强，马铭泽，2，何 煦，张晓辉，董吉洪，徐抒岩*

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033；2.中国科学院大学，北京100049）

1 引 言

三反消像散光学系统具备宽光谱、大视场、高成像分辨率、易控制杂散光等特性，在对地遥感、天文观测中得到了广泛的应用［1］。JWST［2］、CSST［3-4］、Euclid［5］、HabEx［6］和WFIRST-A［7］等均属于三反消像散光学系统。离轴三反光学系统因孔径离轴或视场离轴实现了无中心遮拦，这有利于提高系统的光通量和点扩散函数（Point Spread Function，PSF）质量。然而，离轴系统的非旋转对称性却增加了装调难度，传统的定心装调方法不再适用，因此，光学装调成为研制离轴三反光学系统的主要难点之一［8-11］。

随着科学技术的发展，成像观测精度的要求越来越高，进而迫使高分辨率光学系统朝大口径、长焦距方向发展。哈勃望远镜主镜口径2.4 m，系统焦距达到57.6 m［12］，其继任者JWST的口径更是达到6.5 m，系统焦距为131.4 m［2］。不断增大的口径和焦距进一步增加了光学系统的装调难度。一方面，随着口径的增大和像质的提高，光学系统中各个镜体的装调公差要求更为严格；另一方面，目前大多数计算机辅助装调方案均将系统波像差作为主要的输入信息，其检测精度直接决定了系统装调的效率和质量［13］。然而，大口径、长焦距光路中气流扰动成为决定系统波前检测精度的关键因素，这会对光学装调造成重要影响。因此，抑制光学检测中的气流扰动具有重要意义。

Shi［14］和陈华等［15］理论分析了气流扰动对折射率空间分布的影响机理，建立了相应的数学模型，并计算了不同状态下气流对波前像差的影响。姜自波等［16］结合理论分析和实验测量，深入研究了气流扰动对单镜面形检测结果的影响。徐抒岩等［17］针对气流扰动下大口径光学系统在实验室环境下装调困难的难点，提出通过主动送风来抑制气流扰动对波前检测的影响，取得了较好的效果。本文在此基础上，进一步提出结合主动随机送风和动态干涉仪多次平均累加的装调方案，降低了对风扇阵列的要求，提高了方案的可靠性和可实施性。通过Fluent软件仿真和多次实验迭代，优化了风扇数量、位置、朝向和风速等风场设置，最终较好地抑制了气流扰动对大口径、长焦距光学系统波前检测的影响。最后，在主动随机送风条件下完成了一个0.5 m口径、6 m焦距离轴三反光学系统的装调，取得了良好的收敛效果和系统像质。

2 基本原理

基于灵敏度矩阵的计算机辅助装调是目前应用最广泛的装调方法，其基本原理是：小失调范围内系统各个视场的Zernike系数变化量与失调量之间近似满足线性关系［13］。其数学模型可以表示为：

其中：ΔX为系统各个维度的失调量；A为灵敏度矩阵；ΔF为各项波像差的变化量，通常用各个视场波像差的Zernike多项式拟合系数来表示。若灵敏度矩阵A为满秩矩阵，则式（1）存在唯一解，有：

即通过灵敏度矩阵的逆与各视场Zernike系数变化量的乘积便可得到失调量。然而，在离轴三反消像散光学系统中，次镜和三镜各个维度对系统波像差的影响并不是相互独立的。比如，次镜沿Y轴的偏心与次镜和三镜绕X轴的倾斜均存在补偿。这表明灵敏度矩阵A的各个列向量不是线性无关的，不能通过线性组合表示出同等维度空间内的任意列向量ΔF。因此，灵敏度矩阵A不是满秩，属于奇异矩阵，不存在严格的逆［18］。综 上，式（1）是 矛 盾 方 程 组，不 存 在 解析解。

在许多实际问题中，线性方程组往往都是不相容的，即方程组没有严格意义的解。在这种情况下，人们追求的目标是得到不相容方程组的最优解，即最小二乘解。对于一个失调的光学系统，输入更多的像差信息可以更加真实地反映出系统的失调情况，从而更有利于找到方程组的最优解。因此，通常的做法是增加方程的数目，即矩阵A的行数。这导致矩阵A不再是方阵，其行数大于列数。此时，式（1）变为一个超定方程。根据多元函数的极值理论及矩阵运算和求导规则，该超定方程的最小二乘解为［13，18］：

式（3）也被称为法方程或者正则方程。然而，该正则方程的求解依然存在缺陷，即其条件数通常很大。这是因为离轴三反消像散光学系统中失调维度多，且波像差与失调参数之间的函数关系十分复杂，次镜和三镜各个维度失调量之间存在较为严重的互相关［13，19］。若系统的灵敏度矩阵A与测量结果ΔF均不存在误差，通过式（2）可以解算得到正确的失调量。然而，在测量时不可避免地会存在测量误差，大条件数会导致解算结果极易受到测量误差的影响而出现大范围波动，使得解算的失调量失真［20］。

建立线性方程组：

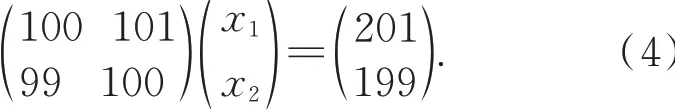
显然，该方程的精确解为X=(1 1)T。若右侧矢量存在微小的扰动，即：

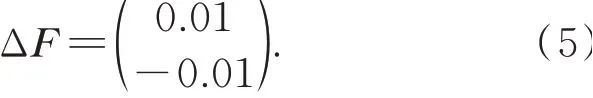
则式（4）变为：

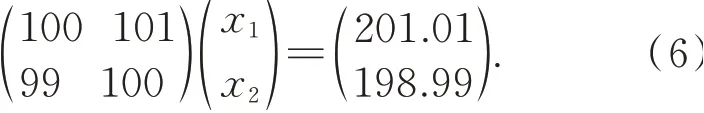
其解变为X=(3.01-0.99)T。尽管右侧矢量的扰动量很小，扰动前后方程的解却差异很大，若将扰动后的解作为最终结果会导致结果严重失真。

3 Zernike系数测量误差对计算机辅助装调的影响

输入参数测量误差会导致大条件数灵敏度矩阵的解出现大偏差。为了抑制大条件数灵敏度矩阵失调量解算结果随Zernike系数测量误差波动性大的问题，阻尼最小二乘法被提出［21］。尽管通过添加阻尼因子，可以有效减小灵敏度矩阵的条件数，避免失调量解算结果失真。然而，大的Zernike系数测量误差还是会降低装调结果的收敛效率，装调结果会随Zernike系数误差在一定范围内波动，导致次镜和三镜各个维度存在较大的装调残差。本文将基于一个0.5 m口径、6 m焦距的离轴三反光学系统，通过数值仿真来说明Zernike系数测量误差对计算机辅助装调的影响。

图1为离轴三反消像散系统光路，系统包含主镜、次镜和三镜，它们均为二次曲面。该系统焦距为6 m，入瞳直径为0.5 m，有效视场为1°×1°，各视场设计平均波像差RMS为0.05λ。本文分别计算了无Zernike系数误差、Zernike系数标准差σ=0.005以及σ=0.05三种情况下，次镜和三镜各个维度失调后经计算机辅助装调的收敛情况，每种情况下进行10组蒙特卡洛仿真计算。需要特别指出的是，三种情况下光学系统的初始失调量是以相同标准差随机生成的。当无Zernike系数测量误差时，装调前后系统各个视场的波像差如图2所示（彩图见期刊电子版）。显然，经计算机辅助装调后，各个视场的波像差回到了设计水平。次镜和三镜各个维度的装调残差均为0，如图3所示。

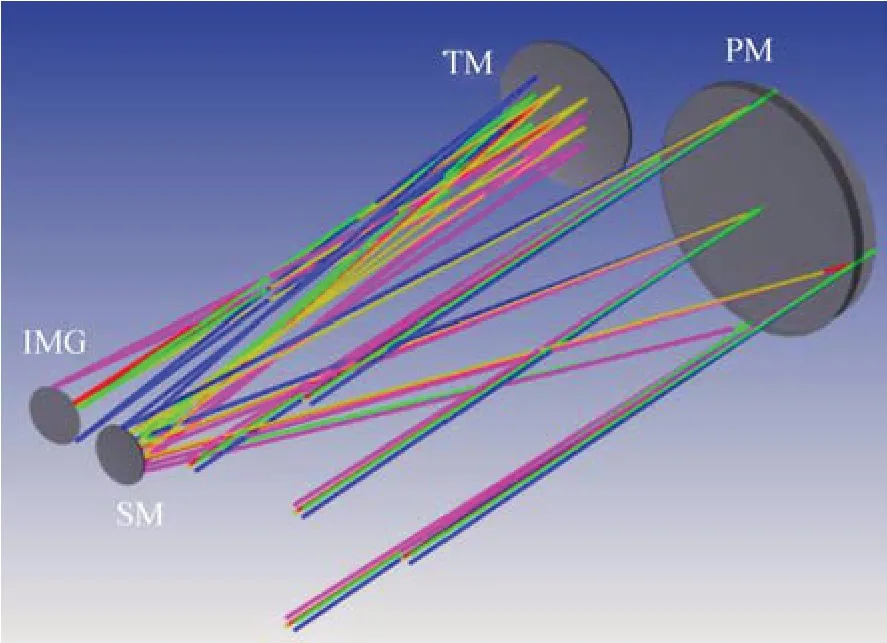
图1 离轴三反系统光路Fig.1 Optical layout of off-axis three-mirror anastigmat telescope

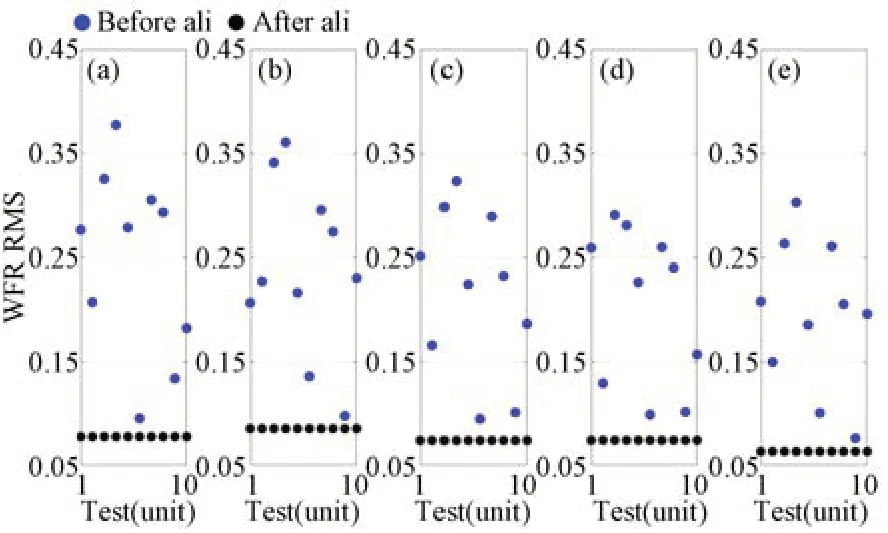
图2 无Zernike系数测量误差时装调前后光学系统各个视场的波像差RMSFig.2 Wavefront errors of optical system at different FOVs without measurement errors of Zernike coefficients

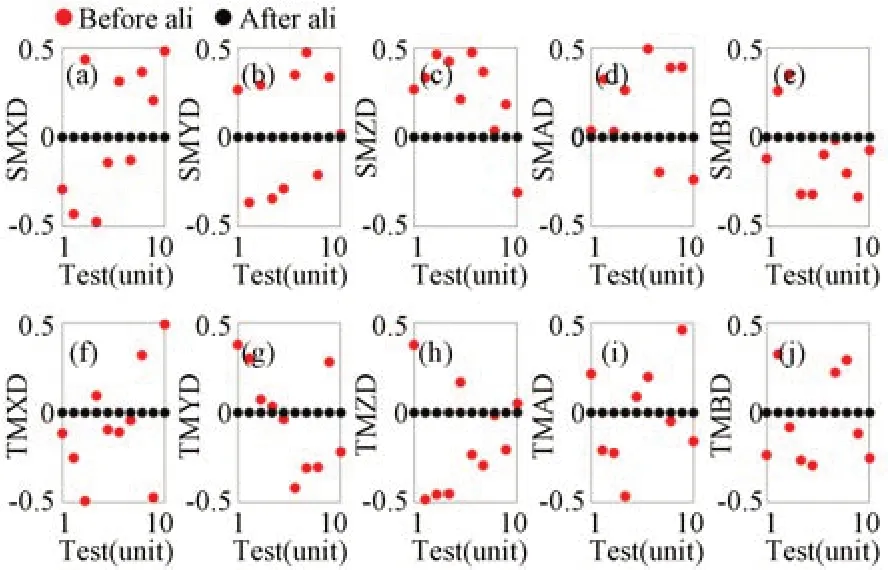
图3 无Zernike系数测量误差时装调前后次镜和三镜各个维度的残余失调量Fig.3 Misalignments of SM and TM without measurement errors of Zernike coefficients

当存在标准差σ=0.005的Zernike系数测量误差时，系统波像差和各维度失调量装调结果分别如图4和图5所示。可以看出，系统各个视场的波像差基本可以收敛到设计状态，但是相比较于图2，存在一定波动。次镜和三镜各个维度存在一定的装调残差，如图5所示，尤其是三镜沿Y轴偏心和绕X轴倾斜。将Zernike系数测量误差进一步增大，使其标准差σ=0.05，结果分别如图6和图7所示。显然，各个视场的波像差已很难收敛到设计状态，次镜和三镜的装调残差也明显变大。

图4 Zernike系数测量误差σ=0.005时装调前后光学系统各个视场的波像差RMSFig.4 Wavefront errors of optical system at different FOVs with measurement errors of Zernike coefficients with standard deviationσ=0.005

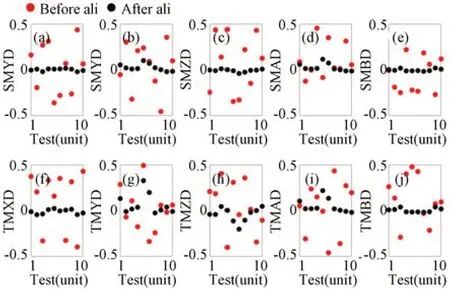
图5 Zernike系数测量误差σ=0.005时装调前后次镜和三镜各个维度的残余失调量Fig.5 Misalignments of SM and TM with measurement errors of Zernike coefficients with standard deviationσ=0.005

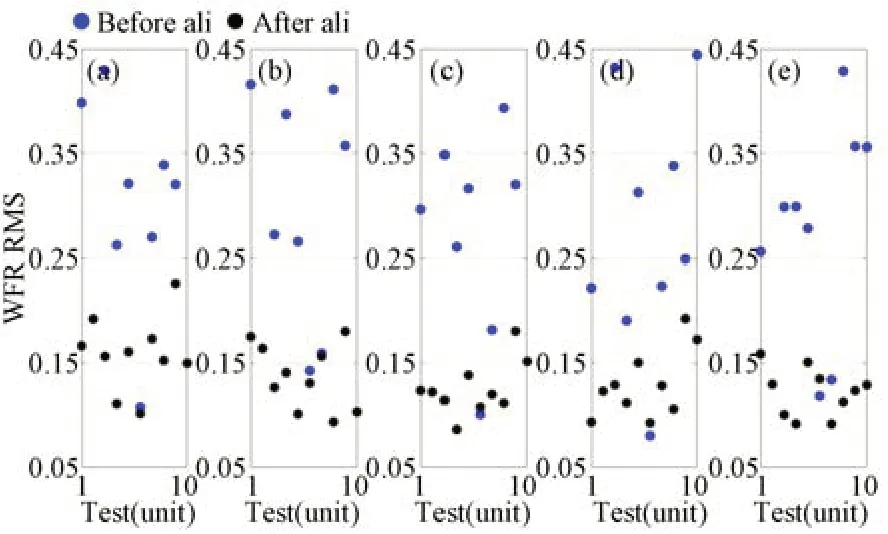
图6 Zernike系数测量误差σ=0.05时装调前后光学系统各个视场的波像差RMSFig.6 Wavefront errors of optical system at different FOVs with measurement errors of Zernike coefficients with standard deviationσ=0.05

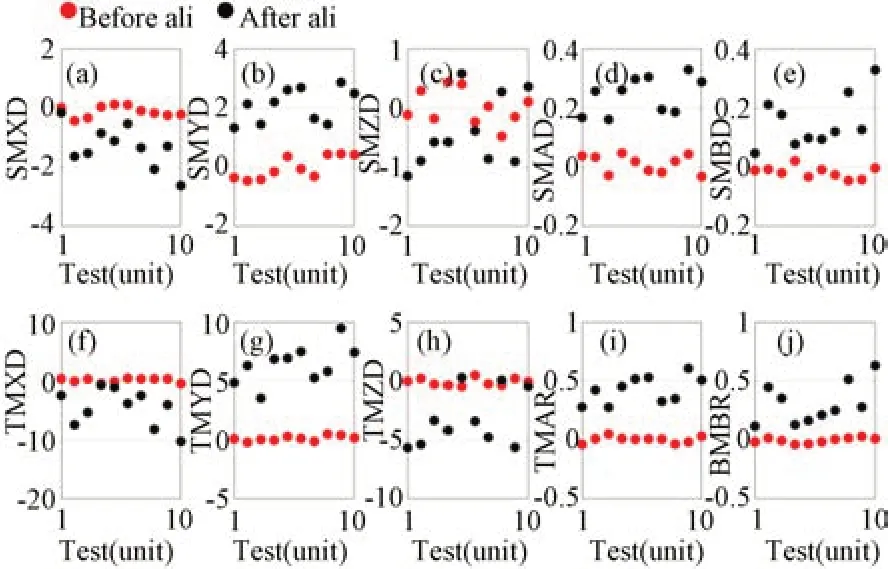
图7 Zernike系数测量误差σ=0.05时装调前后次镜和三镜各个维度的残余失调量Fig.7 Misalignments of the SM and TM with measurement errors of Zernike coefficients with standard deviationσ=0.05

上述仿真结果表明，基于波前检测的计算机辅助装调结果会受到Zernike系数测量误差的显著影响。Zernike系数测量误差过大，会导致离轴三反光学系统中次镜和三镜各个维度的装调残差增大，系统波像差的波动性变大，甚至无法收敛。

增大通光口径是光学系统提高成像分辨率的主要手段。随着口径的增大，气流扰动成为影响系统波前检测精度，进而影响系统装调效率和质量的关键因素。目前，不管是实验室极限温控，还是使用大型真空罐，均需要付出极大的经济和时间成本。针对上述问题，本文在基于主动送风的大型光学系统波前检测气流扰动抑制方案［17］的基础上，结合理论仿真和实验迭代，进一步优化了风场设置，将各个风扇的朝向随机化，彻底扰乱干涉检测光路中的折射率场，使它变成随机分布，并通过动态数字干涉仪的快速多次累加，得到了稳定的干涉检测结果。

4 主动随机送风条件下的Zernike系数测量

实验系统如图8所示，由一个6 m焦距、0.5 m有效通光口径的离轴三反消像散光学系统、两个六足调整台、自准直平面反射镜、干涉仪和风扇等组成。结合前期Fluent软件仿真结果，并经过多次实验迭代，更改风扇位置，将水平朝向［17］改为置于干涉光路的下方，进而采取由下往上的方式进行主动送风，并优化了风扇到系统光轴的间距。为扰乱整个光路的温度场和折射率场，需确保风扇阵列充满整个干涉检测光路，且所有风扇均摇头摆动，朝向角度随机，各个风扇之间的相对位姿也随机，最终使得干涉检测光路的气流随机分布。

图8 离轴三反系统自准直干涉检测光路Fig.8 Optical path for self-collimating interference detection of off-axis three mirror anastigmat telescope

为验证主动随机送风条件下大口径、长焦距光学系统波前检测数据的稳定性，通过动态干涉仪对光学系统波前进行多次累加测量。保持图8中所示光路不变，分别在风扇开启和风扇关闭两种条件下对系统波前进行测量，每种条件下各测得10组数据，每组数据均包含500次原始数据的累加。在上述两种条件下，干涉仪的数据采集模式、曝光时长、Mask大小，以及干涉仪、次镜和三镜调整台的位姿等均保持一致，且所有数据均在同一天测得。实验结果如图9所示，图中给出了Z5～Z16在不同环境条件下的稳定性。显然，图9（a）数据的稳性明显好于图9（b）。对两种环境条件下的数据进行统计计算，各项条纹Zernike系数的标准差如表1所示。在主动随机送风条件下，Z6～Z16的标准差在0.003以下，Z5的波动稍大，但也小于0.01。作为比较，关闭风扇后，保持光路其他元件、参数不变，Z5标准差增大了近4倍，达到0.037，其他各阶Zernike系数的稳定性也明显变差。上述数据充分证明，通过主动随机送风，可以有效抑制大口径、长焦距干涉检测光路的气流扰动，大幅度提高波前检测的稳定性。

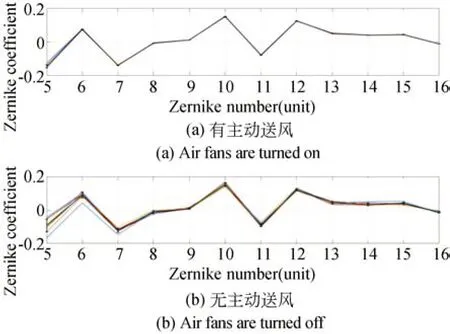
图9 不同条件下的自准直干涉光路波前检测结果稳定性Fig.9 Stability of wavefront measurement results of selfcollimating inteference optical system in different conditions

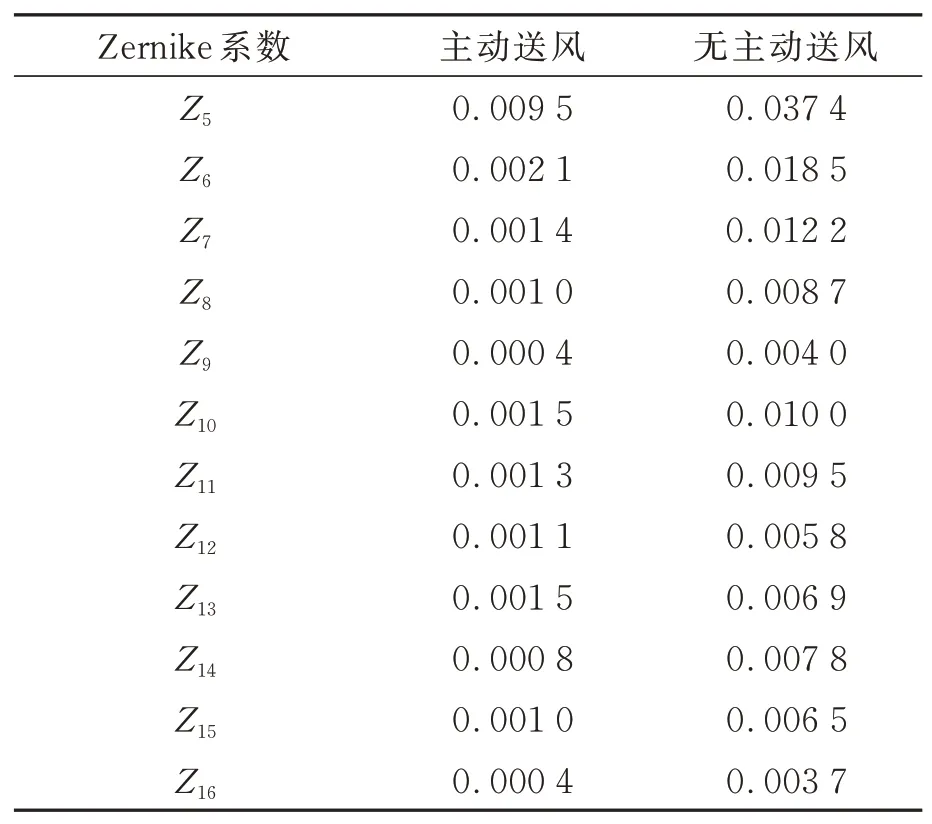
表1 不同测试条件下的条纹Zernike系数标准差Tab.1 Standard deviations of fringe Zernike coefficients under different measuring conditions

上述测试结果验证了数据的稳定性，还需要进一步验证数据的正确性。若上述波前检测结果是由风扇送风而额外生成的，那么波前数据必然和风扇的设置密切相关，尤其是风扇的位置和朝向。因此，人为地改变光路中的风扇朝向和位置，如图10所示，风扇阵列处于3种不同的组合状态。在这3种状态下，保持光路中其他参数和元件不变，采集系统波前数据，结果如图11所示。可以发现，尽管风扇阵列的设置发生了很大变化，但是3种情况下波前检测结果几乎没有区别，Z6和Z7的平均值也非常接近，如表2所示。图12给出了3种不同风扇阵列设置情况下Z5～Z36的变化情况，可以看出，所有的Zernike系数在不同的风扇设置下基本一致。上述实验结果表明，图9和表1所示的波前检测结果不随风扇设置的不同而变化，能够表征图8中自准直干涉检测光学系统的真实波前。

图10 干涉检测光路中三种不同的风扇组合Fig.10 Three different air fan combinations placed in inteference optical path

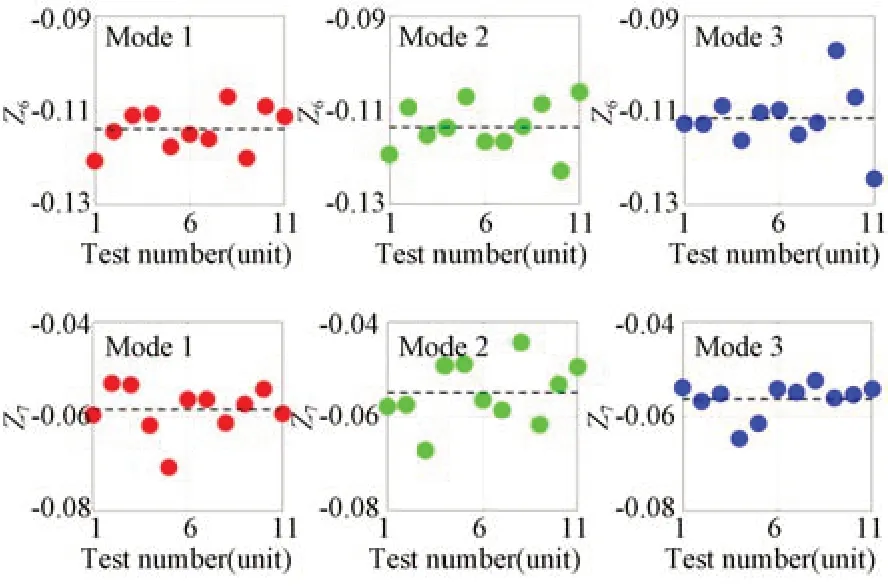
图11 三种不同风扇组合下Z6和Z7的检测结果Fig.11 Measured results of Z6 and Z7 under three different air fan combinations

表2 三种不同风扇组合下Z6和Z7的检测结果平均值Tab.2 Mean values of Z6 and Z 7 with three different air fan combinations

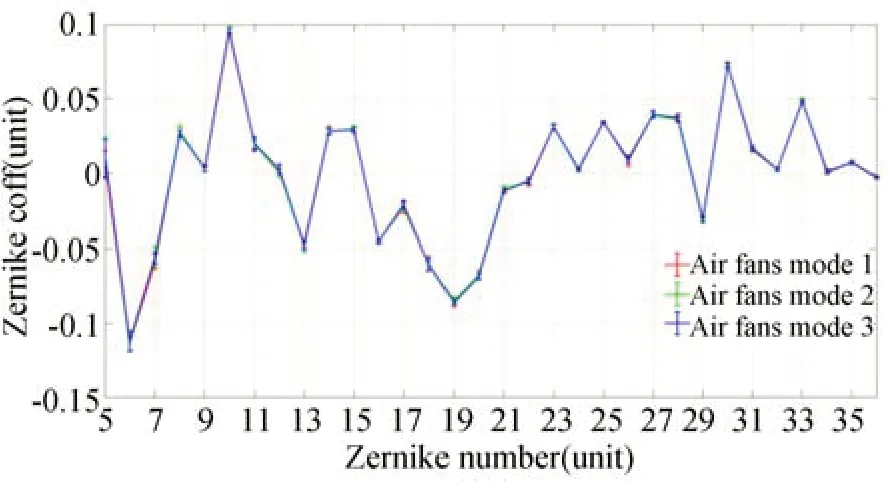
图12 三种不同风扇组合下Z5～Z 36的检测结果Fig.12 Measured results of Z5-Z 36 with three different air fan combinations

5 实验与结果

由实测数据可知，通过主动随机送风可以提高大口径、长焦距干涉光路波前检测结果的稳定性，并得到真实的系统波前结果。下面，我们将首次在主动随机送风条件下，完成该离轴三反光学系统的计算机辅助装调。

根据待装调光学系统的特点，通过经纬仪和激光跟踪仪完成系统粗装调。将干涉仪和自准直平面反射镜调整到位，经过一段时间连续主动随机送风后，开始采集系统各个视场的波前数据，并保持系统一直处于主动随机送风状态。根据待装调光学系统的视场离轴特点选定5个视场，包括4个边缘视场和1个中心视场，如图13所示。测得粗装调完成后系统各个视场的波像差，如图14所示。系统各视场波前RMS平均值为0.493λ。

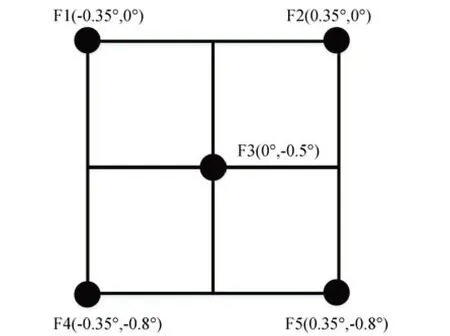
图13 计算机辅助装调相关的5个视场Fig.13 Five fields of views used in computer-aided alignment

图14 粗装调结束后离轴三反光学系统5个视场的波像差检测结果Fig.14 Measured wavefront errors over five different fields of views of off-axis TMA telescope after initial alignment

通过自编的计算机辅助装调程序，根据测得的各个视场的Zernike系数，解算得到次镜和三镜的失调量，再通过次镜和三镜底部的六足台调整次镜和三镜的位姿。调整完成后，再次检测各个视场的波像差，波前检测结果如图15所示。各视场波像差RMS平均值降为0.094λ。显然，系统各个视场的波像差明显收敛，表明失调量解算结果正确。根据该轮检测结果，又解算得到一组次镜和三镜的失调量，再次调整后，检测得到各个视场的波像差如图16所示，条纹Zernike系数如表3所示。各视场波像差RMS平均值进一步降为0.086λ，达到该系统的装调指标要求。

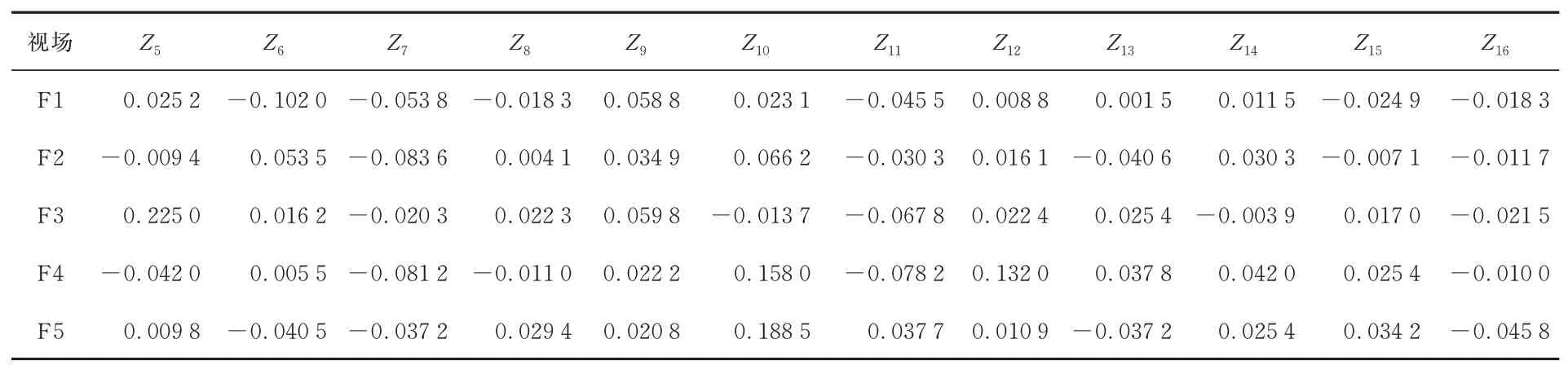
表3 两轮计算机辅助装调后系统各个视场条纹Zernike系数Tab.3 Measured fringe Zernike coefficients over five different fields of views of off-axis TMA telescope after second round CAA

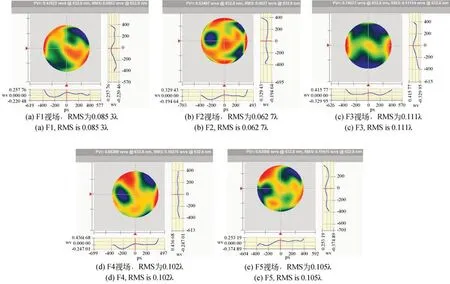
图15 第一轮计算机辅助装调后系统5个视场的波像差检测结果Fig.15 Measured wavefront errors over five different fields of views of off-axis T MA telescope after first round CAA

图16 第二轮计算机辅助装调后系统5个视场的波像差检测结果Fig.16 Measured wavefront errors over five different fields of views of off-axis TMA telescope after second round CAA

6 结 论

本文提出主动随机送风的方案来抑制气流扰动对大口径、长焦距干涉光路波前检测的影响。结合仿真结果和多次实验迭代，优化了风扇阵列的数量、位置、朝向和风速等风场设置，使得通过主动随机送风可以实现对大口径、长焦距干涉光路温度场和折射率场的扰动随机化。测试结果表明，通过主动随机送风可以显著提高系统波前检测结果的稳定性，Zernike系数标准差由0.04降低到0.01以下。最后，在主动随机送风条件下，对一个6 m焦距、0.5 m通光口径的离轴三反消像散光学系统进行了装调。实验结果显示，在稳定的Zernike系数检测结果下，通过一轮计算机辅助装调，系统各个视场的波像差RMS平均值由0.49λ降低到0.094λ；两轮装调后系统各视场波像差RMS平均值达到0.086λ，满足系统指标要求。由此表明，通过主动随机送风，可以以极低的成本为大口径、长焦距光学系统提供稳定、可靠的波前检测环境，这对于大口径光学系统的研制及应用具有重要意义。