基于分位数回归的大病医疗住院费用影响因素分析

刘 沛 钟仕洋 郭 威 吕奕鹏 汤元杰

1 海军军医大学卫生勤务学系数理教研室，200433 上海；2 武警江苏省总队医院门诊部，225003 江苏 扬州；3 海军军医大学卫生勤务学系统计学教研室，200433 上海；4 上海交通大学医学院社会医学与卫生事业管理系，200025 上海；5 武警江苏省总队医院，225003 江苏 扬州

《“健康中国2030”规划纲要》提出要进一步健全重特大疾病医疗保障机制，加强基本医疗保险、城乡居民大病保险、商业健康保险与医疗救助的有效衔接[1]。近年来，对于发生高额医疗费用的群体，国家也采取了多项举措给予补偿，减轻其经济负担，减少“因病致贫，因病返贫”。然而诸多研究显示：当前医疗保障制度的大病保障功能总体不强，没能从根本上化解大病患者的经济风险[2-4]。

此外，国内大多数针对住院费用影响因素的研究仍采用传统的线性回归模型，对于住院费用此类偏态分布的资料具有一定的局限性。因此本研究拟采用分位数回归模型探讨大病住院费用的影响因素，以期为合理控制大病住院费用提供理论依据。

1 资料与方法

1.1 资料来源

本研究选取江苏省扬州市某三级医院2016—2019年的住院诊疗数据，包括：社会人口学特征、身份类别、费用类别、入院时间、出院时间、有无手术、患者来源、入院医疗费用等22项指标。根据《扬州市区职工大病补充保险实施意见》[5]和《扬州市城乡居民基本医疗保险实施细则》[6]中的大病保险起付标准，选取住院医疗费用超过15 000元的患者，剔除信息不完全者，实际纳入样本共计10 060例。

1.2 研究方法

采用Excel 2010建立数据库，运用Stata 16.0统计软件对整理的数据进行单因素分析(Wilcoxon rank sum检验、Kruskal-WallisH检验)，以选择纳入模型中的变量。检验水准α=0.10。由于住院费用不符合正态分布，不满足线性回归的假设条件，因此，本研究采用分位数回归模型，选取住院费用的第10分位数(P10)、第50分位数(M)和第90分位数(P90)分析住院费用低、中、高水平下的影响因素。

1.3 分位数回归模型

分位数回归是计量经济学的研究前沿方向之一，最早由Roger Koenker和Gilbert Bassett于1978年提出。它利用解释变量的多个分位数来得到被解释变量条件分布的相应分位数方程。与传统的OLS(普通最小二乘法)只得到均值方程相比，分位数回归可以更详细地描述变量的统计分布。它是给定回归变量X，估计响应变量Y条件分位数的一个基本方法；它不仅可以度量回归变量在分布中心的影响，还可以度量在分布上尾和下尾的影响，因此比最小二乘回归更具优势，估计结果也更为稳健[7-8]。分位数回归模型原理如下所述。

定义随机变量Y的分布函数为

F(y)=P(Y≤y)

定义随机变量Y的τ分位数函数Q(τ)为

Q(τ)=inf{y:F(y)≥τ}

其中，0<τ<1代表在回归线或回归平面以下的数据占全体数据的百分比。分位函数的特点是：被解释变量y的分布中存在比例为τ的部分小于分位数函数Q(τ)，而(1-τ)的部分大于分位数函数Q(τ)。

为了对分位数回归求解[9-11]，首先定义概率函数

其中，u为反映概率密度函数的参数；ρτ(u)表示被解释变量y的样本点处于τ分位以下和τ分位以上时的概率密度函数关系。假设分位数回归模型为

最小二乘回归的目标是使误差平方和最小，即

而分位数回归是寻求y在Q分位数下的绝对离差和最小，即

为简单起见，在具体估计过程中可以假设u=1，则对于任何一个τ分位数回归而言，参数估计就是要使加权误差绝对值平方和最小：

其中，Yi为被解释变量的向量；Xi为解释变量的向量；τ表示估计的分位数值。

当τ在(0,1)上取不同的值时，就可以得到不同的参数估计值[10-12]。运用分位数回归模型，可以分析不同住院费用所处位置，住院费用如何受各个变量的影响。本文建立如下计量模型：

YQi=β0Qi+β1QiXi+…+βnQiXn

其中，β0Qi代表分位数为Qi时回归方程的常数项；β1Qi,β2Qi,…,βnQi分别代表当分位数为Qi时回归方程X1,X2,…,Xn的系数[13]。

2 结果

2.1 基本情况

经分析发现，4年间大病患者住院费用中占比最高的为材料费(32.42%)，其次为药品费(28.49%)，第3为治疗费(15.31%)。纵向对比来看，药费占比从2016年的33.79%，下降到2019年的24.85%，下降了8.94百分点。见表1。

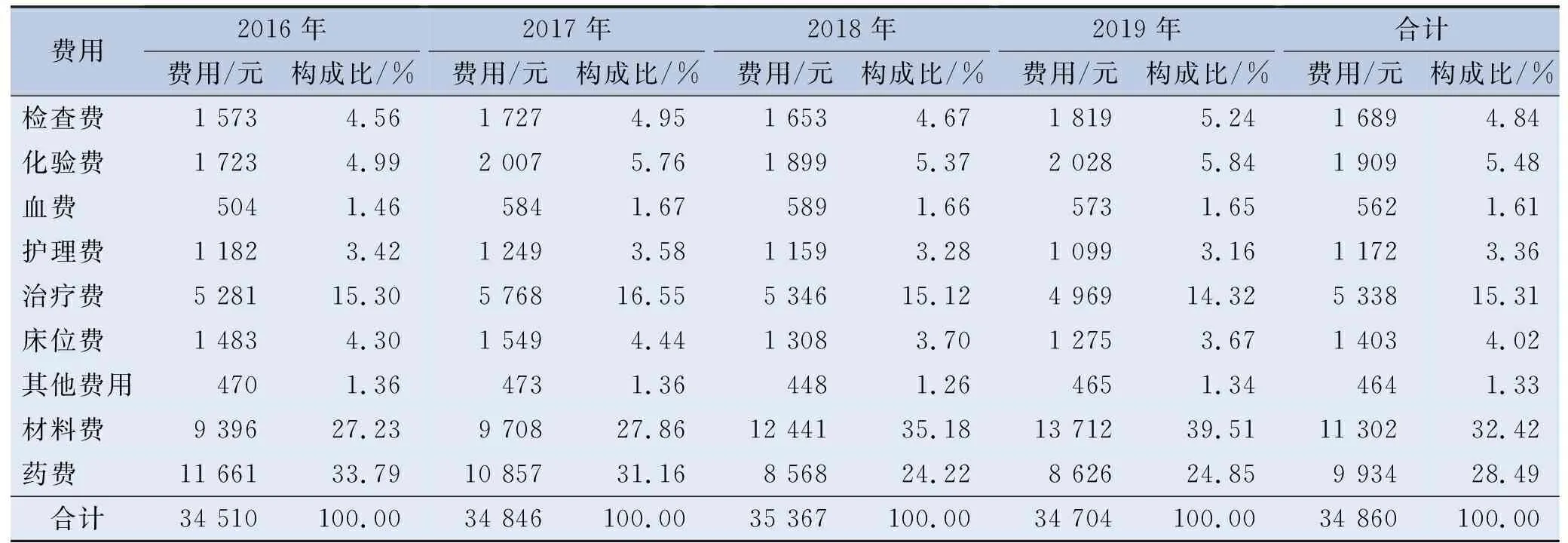
表1 参保大病患者次均住院费用及构成比

2.2 住院费用的单因素分析

单因素分析结果显示年龄、婚姻状况、患者来源、人员身份、付费方式、住院天数、手术、治疗效果、住院次数9个因素各层间的住院费用差异有统计学意义(P<0.10)。见表2。

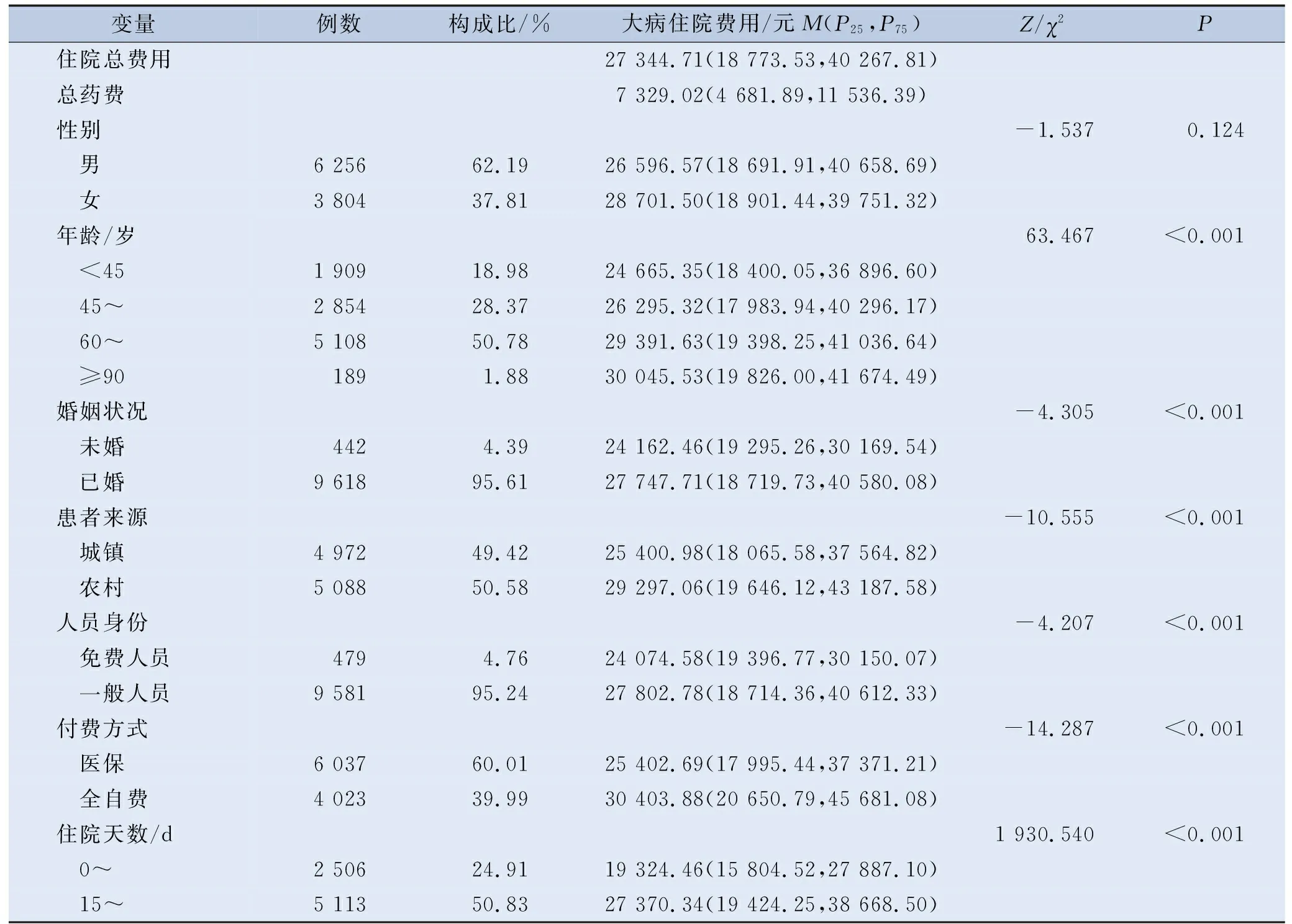
表2 住院费用单因素分析结果

2.3 大病患者住院费用的分位数回归分析

基于单因素分析结果，选择年龄、婚姻状况、患者来源、人员身份、付费方式、住院天数、手术、治疗效果、入院次数作为解释变量纳入模型，采用分位数回归模型分析不同大病患者住院费用的影响因素。由于本研究更关注极高费用和极低费用患者的影响因素，因此选取分位数P10、M、P90。

患者付费方式、住院天数、有无手术、入院次数4个因素分位点上对住院费用的影响均有统计学意义(P<0.05)。且付费方式、住院天数和有无手术3个因素在住院费用的高分位点上的影响强度高于低分位点。入院次数越多住院费用越少，且在50%分位点上的影响强度高于其他2个分位点，年龄因素中60～<90岁的患者各分位点上均高于45岁以下患者(P<0.05)。诊疗效果因素中，治愈患者各分位点上的住院费用低于未愈或死亡患者(P<0.05)。见表3。

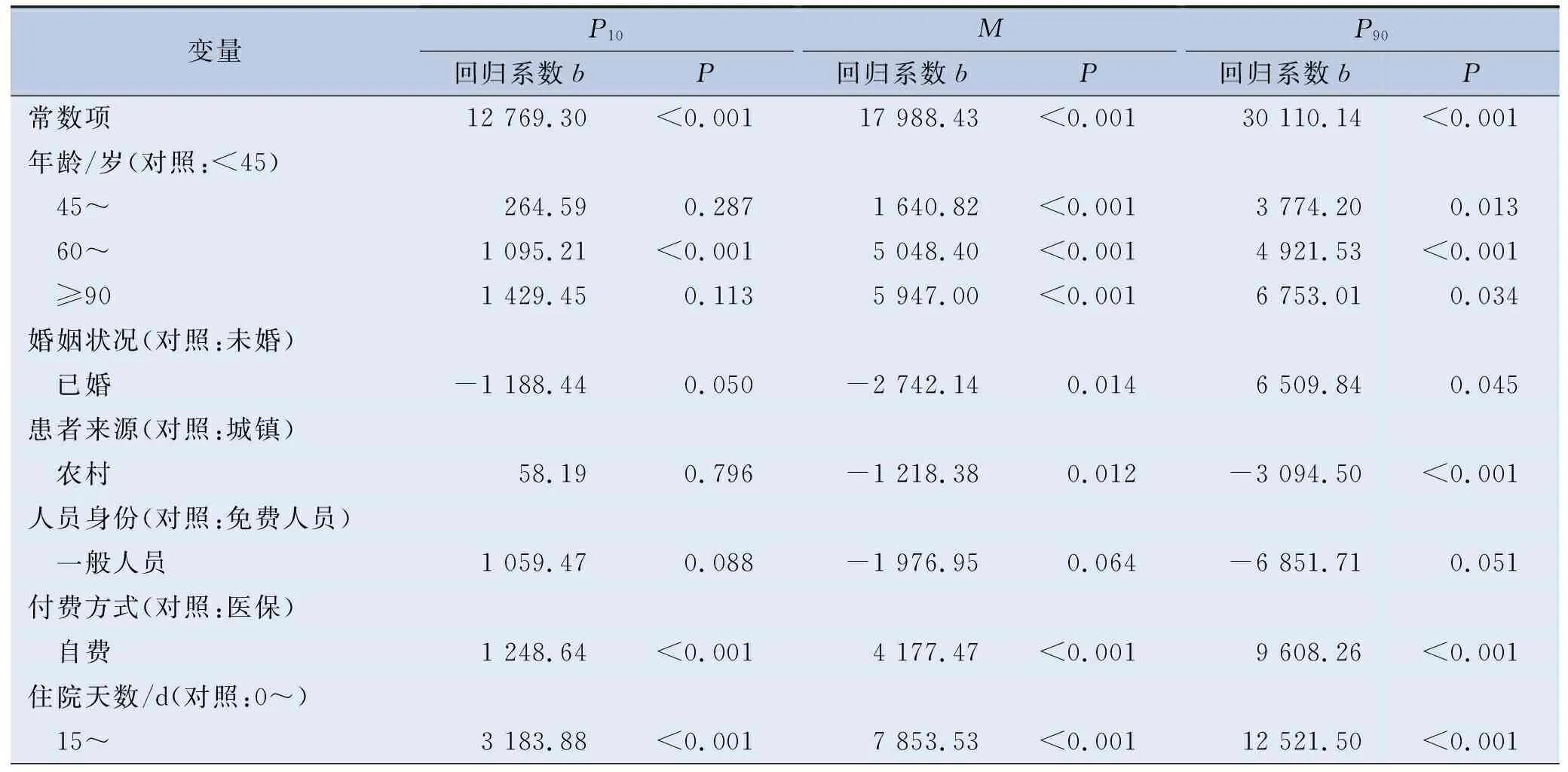
表3 大病患者住院费用影响因素分位数回归模型估计结果

3 讨论

3.1 药费占比逐渐降低，低于国家平均水平

从住院费用的构成发现，药费占比逐年下降，4年间从33.79%下降到24.85%，下降了8.94百分点，且低于全国同期平均水平(27.50%)[14]。这表明随着江苏省“取消药品加成”方案的不断推进，政策实施效果逐步显现，广大人民群众“看病贵”难题有效缓解。

此外，还应注意到，4年间材料费上涨超过12百分点。经分析发现，住院患者中军人所占比例由2016年的3.03%，上涨到2019年的5.39%，特别是2018年最高为6.69%，表明随着部队医院“停偿服务”的展开，部队官兵医疗需求得到进一步释放。此外，有研究表明[15-16]，军人住院疾病构成中，训练伤位于首位，这就间接导致材料费所占比例升高。

3.2 住院天数、入院次数及有无手术是影响住院费用较为重要的因素

通过住院费用的影响因素分位数回归，得到了所有低、中、高分位数下的回归模型。本研究发现，住院天数和入院次数在各费用段均为住院总费用增长的危险因素。住院天数、入院次数除了与患者病情严重程度有关，也受医务人员医疗水平及医院管理制度影响。严重的疾病不仅会增加手术的难度，也会因术后恢复难度大，增加住院天数、入院次数和住院费用。

进一步分析发现，1次入院的患者占总入院患者的74.78%，而1次入院患者中又有20.33%的患者有骨折或其他不同程度的损伤，这就导致1次入院患者材料费中位费10 386.85元，高于入院2次、3次及以上患者的3 633.62元和952.52元。且1次入院患者材料费占总1次住院费用的36.42%，高于药品费的27.12%；而2次、3次及以上入院患者药品费占其总住院费用的33.25%，高于材料费(18.60%)。

因此，我们有理由推断住院1次患者多是与损伤性疾病有关，需辅以手术、材料等治疗，而2次、3次及以上入院患者多与长期慢性病有关，这就导致了1次入院患者费用高于2次、3次及以上。针对这一问题，需降低1次入院患者的材料费，加强外科科室高值耗材管控，在保障患者健康安全的前提下，鼓励医务工作者优先选用低价优质耗材[17]。

3.3 继续加大医疗保险覆盖率，做好老龄群体的预防保健工作

经研究发现，住院费用也受到付费方式的影响，自费患者的住院费用高于医保患者。进一步分析显示，扬州市基本医疗保险虽已有一个较高的覆盖率(93.50%)[18]，但仍低于江苏省平均水平(97.30%)[19]，也低于同期国家的96.74%[20]。因此，这就需要政府部门既要继续扩大医疗保险覆盖面，倡导全民医保，增强医保意识，减少因重大疾病带来的经济损失。

此外，通过以上分析，注意到住院费用随着年龄的增长而增加，这是由于伴随着年龄的增长，身体各个系统机能开始减退，逐渐出现不同程度的合并症和并发症。据《2019年扬州市国民经济和社会发展统计公报》显示，截至2019年底，扬州市65周岁及以上人口为88.92万人，占总人口的19.55%[18]，高于全国同期平均水平(12.60%)[21]。因此，老年群体也应积极采取预防措施，配合医务人员进行专项疾病复查和定期随访检查，以减少并发症合并症的发生，从而降低住院费用[22]。