环Fq+vFq+v2Fq上的斜准循环码
李建豪,吴化璋
(安徽大学 数学科学学院,安徽 合肥 230601)
循环码是编码理论中的重要组成部分,由于其丰富的代数结构,在纠错码中起着至关重要的作用。关于循环码和准循环码已经有大量文献资料,但很多研究都是关于交换环的。在最近的研究中,主要集中在非交换环上的循环码、准循环码和常循环码。斜多项式环作为非交换环的一个重要类别,也得到了很多学者的关注。
非交换环上循环码的研究最早是由Boucher等[1]讨论的,他们研究了斜多项式环Fq[x,θ]上的循环码,其中Fq是一个有限域且θ是Fq上的一个自同构。准循环码也是一类重要的线性码,包括循环码。因此很多学者开始研究斜准循环码。Abualrub等[2]研究了有限域上的斜准循环码,给出了其生成多项式;Bhaintwal[3]对伽罗瓦环上斜准循环码进行了研究,给出了其自由的一个充分条件; Boucher等[4]给出了有限域上θ-循环码对偶的一些结果;Siap等[5]阐明了有限域上任意长度、任意条件下的斜循环码的结构,因此Fq上斜循环码得到进一步推广;Abualrub等[6]研究了环F2+vF2上的斜循环码,并给出了在该环上的斜循环码的生成多项式,开启了非链环上斜循环码的研究;Mohammad[7]和Gao[8]进一步推广文献[6]的结果,分别研究了环F3+vF3和环Fp+vFp上的斜循环码;Mehmet等[9]研究了环Fq+vFq上的斜准循环码,给出了1-生成元斜准循环码的生成元集。借鉴上述研究,本文考虑非链环Fq+vFq+v2Fq上的斜准循环码,其中v3=v。显然v2=1时,Fq+vFq上斜准循环码可看作是文献[7-8]中斜循环码的推广。同时又探讨了此非链环上斜准循环码与有限域Fq上斜准循环码之间的联系。
1 预备知识
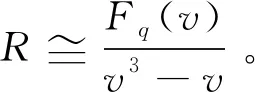
定义环R上的一个自同构
σs:Fq+vFq+v2Fq→Fq+vFq+v2Fq,
x+vy+v2zxps+vyps+v2zps。
根据这个自同构,先给出斜多项式环的定义。

易知R[x,σs]是一个非交换环。
对于任意的f(x),g(x)∈R[x,σs],如果存在一个多项式p(x)∈R[x,σs],使得f(x)=p(x)g(x),则g(x)称为f(x)的右因式。左因式也可以类似定义。
定义2设f(x),g(x)∈R[x,σs],若存在d(x)∈R[x,σs]是f(x)和g(x)的一个右公因式,且f(x)和g(x)的其他右公因式都是d(x)的右因式,则称d(x)为f(x)和g(x)的最大右公因式,记为d(x)=gcrd(f(x),g(x))。
两个多项式的最大左公因式(gcld)也用类似的方法定义。
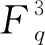
a+vb+v2c(a,a+b+c,a-b+c)。

如果C是R上长为n的线性码,定义:
则C1,C2和C3都是Fq上长为n的线性码。由文献[10]知,R上长为n的线性码C可以唯一分解为
C=(1-v2)C1⊕(v2+v)C2⊕(v2-v)C3。
2 环R上斜准循环码
给出环R上斜准循环码的定义。
定义3设σs是环R的自同构,称C是R上长为N=nl斜准循环码,若C满足以下两个条件:
(1)C是RN的R-子模;
(2) 若
则
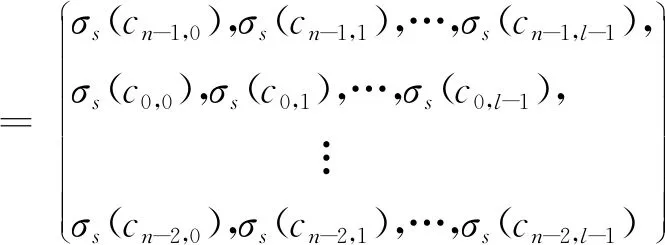
其中τl是斜准循环移位算子。
从定义3可以看出,R上指标为l长为N的斜准循环码在映射τl下是不变的线性码。如果这里l=1,则它就是环R上的斜循环码; 如果自同构σs是单位自同构,则它又是环R上通常的准循环码。

p(x)(q1(x),q2(x),…,ql(x))=
(p(x)q1(x),p(x)q2(x),…,p(x)ql(x))。
定义一个映射
c(c0(x),c1(x),…,cl-1(x))。


证明设C是R上长为N=nl的斜准循环码,c=(c0,0,…,c0,l-1,c1,0,…,c1,l-1,…,cn-1,0,…,cn-1,l-1)∈C。因此,有φ(c)=(c0(x),c1(x),…,cl-1(x))∈φ(C)。则
xφ(x)=(xc0(x),xc1(x),…,xcl-1(x))=

φ(C)。


所以有
φ(τl(c))=x(c0(x),c1(x),…,cl-1(x))=
(xc0(x),xc1(x),…,xcl-1(x))∈D。
故τl(c)∈C,C是环R长为N=nl的斜准循环码。
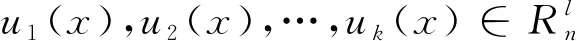
C={f(x)u(x)=(f(x)u1(x),f(x)u2(x),…,
f(x)ul(x))|f(x)∈Rn}。
斜循环码作为斜准循环码的一种特殊情况,也具有丰富的性质。
引理2设C是由u(x)生成的斜循环码,且在R[x,σs]中有xn-1=h(x)u(x)。若p(x)与h(x)互素,则C=〈p(x)u(x)〉。
证明易知,〈p(x)u(x)〉⊆C。下面证明C⊆〈p(x)u(x)〉。因为p(x)与h(x)互素,所以存在a(x),b(x)∈R[x,σs], 使得a(x)p(x)+b(x)h(x)=1。现在等式两边同时乘以u(x),有a(x)p(x)u(x)+b(x)h(x)u(x)=u(x),即a(x)p(x)u(x)=u(x) (modxn-1)。可以得到u(x)∈〈p(x)u(x)〉。故C=〈p(x)u(x)〉。

(c0(x),c1(x),…,cl-1(x))ci(x)。
设φi(C)=Ci。显然,映射φi是一个模同态。所以Ci是Rn的R[x,σs]-子模,即,Ci是R上长为n的斜循环码。如果Ci=〈ui(x)〉,其中ui(x)是xn-1=hi(x)ui(x)的右因式,且pi(x)与ui(x)互素。由引理2知,C的生成元有如下形式
u(x)=(p1(x)u1(x),p2(x)u2(x),…,pl(x)ul(x))。
设C是R上由u(x)=(p1(x)u1(x),p2(x)u2(x),…,pl(x)ul(x))生成,长为N=nl的1-生成元斜准循环码。定义一个首一多项式为
u(x)=gcld(u(x),xn-1)=gcld{p1(x)u1(x),
p2(x)u2(x),…,pl(x)ul(x),xn-1}。
定理1设C是R上由u(x)=(p1(x)u1(x),p2(x)u2(x),…,pl(x)ul(x))生成,长为N=nl的1-生成元斜准循环码,其中ui(x)是xn-1的一个首一的右因式,且
则C是秩为n-deg(u(x))的自由斜准循环码,且一组基为
S={u(x),xu(x),…,xn-deg(u(x))-1u(x)},
其中u(x)=gcld(u(x),xn-1)。
证明首先证明集合S能生成码C。因为u(x)=gcld(u(x),xn-1),故存在一个首一多项式v(x),使得xn-1=u(x)v(x)。设deg(u(x)) =k,则deg(v(x))=n-k。码C中元素为c(x)=a(x)u(x),其中a(x)∈Rn。由右除法知,存在两个多项式q(x),r(x)∈R[x,σs],使得
a(x)=q(x)v(x)+r(x),0≤deg(r(x)) 又因为u(x)=gcld(u(x),xn-1),故存在一个多项式s(x)∈Rn,使得u(x)=u(x)s(x)。又xn-1是R[x,σs]的中心,所以有xn-1=u(x)v(x)=v(x)u(x)。则 v(x)u(x)=v(x)u(x)s(x)=u(x)v(x)s(x)= (xn-1)s(x)≡0 (mod(xn-1))。 进一步可以得到 c(x)=a(x)u(x)=(q(x)v(x)+r(x))u(x)= 因为deg(r(x)) 下面证明S是线性无关的。设多项式a(x)= ui(x)=0,xn-1是a(x)pi(x)ui(x)的因式。又因为xn-1是a(x)(xn-1)的因式,故 xn-1|gcld(a(x)p1(x)u1(x),…,a(x)pl(x)ul(x), a(x)(xn-1)),即xn-1|a(x)u(x)。因为deg(a(x)u(x))=n-1 设a=(a0,a1,…,an-1)∈Rnl,b=(b0,b1, …,bn-1)∈Rnl,其中ai=(ai,0,ai,1,…,ai,l-1)∈Rl,bi=(bi,0,bi,1,…,bi,l-1)∈Rl,i=0,1,…,n-1。 定义a和b的欧几里得内积为 则C关于欧几里得内积的对偶码定义为 C⊥={b∈Rnl|a·b=0,∀a∈C}, 斜准循环码的对偶码也是斜准循环码。 定理2设C是R上长为N=nl的线性码。则C是关于自同构σs的斜准循环码当且仅当C⊥是关于自同构σs,长为N=nl的斜准循环码。 其中下标i+n-1是对n取模。所以τl(b)∈C,即C⊥是长为N=nl斜准循环码。 例1设R=F4+vF4+v2F4,当n=5时,有 x5-1=(x+3)(x4+x3+x2+x+1)。 若C是环R上由u(x)=(u1(x),u2(x))生成,长为10的1-生成元斜准循环码,其中u1(x) =u2(x)=x4+x3+x2+x+1。由定理1知,gcld(u(x),x5-1)=x4+x3+x2+x+1且C的一组基为{u(x)},因此|C|=64,Lee重量为10。可以得到码C在Gray映射φ下的象是F4上参数为(30,43,10)的线性码。 本文所用的方法与文献[11]中的方法类似,不同之处在于本文研究的是斜准循环码。 定理3设C=(1-v2)C1⊕(v2+v)C2⊕(v2-v)C3是环R上长为N=nl的线性码,则C是R上关于自同构σs的斜准循环码当且仅当C1,C2,C3分别是Fq上关于自同构σs,长为N的斜准循环码。 证明先证明必要性。对于任意的r=(r0,0, …,r0,l-1,r1,0…,r1,l-1,…,rn-1,0,…,rn-1,l-1)∈C,记ri,j=(1-v2)ai,j+(v2+v)bi,j+(v2-v)ci,j,其中ai,j,bi,j,ci,j∈Fq,0≤i≤n-1,0≤j≤l-1。设 a=(a0,0,…,a0,l-1,a1,0,…,a1,l-1,…,an-1,0,…,an-1,l-1), b=(b0,0,…,b0,l-1,b1,0,…,b1,l-1,…,bn-1,0,…,bn-1,l-1), c=(c0,0,…,c0,l-1,c1,0,…,c1,l-1,…,cn-1,0,…,cn-1,l-1), 有a∈C1,b∈C2,c∈C3。假设C1,C2,C3是Fq上关于自同构σs,长为nl的斜准循环码,则 τl(a)= 同理, τl(b)= τl(c)= 所以τl(r)= (1-v2)τl(a)+(v2+v)τl(b)+(v2-v)τl(c)∈C。故C是R上关于自同构σs,长为nl的斜准循环码。 下面证明充分性。因为C是环R上关于自同构σs,长为nl的斜准循环码,所以τl(r)∈C。又因(1-v2)τl(a)+(v2+v)τl(b)+(v2-v)τl(c) =τl(r),故(1-v2)τl(a)+(v2+v)τl(b)+(v2-v)τl(c)∈C。因此τl(a)∈C1,τl(b)∈C2,τl(c) ∈C3,C1,C2,C3是Fq上关于自同构σs,长为nl的斜准循环码。 定理4设C=(1-v2)C1⊕(v2+v)C2⊕(v2-v)C3是环R上长为N=nl的斜准循环码,则 C=〈(1-v2)g1(x),(v2+v)g2(x),(v2-v)g3(x)〉, 其中g1(x)=(g11(x),g12(x),…,g1l(x)),g2(x)= (g21(x),g22(x),…,g2l(x)),g3(x)=(g31(x),g32(x),…,g3l(x))分别是C1,C2,C3的生成多项式。 证明由定理3可得,C1,C2,C3是Fq上长为N的斜准循环码,从而有C1=〈g1(x)〉,C2= 〈g2(x)〉,C3=〈g3(x)〉,且C=(1-v2)C1⊕(v2+v)C2⊕(v2-v)C3,于是有C={c(x)|c(x)=(1 -v2)f1(x)+(v2+v)f2(x)+(v2-v)f3(x),f1(x)∈C1,f2(x)∈C2,f3(x)∈C3}。因此 C⊆〈(1-v2)g1(x),(v2+v)g2(x), (v2-v)g3(x)〉。 反之,对任意的f(x)=(1-v2)k1(x)g1(x)+ (v2+v)k2(x)g2(x)+(v2-v)k3(x)g3(x)∈〈(1-v2)g1(x),(v2+v)g2(x),(v2-v)g3(x)〉,其中k1(x),k2(x),k3(x)∈R[x,σs]/〈xn-1〉。这里显然有 ki(x)=(1-v2)ai(x)+(v2+v)bi(x)+ (v2-v)ci(x), 其中ai,bi,ci∈Fq[x,σs],i=1,2,3, 因此 (1-v2)ki(x)=(1-v2)ai(x), (v2+v)ki(x)=(v2+v)bi(x), (v2-v)ki(x)=(v2-v)ci(x)。 由于C1,C2,C3是Fq上长为N的斜准循环码,故ai(x)gi(x)∈Ci,i=1,2,3,从而〈(1-v2)g1(x), (v2+v)g2(x),(v2-v)g3(x)〉⊆C。 综上,C= 〈(1-v2)g1(x),(v2+v)g2(x),(v2-v)g3(x)〉。 定理5设C1,C2,C3是Fq上分别由多项式g1(x)=(g11(x),g12(x),…,g1l(x)),g2(x)=(g21(x),g22(x),…,g2l(x)),g3(x)=(g31(x),g32(x),…,g3l(x))生成的斜准循环码。若C=(1-v2)C1⊕ (v2+v)C2⊕(v2-v)C3是R上长为N=nl的斜准循环码,则存在g(x)=(g1(x),g2(x),…,gl(x)),其中gi(x)∈R[x,σs],i=1,2,…,l,使得C=〈g(x)〉,其中g(x)=(1-v2)g1(x)+(v2+v)g2(x)+(v2-v)g3(x)。 证明由定理4,可假设C=〈(1-v2)g1(x), (v2+v)g2(x),(v2-v)g3(x)〉,其中g1(x),g2(x),g3(x)分别是C1,C2,C3的首一多项式。令g(x)=(1-v2)g1(x)+(v2+v)g2(x)+(v2-v)g3(x)。显然,〈g(x)〉⊆C。注意到有 因此C⊆〈g(x)〉。故C=〈g(x)〉。 又因为gij(x)是xn-1的首一右因式,i=1,…,n;j=1,…,l。 则存在 r1(x),r2(x),r3(x) ∈Fq[x,σs]/〈xn-1〉, 使得 xn-1=r1(x)g1(x)=r2(x)g2(x)= r3(x)g3(x), 从而 xn-1=[(1-v2)r1(x)+(v2+v)r2(x)+ (v2-v)r3(x)]g(x), 因此g(x)|xn-1。g(x)的唯一性可由g1(x),g2(x),g3(x)的唯一性得到。 本文给出了R=Fq+vFq+v2Fq上斜准循环码的生成元集,且在定理3中确定了其与Fq上斜准循环码的联系。同时,证明了R上斜准循环码的对偶还是斜准循环码。在后续工作中,还可以考虑研究其他非交换环上的斜准循环码。

3 R上斜准循环码的直和分解
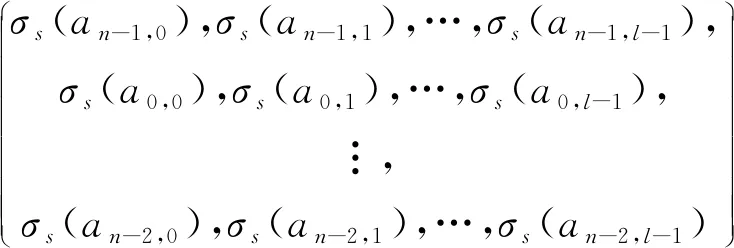
4 结束语

