顾及信噪比的蝙蝠选星算法
王晖,苏晓庆,曲国庆,刘春科
(山东理工大学 建筑工程学院,山东 淄博 255049 )
一般来说,测站的观测时间越长、卫星数目越多,定位精度就越高;然而卫星信号功率低,容易受到干扰和欺骗、多路径效应、卫星信号遮挡等因素的影响,导致卫星失锁,实际定位结果偏离真实值[1-4]。对于上述问题,可采用选星方法,剔除受影响较大的卫星。
常用的选星方法有最小几何精度因子(geometric dilution of precision,GDOP)遍历法和最大体积法。最小GDOP遍历法计算过程中存在矩阵相乘和求逆,当卫星数目较多时,该方法运算耗时长,影响定位的时效性。最大体积法将卫星围成的几何体积作为选星结果的评价标准,能有效降低选星所消耗的时间,但其精度低于遍历法。为了克服上述两种方法的缺陷,出现了许多创新性方法,例如行列式、三维凸包和遗传等选星算法[5-7],均在保证精度损失最小的前提下,提高选星效率,但在选星过程中未考虑其他影响定位精度的干扰因素。
蝙蝠算法(bat algorithm,BA)已被应用于多阈值图像分割[8]、无线网络流量预测[9]和机器人路径规划[10]等领域,但是BA算法用于选星方面的研究还未得见,因此,结合定位精度和选星时效性问题,将信噪比(signal-to-noise ratio,SNR)和BA算法引用到选星中,剔除空间分布差和受干扰大的卫星,探讨选星算法在定位受干扰、结果偏差较大情况下的有效性,改善定位精度及提高选星效率。
1 几何精度因子
在卫星定位中,定位精度可以用GDOP和观测精度的乘积来表示,当观测精度一定时,几何精度因子越小,定位精度越高[11]。
σA=σ×GDOP,
(1)
(2)

(3)
式中:σA为定位精度;σ为观测精度;H为观测矩阵;HC为北斗卫星导航系统(Beidou navigation satellite system,BDS)观测矩阵;HG为全球定位系统(global positioning system,GPS)观测矩阵;HR为格洛纳斯卫星导航系统(global orbiting navigation satellite system,GLONASS)观测矩阵;HE为伽利略卫星导航系统(Galileo satellite navigation system,GALILEO)观测矩阵。
2 顾及信噪比的蝙蝠选星算法
2.1 算法的基本思想
SNR是指载波信号强度与噪声强度的比值,可衡量卫星测距信号的质量,并间接反映了卫星载波相位的测距精度[12]。通常,卫星受干扰越大,信噪比越低,观测数据质量越差,因此将信噪比作为选星的一个重要参考指标。
BA算法是一种群体智能搜索优化算法,具有参数少、实现简单、空间搜索能力强、搜索速度快等优点,因而能够提高选星效率和局部搜索能力,在准确性和有效性方面优于其他算法[13]。蝙蝠搜索目标时会发出脉冲声音,通过接收周围物体反弹回来的声音,来感知与周围物体之间的距离,同时还会以一种特殊的方式辨别目标与障碍物。
将SNR与BA算法融合引入到选星中,称为顾及信噪比的蝙蝠选星算法。算法的基本思想:设置信噪比阈值,剔除低于阈值的卫星,将GDOP作为适应度函数,利用上述BA算法的优点,得到最小适应度值对应的卫星组合,即为所选卫星。
2.2 算法的具体步骤
在算法中,设某时刻的可视卫星数为m颗,选择其中的n颗卫星,使其组合的GDOP值最小,作为选星目标。将每种卫星组合视为一个蝙蝠,其位置为卫星组合的坐标。蝙蝠可以根据与目标之间的距离自动调整飞行速度、脉冲响度和脉冲频率。当蝙蝠离目标越远时,飞行速度越快,脉冲响度越大,脉冲频率越小;反之,飞行速度越慢,脉冲响度越小,脉冲频率越大。通过不断更新蝙蝠的位置,最后得出选星结果。顾及信噪比的蝙蝠选星算法具体步骤为:
步骤1 计算所有可视卫星信噪比的平均值,并以其为阈值,将信噪比小于阈值的卫星剔除,为初始种群提供先验条件。
(4)
步骤3 参数初始化,设置蝙蝠种群数量M、迭代次数N、初始速度vi、声波频率i、脉冲响度Ai和脉冲频率ri;设置速度范围[-1,1],频率范围[0,1];设置脉冲频率增加系数γ为0.95,脉冲响度衰减系数α为0.95[13-16]。
步骤4 计算并评价每个蝙蝠位置对应的适应度值,找出最小适应度值所对应的卫星组合。
步骤5 判断当前适应度值、脉冲频率、脉冲响度和迭代次数是否满足终止条件,若满足,算法结束,输出卫星组合;若不满足,继续进行步骤6。

fi=fmin+(fmax-fmin)β,
(5)
(6)
(7)
步骤7 生成[0,1]上的随机数rand1,如果rand1>ri,在最优卫星组合周围根据公式(8)再生成一个新的卫星组合,否则随机飞行产生新的卫星组合。
xnew=xold+εAt,
(8)
式中:ε∈[-1,1]是一个随机数;At为所有蝙蝠在同一时间段的平均响度。
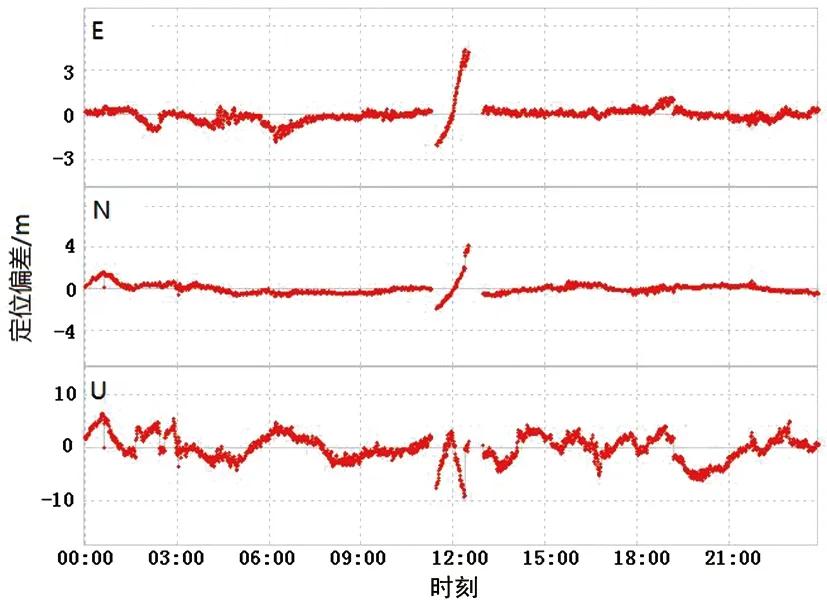
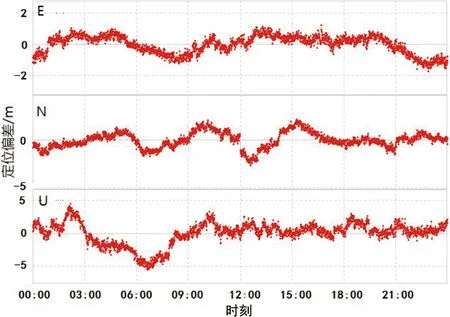
步骤8 生成[0,1]上的随机数rand2,如果rand2 (9) 3.1.1 数据来源 利用MGEX平台提供的ABMF、BJNM、BJFS基准站多系统观测数据进行分析,观测时长为24 h,采样间隔为30 s。ABMF基准站包含GPS、GLONASS和Galileo导航系统观测数据和SBAS星基增强系统观测数据;BJNM基准站包含GPS、GLONASS和Galileo导航系统观测数据;BJFS基准站包含GPS和GLONASS导航系统观测数据。 3.1.2 定位分析 RTKLIB是日本东京海洋大学开发的一款用于全球导航卫星系统(global navigation satellite system,GNSS)定位的开源程序包,采用RTKLIB中的RTKPOST模块对数据进行单点定位解算,解算结果如图1、图2和图3所示。将国际GNSS服务(international GNSS service,IGS)组织在数据服务中心提供的站点坐标作为精度评定的参考值,统计出ABMF基准站(00:15:00、11:20:00)、BJNM基准站(00:05:00、04:25:00)和BJFS基准站(06:37:30、06:56:00)六个定位偏差较大的时刻,其中ABMF基准站11:20:00时刻,E和U方向的偏差均超过5 m,定位精度低。 图1 ABMF基准站各时刻单点定位结果 图2 BJNM基准站各时刻单点定位结果 图3 BJFS基准站各时刻单点定位结果 3.1.3 信噪比统计 利用数据检核软件TEQC,对基准站各时刻进行检核,获得各时刻的L1、L2载波信噪比(分别用SN1、SN2表示),见表1。 表1 基准站各时刻信噪比检核结果 根据信噪比评价标准可以得知,信噪比大于36 dB,信号受干扰少,强度等级高[17]。由表1可知,三个基准站的L1载波信噪比大于36 dB,信号强度高;而BJNM基准站和BJFS基准站06:56:00时刻的L2载波信噪比低于36 dB,信号强度低,受干扰大。 为保证有足够的卫星参与定位解算,同时还要避免观测数据的浪费,限定选星数目不小于多系统定位要求的5颗卫星,且不大于已有卫星总数的60%;因此,设定选星数目为10~11颗,可以兼顾精度和效率,且GDOP损失较小[18-19]。以BJNM基准站00:05:00时刻为例,在20颗卫星中,拟选取11颗;同时,设计了四种实验方案,通过不同方案的对比分析,来验证顾及信噪比的蝙蝠选星算法的有效性。方案一,保留全部卫星;方案二,采用最小GDOP遍历法选取卫星;方案三,采用BA选星算法选取卫星;方案四,采用顾及信噪比的蝙蝠选星算法选取卫星。 BJNM基准站不同选星方案的耗时(文中耗时是指在Intel(R) Core(TM)2 Quad CPU Q6600 @ 2.40 GHz 2.39 GHz处理器下,matlab2014b程序运行时间)见表2。 表2 BJNM基准站00:05:00时刻不同方法选星耗时 由表2可知,方案四选星耗时最少、效率最高,方案三次之,方案二耗时最长、效率低。 由表3、表4和表5可知,在BJNM基准站的04:25:00时刻,方案三选星定位结果偏离参考值大于10 m,定位精度较差,与算法容易收敛过早,陷入局部极值的特点有关。与其他方案相比,方案四能较好地改善定位精度,剔除信号受干扰信噪比低的卫星,不易受局部极值的影响,并且可选取几何构型较优的卫星组合进行定位解算。 表3 ABMF基准站各时刻选星定位精度 表4 BJNM基准站各时刻选星定位精度 表5 BJFS基准站各时刻选星定位精度 结合表1、表3、表4和表5,以BJNM基准站为例,在L2载波信噪比小于36 dB,受干扰大的情况下,方案四的定位精度高,说明该方法在卫星信号受干扰时,也能改善定位精度。 综合四种方案的选星耗时和定位结果,方案四能提高选星效率,改善定位精度,减少计算负担,可用于实时导航定位。 根据卫星信噪比和空间分布对定位精度的影响,用顾及信噪比的蝙蝠选星算法进行选星分析。在选星耗时方面,该方法有效降低选星所用时间,保证选星定位的实时性。从定位结果上看,该方法可以对信号受干扰、定位偏差大的时刻进行改正,改善了定位精度。与最小GDOP遍历法相比,顾及信噪比的蝙蝠选星算法提高了选星效率,且整体的定位精度优于最小GDOP遍历法。要进一步提高定位精度,在后续研究工作应考虑除信噪比外的其他影响因素。 致谢 感谢东京海洋大学共享的RTKLIB开源程序包,UNAV-CO Facility共享的TEQC公开免费软件。
3 实验分析
3.1 数据来源与分析


3.2 选星分析





4 结束语

