带式舟桥泛水展开过程中扭力杆受力计算模型

丁 勇， 林铸明， 李 欢， 蔡正宇

(陆军研究院，江苏 无锡 214035)

带式舟桥是一种集桥脚、承重结构和通载桥面于一体的浮桥结构，具有结构整体性好、架设时间短、吃水浅等优点[1]。国外军事发达国家都大力发展带式舟桥装备，较为先进的带式舟桥装备有俄罗斯ΠΠ-2015舟桥纵列、德国FFB-2000带式舟桥、美国IRB改进型带式舟桥和法国PFM F1型摩托化浮桥等[2-3]。为了充分利用装载空间，带式舟桥通常采用折叠式的结构型式，泛水后通过人工将两个方舟的上部扣环以及方舟与尖舟的底部铰链连接成整体进行承载。泛水后自动展开是带式舟桥的优点。

在带式舟桥的研制和使用过程中，国外学者对其进行了大量的研究[4-6]。国内研究方面，周新年等[7]提出了一种基于玻璃钢/钢材复合结构的结构方案；佐晓波[8]对铝合金材料的带式舟桥舟体进行系统研究，采用数值模拟方法计算得出了舟体的承载能力；Zhang等[9]对不同水深条件下浮桥在移动荷载作用下的分析模型进行了研究，得出了水深对浮桥动力响应影响不大的结论；付世晓等[10-12]对通载浮桥的非线性水弹性响应进行了系统研究，得出了通载速度对带式舟桥动力响应影响较大的结论；孙文俊等[13]对舟桥器材与水流的相互作用进行了研究，并对其进行了试验验证；王月安等[14-15]则重点对带式舟桥的接头疲劳性能进行了较为系统的研究，为带式舟桥装备研制提供了很好的技术支撑。

目前对带式舟桥的研究主要集中在结构材料、动力响应、水力性能和连接接头等方面，对泛水过程的扭力杆受力分析研究不充分。扭力杆提供足够大的扭矩是确保舟桥泛水展开顺利的必要条件。在现役带式舟桥研制过程中，扭力杆所需提供扭矩大小是通过试验确定的，缺乏理论计算方法。因此，有必要建立泛水展开过程扭力杆受力计算理论模型，为扭力杆的设计计算提供依据。

本文根据力的平衡原理，采取隔离扭力杆和分阶段求解的方法，通过推导尖舟结构在不同阶段不同受力状态下的受力计算公式，建立扭力杆在带式舟桥泛水展开全过程的受力计算模型，以解决带式舟桥在泛水展开过程中因结构不稳定导致的扭力杆复杂受力问题。

1 泛水展开过程分析

1.1 卸载泛水作业

根据岸坡的不同，带式舟桥卸载泛水的方法可分为强制卸载、自动下滑卸载、倒车急刹车卸载和陡岸卸载4种。

(1)强制卸载。通常在岸坡小于10%时采用，用绞盘钢索拉舟泛水。首先，驾驶员将舟车倒至泛水点，放钢索，2名作业手打开折叠固定钩，取下钢索套圈并将钢索绕过平台尾部导轮下方，拉向舟体前部，通过舟体装卸圆钮上方，再用卸扣与2根钢索的套圈相连。然后，将舟车倒至后轮吃水1/2～2/3轮胎高度，作业手松开紧定具、打开限位销，驾驶员收钢索使舟下滑并泛入水中。

(2)自动下滑卸载。当岸坡大于10%时通常采用自动下滑卸载。第一步，驾驶员将舟车倒至泛水点并放松绑舟钢索，作业手打开折叠固定钩并摘下钢索，驾驶员再收钢索使钢索套圈位于摆动滑轮下方。第二步，将车倒至后轮吃水1/2～2/3轮胎高度，作业手松开紧定具、打开限位销，舟体即靠自重分力自动下滑并泛入水中。

(3)倒车急刹车卸载。当岸坡在10%左右时常采用这种方法。首先，驾驶员将舟车停在离泛水停车位置约5～8 m处，完成自动下滑卸载步骤的第一步，然后作业手松开紧定具，其中1名作业手将并舟具插入限位销的拉手内，指挥驾驶员倒车。当车倒至泛水位置时，在作业手用并舟具打开限位销的同时，驾驶员踩下制动踏板，舟车急停，舟体靠惯性下滑泛水。未能下滑时，可使舟车突然起步将舟体泛入水中。

(4)陡岸卸载。当岸高在2 m以上，在上述方法都不能完成泛水作业时，可使用陡岸卸载法。第一步，舟车开至泛水点停稳，只留限位销防止舟体滑动，其余紧固装置全部摘下，打开折叠固定钩。第二步，使吊车靠近舟车并停稳，吊车配备4根6 m长的钢索、4根3 m长的钢索、4个滑轮和卸扣，按照起吊的方式将钢索套好。第三步，用吊车起吊舟体，待舟体离开舟车后，回转吊臂，将舟体泛入水中，舟体便可在大于0.7 m的水深处自行展开。

1.2 阶段划分及受力分析

从以上作业过程可以看出，无论哪种卸载泛水方式，舟体泛水后都可以大致划分为3个阶段。需要说明的是，这3个阶段并不是完全独立的，在实际过程中是连续的，并且过程十分复杂。

阶段一：河中舟泛入水中到河中舟完全浸入水中但还未展开前。在此阶段，河中舟无论是依靠绞盘钢索(强制卸载)还是依靠重力(自动下滑卸载)滑入水中，都有一定的冲击力，因此当河中舟完全浸入水中时，由排水体积产生的浮力是大于河中舟的重力的，其值可以取为重力与冲击系数的乘积。

阶段二：从河中舟在水中自动展开到展开后呈自由展开状态。在此阶段，由排水体积产生的浮力可以认为与河中舟的重力相等。由于河中舟重力线过方舟铰点不会产生力矩，而浮心与铰点之间有一定距离，因此浮力对方舟铰点而言将产生一个让方舟翻转的力矩。在此过程中，浮力同样会对河中尖舟产生一个力矩。该力矩会使尖舟转向河中方舟上部，是尖舟在翻转过程中需要克服的一个力矩。尖舟重力相对尖舟铰点产生的力矩对尖舟翻转的影响较为复杂，会随着方舟的翻转而改变。

阶段三：从河中舟完全自由展开后到方舟结合前。此阶段可能出现两种状态，一种是尖舟和方舟均顺利展开，全形舟呈完全自由展开状态；另一种是尖舟未顺利展开，置于方舟上部，需要借助吊臂吊开。

2 模型建立

为了准确确定河中尖舟在展开过程中所需扭矩大小，下面对上述3个阶段河中尖舟所受外力和外力矩进行分析。

图1为全形舟折叠后的装车示意图。为了便于分析，在不改变各组成部分重量大小及重心位置的前提下，将其简化为图2。

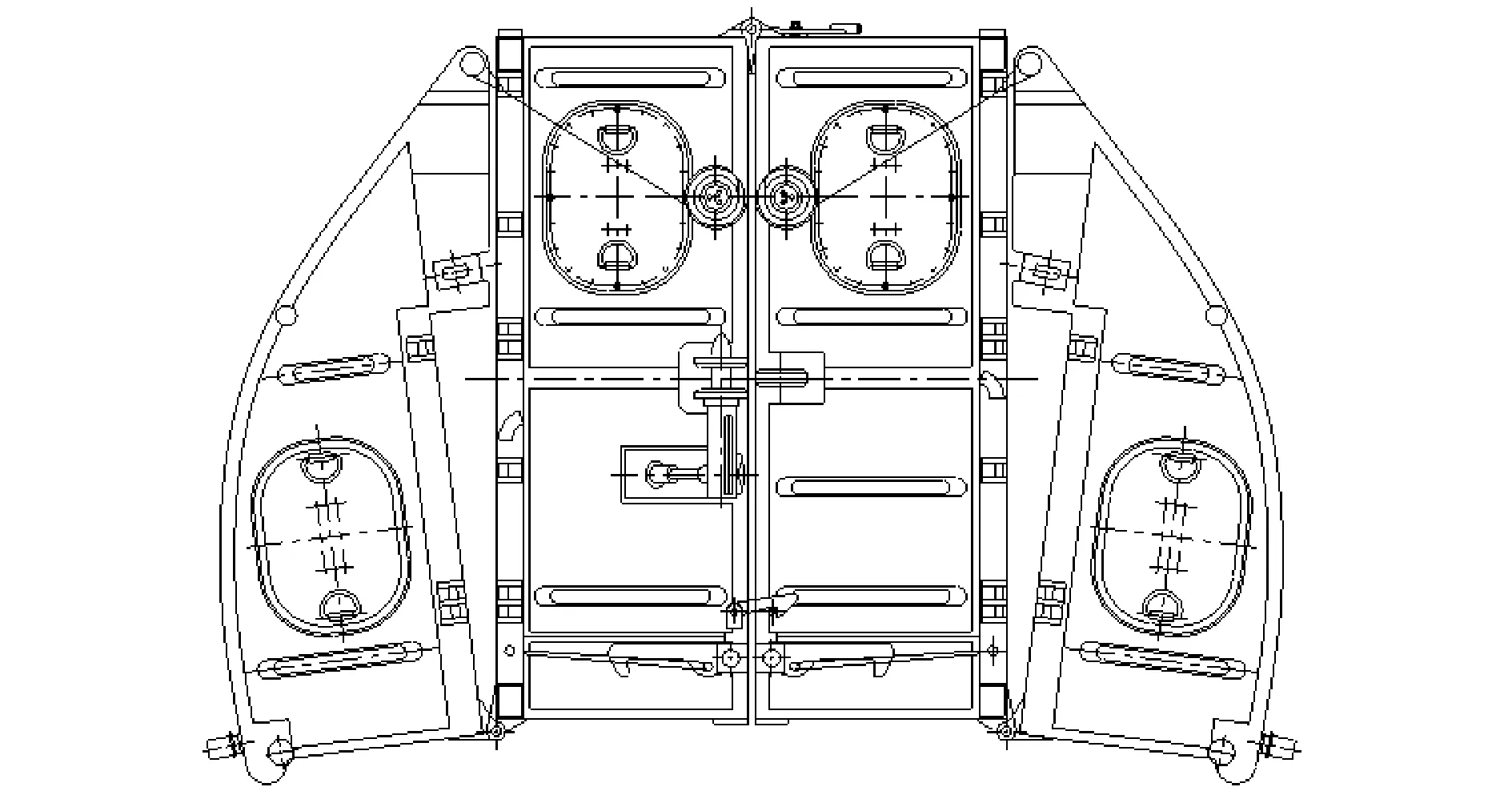
图1 全形舟装车图

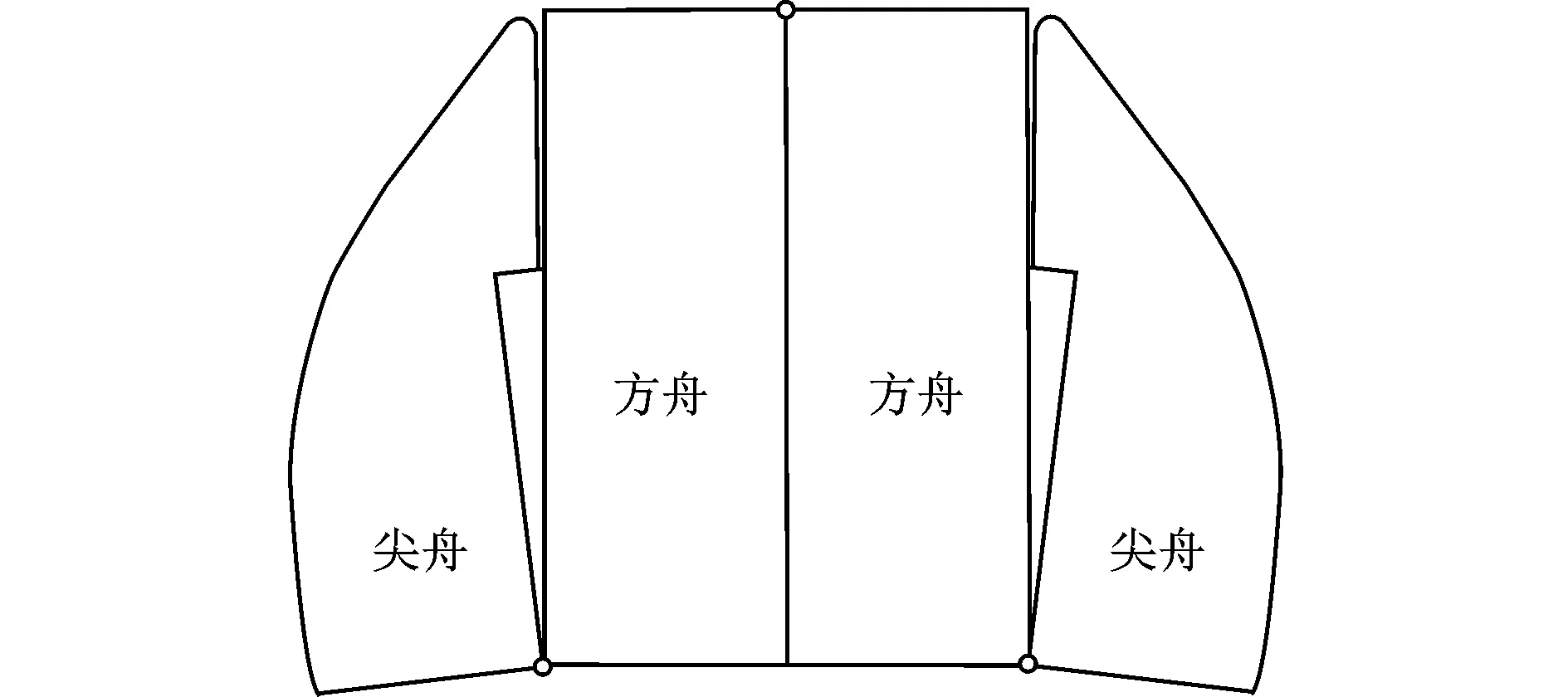
图2 全形舟外形简化示意图

2.1 阶段一

图3为全形舟在阶段一完全浸入水中后尖舟的受力简图。

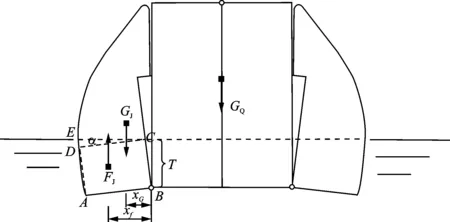
图3 阶段一时尖舟受力简图

图中，GQ为全形舟重量，GJ为尖舟重量，FJ为尖舟所受浮力，T为全形舟吃水深度，xG和xf分别为尖舟重心和浮心距离尖舟铰点的水平距离。在此状态下，根据上述分析，通过力的平衡条件可得

FQ=μGQ

(1)

式中：FQ为全形舟受到的浮力；μ为冲击系数，根据GJB435—88《军用桥梁设计荷载》中关于车辆冲击力的规定，冲击系数最大为1.25，考虑河中舟从运载车上泛入水中的冲击力相对车辆冲击力而言更大，适当地增大该值，取为1.35。其中，FQ可以根据全形舟吃水深度，根据图3所示关系，按式(2)进行计算得出。

FQ=2ρgL(SJ+SF)

(2)

(3)

SF=hF·T

(4)

式中：ρ为水的密度；g为重力加速度，取为10.0 m/s2；L为全形舟长度；SJ为尖舟浸水断面面积；SF为方舟浸水断面面积；hJ为尖舟高度；hF为方舟高度；α为尖舟与方舟之间的夹角。

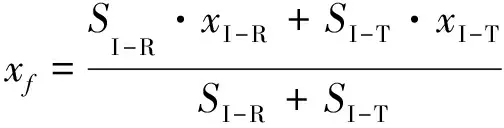
(5)

式中：SI-R为图3中□ABCD面积，SI-T为图3中△CDE面积，xI-R为图3中□ABCD形心至尖舟铰点水平距离，xI-T为图3中△CDE形心至尖舟铰点水平距离，分别为

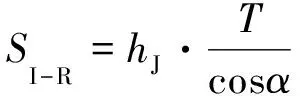
(6)

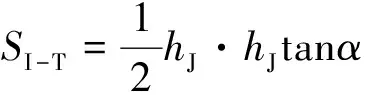
(7)

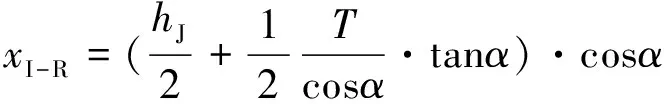
(8)

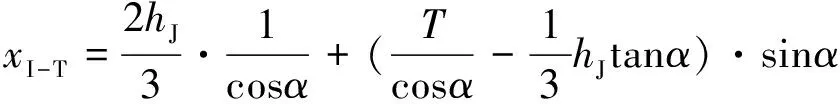
(9)

尖舟受到的浮力为

FJI=ρgLSJ

(10)

此状态下，尖舟受到的相对于铰点的外力矩(不包含扭力杆提供的力矩)为

MWI=FJI·xf-GJ·xG

(11)

需要说明的是，在折叠状态下，尖舟顶部虽然与方舟有接触，但接触点只能承受压力，对尖舟的翻转没有帮助，只能被动抵消浮力与重力之间的力矩差。换言之，如果没有扭力杆提供额外的扭矩，尖舟只能侧置于方舟之上。因此，在后续分析过程中，只需重点分析尖舟浮力与重力对铰点产生的力矩关系。

2.2 阶段二

图4为阶段二中在没有扭力杆作用下全形舟的展开过程示意图。没有扭力杆的作用，尖舟在展开过程中只会侧置于方舟上部而无法展开。因此，可以通过分析这一过程中尖舟所受的外力矩大小确定扭力杆需要提供的扭矩大小。

在方舟自动翻转展开过程中，可以根据几个特殊的翻转角度将阶段二细化为几个状态。一是尖舟下部角点翻转至即将脱离水面时(图5)的翻转角度β1，二是尖舟铰点翻转至即将脱离水面时(图6)的翻转角度β2，三是自由稳定状态时(图7)的翻转角度β3。

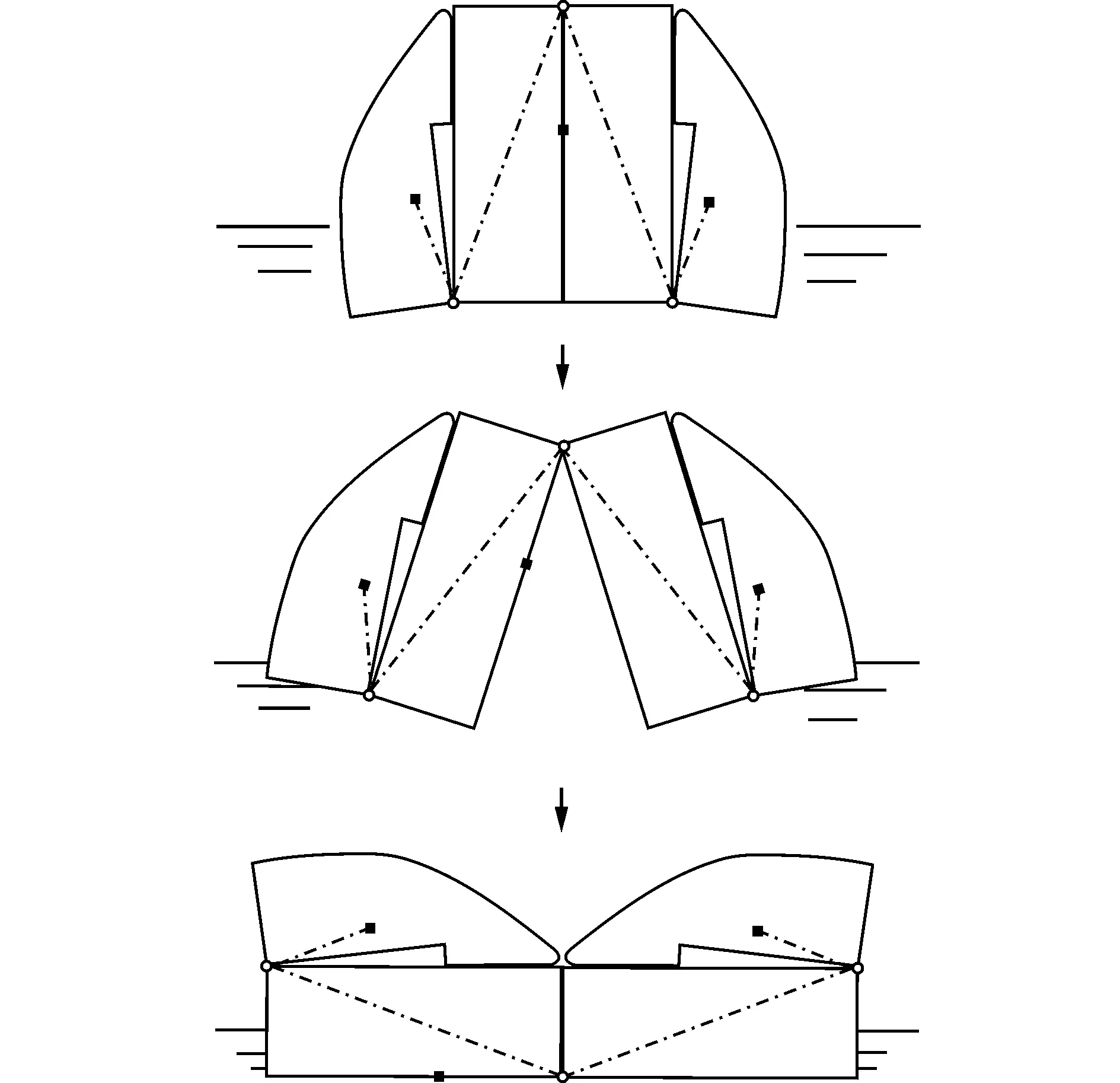
图4 阶段二中在没有扭力杆作用下的展开过程示意图

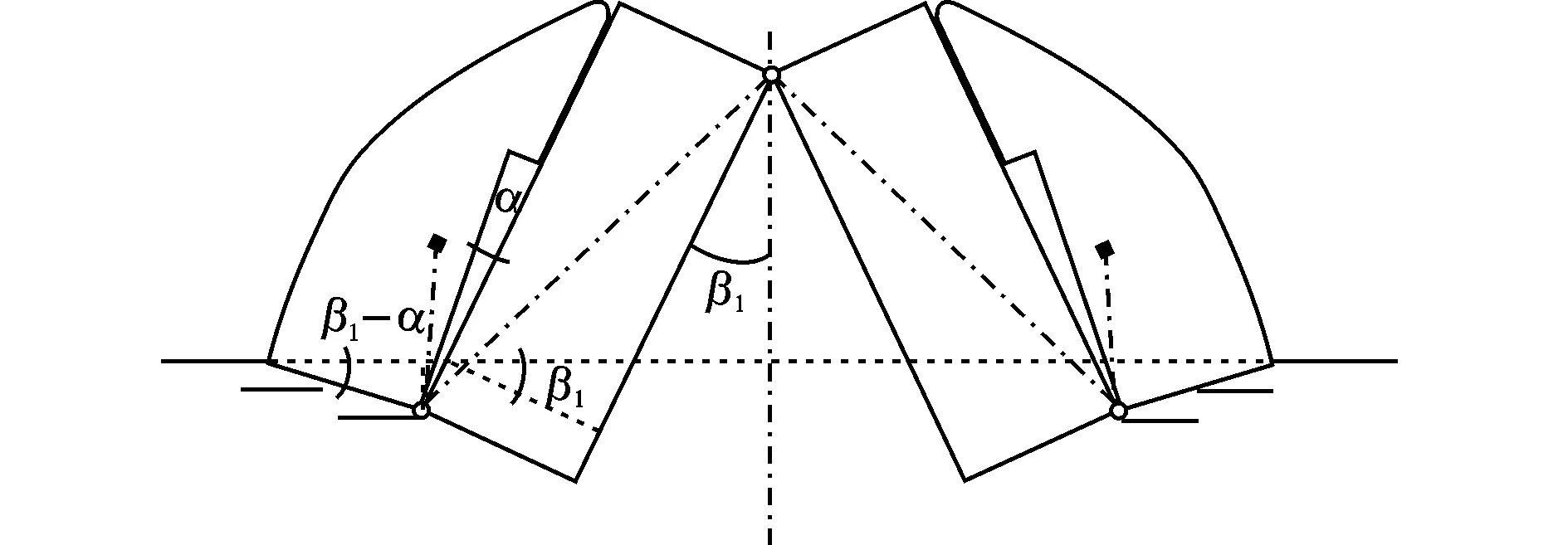
图5 尖舟下部角点翻转至即将脱离水面时状态

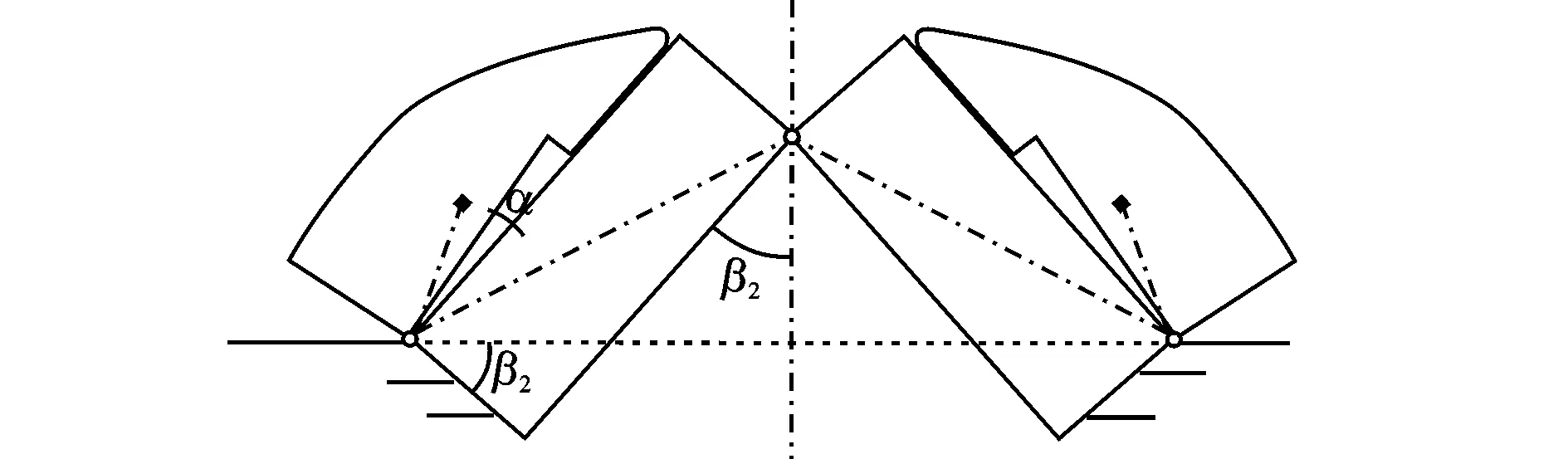
图6 尖舟铰点翻转至即将脱离水面时状态

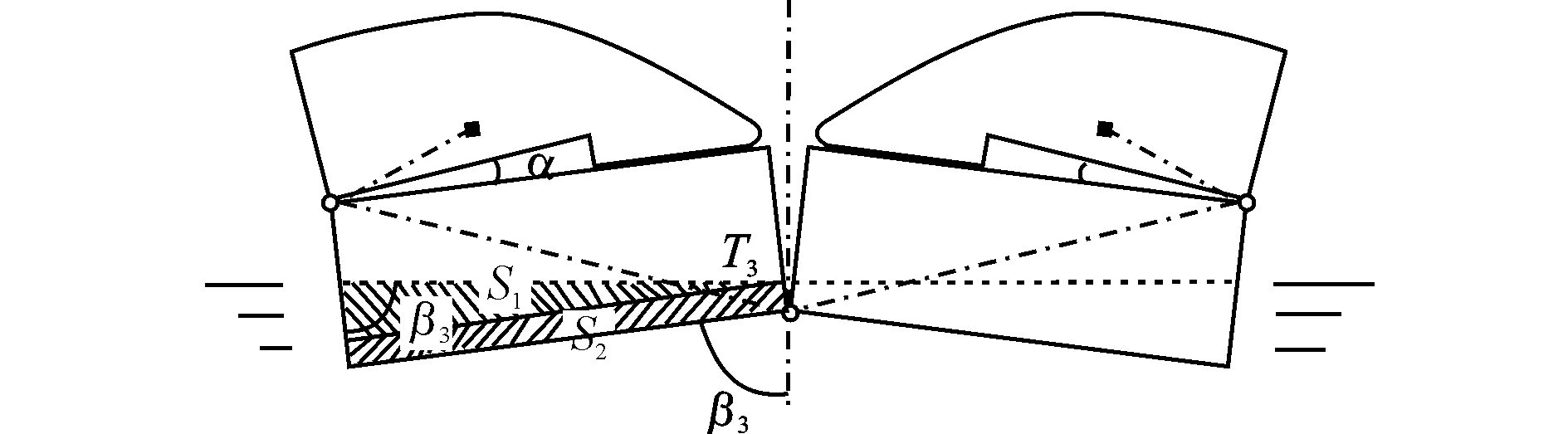
图7 自由稳定状态下力的平衡简图

图5所示为尖舟下部角点翻转至即将脱离水面时的状态。在此状态下，根据力的平衡条件，有

(12)

根据式(12)，即可求得β1。

图6所示为尖舟铰点翻转至即将脱离水面时的状态。在此状态下，根据力的平衡条件，有

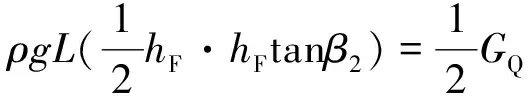
(13)

根据式(13)，即可求得β2。

图7所示为全形舟自由稳定状态。在此状态下，根据力的平衡条件，有

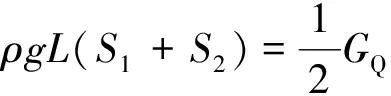
(14)

式中：S1、S2为图中阴影部分面积。分别为

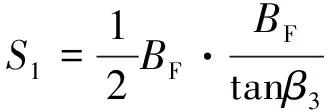
(15)

(16)

式中：T3为此状态下方舟铰点至水面垂直距离，为未知数；β3为翻转角度，同样为未知数；BF为河中方舟宽度。

因此，若要求解β3，还需一个方程。又因为此状态属于自由稳定状态，因此其力矩也处于平衡状态，即浮力线与重力线重合，于是有

(17)

式中：GF为河中方舟重量，xF为方舟重心距全形舟中心线的水平距离，GJ为河中尖舟重量，xJ为尖舟重心距全形舟中心线的水平距离，x1为三角形形心距全形舟中心线的水平距离，x2为矩形形心距全形舟中心线的水平距离。

xF、xJ的几何关系如图8所示，其计算分别为

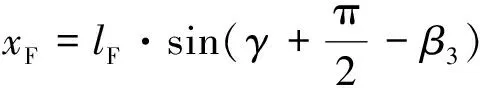
(18)

xJ=2xF-lJ·sin(β3-δ)

(19)

式中：lF为河中方舟重心与方舟铰点之间的距离，lJ为河中尖舟重心与尖舟铰点之间的距离，γ为方舟重心铰点连线与方舟侧面之间夹角，δ为尖舟重心铰点连线与方舟甲板面之间夹角。

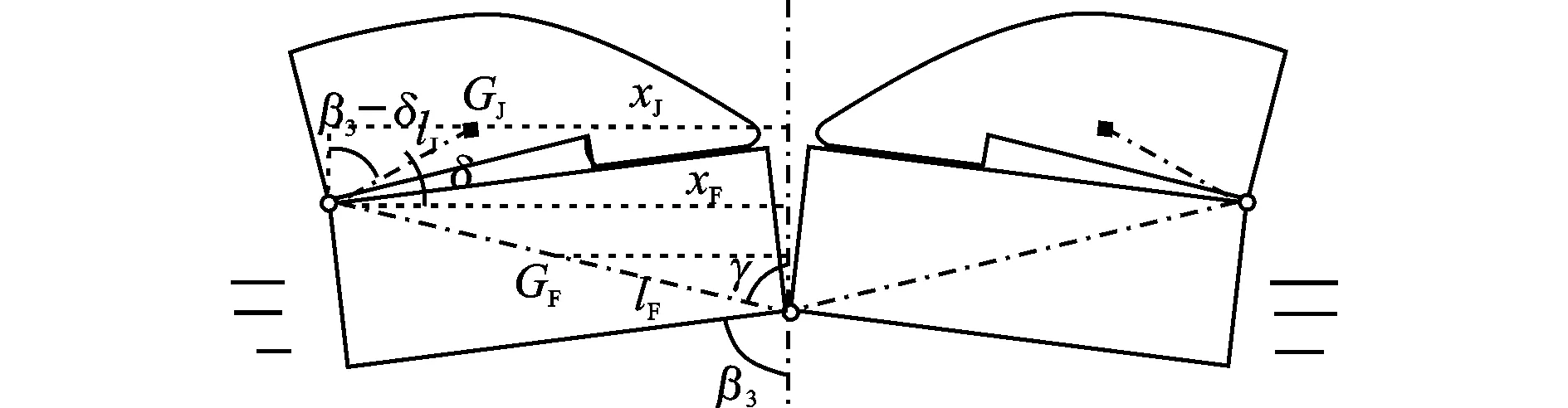
图8 重心位置几何关系图

x1、x2的几何关系如图9所示，其计算分别为

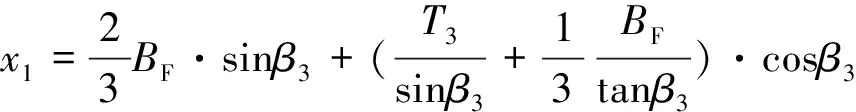
(20)

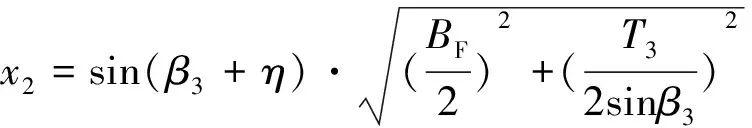
(21)

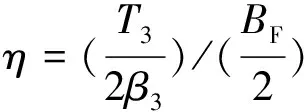
(22)

联立式(14～22)便可求得β3、T3。

图9 浮心位置几何关系图

接下来，重点分析尖舟在阶段二中随着翻转角度的变化时外力矩(不包括扭力杆扭矩)的变化规律。

翻转角度β从0°增大至β1的过程中，尖舟受到的外力矩可表达为

MWII-1=FJII-1·xJII-1+GJ·lJsin(β-δ)

(23)

式中：FJII-1为尖舟受到的浮力，xJII-1为浮心至铰点的水平距离。分别为

FJII-1=ρgL(SJII-R-SJII-T)

(24)

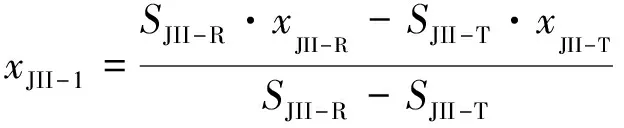
(25)

式中：SJII-R为图10所示矩形面积，SJII-T为图10所示三角形面积，xJII-R为图10所示矩形形心至铰点水平距离，xJII-T为图10所示三角形形心至铰点水平距离。其计算分别为

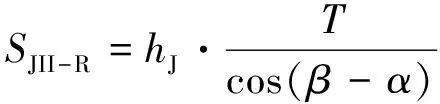
(28)

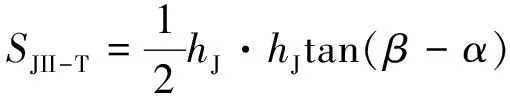
(29)

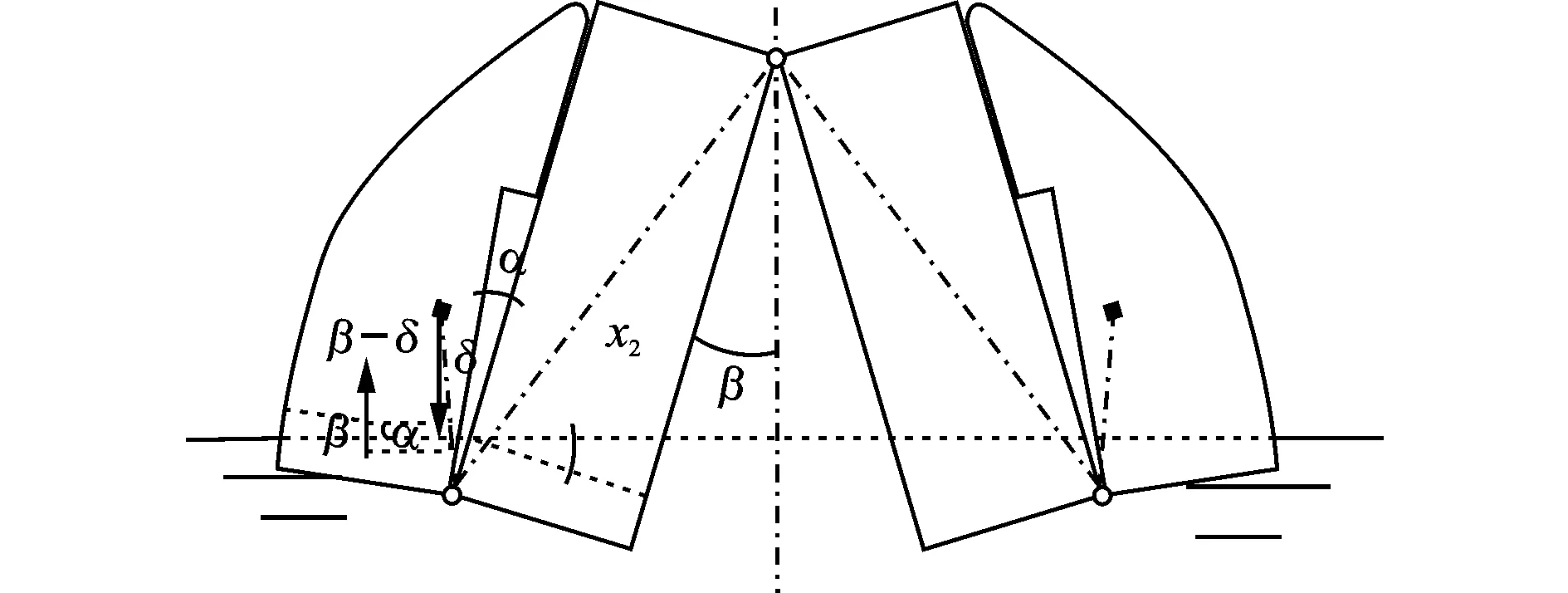
图10 β从0°增大至β1过程中受力简图

在式(23～29)中，存在2个相关的未知变量β和T，二者的对应关系可根据力的平衡条件得出。

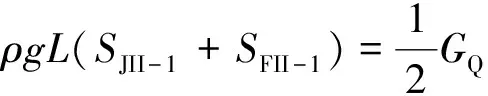
(30)

式中：SJII-1为尖舟端部浸水面积；SFII-1为方舟端部浸水面积。分别为

SJII-1=SJII-R-SJII-T

(31)

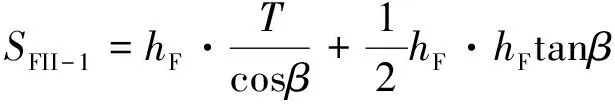
(32)

翻转角度β从β1增大至β2的过程中，尖舟受到的外力矩可表达为

MWII-2=FJII-2·xJII-2+GJ·lJsin(β-δ)

(33)

式中：FJII-2为尖舟受到的浮力，xJII-2为浮心至铰点的水平距离。分别为

FJII-2=ρgLSJII-2

(34)

式中：SJII-2为尖舟端部浸水面积。可由式(36)计算。

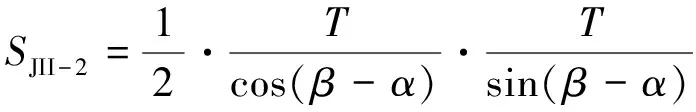
(36)

在式(33～36)中，存在2个相关的未知变量β和T，二者的对应关系可根据力的平衡条件得出。

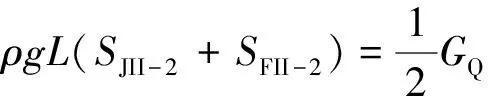
(37)

式中：SFII-2为方舟端部浸水面积。可由式(38)计算。

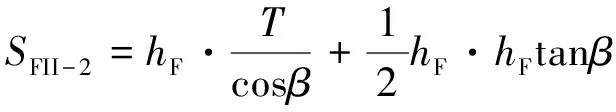
(38)

翻转角度β从β2增大至β3的过程中，尖舟受到的外力矩可表达为

MWII-3=GJ·lJsin(β-δ)

(39)

2.3 阶段三

在此阶段，尖舟受到的外力矩可表达为

MWIII=GJ·lJsin(β3-δ)

(40)

3 模型求解

模型求解步骤如下：

(1)求解确定阶段一的MWI。首先，输入各已知参数；然后，通过式(1～4)求解T，通过式(5～9)求解xf，通过式(10)求解FJI；最后，通过式(11)求解MWI。

(2)求解阶段二3个不同状态的β1、β2、β3。首先，通过式(12)求解β1；然后，通过式(13)求解β2；最后，通过式(14～22)求解β3。

(3)求解[0，β1]区间内MWII-1-β曲线，并确定max{MWII-1}。首先，通过式(30～32)求解每个β值对应的T值；然后，通过式(24～29)求解每个β值对应的FJII-1值和xJII-1；最后，通过式(23)求解每个β值对应的MWII-1值，并确定max{MWII-1}。

(4)求解[β1，β2]区间内MWII-2-β曲线，并确定max{MWII-2}。首先，通过式(36～38)求解每个β值对应的T值；然后，通过式(34～36)求解每个β值对应的FJII-2值和xJII-2；最后，通过式(33)求解每个β值对应的MWII-2值，并确定max{MWII-2}。

(5)求解[β2，β3]区间内MWII-3-β曲线，并确定max{MWII-3}。通过式(39)求解每个β值对应的MWII-3值，并确定max{MWII-3}。

(6)求解确定阶段三的MWIII。通过式(40)求解MWIII值。

4 算例验证

为了验证以上计算模型的有效性，以79带式重型舟桥为算例。表1所列为相关参数。

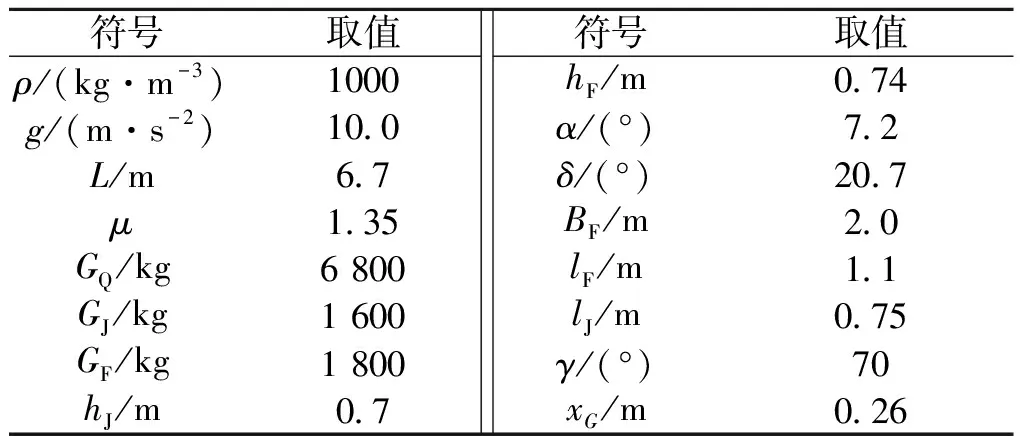
表1 79带式舟桥相关参数

根据模型求解流程，求得尖舟泛水展开过程中受到的外力矩如图11所示。尖舟在阶段一、阶段二状态1、阶段二状态2、阶段二状态3和阶段三受到的外力矩分别为4 996、3 304、7 865、9 941和9 941 N·m。

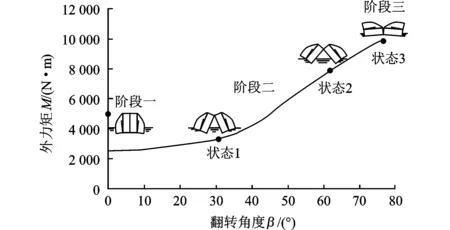
图11 泛水展开全过程尖舟所受外力矩曲线图

从图11可以看出，当尖舟离开水面后，其受到的外力矩随翻转角度的增加，增大得越来越快。因此，在结构设计时，应确保尖舟在阶段二状态1之前打开。从计算结果看，阶段二状态1之前尖舟所受外力矩最大为4 996 N·m，因此扭力杆需提供最小扭矩为4 996 N·m，79带式重型舟桥扭力杆的设计扭矩大小为5 400 N·m，二者比值为1.08。

在尖舟展开过程中，扭力杆除了最大扭矩需大于尖舟所受外力矩外，在打开过程中的任一时刻，其存储的扭矩都需大于该时刻尖舟受到的外力矩。图12所示为79带式重型舟桥在泛水展开过程中，扭力杆存储扭矩和尖舟所受外力矩随翻转角度的关系。可见，在阶段二状态1之前，扭力杆任意翻转角度下存储的扭矩均大于尖舟所受外力矩，从而确保尖舟顺利打开。

图12 扭力杆存储扭矩与尖舟所受外力矩关系图

5 结论

本文针对带式舟桥河中舟扭力杆受力计算缺乏理论计算方法的现状，采用理论推导的方法，建立了泛水展开过程中扭力杆受力的理论计算模型。通过79带式重型舟桥数据，验证了理论计算模型的有效性和准确性，可为扭力杆结构设计提供理论依据。利用本文建立的计算模型，通过合理地调整设计参数，能够确保尖舟在较大角度范围内都能够打开，从而实现舟体的顺利泛水展开。