基于深度强化学习的卫星动态功率控制技术

徐素洁， 胡 欣， 王 银， 王丽冰， 马仕君， 王卫东

(北京邮电大学 电子工程学院，北京 100876)

高通量卫星作为国家信息网络的重大基础设施，以其覆盖范围广、通信质量好、运行维护费用低等特点，在保障国计民生等领域发挥着不可替代的作用[1]。随着用户数量和数据业务的显著增长，人们对其提供业务的多样性和服务质量等方面提出了更高的要求。面对信息的爆发式增长，高通量卫星不可避免地存在星上资源受限的特征，具体表现在频谱资源、功率、计算和存储资源上。智能自主以及灵活高效地对高通量卫星通信系统的可用信道和功率进行动态分配，对提升卫星的通信能力和资源利用率具有重要意义。

在功率分配方面，目前针对高通量多波束卫星系统功率分配研究主要包括固定分配和动态分配两方面。传统的卫星系统在功率分配方面多采用固定分配方式[2]，但是这种方式难以适应实际通信场景中通信需求量的动态性，极易造成资源的浪费。为了克服固定分配的缺点，各种动态功率分配算法[3-7]应运而生。文献[3]指出，未来移动行业中用户需求量昼夜变化大，为满足动态的需求变化，许多高通量卫星将具备灵活的功率和带宽分配功能。大量可调的卫星参数可以保证用最少的资源来满足需求，特别是涉及高维问题，手动分配资源变得更加不切实际。因此，研究动态卫星功率分配算法显得尤为重要。文献[4]提出最大化系统容量算法，即注水算法，该算法实现功率自适应分配的同时实现总的数据传输速率最大化，但并未考虑各波束间功率资源分配的公平性以及业务优先级。Hong等[5]提出将动态功率分配问题建模成一个约束条件为非线性函数的优化问题，兼顾公平性和系统总容量，并通过拉格朗日乘数法对该优化问题求解。而在多波束卫星系统中分配资源以满足流量需求的问题被证明是NP-hard和NP-hard近似问题, 文献[6]为启发式算法提出了通用的理论框架，在存在系统功率约束的情况下，将问题分解成基于颜色的子问题，降低了相关复杂性，使该资源分配方法切实可行。文献[7]的研究结果表明，尽管基于元启发的方法在解决功率和带宽分配问题上具有不错的效果，但这些算法并没有实时处理能力。

为了将人工智能赋能于卫星通信场景，北京邮电大学空天地智能感知与通信研究所将深度强化学习(Deep reinforcement learning，DRL)框架引入卫星通信的无线资源管理领域，为低复杂度实时动态地实现无线资源管理提供了全新的解决思路[8]。由于功率的控制维度可以分为连续量控制和离散量控制，传统的深度强化学习框架可以满足离散量功率控制的技术需求，而不能直接应用于连续量功率控制场景。在文献[8]的基础上，麻省理工学院系统架构实验室提出一种基于深度强化学习的近端策略优化框架，可实现对卫星功率的连续量控制[9]。然而，这种方法没有考虑卫星场景中的同频干扰问题，在流量需求较低时效果不佳。文献[10]提出了一种基于深度强化学习的抗干扰算法，可以获得最优的抗干扰策略，该方法仅依赖局部观测信息，应用范围更加广泛。

鉴于无线场景的复杂性，无模型的深度强化学习更能满足多波束卫星的技术需求。因此，本文利用无模型的强化学习方法，提出一种基于深度强化学习的近端策略优化方法，通过使用神经网络对策略进行建模，实现状态与动作之间可行的映射，合理化状态、收益的设计，使智能体完全根据过去经验不断改进策略，实现策略优化。该方法可较低复杂度地动态控制高通量卫星各波束的功率分配，满足卫星请求容量和功率有效利用率的多优化目标需求。

1 系统模型与问题公式化

1.1 系统模型

本文考虑了一种运行在Ka频段的高吞吐量多波束卫星系统。多波束卫星系统通过多波束天线，产生多个点波束覆盖地面区域。为突出资源分配中功率控制的优化问题，假设馈线链路为无噪声的，并将下行信道建模为加性高斯白噪声(AWGN)信道。为了在每个波束上实现灵活的功率分配，假设卫星有效载荷配备了必要的模块，例如多端口放大器(MPAs)、行波管放大器(TWTAs)。多波束卫星通信系统可以通过波束间的频率复用来提高频谱效率。假设信道分配方式为固定频分复用，频率复用因子为4，图1描述了多波束卫星通信。不过，多波束场景适用于任何形状、大小的波束以及任何频率复用模式。

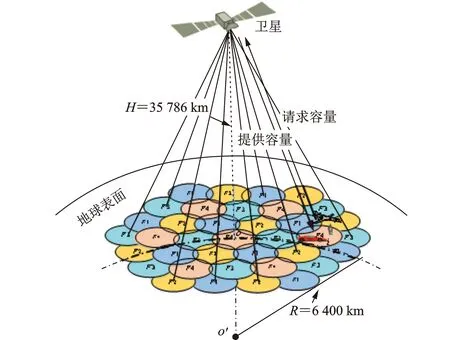
图1 多波束卫星通信示意图

卫星在地面上的多波束表示为B={n|n=1,2,…,N}。功率控制属于资源分配问题，通常资源分配还包括带宽分配。通过四色复用，总可用下行带宽Btot平均分布在4种颜色中，每一颜色的可用波束带宽为Btot/4。除了每个波束功率分配外的载波分配，假设每一波束传输的M个载波，并平均共享每一颜色的可用波束带宽，其中一个载波表示用于传输数据流的基本频谱实体，载波带宽Bc=Btot/(4M)。以上假设将系统可用带宽Btot通过频率复用并在波束和载波之间进行了分配，信道资源相互正交，提高了信道利用率。

下面对系统总可用功率Ptot进行合理分配，使不同波束的比特速率满足各自的流量需求。定义每个波束的功率分配矢量为Pb

Pb=[Pb,1,Pb,2,…,Pb,M]

(1)

式中：Pb,c为分配给b波束载波c的功率，其中b=1,…,N；c=1,…,M，以波束为基础的功率分配矩阵P表示为

(2)

然而，实际中波束转发器的所有载波都由同一个放大器放大，因此对给不同载波分配的功率电平的范围设置了限制。在假定的情形下，放大的载波输出功率平均地分给带宽相等的载波(Bc)，因为载波的功率与它的带宽成比例。因此，采用等功率载流子共享总波束功率。假定波束功率分配不均匀，同时每个波束载波功率分配均匀，载波发射功率Pb,c=Pb/M。最后用Pb(OBO)表示波束b的发射功率与所需输出功率回退(Output back off，OBO)的关系。

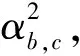
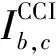
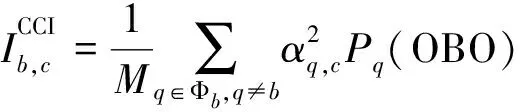
(3)

由此可以计算出波束b内载波c覆盖范围内的终端接收的信干噪比(Signal to interference plus noise ratio，SINR)，SINR的计算由DVB-S2采用的自适应编码和调制方案的总频谱效率决定。由于波束增益和传播信道条件在覆盖范围内的变化，每个终端都有不同的SNIR值，如式(4)所示。

(4)

式中：N0为噪声功率谱密度。它依赖于接收机天线和等效噪声温度以及覆盖区域上的气候条件，因为噪声温度会因降雨衰减而加剧。再根据香农定理得到位于波束b的接收载波c在信道(Bc)上的信道容量，如式(5)所示。

Cb,c=Bclog2(1+SINRb,c)=

(5)

1.2 问题公式化

首先，针对波束间业务量分布不均匀的问题提高多波束卫星系统的资源利用率，以满足流量需求的同时最小化系统功耗为目标，完成功率资源分配。当优化变量为载波功率Pb,c时，则要满足

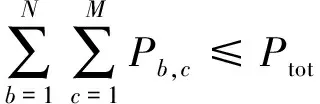
(6)

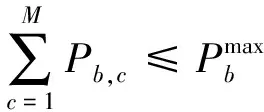
(7)

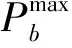
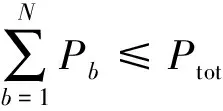
(8)

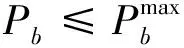
(9)

优化目的是确定满足各自流量需求的波束功率级Pb，同时使直流功耗最小。在有限的功率资源情况下，在较短的时间内最佳地分配这些资源，降低总体未满足系统需求(Unsatisfied system capacity ratio, USCR)和溢出系统需求的和(Overflow system capacity ratio, OSCR)分别为

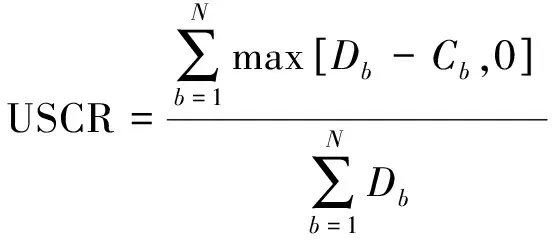
(10)

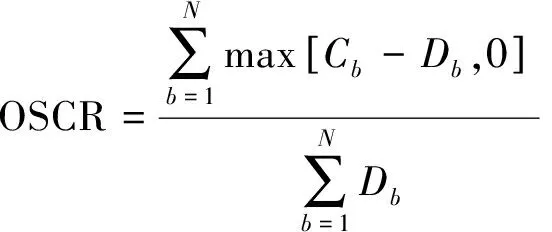
(11)

式中：Cb表示波束b提供的信道容量，Db表示波束b的流量需求。

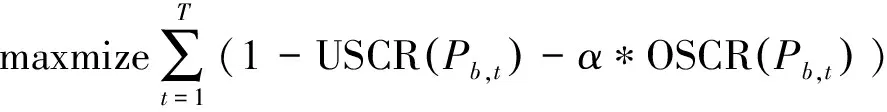
(12)

(13)

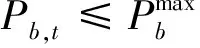
(14)

Pb,t≥0 ∀b∈B

(15)

式中：B为卫星的波束集合。

式(12)为多波束卫星通信系统中动态功率分配的最优化目标,其中α为加权常数，用于定义两个目标之间的优先级。式(13)表示每个波束分配的功率不应超过单波束功率限制。式(14)表示波束总发射功率不应超过卫星的机载总功率。每个终端的下行容量，与分配的带宽、功率、发射天线增益以及接收天线增益相关。当终端位置确定时，可以通过调整带宽、功率分配方式来调整信道容量。本文通过调整各波束分配的功率调整信道容量，在满足系统需求的同时最小化系统功耗。

2 深度强化学习算法

作为机器学习的一种，强化学习在智能体与环境交互的过程中，通过环境的反馈提升自身决策能力。强化学习算法流程框图如图2所示。

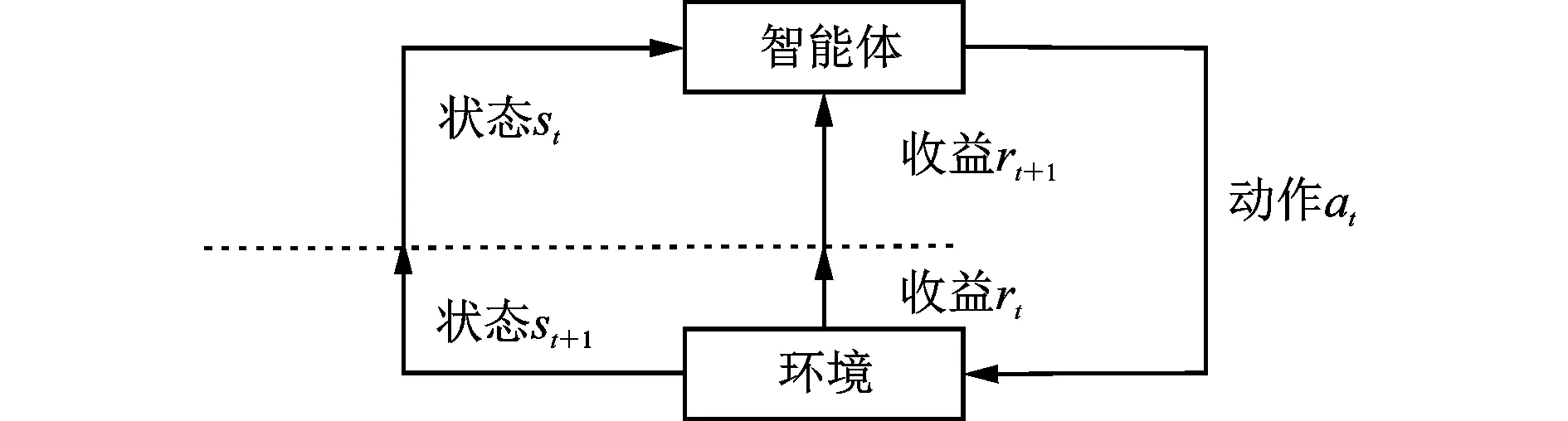
图2 强化学习算法框图

基本的强化学习架构由两个基本要素组成：智能体和环境。给定状态st表征某个时间步t的环境状态，智能体的目标是采取将累计收益Gt最大化的动作at，定义为

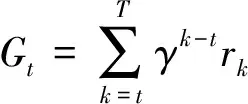
(16)

式中：T为episode的长度，rk为在时间步k获得的奖励，γ为折扣因子。

深度强化学习研究目前正处于快速发展阶段，其涉及的算法有基于值函数的深度Q网络及相关改进算法和深度确定性策略网络、基于策略的近端策略优化算法以及异步优势动作评判算法，还有同时训练多个任务的无监督辅助强化学习。

2.1 近端策略优化(Proximal policy optimization，PPO)算法

PPO算法是2017年由Open AI提出的一种DRL算法[11]。深度强化学习方法选用目前最先进的近端策略优化算法，PPO 算法是策略梯度(Policy gradient)方法的一种改进算法。策略梯度算法作为基于策略的优化方法，与基于值的优化方法相比更适合应用在具有连续的状态动作空间的问题中。

策略梯度方法对于训练步长的选择十分敏感，过大或过小的步长均会造成非常差的结果，而PPO 算法的提出解决了训练步长难以确定的问题。在PPO算法中，通过限制每步策略更新的大小消除这种缺陷，使用clip 代理函数和自适应kl惩罚和限制每次迭代时策略的更新大小。PPO 能够在易于实现、样本复杂度和易于调整之间实现平衡，对于连续控制问题有很好的性能，稳定性和收敛性的优势使得PPO成为Open AI主推的深度强化学习方法。

2.2 DRL架构

图3显示了针对多波束卫星动态功率分配的DRL架构。本文使用PPO算法的策略梯度方法改进分配策略。PPO算法通过与环境交互采样数据，并使用随机梯度上升优化“替代”目标函数。由于该算法不允许对策略进行较大的连续更改，因此可以防止在某些情况下策略性能明显变差的问题，使系统更加稳定。

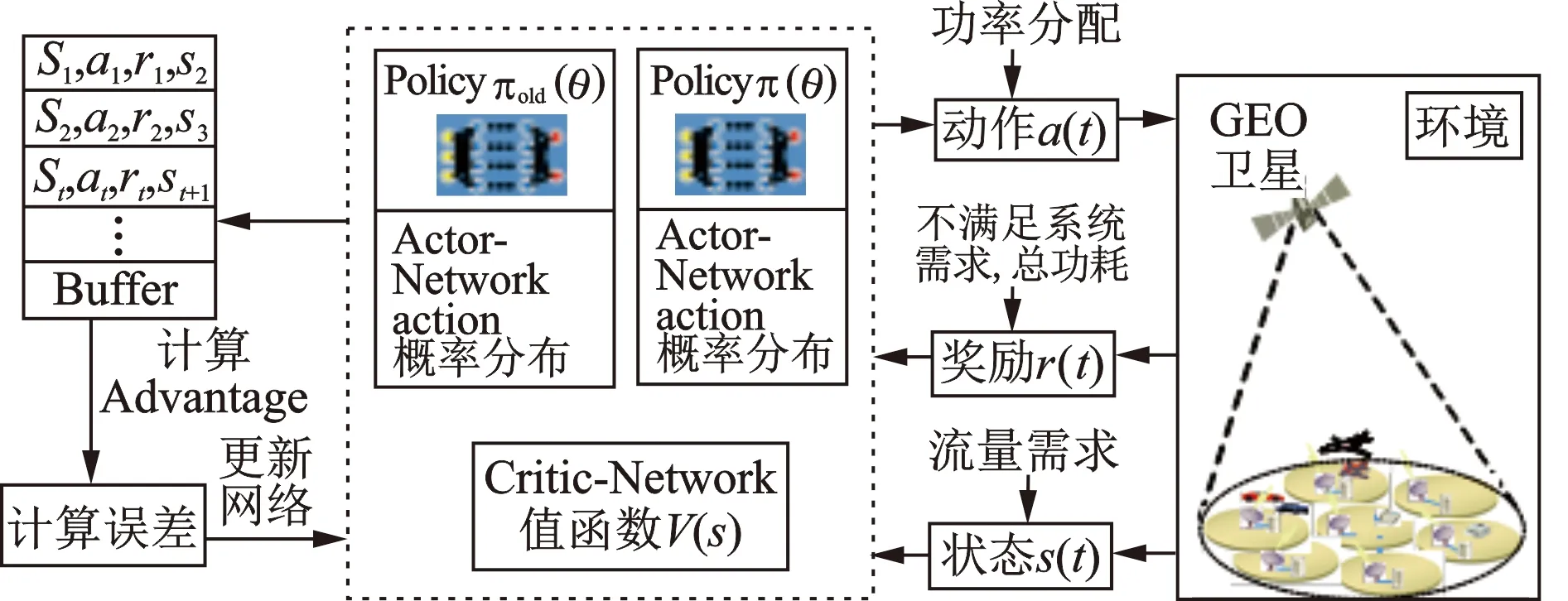
图3 DRL架构

本文通过神经网络给出功率分配策略。神经网络是一种基于大脑神经结构的非线性计算模型，能够学习执行分类、预测、决策和可视化等任务。由人工神经元组成的人工神经网络组成3个相互连接的层：输入层、隐藏层和输出层。在训练阶段，神经网络通过反向传播作为一种有效的学习算法来计算损失函数的梯度，并调整每个神经元的权值。如图3所示，神经网络是对于Actor网络和Critic网络分别进行训练。状态分别输入到Actor网络和Critic网络，图中的Policy和Old policy都是Actor网络。Old policy由Policy在训练完一个批次后进行更新。

图3中的环境由卫星系统以及每个波束的流量需求组成，是与问题相关且智能体无法直接控制的内容。智能体即卫星根据环境状态进行功率分配，即策略分配，根据环境状态选择动作，以及策略优化算法，该算法根据过往经验不断改进分配策略。功率分配中，连续变量为每束波束的流量需求以及分配给波束的功率值，因此不同的环境状态和执行动作的数量是无限的。在这种情况下，在分配策略中存储每一个状态的最佳动作是不切实际的，因此本文使用神经网络对策略进行建模，在输入状态和输出动作之间实现可行的映射。

2.2.1 状态

在卫星总功率有限的情况下，波束通过选择合适的传输功率来克服共信道干扰和降雨衰减的影响，满足当前的流量需求。该决策变量基于当前时刻t波束需求Db与上一时刻波束提供容量Ct-1的差值。因此，状态只与当前时刻的流量需求状况和上一时刻的动作，即上一时刻的功率分配情况有关，将状态表示为

st=(Dt-Ct-1)

(17)

2.2.2 动作

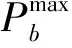
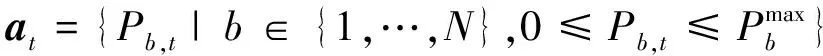
(18)

2.2.3 收益

收益的设计需要综合考虑未满足系统需求的比例USCR和溢出系统需求的比例OSCR, 通过α权重的设计，可以保证在满足波束流量需求的前提下，使提供容量可以略大于流量需求。波束内的信道容量越接近于流量需求，rt越接近于1，表征该状态较好，反之表征该状态较差。

Reward=1-USCR(Pb,t)-α*OSCR(Pb,t)

(19)

式中：Cb,t表示t时刻波束b提供的信道容量，Db,t表示t时刻波束b的流量需求。

2.2.4 下一时刻状态

下一个状态是在时间步t+1观察到的波束环境，该环境由时间步t中所有波束的动作确定。此外，通过对Reward范围进行判断，实现流量需求的变化。当Reward处于设定的较好的范围内时，流量需求跳转到下一时刻；当Reward不能满足当前规定范围时，流量需求不改变，直至Reward达到较好的值，此时状态的改变直接由上一时刻的动作决定。

2.3 算法实现

算法实现流程主要分为初始化、训练更新和性能评估统计3个阶段，其中初始化阶段进行卫星场景参数的初始化，以及PPO学习率等参数以及Actor及Critic网络的初始化，在功率资源初始化阶段，多波束卫星星上总功率平均分配给各波束。训练更新阶段，根据卫星通信系统中各波束用户通信业务请求情况以及系统中可用功率资源，完成功率动态分配的马尔科夫决策过程(Markov decision process， MDP)，进行功率分配策略的学习更新。最后在指定的训练周期内，绘制出训练期间内性能指标变化的曲线图，以及对最后流量需求和提供的信道容量的柱状图进行对比，对智能体学习到的动态功率分配结果进行性能统计。下面对3个阶段具体说明。

(1)初始化阶段

① 初始化卫星通信场景相关参数，工作频段、系统带宽、功率谱密度等。

② 初始化PPO算法的相关参数，运行周期，每周期训练次数，Actor和Critic网络的学习率等。

③ 统计系统中各波束覆盖情况以及波束的流量需求。

(2) 训练与更新阶段

① 每周期内进行重置以及经验Buffer。

② PPO内Actor网络根据当前状态st选取动作at。

③ 环境根据选区的动作以及当前状态更新状态并返回下一状态，收益和平均通信满意度。

④ 储存经验条目st,at,rt到经验池。

⑤ 如果训练次数等于训练批次，则计算优势函数、经验池内数据与新网络重置经验。

(3) 性能评估

根据每个周期内计算的周期平均收益、周期平均通信满意度绘制曲线图。

3 仿真结果分析

本文的仿真平台为Python3.6.0。在多波束卫星通信系统中，地球同步轨道(Geosynchronous earth orbit，GEO)卫星各波束间业务量非均匀分布，终端用户利用所分配的带宽、功率等资源与GEO卫星进行通信，并根据各用户下行容量计算系统容量，将各方案进行对比。

(1)仿真参数设计

在考虑的GEO多波束卫星功率分配仿真场景中，卫星处于Ka波段，工作频段为20 GHz，产生N=37个点波束覆盖地面区域，表示为B={n|n=1,2,…,N} ，可用总带宽为Btot=500 MHz，可用总功率Ptot=2 000 W。表1为多波束卫星动态功率分配系统的仿真参数。近端策略优化(PPO)算法参数的设置如表2所示。

(2)仿真结果

本文使用系统一日服务作为参考，每一小时对系统流量请求进行采样并对37波束动态功率分配。随着时间的变化，实际的业务量分布是不均匀的。图4显示了一天中流量变化的假定曲线。如图所示，一天的流量高峰时段是上午7:00～9:00和下午14:00～18:00左右，而清晨和深夜是流量需求相对较低的时间段。

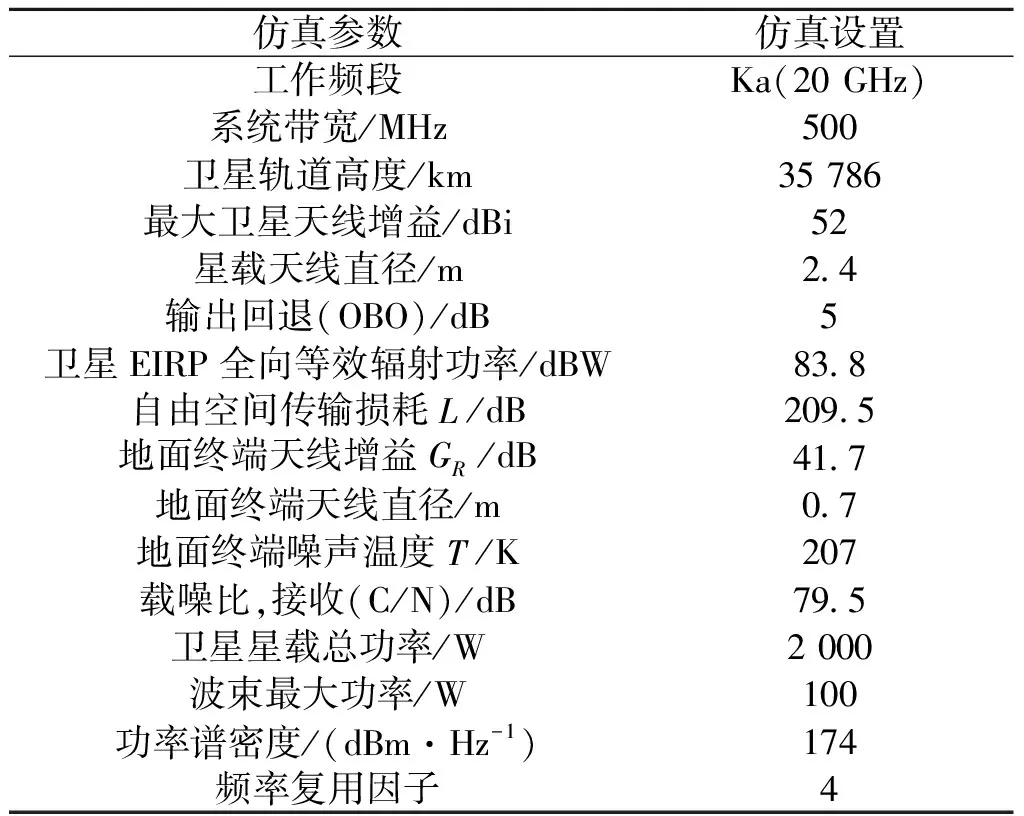
表1 动态功率分配场景仿真参数

表2 PPO算法参数设计

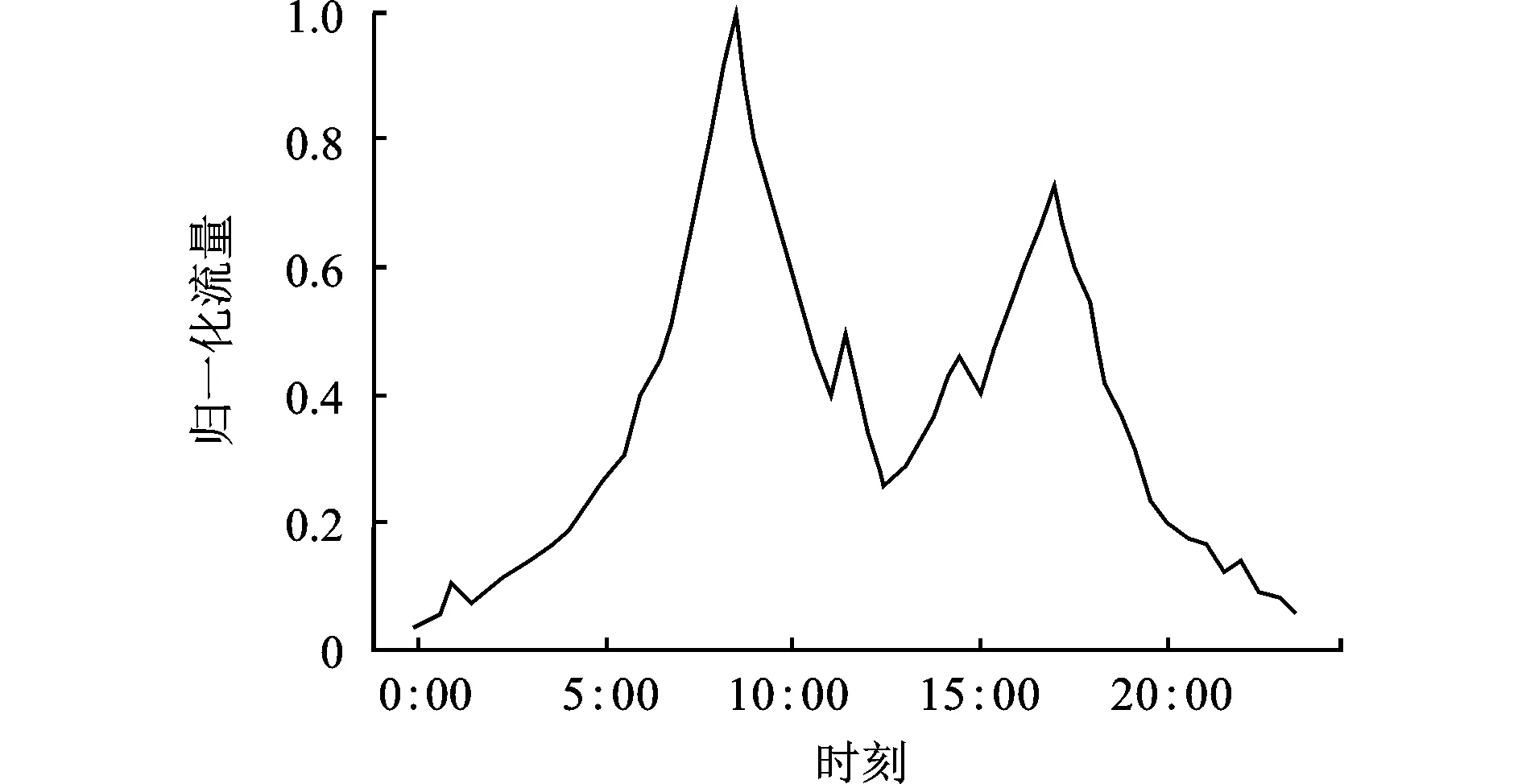
图4 24小时流量需求变化图

为了更好地理解所提算法的优势，在图5～8中分别将4个不同时刻包括高峰、非高峰的请求流量与提供容量进行了对比。

图5～8中，蓝色矩形代表流量需求，绿色矩形代表提供的信道容量。可以看到流量需求较低时，各波束均能满足终端的流量需求；流量需求较高时，分配的功率可以满足大多数波束的流量需求。仿真结果表明，该算法能够灵活地分配功率资源，功率资源利用率更高。

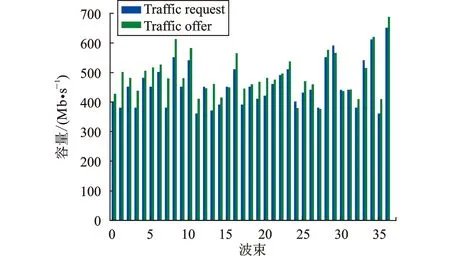
图5 12:00时流量需求与提供容量

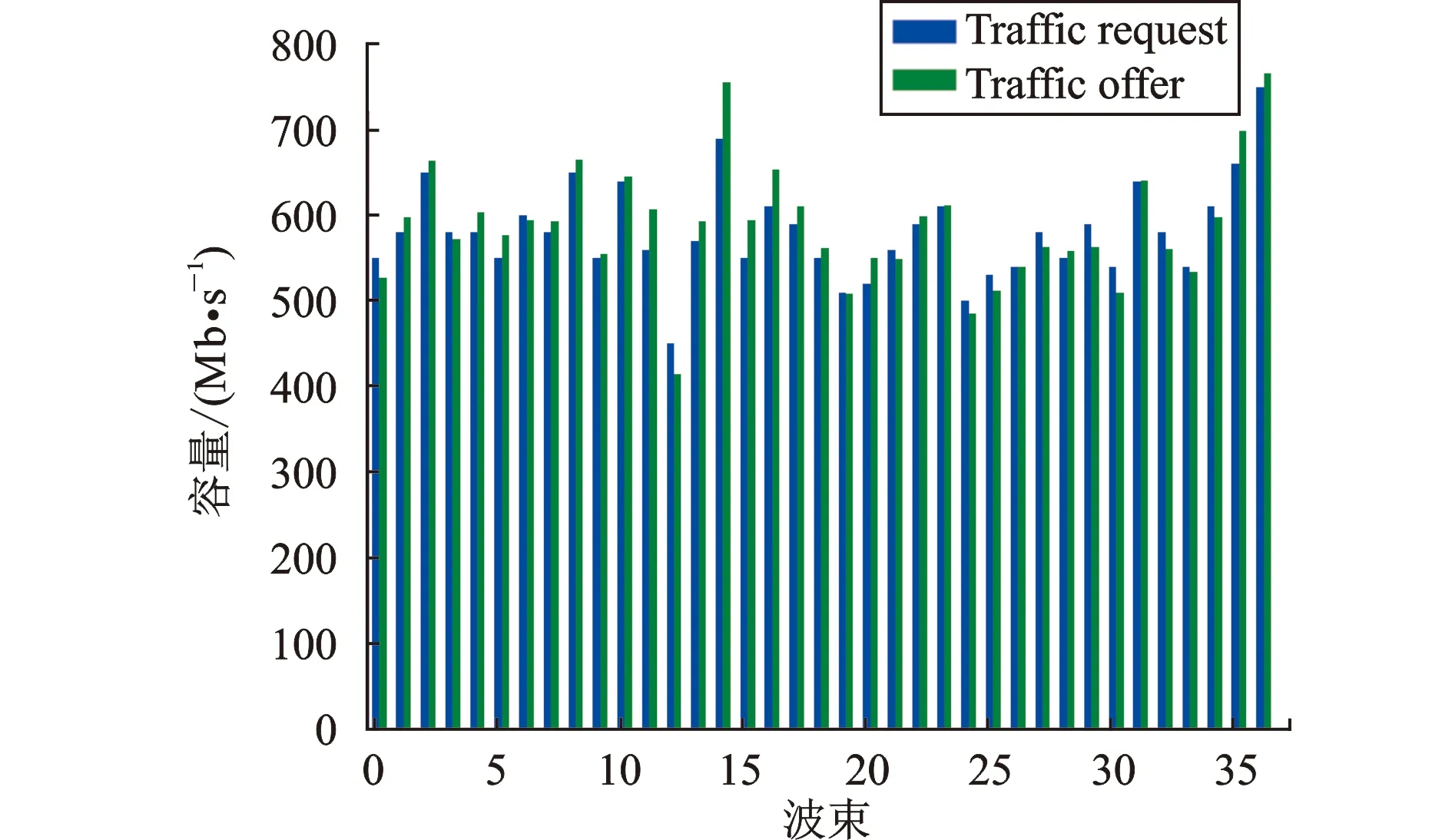
图6 5:00时流量需求与提供容量

图7 9:00时流量需求与提供容量

图8 18:00流量需求与提供容量

收益随时间变化情况如图9所示，未满足系统需求与溢出系统需求的和USCR+OSCR随时间变化情况如图10所示。

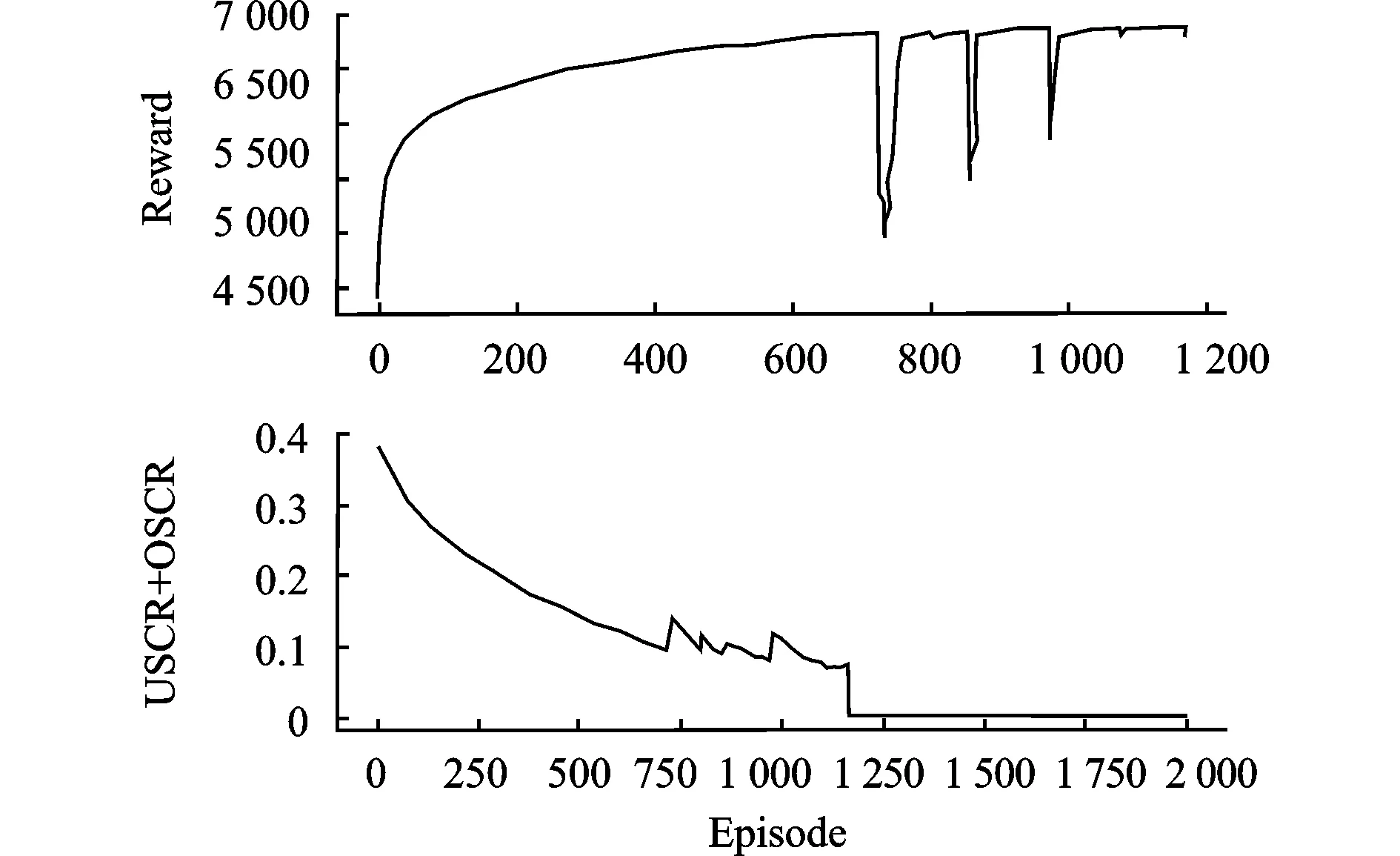
图9 Reward、(USCR+OSCR)收敛图

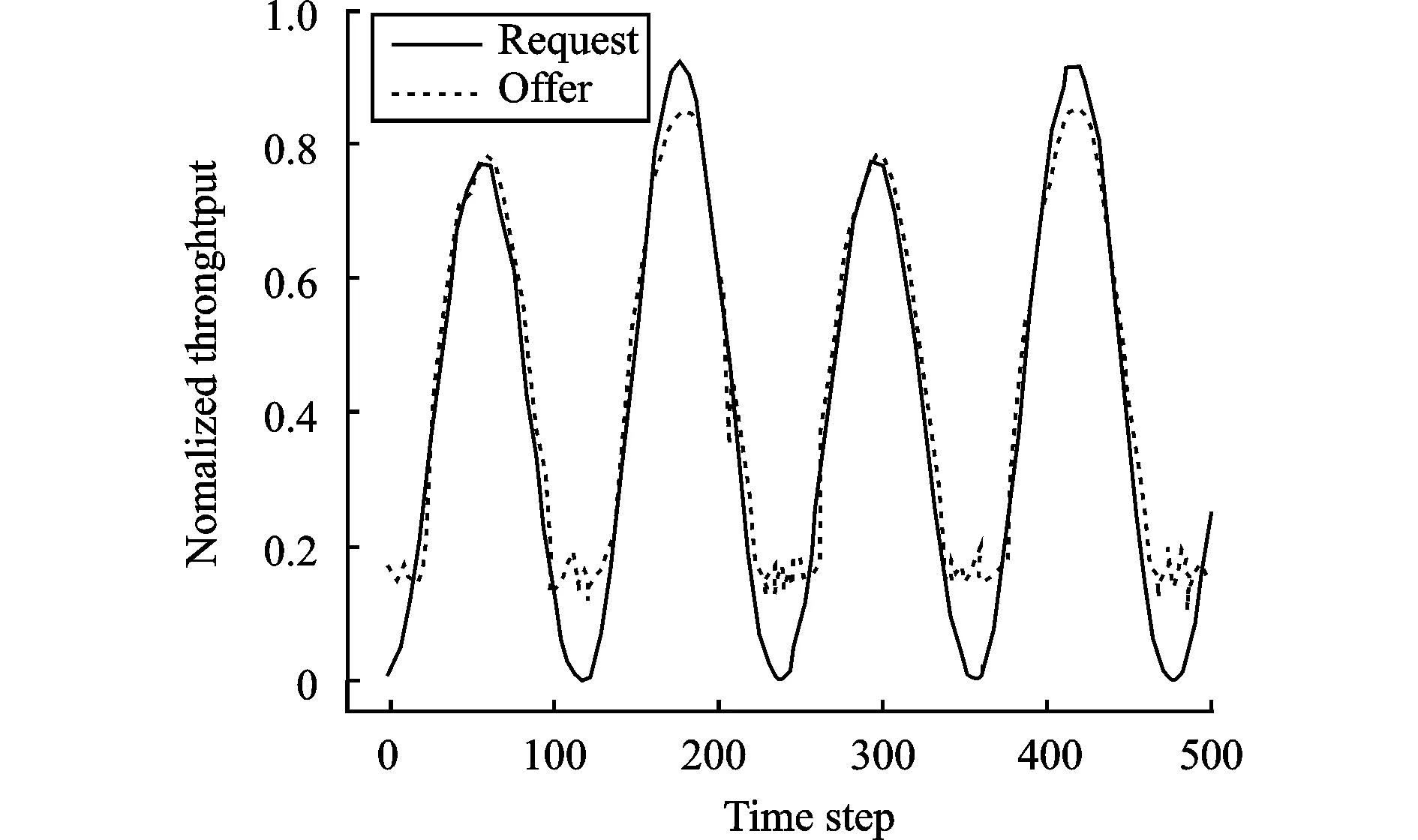
图10 48小时需求与提供容量对比

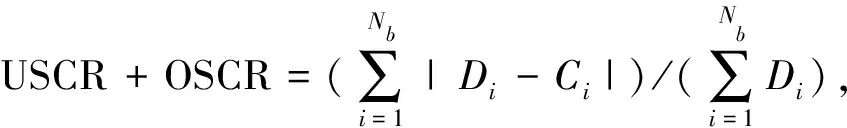
图10为48小时归一化后的流量需求与提供容量对比，与文献[8]相比，提供容量不仅对峰值需求产生响应，当需求量较低时，智能体也能为波束分配合理的功率，减少卫星资源的浪费。此外，由于卫星通信有较大的时延，训练网络放在地面端，并将训练好的输入和输出数据集在卫星端引入深度学习，生成一个可以直接感知状态并输出功率的深度学习网络。图11为Loss曲线收敛图，输入一个流量需求，深度学习网络可以马上生成对应状态的功率。

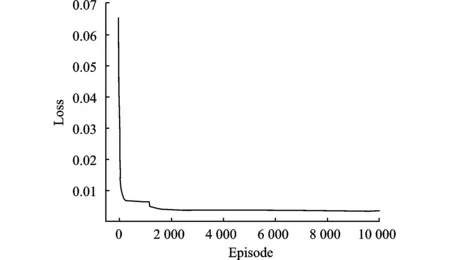
图11 Loss曲线收敛图

4 结论

本文提出并验证了一种基于策略的近端策略优化算法的卫星功率动态控制方法。实验结果表明，基于近端策略优化算法的卫星动态功率控制方法表现出不错的性能，能较好地处理实际的流量需求，并给出不同波束的最优功率分配值。同时，本文对卫星功率分配系统模型做了较全面的分析，为后续研究更加贴合实际的卫星场景打下了基础，但是本文所实现的内容还有不足，后续需要对DRL架构进一步完善，并进一步验证智能体的泛化能力。