延迟CSI反馈下的协作NOMA系统用户选择方法

殷志远， 陈 瑾， 李国鑫， 王海超

(陆军工程大学 通信工程学院，江苏 南京 210007)

随着现代通信的蓬勃发展，频谱资源日益稀缺。为了高效利用有限的频谱，非正交多址接入(NOMA)技术被广泛研究[1-3]，其核心思想是多个用户能够在同一频段内以不同功率同时通信，从而节约频谱资源。

在下行NOMA研究领域，一个重要的方向是协作NOMA，文献[4]设计了一个经典的协作NOMA策略，其中协作用户成功依次解码其他用户的消息并转发，从而帮助其他用户通信。文献[5]将协作NOMA用户的中继选择策略分为两步，实现最大的分集增益。文献[6]从公平性角度出发，设计了连续用户中继方案，进一步高效利用频谱。文献[7]为用户中继协作NOMA网络设计了两种不同转发方式的传输协议，并推导了系统中断性能的表达式。文献[8]在存在用户中继译码误差的条件下研究了协作NOMA网络在瑞利衰落信道中的中断性能，并为系统设计提供了一些有用的见解。在上述协作NOMA研究中，信道状态信息(CSI)都是即时反馈的，然而实际通信中，CSI反馈存在延迟，接收到的信道信息是过时的。CSI的反馈延迟会导致系统错误解码，中断性能严重下降。文献[9，10]研究了正交多址接入网络中信道信息反馈延时系统的中断性能，表明过时的CSI会将系统分集增益降到最低，无论CSI精度如何，存在反馈延迟时分集增益始终为1。在协作NOMA系统中，若CSI反馈延迟，其空间自由度的优势将不复存在。然而，现阶段对协作NOMA网络中CSI反馈延迟问题的研究不足。文献[11]研究了过时CSI下协作NOMA部分中继选择系统的性能，但该工作中节点未考虑解码转发协议，没有给出合理的中继选择策略，也没有提出提升系统性能的方法。基于以上考虑，有必要对CSI反馈延迟的协作NOMA网络进行深入研究。

近年来，深度学习(DL)在通信领域得到了广泛应用，其中大量研究聚焦于将DL与信道估计技术相结合[12-16]，而与过时CSI相关的研究较少。为了降低CSI反馈延迟带来的影响，现有研究采用DL技术对迟滞的CSI进行处理，利用深度神经网络的预测能力提升通信性能。文献[17]对车联网系统中CSI延迟反馈条件下的功率分配问题进行了研究，提出了基于循环神经网络(RNN)的预测功率分配算法。然而，文献[17]使用的是标准RNN结构，仅在全连接神经网络的隐藏层中加入一个循环层。相比于门控循环单元(GRU)与长短期记忆(LSTM)，标准RNN结构的预测能力较弱，所得CSI的预测误差较大。文献[18]设计了一个基于卷积神经网络(CNN)的信道预测框架用以解决多输入多输出(MIMO)系统中CSI反馈延迟问题，提高了频谱效率。由于CNN能够提取数据特征，它的预测效果可以媲美标准RNN并减小计算代价，但它对于时间步的顺序不够敏感，会导致预测网络的性能不稳定。上述研究提出的预测网络都有所欠缺，因此，有必要设计性能更好的预测网络来解决CSI反馈延迟问题。

基于上述研究启示，本文将DL技术引入协作NOMA网络以解决CSI反馈延迟条件下的用户中继选择问题。

1 系统模型

本文研究的下行用户中继协作NOMA如图1所示，其中共有一个基站、N个近用户和一个远用户。近用户收到基站发送的消息后，不仅要解码自己的信息，还要充当中继，解码转发远用户的信息，协助远用户通信。基站不与远用户直接通信。

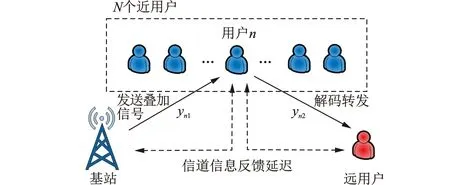
图1 信道信息延迟反馈的下行用户中继协作NOMA

在一个时隙内，用户的通信被等分为两部分。在第一部分，基站首先选择一个近用户(如第n个近用户)，向其发送一个叠加信号yn1，该信号带有所选近用户信息与远用户信息

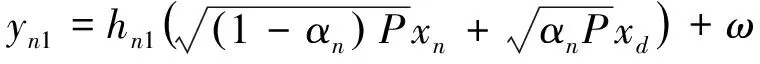
(1)

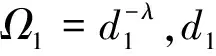
在接收到基站发来的信号后，近用户需要依次解码出远用户的信息和自己的信息。在检测信息处接收到的信干噪比(SINR)分别由以下公式给出

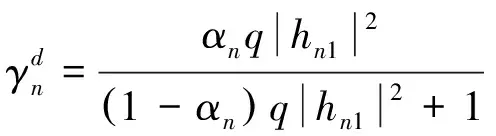
(2)

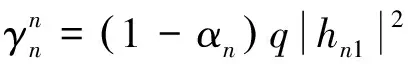
(3)

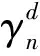
如果近用户成功解码远用户的信息，则在该时隙的第二部分将该信息转发给远用户。假设基站与近用户的发射功率相同(均为P)，此时远用户接收到的信息yn2表示为

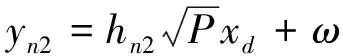
(4)

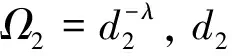
γdn=q|hn2|2

(5)

然而，在实际通信过程中，CSI的反馈是存在延迟的，所得到的信道系数是过时的。过时的信道系数与准确的信道系数可以用如下关系式表示[10]

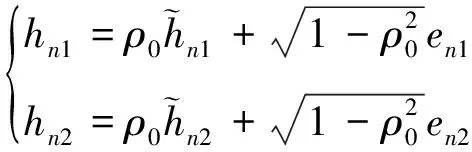
(6)

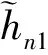
根据式(2，3，5)，远用户与近用户的可达信息速率分别表示为

(7)

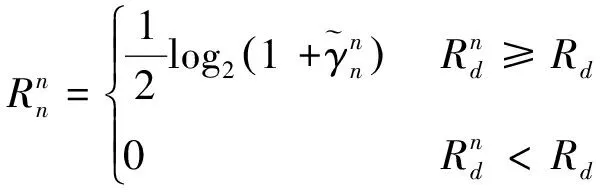
(8)

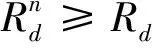
2 用户选择策略与中断性能分析

首先提出一个近用户选择策略，然后基于该策略推导无DL情况下的系统中断概率，最后推导系统分集增益，分析系统中断性能。

2.1 近用户选择策略

所提策略分为两部分：(1) 需要确定功率分配因子以保证近用户成功解码；(2) 需要确定能够达到通信要求的近用户集合，并选择最佳近用户。

2.1.1 功率分配优化

功率分配因子直接关系到近用户选择是否合理。为了确保近用户能够成功解码信息，考虑含有αn的项，根据式(2，7)可得

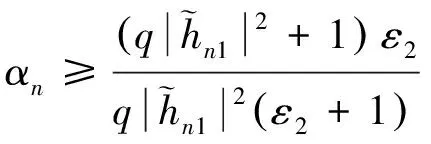
(10)

根据式(3，8)可得

(11)

式中：ε1=22Rn-1，ε2=22Rd-1。仅在功率分配因子αn满足式(10)与式(11)时，近用户才能成功解码出远用户与自己的信息。

2.1.2 最佳用户选择

(12)

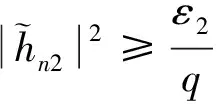
(13)

因此，该集合可以表示为

(14)

为了最大化远用户的可达速率，所选近用户应包含在集合中。因此，最佳近用户可表示为

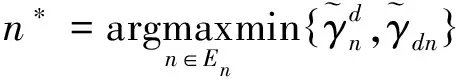
(15)

2.2 系统中断概率

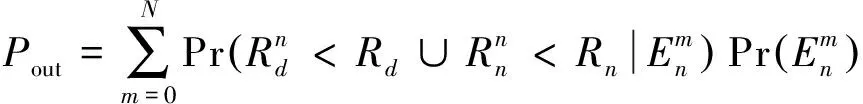
(16)

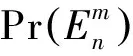
由此可得集合En中有m个近用户的概率为

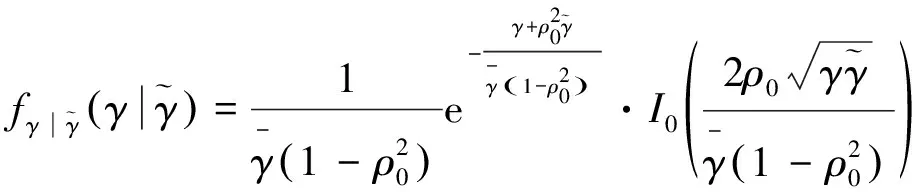
(19)

将式(18，20)代入式(16)，可得系统中断概率为

2.3 渐近性能分析

由于指数函数e-x的泰勒级数展开式为

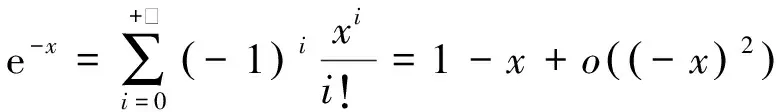
(22)

式中o(·)表示高阶无穷小。因此式(20)可以改写为

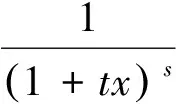
因此可将式(23)改写为

可将式(25)简化为

根据式(22)，可得式(18)的渐近表达式为

将式(27)与式(28)代入式(16)，可得系统中断概率的渐近表达式为

(29)

根据渐近中断概率可以推导系统分集增益。系统分集增益定义为[21]

(30)

在理想状况下，CSI是准确的，分集增益为N。若CSI是过时的，从式(29)中可以观察到中断概率依赖于含有q的项，此时的分集增益为

d=

(31)

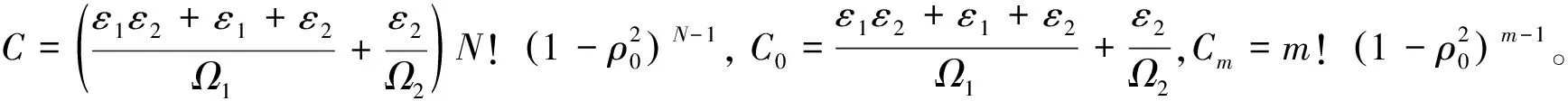
根据上述分析可以看出，CSI反馈延迟使得多用户分集增益消失，严重降低系统中断性能。

3 信道信息预测方法

为了改善由CSI反馈延迟导致的系统性能下降，采用深度学习方法来预测当前CSI信息。准确的信道信息有利于选择更合适的近用户，降低系统中断概率。如式(19)所示，过时的CSI与准确CSI具有相关性，这使信道信息的预测成为可能。

为了准确预测信道信息，神经网络需要大量的数据来进行学习，随着隐藏层的增加，很容易导致梯度消失。GRU层是为了解决梯度消失问题而设计的，类似于LSTM层，可以保存先前学习过的信息以便后面使用。与LSTM相比，GRU的计算代价更低，且更关注近期的数据，更适合用来对迟滞的CSI进行预测。因此，本文设计了带有GRU的深度神经网络。同时，为了提高学习收敛速度，降低输入数据的维度，使用卷积神经网络进行预训练。

3.1 信道信息特征提取

在通信系统中，数据通常表现为传输符号序列SK={s1,s2,…,sK}。如图2所示，输入是复数型的信道数据序列，由于现有的很多深度学习库函数不能对复数域操作进行支持，信道数据序列需要预处理。本文的预处理方式是分离复数的实部和虚部，并组成一个新的数据序列，同时还需提取该数据序列的特征向量。在提取序列的特征向量时，一维CNN表现出了优异的性能，它可以提取高级特征，缩短序列长度，从而缩短神经网络的训练时间，降低各神经元的传输负载。

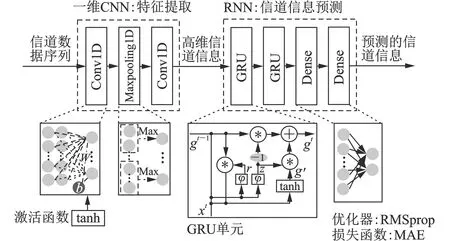
图2 深度神经网络结构

本文构造的预训练网络共有3层。第一层是一维卷积层(Conv1D)，该层通过滑动窗口计算输入数据的卷积和，加权处理后得到该卷积层的输出

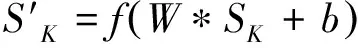
(32)

式中：W表示卷积滤波器，b表示偏移，*表示卷积运算，f(·)表示激活函数。在这个卷积层使用的激活函数为双曲正切激活函数(tanh)，其表达式为

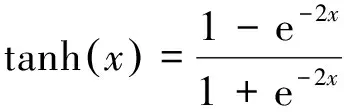
(33)

信道信息经过该卷积层后，原有的信息序列被卷积变换，所有的卷积输出构成一个特征矩阵，并将该矩阵数据输出到网络的下一层。第二层是一维最大池化层(Maxpooling1D)，该层通过池化窗口搜索到上一卷积层输出的最大值，并从特征矩阵中提取特征向量来减少特征参数的数量。此时的信道信息已经被转化成高维的数据表示形式，但其特征被保留了下来。第三层再次堆叠一个一维卷积层，执行与第一层相同的操作，进一步完成特征向量的提取，并准备将预训练后的数据输入到GRU网络中进行信息预测。注意，完成预训练的数据仍然是信道信息，但表达维度更高。

3.2 过时信道信息预测

本文构造的预测网络共有4层。第一层是GRU层，由更新门、重置门和激活函数组成。假设当前GRU层的输入信道信息数据为xt，该层上一次学习后保留的信息gt-1首先经过重置门，将重置后的数据与本次的输入叠加，通过激活函数tanh后，得到的输出g′成功记忆了当前数据，其表达式为

g′=tanh(W·[gt-1*r,xt])

(34)

式中r表示重置门控函数。其表达式为

r=φ(Wr·[gt-1,xt])

(35)

式中：Wr表示重置门滤波器，φ(·)表示Sigmoid函数。然后将该部分输出g′经过更新门，执行信道信息数据的遗忘与记忆过程，表达式为

gt=(1-z)*gt-1+z*g′

(36)

式中z表示更新门控函数。其表达式为

z=φ(Wz·[gt-1,xt])

(37)

式中：Wz表示更新门滤波器。经过该GRU层后，信道信息数据被选择性记忆与遗忘，将过去的记忆保留一部分后与本轮的新知识相加，得到更新后的数据gt。

第二层仍然是一个GRU层，其功能与第一层GRU类似，增强了学习能力，不同之处在于使用的激活函数为线性整流函数(ReLU)，其表达式为

ReLU(x)=max{0,x}

(38)

第三层与第四层是密集层(Dense)，对GRU网络在每个时间步的输出进行加权处理，降低输出维度，最终输出是来自GRU网络的所有数据的加权和，即为预测的信道信息。

所提神经网络的目标是预测准确的信道信息，因此使用的损失函数是平均绝对误差(MAE)函数，该损失函数表示神经网络的预测值与目标值的绝对差值。本文使用RMSprop优化器，降低损失函数值，从而提高预测的准确性。

总的来说，本文设计的深度神经网络，前三层为卷积神经网络，用于预训练信道信息数据；后四层为循环神经网络，用于预测准确的信道信息。所提网络有效地解决了由于CSI反馈延迟导致的通信系统性能下降问题，这一点将在接下来的仿真部分得到验证。

4 数值结果与分析

在本节中，通过理论仿真与蒙特卡罗仿真的数值结果分析系统中断性能，并验证所提神经网络结构在CSI反馈延迟的NOMA网络中的性能。数值结果仿真工具为MATLAB，神经网络编程工具为Python 3.7与Keras。蒙特卡罗仿真为10 000次，为了便于仿真，所有近用户设置在基站与远用户的中点，仿真参数如下：用户服务质量要求Rn=Rd=0.5 bit/s/Hz，Ω1=Ω2=0.064。这里采用离线训练和信道估计，以便于评估如下多种深度学习算法。

仿真结果分为两部分：(1) 将无DL情况下系统中断概率的理论值与蒙特卡洛仿真值对比，将渐近中断概率与准确中断概率进行对比，保证中断概率表达式与分集增益推导的准确，并分析延时相关系数ρ0对中断性能的影响；(2) 基于所提信道信息预测方法，分析近用户数量对中断性能的影响，验证深度神经网络的性能，并将损失函数作为性能指标，比较不同的延时相关系数下各网络结构的学习性能。

4.1 无深度学习的中断性能仿真分析

如图3所示，其中近用户数量N为3个，ρ0=1表示CSI反馈无延迟。蒙特卡罗仿真曲线与理论曲线完全一致，表明所推导的系统中断概率闭式表达式是准确的。在高信噪比时，渐近中断概率曲线与理论曲线相近，且曲线斜率一致，表明分集增益推导准确。对比不同延时相关系数下的理论中断曲线，CSI反馈无延迟时，系统达到全分集，而存在反馈延迟的情况下，无论ρ0值为多少，系统分集增益都降为1，即CSI反馈延迟时多用户系统分集增益消失。此外，延时相关系数越接近1，系统中断概率越小，即反馈延迟越小，系统编码增益越大。

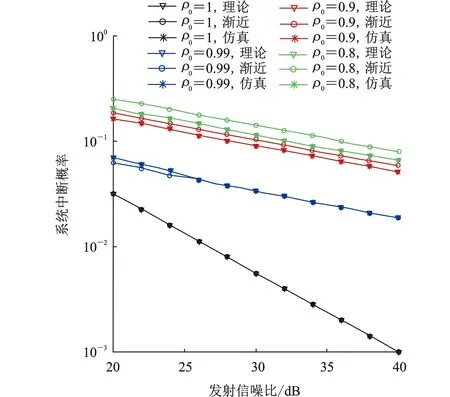
图3 不同延时相关系数的系统中断概率(N=3)

4.2 信道信息预测方法仿真分析

图4仿真了发射信噪比q=20 dB下近用户数量变化时的系统中断概率。随着近用户数量的增多，系统中断概率不断下降。当NOMA网络存在反馈延迟时，系统性能下降严重，近用户数量的增多仅能略微降低系统中断概率。相比之下，基于DL的信道信息预测方法显著提升了系统中断性能，尽管不能完全消除CSI反馈延迟带来的影响，但系统中断概率大幅降低，且近用户越多，性能提升越明显，体现了该预测方法的优越性。

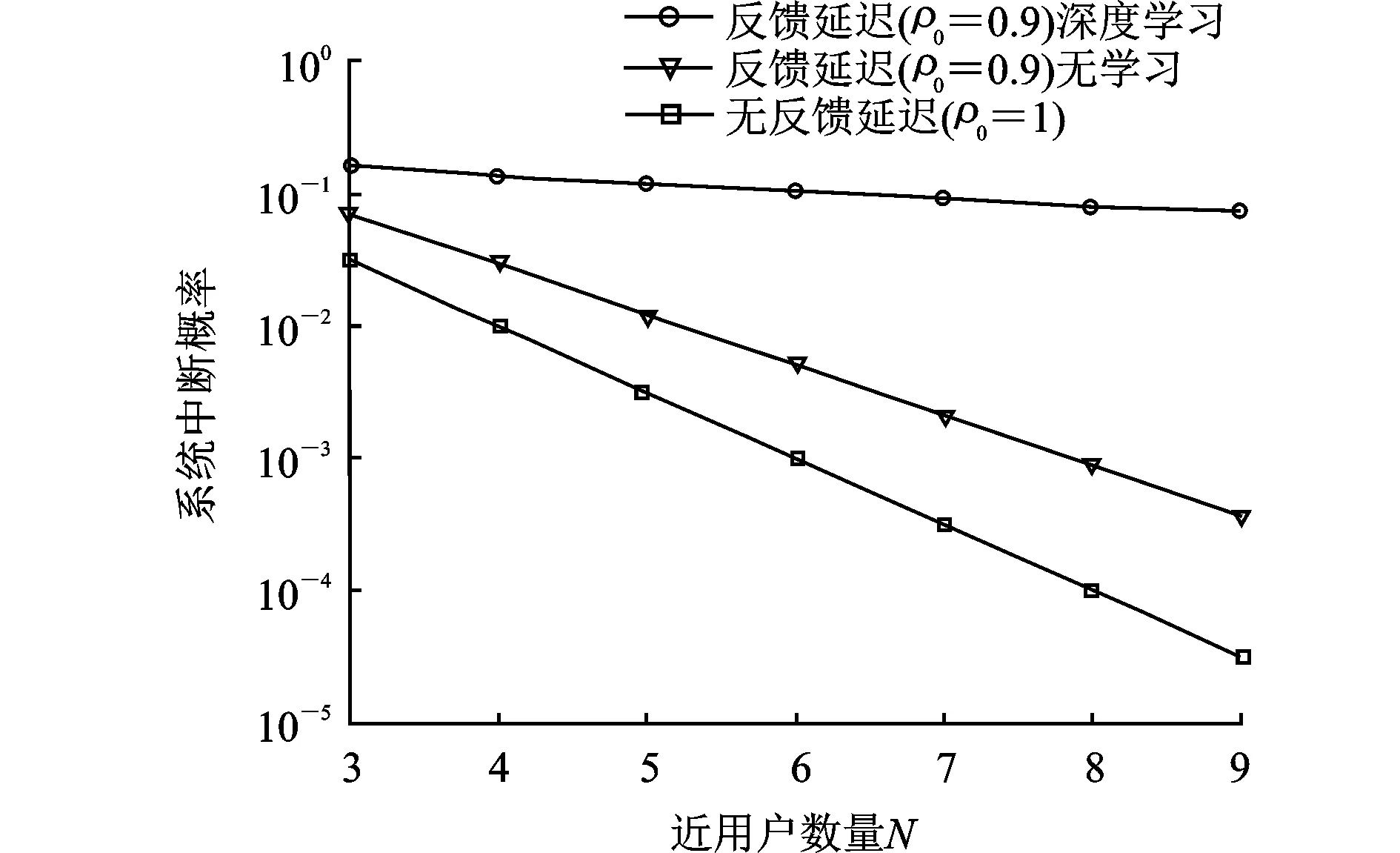
图4 信噪比20 dB下近用户数量对系统中断概率的影响

本文所提预测网络的结构为双层GRU与密集层的叠加，如图5所示。对比其他网络结构，所提预测网络具有更小的平均绝对误差，这表明在本文的CSI反馈延迟问题上，使用GRU网络更合适。此外，从图5中可以观察到，加入Dense层能够增强预测网络的学习性能。值得注意的是，双层GRU网络的收敛速度要略慢于单个GRU层的神经网络，但预测能力更强，这是增强网络学习能力的代价。

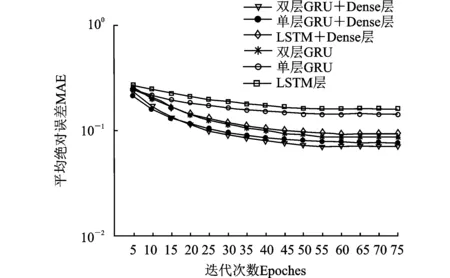
图5 各神经网络结构预测性能

图6仿真了延时相关系数变化对神经网络性能的影响。延时相关系数越大，表示过时CSI与准确CSI的相关性越强，反馈时延较小，神经网络预测的结果更为准确。当延时相关系数为1时，则表示反馈无延迟，网络预测的误差为0。若延时相关系数很小，神经网络最终将无法预测准确的信道信息，相较于相关系数较大时的网络性能，预测误差会扩大至10倍以上，导致无法有效通信。

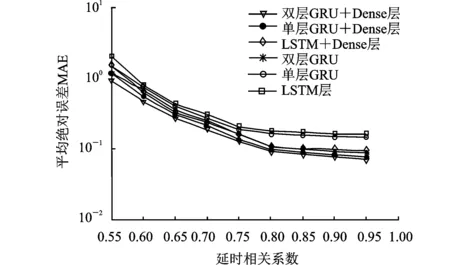
图6 延时相关系数对预测性能的影响

综上所述，过时的CSI会导致系统中断性能下降，NOMA网络中近用户数量越多，CSI反馈延迟的影响越严重，而本文所提信道信息预测方法具有良好的效果，有效预测过时的信道信息并提升了系统中断性能。

5 结论

本文对CSI反馈延迟条件下的用户中继协作NOMA网络进行了研究，根据近用户选择策略推导系统中断概率闭式表达式；分析渐近中断性能，推导系统分集增益。为了更好地选择近用户进行通信，提出基于DL的信道信息预测方法，降低CSI反馈延迟带来的影响，并通过仿真验证了所提方法能有效提升系统中断性能。