以导图启发思维 彰显数学智慧

张镇江

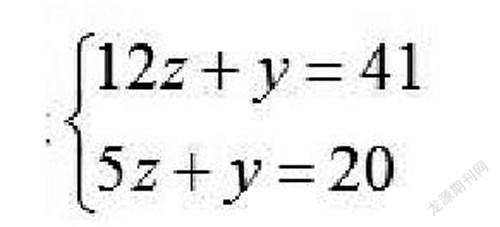
初中学生身心发展规律以及思维水平有了很大进步，为教师继续展开数学教学奠定了基础。然而数学知识本身具有一定的抽象性和逻辑性，需要教师在教学中善于结合学生身心发展规律以及数学知识制定相应教学策略，便于学生高效掌握数学知识点。融入思维导图教学可以化抽象为形象，将数学知识点链接在一起，直观地呈现在学生面前，有利于学生更好地理解相应知识点中的重难点，从而有效完成数学知识框架的构建。

思维导图是一种知识网络结构图。它借助节点和连线来展现知识的网络状态。由于它具备强大的知识工具性，因此在初中数学教学中应用广泛;除此以外，它的存在还适应初中生的身心发展规律以及思维水平特点。一方面，思维导图凭借图像、色彩等强大的视觉功效，将抽象的、不易理解的知识形象化展示，便于学生理解和吸收知识。另一方面，在借助思维导图的学习中，学生可以有意识地尝试构建相关知识的结构框架，对数学的相关概念进行整理和加工，在数学相关问题的探讨中，深入理解数学知识，提高数学思维能力。

一、精准把握数学关键词，构建思维导图框架

在课堂教学中，教师可鼓励学生把握知识中的关键词，之后从数学关键词出发构建完整性数学思维导图。一方面教师以关键词为抓手，以关键词为思考的落脚点，引导学生对数学问题进行思考，在师生互动和生生互动中活跃气氛，强化数学思维。另外一方面教师还应当注重尊重学生之间的差异性，设计思维导图任务，让不同学生结合自我实际能力完成数学思维导图绘制任务，同时鼓励学生之间分享与交流，查漏补缺，促进学生数学思维力的有效提升。

比如七年级第2章第2节《有理数和无理数》教学过程中，为了让学生更好地掌握有理数的分类。根据定义学生抓住关键词：整数和分数。教师通过和学生探讨发现整数可以按照正、负的方式进行分类得：正整数、零和负整数。类比整数的分类方式学生很容易把分数进行分类。在师生探讨的过程中教师利用思维导图的形式将学生得到的结论展示出来，不仅精简地反映了有理数的分类，同时完善了学生对有理数的认识，之后让学生通过已有的分类进行思考，怎样对有理数再分类？学生通过观察发现整数和分数都可以按照正、负进行分类，从而利用类比的方法对有理数进行了再分类，通过对正、负有理数的深入认识，将正有理数和负有理数划分不同种类，最终构建属于自己的数学思维框架图，具体如下

学生绘制完成有理数分类思维导图任务之后，发现忽略了无理数，之后对于无理数进行探究，教师给学生以提示，是不是所有的数都是有理数呢？正当学生愁眉不展的时候，教师将两个小正方形对折剪开，之后重新拼接成为一个大正方形，剪开的边当作大正方形的边长，其面积为“2”，大正方形的边长为e，而e是无限不循环的小数，不能写成分数形式，教师顺利引出无理数的概念，让学生共同回归课本，寻找其他的无理数，比如小学时就学过的圆周率也是无理数。学生在数学知识学习中完成数学思维导图构建任务，同时从数学关键词有理数和无理数出发，进行分类与汇总，形成属于自己的数学思维框架图，为学生后续解决数学实际问题做好铺垫。

二、汇总思维导图知识，化抽象知识为形象知识

初中阶段数学教师教学任务逐步从数学知识传授转变为学生逻辑思维力的培养。传统教学方式直接为学生讲述数学知识，会导致学生对于数学知识理解停留在机械式记忆中，无法运用所学习知识解决实际问题。融入思维导图教学则恰好解决了当前所存在的困难，教师将部分数学知识点汇总到思维导图中，让学生对于抽象数学知识形成直观性的認知，深化学生数学理解，为学生后续解决实质性问题奠定基础。

例如在课堂教学中讲授七上第4章第2节《解一元一次方程》相关知识点时，教师为学生展现方程式（1）2x+1=5，（2）3x-2=4x-3，让学生分别将“0/1/2/3/4”代入到方程中，发现x=2，x=1，分别使得两个等式成立，从而引出方程的解的概念。如何求解方程的解？接下来教师展示天平，利用天平表示2x+1=5的方程，结合天平的特点，组织学生将方程两边同时减去“1”，使得方程变成2x=4，再利用天平的特点，将两边同时除以“2”，最终获得的x=2答案。当学生完成解方程的过程之后，教师提出问题，能否借助天平的特性来解释方程的求解呢？我们可以将方程看成天平，方程两边的式子同时进行加减相同的数或整式，方程的解不变，这相当于天平的两边同时加减相同质量的砝码，天平仍然保持平衡。同样的天平的两边砝码的质量扩大或缩小相同的倍数，天平仍能保持平衡，对应于方程的求解，容易推导出等式的基本性质即等式两边同时乘上或者除去一个数（除0以外），其结果是等式依然成立。最后环节中教师引领学生将所学习数学知识进行思维导图绘制，形成直观性数学认知，具体思维导图展示如下：

学生汇总思维导图知识，将解一元一次方程的过程生动呈现了出来，无论两边公式如何变化，只要保持同步变化，那么公式就始终保持平衡，将解一元一次方程的抽象过程转变为直观形象的知识，深化了学生对数学知识的认知。

三、绘制简单有效的思维导图，实现从特殊到一般的学习

应用思维导图教学时，应当让学生认识到数学知识之间本身存在一定的联系性，面对同类型的数学问题则采取同类型的数学方法，引领学生对于数学方法进行归类与总结，引领学生在数学学习中通过自主创新求得新知识的解决方法。同时教师在教学新知识的过程中，要善于连接旧知识，深化学生对于数学知识的感知，实现从特殊到一般的过渡，激发学生对于数学知识的探究欲望。

例如在七上第七章《多边形的内角和与外角和》的教学中，为了解决多边形的内角和知识的求解，教师提前用卡纸做三角形、四边形、五边形……在学生学习了多边形的定义和多边形的对角线知识之后，展示教具，学生分组讨论如何求多边形的内角和。通过反馈发现可以利用连接对角线，将多边形分割成三角形，借助三角形的内角和求多边形的内角和。从多边形的一个顶点画对角线，发现四边形可以分割成两个三角形，由三角形的内角和180°易得四边形的的内角和为360°。之后使用相同的方法继续探索，发现五边形可以分割成三个三角形，六边形可以分割成四个三角形……由此可知五边形的内角和180°×3=540°。六边形的内角和180°×4=720°。展示所得结果并让学生思考六边形、七边形……的内角和如何求解？带领学生总结多边形内角求和的规律，得到n边形内角和公式为180°（n-2）。最后将学习的多边形内角和探究环节绘制成为思维导图，从思维导图视角出发，整合多边形内角和知识，实现从特殊到一般的过渡，通过思维导图，帮助学生更好地解决了多边形内角和的求解问题。

四、运用思维导图解析问题，由浅入深完成学习任务

对学生数学思维的培养已成为当前数学课堂教学中的重要课题。数学思维的建立有助于学生形成完整性数学思维框架。当学生构建了完整性数学思维框架之后，才能够灵活性运用所学的数学知识解决问题，促进学生数学思维力的提升。初中阶段数学知识则是从烦到简，层层递进，教师教学中重点关注数学知识难易程度，注重有层次地将数学知识展现出来，让学生从数学知识学习中形成数学学习兴趣，深化对于所学习知识的渗透，感知数学概念以及数学定理的内涵，在层层递进中完成数学学习任务。

比如在七下第10章第4节《三元一次方程组》的教学中，要求学生会解简单的三元一次方程组。并在解析中体会消元数学思想。首先创设教学情境“我校篮球队参加区篮球赛，比赛规则：胜一场3分，平一场1分，负一场0分，我校篮球队经过激烈的比赛，最终比赛22场，共得47分。比赛中获胜的场数是负的场数的4倍多2场。求我校球队的比赛情况”，通过分析发现有三个未知量，且找到了三个等量关系。设胜x场，平y场，负z场，可得

通过探究得出一个三元一次方程组，让学生进行小组讨论可知使用代入法可消去其中一个未知数而得到一个二元一次方程

然后通过加减得到7z=21，根据z=3代入方程组得方程组的解

通过对三元一次方程组的求解，学生发现解题的关键还是消元。和二元一次方程组一样，使用加减法或代入法，将三元的方程组转变成二元方程组再转化为一元一次方程。最终求得答案。引领学生在层层递进中完成三元一次方程组的学习任务，习得初步运算技能。

综上所述，思维导图的使用，不仅可以形象地加深学生对相关知识点的认识，而且可以锻炼学生的逻辑思维能力，同时还能提高学生的数学理解和运算能力，巩固数学知识学习效果，促使学生在深度掌握数学知识基础上获得更多能力的发展。当然，作为一种有效教学工具，运用思维导图教学还需要教师在实践中不断加以研究、完善，使其发挥出最大功效。