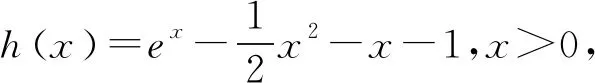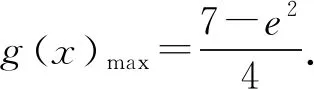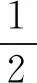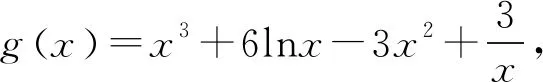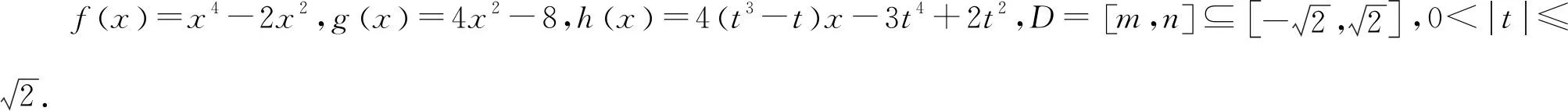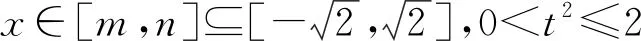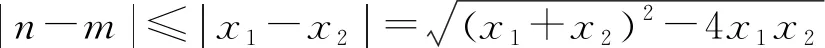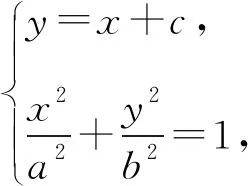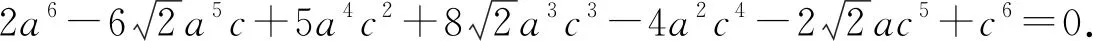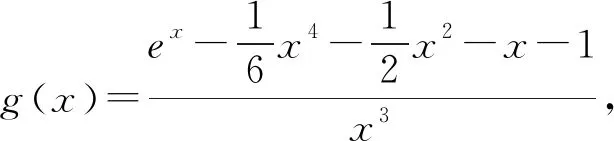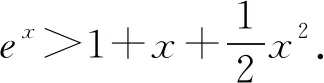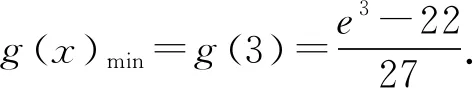妙用多项式除法求解导数与解几压轴试题

苏艺伟 陈艺平

(福建省龙海第一中学新校区 363100)

多项式除法定理设f(x),g(x)是两个多项式,且g(x)≠0,则恰有两多项式q(x)及r(x)使得f(x)=q(x)g(x)+r(x)成立,其中r(x)=0或degr(x)

通俗地说,多项式除法是代数中的一种运算,用一个多项式去除以另一个多项式,从而将一个相对复杂的除法问题分解成更小的一些问题.借助多项式除法定理可以解决导数与解几压轴试题中一些较难的多项式分解问题,从而突破难点,化繁为简,化抽象为具体,实现解题的高效.

例1(2020年全国Ⅰ卷理科第21题)已知函数f(x)=ex+ax2-x.

(1)当a=1时,讨论f(x)的单调性(略).

当x=0时,a∈R.

只需a≥g(x)max.

则h′(x)=ex-x-1,

h″(x)=ex-1≥0,

所以h′(x)在(0,+∞)上单调递增.

所以h′(x)>h′(0)=0.

故h(x)在(0,+∞)上单调递增.

所以h(x)>h(0)=0.

令g′(x)=0,得x=2.

所以g(x)在(0,2)上单调递增,在(2,+∞)上单调递减.

所以g(x)在(0,1)上单调递减,在(1，+∞)上单调递增.

所以g(x)有极小值g(1)=1,无极大值.

简析对于多项式x4-2x3+2x-1,经检验可知x=-1是方程x4-2x3+2x-1=0的一个实根,借助多项式除法得到另外一个因式x3-3x2+3x-1.通过验根和多项式除法,顺利将g′(x)进行化简,从而突破难点.

证明由已知可得

①

②

先考虑第①个不等式,转化成

(x-t)2(x2+2tx+3t2-2)≥0.

Δ=8(1-t2).

若00,则

若1≤t2≤2,Δ≤0,此时考虑不等式②.

设4x2-4(t3-t)x+3t4-2t2-8=0的两个实根为x1,x2,

令t2=λ,则λ∈[1,2].

记f(λ)=λ3-5λ2+3λ+8,则f′(λ)<0,故f(λ)的最小值为7.

简析对于方程x4-2x2-4(t3-t)x+3t4-2t2=0，经检验可知x=t是一个实根,借助多项式除法得到另外一个因式x3+tx2+t2x-2x-3t3+2t.

经检验可知x=t是x3+tx2+t2x-2x-3t3+2t=0的一个实根,再次用多项式除法得到另外一个因式x2+2tx+3t2-2.因此将不等式(1)转化成(x-t)2(x2+2tx+3t2-2)≥0,从而突破难点.

例4 已知直线x-2y-1=0与抛物线y2=4x交于A,B两点,C为抛物线上的一点,∠ACB=90°,求点C的坐标.

y2-8y-4=0.

设A(x1,y1),B(x2,y2),C(t2,2t),AB中点为D,

则y1+y2=8,y1y2=-4.

故AB=x1+x2+p=2y1+1+2y2+1+2=20,CD=10,D(9，4).

令(t2-9)2+(2t-4)2=100,得

t4-14t2-16t-3=0.

③

经检验,t=-1是方程③的一个实根.

所以t4-14t2-16t-3含一个因式t+1.

进一步,用t4+0·t3-14t2-16t-3除以(t+1),得到t3-t2-13t-3.

经检验,t=-3是t3-t2-13t-3=0的一个实根,所以t3-t2-13t-3含一个因式t+3.

进一步,用t3-t2-13t-3除以(t+3),得到

t2-4t-1.

因此,方程③可以转化成

(t+1)(t+3)(t2-4t-1)=0.

由于点C(t2,2t)不在直线x-2y-1=0上,

所以t2-4t-1≠0.

故C(1，-2)或C(9，-6).

简析对于方程t4-14t2-16t-3=0,发现有一个实根t=-1,借助多项式除法得到另外一个因式t3-t2-13t-3,进一步发现t=-3是t3-t2-13t-3=0的一个实根,再次运用多项式除法,得到t2-4t-1.故而最终分解成(t+1)(t+3)(t2-4t-1)=0.

解析联立直线和椭圆方程求出点A坐标,然后代入抛物线方程.

(b2+a2)x2+2a2cx+a2c2-a2b2=0.

所以Δ=8a2(a2-c2)2.

由求根公式有

将点A坐标代入抛物线方程y2=4cx,得

化简,得

两边同时除以a6,得

④

⑤

⑥

两边再同时除以e2,得

⑦

解析由已知可得

故2c4+2c3a=12a4+12a3c+3a2c2.

即2e4+2e3-3e2-12e-12=0.

即(e-2)(2e3+6e2+9e+6)=0.

故e=2.

简析观察到方程2e4+2e3-3e2-12e-12=0,有一个实根e=2,借助多项式除法得到另外一个因式2e3+6e2+9e+6,从而求出离心率.

解析设直线AM方程为y=kx+b,

代入b2x2+9y2=9b2，

得(9k2+b2)x2+18kbx=0.

令|AM|=|AN|,得

设k>0且k≠1,则

b2k3-9k2+9k-b2=0.

即(k-1)[b2k2+(b2-9)k+b2]=0.

方程b2k2+(b2-9)k+b2=0有大于0且不等于1的正实根.

故Δ≥0且b2+b2-9+b2≠0,0

简析观察到方程b2k3-9k2+9k-b2=0,有一个实根k=1,借助多项式除法得到另外一个因式b2k2+(b2-9)k+b2,从而求出实数b的取值范围.

不难发现,对于此类导数与解几压轴试题中的多项式化简问题,在难以直接因式分解的前提下,可以采用先验根,得到一个因式,再借助多项式除法得到另外一个因式,从而将多项式分解成若干项之积,将复杂的问题转化成简单的问题,提高学生的数学运算能力,培育数学运算素养,可谓大道至简,柳暗花明又一村.

解析由已知,得

只需a≤g(x)min.

又当x>0时,ex>x+1,

故令g′(x)=0,得x=3.

故g(x)在(0,3)单调递减,在(3,+∞)单调递增.