热电材料Ca3Co4O9掺杂Ag、Yb改性的量子化学计算

王成江，张 婧，祝梦雅，曾洪平

(三峡大学电气与新能源学院，湖北宜昌 443002)

近年来碳排放量加速攀升对生态系统造成了严重威胁，超过半数的能源能量以废热形式散失。因此发展低碳经济、重塑能源体系至关重要。政府明确要求扎实做好碳达峰、碳中和各项工作，优化产业结构和能源结构。在此背景下，可以将低品位热能直接转换成电能的温差发电技术成为众多研究者关注的焦点[1]。温差发电技术依靠热电材料的热电转换效应实现。氧化物热电材料矢配型钴酸盐Ca3Co4O9凭借其在高温条件下的稳定性更高、抗氧化性更强、成本更低、对环境友好等显著优点，在利用工业废热发电等高温领域具有良好的发展前景[2]。

但低功率因子使Ca3Co4O9应用受限，目前已有学者利用实验手段对提升Ca3Co4O9性能进行了研究。经实验验证，在Ca3Co4O9的Ca 位掺杂异原子已被证实可改进其热电性能[3]。研究表明Ag 作为金属元素取代Ca 后有利于Ca3Co4O9电导率的提升，Yb 作为稀土元素取代Ca 后更有利于塞贝克系数的提升[4]，但效果不够理想，且实验方法只能从宏观结果进行讨论，不能揭示性能提升的微观机理，更无法在原子层面解释性能提升的原因。分子模拟技术可模拟实验方法尚无法考察的现象和过程，从微观角度为热电材料的研发、性能提升提供理论支撑[5]。基于量子化学密度泛函理论的分子模拟可在微观层面上描述掺杂过程，分析掺杂对材料性能的影响。

考虑到Ag 和Yb 的单掺杂改进Ca3Co4O9性能的机理不同，本文对比Ca 位单掺杂Ag、Yb 体系与Ca 位双掺杂Ag-Yb体系，在微观层面探究双掺杂Ag-Yb 改进Ca3Co4O9性能的可能性。

1 热电性能的微观表征

1.1 功率因子

热电材料的性能取决于其功率因子PF，PF值越高，性能越好。而塞贝克系数S和电阻率ρ 是影响功率因子PF的指标，其关系为：

1.2 马利肯键布居

材料的性质与化学键强度关系紧密，马利肯以波函数分析，采用键布居来判断成键特性与化学键强度[6]。马利肯键布居数表示原子间键级的强度，该值越大，意味着原子间键级越强。根据Slack[7]提出的理想热电材料理论，弱结合的化学键是使得材料电阻率低的原因之一。

1.3 态密度

态密度可体现材料内部载流子分布与运动规律，能显示各轨道内的电子分布情况，揭示电子输运性质，表征电导率。总态密度按照相关规则分配到各原子上被称为分态密度，表示单个原子对能带的贡献。分析态密度和分态密度可解释掺杂前后材料性能变化。

根据态密度还可分析赝能隙特性。赝能隙为费米能级两侧两个尖峰的宽度，可直接反映体系化学键的强弱，赝能隙越宽，原子间成键越强，进而表征材料的电阻率。

1.4 载流子相对质量

热电材料通过内部载流子运动来实现电、热能之间的直接转换，其本质为载流子输运作用。有效质量概念的引入给讨论载流子运动带来了方便。

由固体物理的知识可知有效质量m0的表达式：

式中：h为普朗克常数；E(k)为极值处的能量。m0与电子质量me(me=9.1×10-31kg)的比值定义为载流子相对质量m1，即：

西南大学刘静等[8]推导塞贝克系数与载流子相对质量正相关，故m1可表征材料热电性能。

2 仿真建模及计算

Ca3Co4O9是由拥有等同的a、c、β 参数和不同的b参数的两个子系统[Ca2CoO3]层和[CoO2]层沿c轴相互交替堆叠而成的结构[3]。b轴方向两层晶胞的比例不一致为建立Ca3Co4O9计算模型带来了困难。为使计算更加可行，取b轴比例为b1/b2=1.5，结构表达式为[Ca2CoO3][CoO2]1.5。图1 为Ca3Co4O9的计算理论模型，模型中共有42 个原子，即Ca8Co10O24。考虑理论模型与实际的接近程度，单掺杂Ag、Yb 的掺杂比例取0、0.062 5、0.125 0、0.250 0、0.375 0，即分别取代Ca8Co10O24理论模型中的0.5、1、2、3 个Ca 原子；图1(b,c)是单掺杂比例Ag、Yb 为0.125 的模型图；图1(d)是双掺杂比例Ag 和Yb 分别为0.125 的模型图。本文计算使用基于密度泛函理论的Materials Studio 软件包中的CASTEP 模块完成，分别对Ca8Co10O24、(Ca1-xMx)8Co10O24(M=Ag、Yb，x=0.062 5、0.125 0、0.250 0、0.375 0)以及(Ca1-x-yAgxYby)8Co10O24体系进行量子化学计算，计算前对模型进行相同的几何优化。

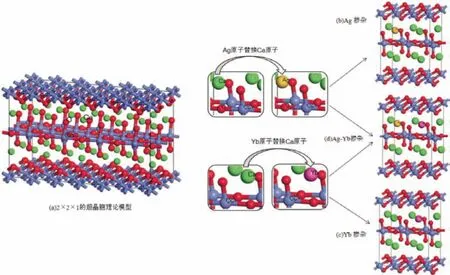
图1 Ca8Co10O24及掺杂体系的晶体模型结构图

3 单掺杂Ag、Yb 的Ca8Co10O24体系计算结果与讨论

3.1 马利肯键布居分析

根据原子排布列出模型中心原子单掺杂Ag、Yb前后原子之间的键布居数如表1、表2所示，表内各值取平均值。分析可得：Ag 掺杂比例x=0.062 5 时，Ca2CoO3层中的Ag-O1、Co1-O2、Co1-O3较掺杂前均减小；x=0.125 时，Ca2CoO3层中的Ag-O1、Co1-O2、Co1-O3以及CoO2层中的Co3-O4、Co2-O5较掺杂前均减小；但随着Ag 掺杂比例继续增加，除Ca2CoO3层的Co1-O2键略有减小外，大部分原子之间的键布居数呈增大趋势。

表2 (Ca1-xYbx)8Co10O24 的马利肯键布居(平均值)

Ca8Co10O24模型体系中共有4 个Ca1-O1、Ca2-O1、Co1-O1、Co1-O2、Co1-O3及6 个Co3-O4、Co2-O5。根据表1 计算出体系马利肯总键布居数为8.674。随着Ag 掺杂比例增大，体系化学键总数未改变，马利肯总键布居数随掺杂比例变化趋势如图2 所示，表现为先减弱后增强。当x=0.125 时，马利肯总键布居数最低，相较于未掺杂体系下降了2.6%，该比例下体系的化学键强度最低，可更大程度改善材料性能。Zhang 等[9]采用溶胶凝胶法制备了Ca3-xAgxCo4O9(x=0.1～0.6)，当x=0.3，即掺杂比例为0.1 时，样品的功率因子提高了70%，与本文分析结果相近。

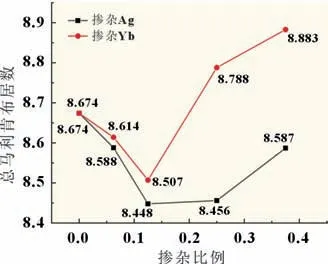
图2 单掺杂体系马利肯总键布居变化

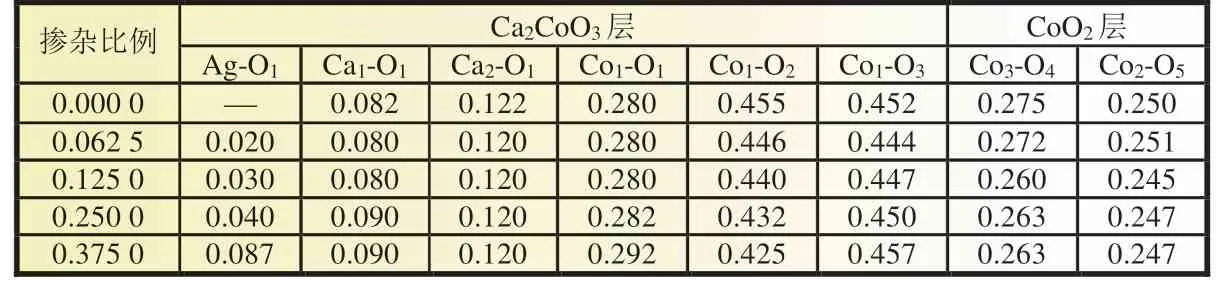
表1 (Ca1-xAgx)8Co10O24 的马利肯键布居(平均值)

Yb 掺杂比例x=0.062 5 时，Ca2CoO3层中的Yb-O1、Ca1-O1、Ca2-O1、Co1-O2键与Co1-O3键比掺杂前低；x=0.125 时，Ca2CoO3层中的Yb-O1、Co1-O2、Co1-O3以及CoO2层中的Co3-O4、Co2-O5较掺杂前进一步减小；Yb 掺杂比例继续增加后，除Co1-O2键减小外，其余键级均呈增大趋势。

由图2 分析得，随着Yb 的掺杂比例增加，马利肯总键布居数变化趋势为先减弱后增强，当x=0.125 时，马利肯总键布居数最低，相较于未掺杂时下降了1.9%，但随着掺杂比例的提升，马利肯总键布居数比未掺杂时增强，相应体系的电阻率比未掺杂时增加。由此可知，Yb 元素的掺杂比例不宜过大，否则会抑制材料性能的提升。褚颖等[10]采用溶胶凝胶法合成了Ca3-xYbxCo4O9(x=0,0.15,0.30,0.45)，其中当x=0.30，即掺杂比例为0.1 时，材料的功率因子最佳，与本文计算的最优比例相近。

3.2 态密度分析

图3(a～c)为Ca8Co10O24、Ca7AgCo10O24、Ca7YbCo10O24模 型的总态密度图和成键原子的分态密度图，费米能级位于虚线处，态密度峰值和赝能隙宽度计算结果如图所示。就Ca8Co10O24模型来说，其导带范围在0～16 eV。在Ca2CoO3层中，Ca1在费米能级附近的分态密度值几乎为0，Co1s 对价带和导带的贡献较小，而Co1d 在费米能级右侧分态密度出现峰值，对导带的贡献较大，O1p 在费米能级左侧分态密度出现峰值，对价带的贡献较大。在CoO2层中，Co2s 对价带和导带做的贡献较小；Co2d 贡献较大，O4p 轨道对-4 eV 以外价带有贡献，O4p 轨道峰值距费米能级较近，对导带贡献较大。故Ca8Co10O24的总态密度中费米能级附近的价带和导带主要由Co d 和O p 轨道贡献。

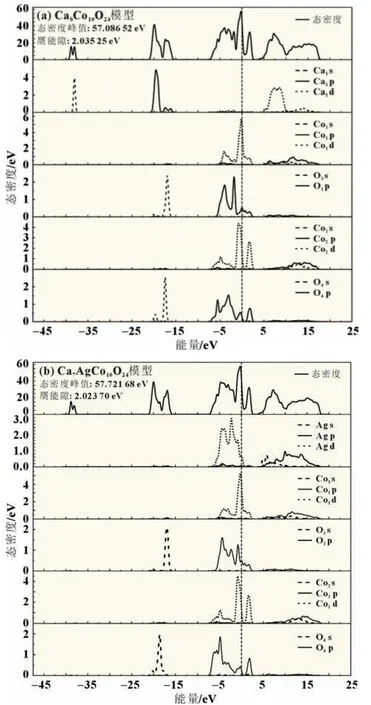
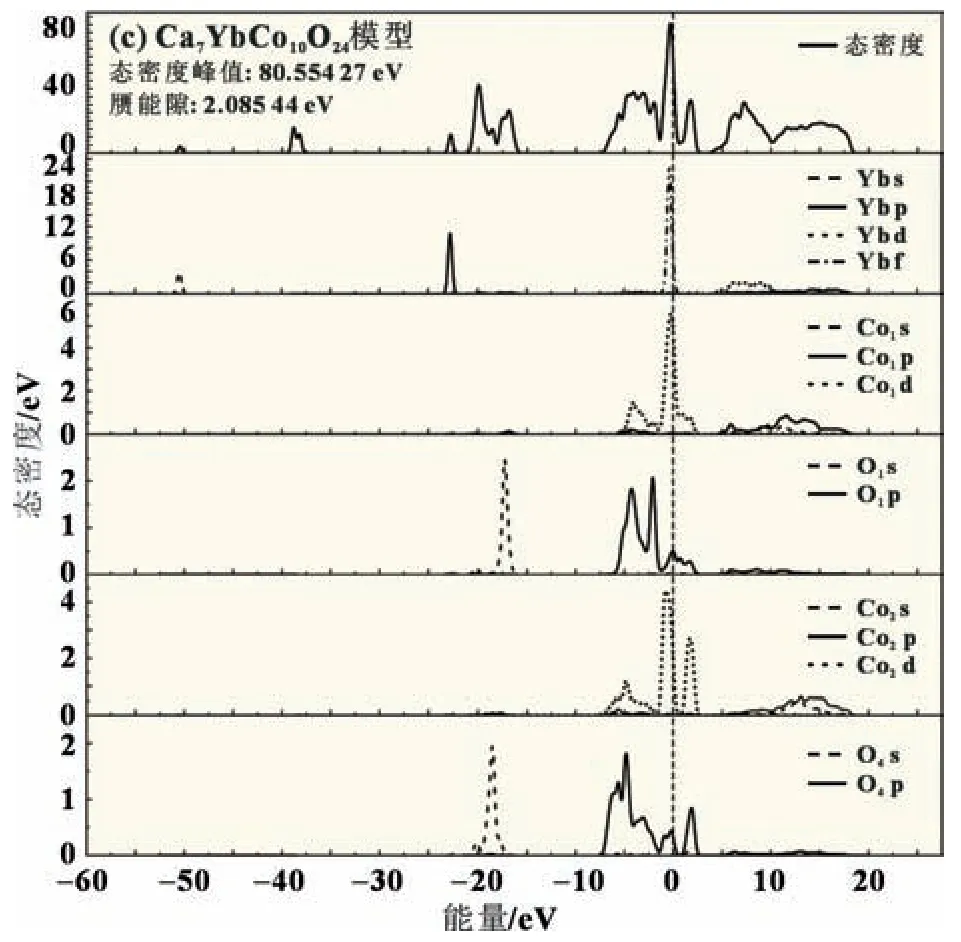
图3 Ca8Co10O24、Ca7AgCo10O24、Ca7YbCo10O24模型的总态密度图和分态密度图

与Ca8Co10O24相比，Ag d 轨道与掺杂前Ca1各个轨道相比在费米能级附近出现明显起伏，分态密度值增加，说明掺杂Ag 后材料可容纳的载流子数增加，更有利于载流子跃迁，提升导电能力；Ag p 轨道的主峰明显比Ca8Co10O24中的Ca1p 分态密度主峰靠近费米能级，Ag p 对价带的贡献比Ca 更大。对比掺杂前后体系的赝能隙发现，Ag p 轨道与Co、O 轨道杂化后，将会导致体系赝能隙宽度下降，体系化学键强度减弱，材料的导电性将提高。

与Ca8Co10O24相比，Yb 取代Ca 后的模型总态密度在费米能级附近的主峰值比未掺杂时增大了22.8 eV，价带顶部明显上移。这是因为Yb 取代Ca1 后在费米能级处多出一条f 轨道，是由Yb 原子贡献的。价带顶部态密度被Yb f 取代，与Co、O 轨道杂化后，价带顶部会上移，这会导致带隙减小，使载流子更容易从价带跃迁至导带，从而有利于材料的电阻率降低，导电性增强。

3.3 载流子相对质量

当掺杂比例x取0.125 时，Ca7AgCo10O24与Ca7YbCo10O24相对于其他掺杂比例体系的性能更加理想，根据式(2)和(3)计算得Ca8Co10O24、Ca7AgCo10O24与Ca7YbCo10O24的载流 子相对质量m1如表3 所示。

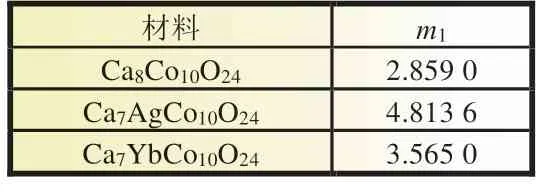
表3 载流子相对质量m1

可以看出，Ca7AgCo10O24与Ca6YbCo10O24的m1明显比Ca8Co10O24大，分别提升了1.68 倍、1.25 倍。塞贝克系数与m1正相关，m1的提升有利于材料塞贝克系数的提高，促进功率因子提升。Zhang 等[9]制备的Ca2.7Ag0.3Co4O9也具有比本征材料更高的塞贝克系数。

4 双掺杂Ag-Yb 的Ca8Co10O24 体系的计算结果与讨论

材料的性质依赖于其电子结构，分析量子化学计算结果，可以帮助人们厘清材料性能提升的相关机制，进而为改性新材料提供合适方案。通过上节分析得，单掺杂Ag、Yb 有利于提升热电材料性能，当掺杂比例x=0.125 时提升效果最佳，基于此比例，本节建立了Ca 位双掺杂Ag-Yb 的Ca8Co10O24模型，双掺杂比例分别取0.25-0.125、0.125-0.125、0.125-0.25，对应模型为Ca5Ag2YbCo10O24、Ca6AgYbCo10O24和Ca5AgYb2Co10O24，探究双掺杂异元素Ag-Yb对于材料性能的影响。

4.1 马利肯键布居分析

表4 为Ca5Ag2YbCo10O24、Ca6AgYbCo10O24以及Ca5AgYb2-Co10O24体系的马利肯键布居数。双掺杂两种不同种类元素的情况下，Ag-O1键布居数小于Ca8Co10O24中相对应的Ca-O1，Yb-O1键布居数小于单掺杂体系中相对应的键，其余键的布居数与未掺杂及单掺杂体系中相对应的键相比均减小。

根据表4 计算得，三个体系总键布居数分别为8.188、8.256、8.226，体系整体键布居数均小于单掺杂体系，与未掺杂时相比，双掺杂体系键布居数最低下降5.6%，体系整体化学键键级进一步降低，证明双掺杂Ag-Yb 为提升本征材料性能的手段之一。

表4 双掺杂体系的马利肯键布居(平均值)

4.2 态密度分析

本节分析了Ag-Yb 双掺杂模型的总态密度和分态密度。从图4 可分析得：双掺杂体系的导带范围为0～16 eV 之间，主要由Yb d、Ag s、Ag p、Co1p、O1p、Co2d、O4p 提供，且由于Yb f、Ag s 以及Co d、O p 共同杂化，费米能级处总态密度峰值进一步增大，价带顶部上移，相对于单掺杂上移程度更大，材料的导电性将增强。双掺杂体系求得的赝能隙均小于未掺杂和单掺杂时的体系，表明双掺杂使得体系化学键强度更低，同样有利于材料功率因子提升。

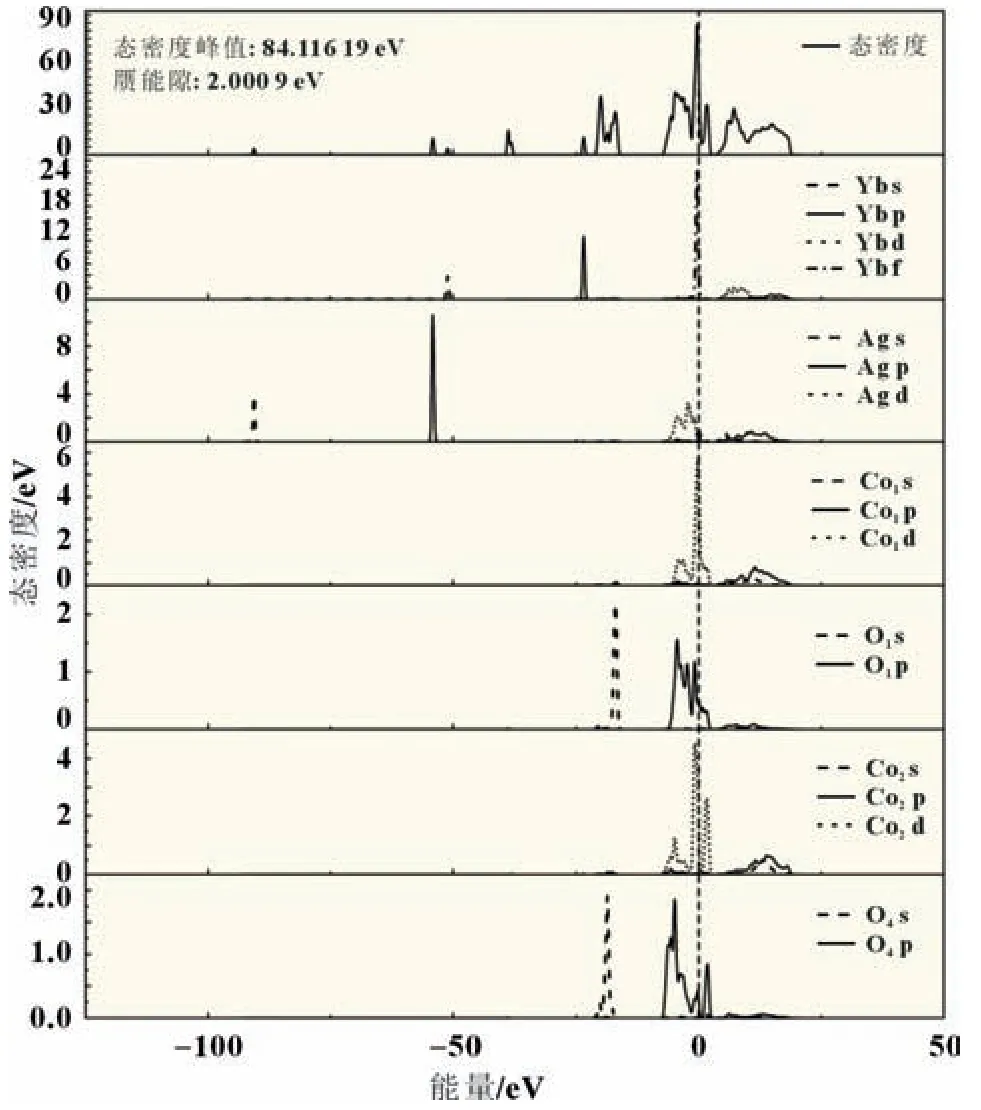
图4 Ag-Yb双掺杂模型的总态密度和分态密度

4.3 载流子相对质量

根据式(2)、(3)计算得Ca5Ag2YbCo10O24、Ca6AgYbCo10O24与Ca5AgYb2Co10O24的载流子相对质量m1如表5 所示。

表5 载流子相对质量m1

可以看出，双掺杂体系m1相比于未掺杂时分别提升2.27倍、1.75 倍、2.03 倍，提升幅度均大于单掺杂体系,说明双掺杂Ag-Yb 比单掺杂更有利于材料塞贝克系数的提高。

由上述分析得，Ag-Yb 双掺杂对于热电材料性能的改善明显优于Ag、Yb 单掺杂，其中Ca5Ag2YbCo10O24的马利肯键布居数、载流子相对质量以及态密度的变化较其他两个模型而言更为理想,即热电材料Ca3Co4O9双掺杂Ag-Yb 为2∶1 的比例时效果更好。

5 结论

本文基于量子化学密度泛函理论计算Ca3Co4O9掺杂Ag、Yb 后微观热电性能指标的变化，结论如下：

(1)随着Ca 位单掺杂Ag、Yb 比例增加，键布居数呈先减弱后增强趋势。当掺杂比例x为0.125 时，Ag、Yb 单掺杂体系总重叠布居数最低。双掺杂Ag-Yb 体系的键布居数将进一步降低，更利于降低材料电阻率；

(2)掺杂Ag 后体系赝能隙减小，化学键强度降低。掺杂Yb 后费米能级处态密度值显著增加，价带顶部上移，带隙减小。而双掺杂Ag-Yb 效果比单掺杂时更明显；

(3)掺杂后的载流子相对质量与Ca8Co10O24比均有提升，双掺杂Ag-Yb 体系提升幅度更大，最大为未掺杂时的2.27倍，有利于材料塞贝克系数的改善。

结果表明，Ca 位双掺杂Ag-Yb 比单掺杂能明显提升Ca3Co4O9性能，Ag-Yb 掺杂比例为2∶1 时更为理想。证明了双掺杂金属元素和稀土元素进一步提升热电材料性能的可行性，为探索新型热电材料提供思路。