蓄电池与超级电容混合储能系统协调控制策略

王 佳，文小玲，罗心睿

(1.武汉工程大学电气信息学院，湖北武汉 430205；2.武汉纺织大学电子与电气工程学院，湖北武汉 430205)

目前，由蓄电池和超级电容构成的混合储能系统被广泛引入直流微电网中，用于抑制分布式电源和负载带来的功率波动[1]。然后，存在以下问题：(1)超级电容具有功率密度大和能量密度低的特点，当系统功率频繁波动时，如果不及时恢复其荷电状态(SOC)、会出现过充或过放现象，从而不仅无法解决系统的功率波动问题、而且会减少其使用寿命；(2)通常采用下垂控制方法来解决直流微电网中混合储能系统的功率分配问题，但因传统下垂控制的固有特性而存在母线电压偏差的缺陷[2]；(3)混合储能瞬时功率分配和超级电容SOC恢复之间存在矛盾。因此，本文提出一种混合储能系统协调控制策略，即通过下垂控制实现系统功率分配，通过直流母线电压补偿控制来恢复母线电压并可以同时恢复超级电容的SOC，最后通过系统参数设计来实现混合储能瞬时功率分配与超级电容SOC恢复的解耦。

1 混合储能系统功率分配策略

在微电网中，广泛采用下垂控制方法解决蓄电池和超级电容的功率分配问题。根据传统下垂控制方法可得等效电路图，见图1。

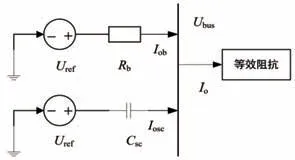
图1 混合储能系统的等效电路

由图1 可得下垂控制的表达式为[3]：

式中：Uref为直流母线电压的额定值，即母线电压参考值；Uob和Iob为蓄电池充放电变换器的输出电压和电流；Uosc和Iosc为超级电容充放电变换器的输出电压和电流；Csc为虚拟电容；Rb为下垂电阻，其大小由母线电压最大允许偏差ΔUmax和变换器输出电流的额定值Iobmax之比。

若不考虑变换器输出端线路阻抗，则有Uob=Uosc=Ubus，从而得到蓄电池、超级电容充放电变换器的输出电流：

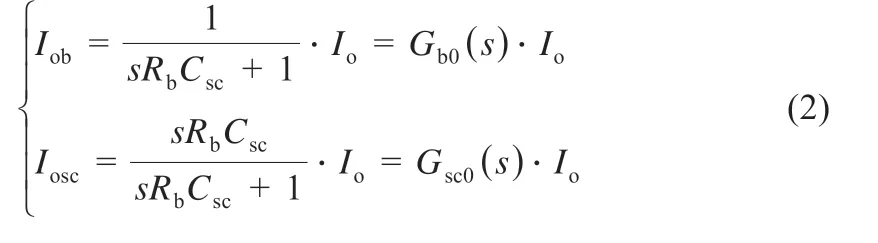
式中：Gb0(s)和Gsc0(s)分别为一阶低通滤波器和一阶高通滤波器的标准形式，通过Gb0(s)和Gsc0(s)可以将负载电流自动分为给超级电容的高频和给蓄电池的低频分量。但是下垂控制会导致直流母线电压下降，因此要进行直流母线电压补偿控制。

2 采用母线电压补偿的超级电容SOC 自主恢复控制策略

采用传统下垂控制，会因虚拟电阻产生的压降而导致直流母线电压值与额定值存在偏差，影响微电网中负载和其他设备的正常运行。为此提出一种直流母线电压补偿策略，其控制框图如图2 所示。

图2 直流母线电压补偿控制原理图

由式(1)可知，由于虚拟电容隔直通交特性，系统稳态时超级电容储能变换器输出电流为零，线路阻抗压降为零，因此超级电容器储能变换器输出电压Uosc与直流母线电压Ubus相同。若要获得直流母线电压，只需要获得Uosc。该补偿控制策略通过PI 控制器实时调控补偿电压值，实现母线电压稳定在额定值。

系统没有母线电压补偿时，两台变换器的输出电压控制方程为式(1)，采用母线电压补偿控制后，母线电压满足：

采用所提的控制方法，比例积分控制器产生的补偿电压ΔUref等效为在蓄电池变换器输出端串联一个虚拟电压源，故混合储能系统的等效电路如图3 所示。

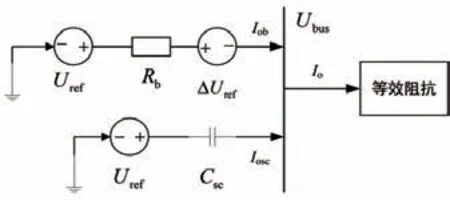
图3 添加补偿电压等效电路结构图

混合储能系统的下垂控制方程为:

根据定义，超级电容的SOC为：

式中：SOC0、Isc和Qc分别为超级电容的初始荷电状态、变换器输入电流和容量。

由式(1)和(3)知，当系统处于稳态时，可得：

式中:t0为暂态启动时间；ts为达到稳态的时间。

忽略超级电容变换器的转换损耗，则超级电容的输入输出功率关系式为UscIsc=UoscIosc，Usc为超级电容端电压，考虑到SOC在暂态过程中变换缓慢，可以假设为常数[4]。

因此，由上述公式可得，当母线电压从因负载突变而波动回到原来的稳定值，超级电容的SOC变化量为：

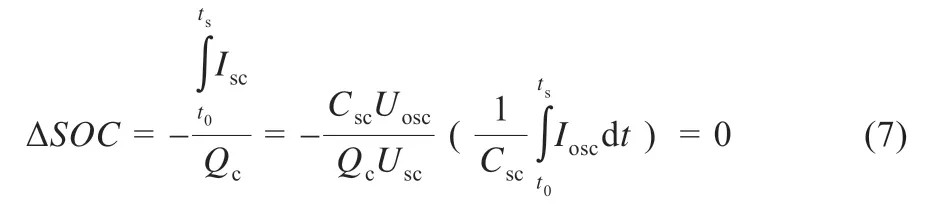
由式(7)可知，超级电容SOC的恢复是随着母线电压恢复而自动实现的，其SOC值在初始值SOC0附近调节，从而完成SOC的恢复。但因为混合储能的功率分配和超级电容器SOC恢复相耦合，所以SOC的恢复可能影响超级电容和蓄电池之间瞬时功率的分配。因此，应该仔细设计系统参数，将影响降至最低。

3 瞬时功率分配与超级电容SOC 恢复的解耦

由式(4)得蓄电池和超级电容器的输出电流表达式为：

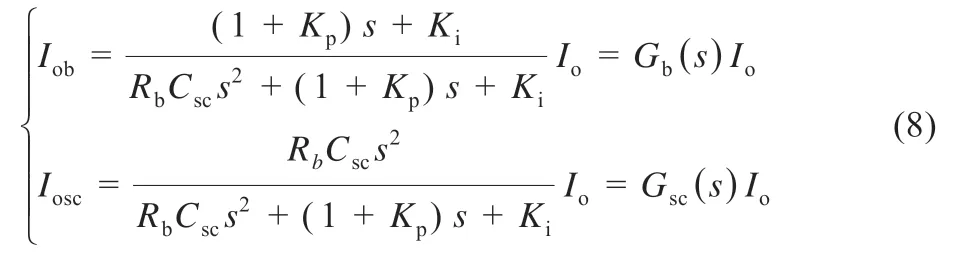
由式(8)可见，进行母线电压补偿后，式(2)中等效的一阶滤波器Gb0(s)和Gsc0(s)变为二阶滤波器Gb(s)和Gsc(s)。超级电容将补偿由Gsc(s)过滤的负载电流，蓄电池补偿由Gb(s)过滤的负载电流。因为超级电容具有快速动态响应能力，并且能够补偿Gsc(s)之后的所有动态电流，所以系统的动态响应由Gsc(s)决定，以确保蓄电池能够处理Gb(s)过滤的所有低频电流。为了将SOC恢复对瞬时功率分配的影响降至最低，应使Gb(s)的截止频率与之前的截止频率ωc相同。

根据截止频率的定义，式(8)中Gb(s)在截止频率ωc处的幅值增益为-3 dB[5]：

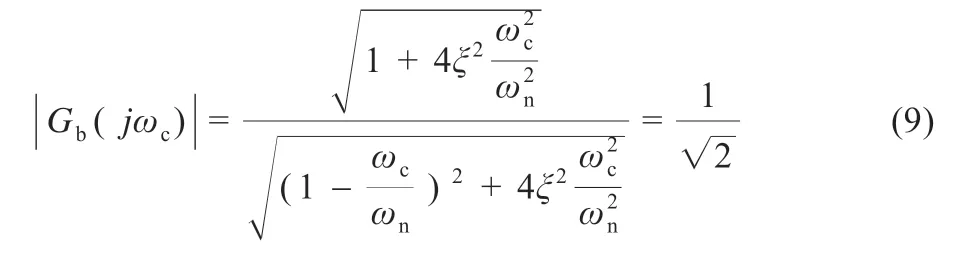
其中，自然频率ωn和阻尼系数ξ 的表达式为：

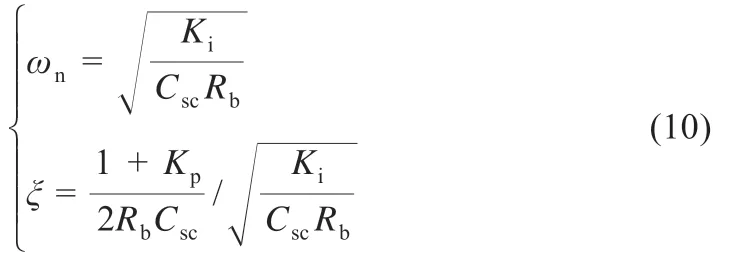
式中：阻尼系数由虚拟电容Csc和电压补偿回路的比例系数Kp决定。为简单起见，Kp可以设置为零。由式(9)和式(10)可得：

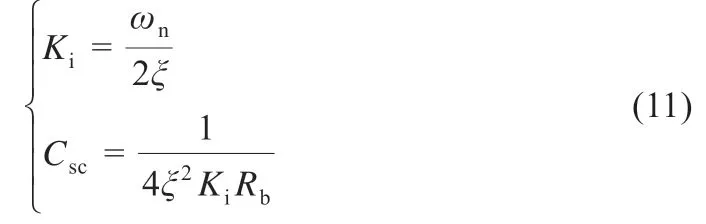
因此，母线电压补偿控制器简化为积分控制器。由式(11)可以得到期望的截止频率和阻尼系数。

图4 示出了基于式(2)和式(8)的Gb0(s)、Gb(s)和Gsc0(s)、Gsc(s)的伯德图，其中Gb(s)、Gsc(s)阻尼比为0.7，截止频率为0.1 Hz，参数Ki和Csc由式(11)设计；Gb0(s)和Gsc0(s)的Csc由ωc和Rb之比获得。如图4(a)所示，Gb(s)和Gb0(s)的截止频率相同并等于截止频率ωc；由图4 可看出，Gb(s)和Gb0(s)允许ωc以下的信号通过，Gsc(s)和Gsc0(s)允许ωc以上的信号通过。因此，负载电流被自动分成由超级电容输出的高频分量和由蓄电池输出的低频分量，从而实现瞬时功率的自动分配。

图4 不具有和具有SOC恢复系统伯德图

由图4(a)可见，SOC在Gb(s)幅度高于0 dB 的范围内进行调节，即蓄电池的电流幅度大于负载电流，这表明此时蓄电池正在给超级电容充电。超过0 dB 的峰值越大，充电或者放电电流就越大，因此SOC恢复速度就越快。由于SOC恢复的频率范围低于截止频率ωc，不会影响混合储能系统的瞬时响应，因此可以实现瞬时功率分配和超级电容器SOC恢复的解耦。

图5 为Gb(s)在阻尼系数ξ 为0.7，截止频率ωc分别为0.1、0.2、0.4、0.6 Hz 时的伯德图。由图可知，在不同截止频率下，Gb(s)的峰值增益都是相同的，这表明当阻尼系数确定之后，蓄电池对超级电容的充电电流相同，所以母线电压和SOC最终的恢复效果相同。但当功率波动时混合储能系统的暂态响应时间由ωc决定，ωc越小，暂态响应时间就越长，超级电容就承担更多的波动功率，但是时间过长不利于系统工作的快速性；ωc越大，暂态响应时间就越短，蓄电池就承担更多的波动功率，超级电容器不能得到充分利用，因此需要折中选取ωc的值。

图5 不同截止频率下的Gb(s)伯德图

所提方法也可用于含有多组混合储能单元的直流微电网。假设混合储能系统中含有m个蓄电池支路和n个超级电容支路，则该系统可以等效为图2 中的单蓄电池和超级电容系统：

式中：RB为混合储能系统的等效虚拟电阻；Csc为混合储能系统等效虚拟电容；Rbi为第i个蓄电池支路的虚拟电阻；Cscj为第j个超级电容支路的虚拟电容。

若新加入一个混合储能单元，则第m+1 个蓄电池支路的虚拟电阻Rb(m+1)为ΔUmax和Iobmax之比，由式(11)可得第n+1 个超级电容支路的虚拟电容Csc(n+1)为：

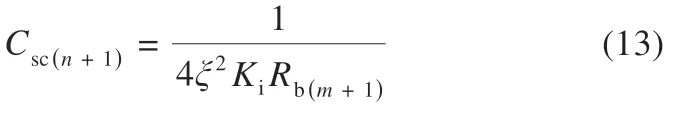
由式(12)可得，添加新的混合储能单元后，系统的等效虚拟电阻和等效虚拟电容为：

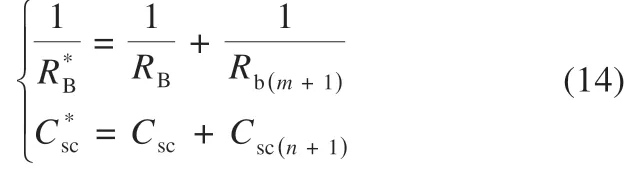
由式(12)～(14)解得：

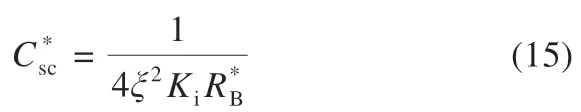
由上式可见，添加新的混合储能单元的等效虚拟电容满足式(11)，故系统的动态特性不变。

4 仿真验证

为了验证所提控制策略和设计准则的有效性，利用MATLAB/Simulink 构建蓄电池和超级电容混合储能系统的仿真模型。系统仿真参数如表1 所示，取不同的截止频率ωc，根据前述设计规则计算出的虚拟电容Csc和积分系数Ki如表2 所示。仿真条件中负载变化均为10 s 时并上80 Ω 电阻，20 s时切除80 Ω 电阻。

表1 系统仿真参数

4.1 混合储能系统瞬时功率分配仿真分析

混合储能系统功率分配仿真波形如图6 所示。图中从上到下分别为蓄电池储能单元输出电流Iob、超级电容储能单元输出电流Iosc、直流母线电压Ubus及超级电容荷电状态SOCsc。由图6 可以看出，在负载突变的情况下，蓄电池和超级电容可以自主承担高低频功率，从而实现瞬时功率分配。负载突变时，超级电容快速响应，蓄电池慢速响应；系统达稳态时，由蓄电池提供稳定的负载电流，超级电容输出电流为零；下垂控制因其自身特性导致实际母线电压与额定母线电压存在偏差；超级电容的荷电状态随负载的变化而变化，且其荷电状态不能回到初始值附近。

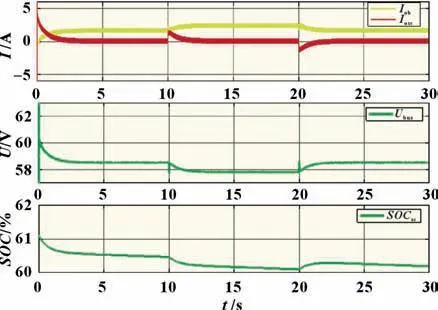
图6 瞬时功率分配仿真波形

4.2 所提控制策略的瞬时功率分配仿真分析

表2 所示情况1、2 的仿真结果分别如图7、图8 所示。从图6 和图7 所示混合储能单元的输出电流波形可以看出，二者的瞬时功率分配几乎相同，而且所提控制策略同样可以实现蓄电池和超级电容的自动功率分配。当负载突增时，Iosc立即增加，然后随着Iob的增加而逐渐减小至零；当瞬时功率分配结束时，母线电压和超级电容SOC恢复过程起主导作用，因此Iosc继续减小到负值，此时表明蓄电池正在给超级电容充电；当系统处于稳态时，虚拟电容相当于断路，所以Iosc最终恢复至零，此时负载电流由蓄电池提供，超级电容不输出电流，母线电压恢复到额定值且超级电容SOC恢复到初始值附近。负载突减时的瞬时功率分配与负载突增时类似，不再赘述。

表2 不同ωc 情况下系统仿真参数

图7 情况1的仿真波形

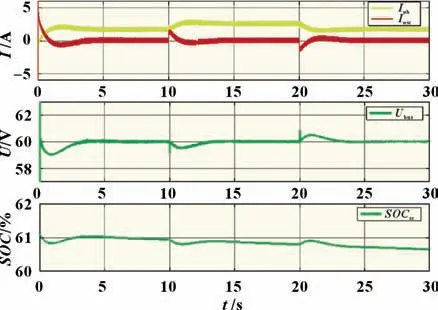
图8 情况2的仿真波形

根据图7 和图8 可以分析阻尼系数不变、截止频率变化对瞬时功率分配的影响。由图7 看出瞬时功率分配耗时1.5 s左右，由图8 可以看出瞬时功率分配耗时约0.8 s 左右。由此可得，瞬时功率分配快慢与截止频率有关，截止频率越大、功率分配响应就越快，截止频率越小、功率分配响应越慢；但动态响应越快超级电容就承担更少的波动功率压力，从而加重了蓄电池承担波动功率的压力；动态响应慢超级电容承担更多波动功率，可以减小蓄电池承担波动功率的压力，但动态响应过慢不利于系统工作的快速性。

5 结论

本文综合考虑混合储能系统功率分配、母线电压补偿以及超级电容SOC恢复问题，提出基于下垂控制和虚拟电压源的混合储能协调控制策略，并利用MATLAB/Simulink 搭建系统仿真模型，通过仿真分析验证了所提控制策略的有效性。仿真结果表明，所提控制策略既能实现混合储能系统功率的自动分配，又稳定母线电压，同时使超级电容SOC恢复到其初始值附近，并实现SOC恢复与瞬时功率分配的解耦。