Cd0.96Zn0.04Te 光致载流子动力学特性的太赫兹光谱研究*

李高芳 廖宇奥 崔昊杨 黄晨光 王晨 马国宏† 周炜 黄志明‡ 褚君浩

1)(上海电力大学电子与信息工程学院,上海 200090)

2)(上海大学物理系,上海 200444)

3)(中国科学院上海技术物理研究所,红外物理国家重点实验室,上海 200083)

采用光抽运-太赫兹探测技术研究Cd0.96Zn0.04Te 的载流子弛豫和瞬态电导率特性.在中心波长800 nm的飞秒抽运光激发下,Cd0.96Zn0.04Te 的载流子弛豫过程用单指数函数进行了拟合,其载流子弛豫时间长达几个纳秒,且在一定光激发载流子浓度范围内随光激发载流子浓度的增大而减小,这与电子-空穴对的辐射复合有关.在低光激发载流子浓度(4.51×1016—1.81×1017 cm–3)下,Cd0.96Zn0.04Te 的太赫兹(terahertz,THz)瞬态透射变化率不随光激发载流子浓度增大而变化,主要是由于陷阱填充效应造成的载流子损失与光激发新增的载流子数量近似.随着光激发载流子浓度继续增大(1.81×1017—1.44×1018 cm–3),THz 瞬态透射变化率随光激发载流子浓度的增大而线性增大,是由于缺陷逐渐被填满,陷阱填充效应造成的载流子损失与光激发新增的载流子数量相比可忽略不计.在光激发载流子浓度为1.44×1018—2.17×1018 cm–3 时,Cd0.96Zn0.04Te 对800 nm 抽运光的吸收达到饱和,THz 瞬态透射变化率不再随光激发载流子浓度增大而变化.不同光激发载流子浓度下Cd0.96Zn0.04Te 在THz 波段的瞬态电导率用Drude-Smith 模型进行了很好的拟合.此研究为碲锌镉探测器的设计和制备提供重要数据支撑和理论依据.

1 引言

碲化镉(CdTe)作为探测器的传感材料,在高能探测领域有着重要的应用.对CdTe 进行锌(Zn)替位掺杂得到的碲锌镉(Cd1–xZnxTe)具有更高的电阻率和更低的暗电流,更适合在室温与低电压环境下工作[1,2],且Cd1–xZnxTe 拥有更高的堆垛层错能和可调的晶格常数,降低了孪晶和位错形成的可能性,提高了热稳定性,并具有优秀的能量识别和光子计数能力,是制备室温高能探测器的首选材料.然而,Zn 替位掺杂会引入新的缺陷,进而影响Cd1–xZnxTe 探测器的性能[3].

目前对Cd1–xZnxTe 的研究主要集中在缺陷对其探测器性能的影响.Guo等[4]利用α 粒子源瞬态电流技术研究了扩展缺陷对Cd1–xZnxTe 晶体电子漂移时间和探测器性能的影响,并采用势垒控制俘获模型解释了扩展缺陷处的载流子俘获机理.Liang等[5]利用光谱成像仪研究了Cd1–xZnxTe 晶体内缺陷浓度对红外吸收边的影响,发现Cd 空位缺陷是影响其红外吸收边斜率的主要原因.Zhao等[6]使用红外光谱分析仪并结合第一性原理研究了本征缺陷对Cd1–xZnxTe 晶体导电类型的影响,发现Cd1–xZnxTe 晶体导电类型的转变与晶体生长过程中形成的Cd 空位缺陷和Cd 间隙缺陷有关.

Cd1–xZnxTe 的载流子迁移率和寿命等载流子动力学特性是设计和制备高性能探测器的重要理论依据[7],然而,目前对Cd1–xZnxTe 载流子动力学特性的研究比较有限.光抽运-太赫兹探测(OPTP)技术是研究半导体超快载流子动力学特性的强有力工具.与传统的THz 时域光谱技术[8]和全光抽运-探测技术[9]相比,OPTP 技术能够提供亚皮秒到纳秒时间尺度上的峰值电导率和瞬态电导率,从而深入了解载流子的性质、迁移率及其时间依赖关系[10];通过扫描THz 时域波形并结合瞬态电导率拟合模型,可以独立地获得光致载流子浓度和迁移率[11];电荷分布随时间变化与迁移率之间的相互作用决定THz 光电导动力学和光谱的形状[12];在这种频率范围和时间分辨率下,测量的THz 瞬态光谱直接反映了超快载流子的运动状态和机制[13,14].

OPTP 技术已经用于研究半导体材料的载流子动力学特性.Yuan等[15]运用光抽运-THz 时域光谱技术系统研究了Te 掺杂GaAsSb 和稀氮化物GaAsSbN 纳米线的非平衡载流子动力学过程,发现氮掺入显著提高了载流子散射速率,并使载流子迁移率大幅降低.Mithun等[16]证明了在使用800 nm 抽运光激发后,Bi2Te3纳米线中存在等离子体振荡,并观察到其峰值电导率Δσ(t)存在一个50 ps 以上的长弛豫过程.Zhang等[17]使用OPTP技术系统地研究了Sb2Se3基异质结中光激发载流子的动态竞争机制,发现带边电子转移和俘获过程的竞争将降低光伏器件的电荷分离效率.文献[18−20]利用OPTP 技术系统地研究了石墨烯与过渡金属二硫化物(TMDs)异质结间的超快电荷转移,发现光激发可以有效地把石墨烯中的电子超快地布局到TMD 导带中,产生电荷分离态.

本文利用OPTP 技术研究Cd0.96Zn0.04Te 的载流子弛豫和瞬态电导率特性.研究发现在光激发载流子浓度为4.51×1016—1.81×1017cm–3时,Cd0.96Zn0.04Te 的THz 瞬态透射变化率基本不随光激发载流子浓度发生变化,当光激发载流子浓度为1.81×1017—1.44×1018cm–3时,其THz 瞬态透射变化率随光激发载流子浓度的增大而线性增大,且在光激发载流子浓度为1.44×1018cm–3时THz 瞬态透射变化率达到最大,继续增大光激发载流子浓度至2.17×1018cm–3时THz 瞬态透射变化率不再发生变化.不同光激发载流子浓度下Cd0.96Zn0.04Te在THz 波段的瞬态电导率用Drude-Smith 模型进行了很好的拟合.此研究为碲锌镉探测器的设计和制备提供重要数据支撑和理论依据.

2 实验

本文使用的OPTP 实验光路系统示意图如图1所示,实验中所用的激光光源是Spectra Physics公司生产的再生放大器(Spitfire Pro),它以振荡器(Mai Tai HP)的飞秒脉冲作为种子光.此放大器的中心波长为800 nm,重复频率为1 kHz,脉冲宽度为120 fs.从放大器发出的光被分束器分为三部分,一部分用于产生THz 波,称为产生光,一部分用于探测THz 波,称为探测光,另外一部分较强的光用于激发样品,称为抽运光,抽运光、探测光和THz 波均为水平偏振.THz 波是由功率约为100 mW、中心波长为800 nm 的光聚焦于厚1 mm、(110)取向的ZnTe 晶体上产生的[21],并通过自由电光取样[22]方法探测.弱的探测光透过厚1 mm、(110)取向的另外一块ZnTe 晶体后进入平衡探测器,接入锁相放大器,通过电脑采集到THz 波信号.通过连续可调衰减片的调节,抽运光激发载流子浓度的变化范围为4.51×1016—2.17×1018cm–3.THz 波光斑直径约为1.5 mm,激发样品的抽运光光斑直径约为6 mm,抽运光光斑直径大于探测光光斑直径的两倍,能够充分保证探测光探测到被抽运光均匀激发样品的部分.整个OPTP 实验在充满N2的湿度为3.8%的室温环境下进行.

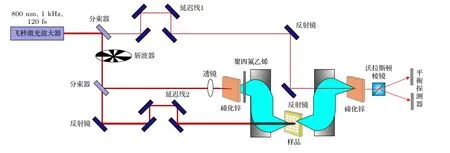
图1 光抽运-太赫兹探测光路示意图Fig.1.Experimental arrangement for optical-pump THz -probe measurements.

实验样品采用垂直布里奇曼法生长,选取高纯(6N)的Te,Cd 和Zn,按Cd0.96Zn0.04Te 的组分称取原料,置于石英安瓿中,真空封装后,放入垂直三段温区的电炉中生长.生长结束后,晶体锭条按(111)面和(211)面切割为厚约1 mm 的晶片[23].此外,CdTe 晶体同样采用垂直布里奇曼法生长,厚约1 mm.

3 结果与讨论

Cd0.96Zn0.04Te 的晶体结构示意图如图2(a)所示,由Cd(Zn)原子与Te 原子各自组成的面心立方亚晶格沿空间对角线位移形成.Cd0.96Zn0.04Te可以看作是CdTe 中Zn 原子占据了晶格点阵中某些Cd 原子的位置,Zn 的占比为0.04.Cd0.96Zn0.04Te室温下的紫外-可见透射光谱如图2(b)的红色实线所示.从图2(b)可以看出,Cd0.96Zn0.04Te 吸收边对应的波长比CdTe(图2(b)中的蓝色虚线所示)更短,其禁带宽度更大,与文献[24]中报道的禁带宽度1.54 eV 基本一致.从图2(b)还可以看出,Cd0.96Zn0.04Te和CdTe 对800 nm(1.55 eV)的光吸收足够大,800 nm 光激发能够使Cd0.96Zn0.04Te和CdTe 中的载流子重新分布.

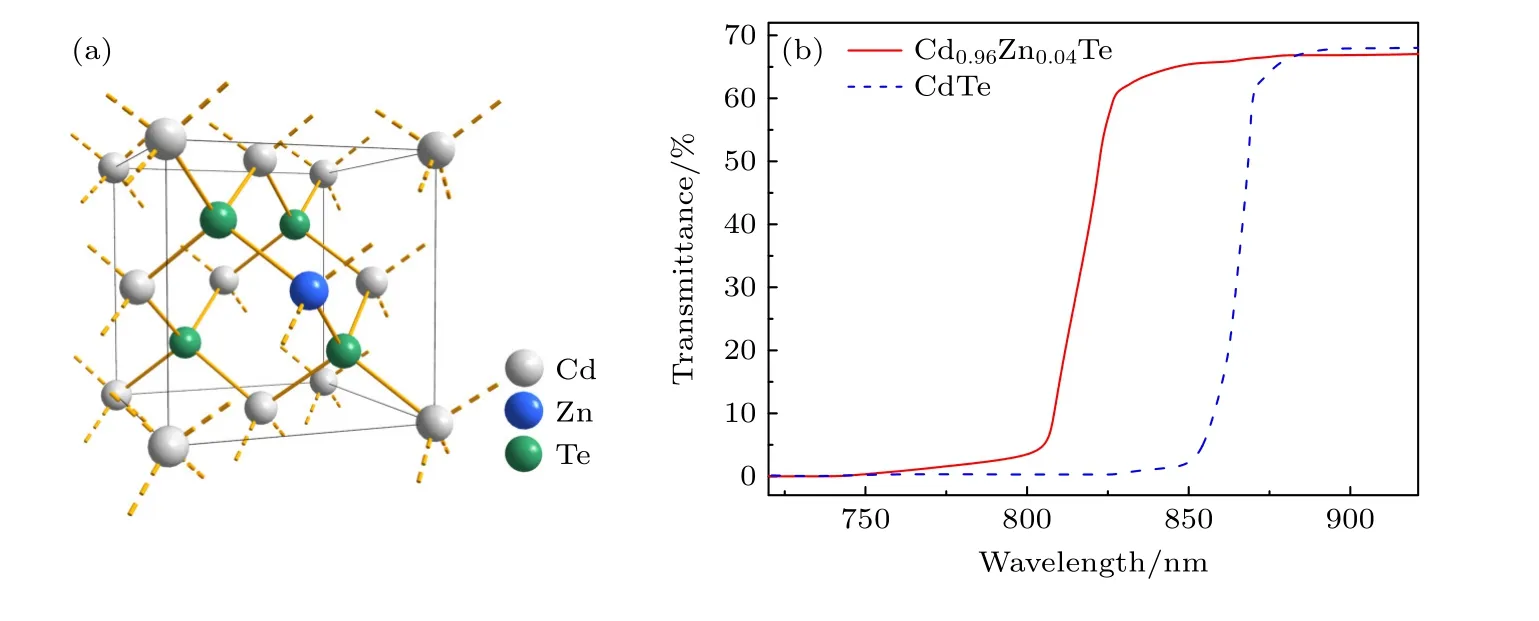
图2 (a)Cd0.96Zn0.04Te 的晶体结构示意图;(b)Cd0.96Zn0.04Te(红)和CdTe(蓝)室温下的紫外-可见透射光谱Fig.2.(a)Crystal structure for Cd0.96Zn0.04Te;(b)the UV-visible transmittance spectra of Cd0.96Zn0.04Te(red)and CdTe(blue)at room temperature.

需要说明的是为了更直观地讨论光激发载流子浓度对Cd0.96Zn0.04Te 载流子弛豫和瞬态电导率的影响,利用N=(1-R)I/(Lhv)[25]换算了不同抽运光强度下的光激发载流子浓度,其中,R是反射率(菲涅耳损耗),Cd0.96Zn0.04Te 的反射率R为0.21[26],I是激发光强度,hv是800 nm 抽运光的光子能量,L为光在样品中的有效穿透深度(趋肤深度),由L=λ/(4πk),k=0.05[27],得到Cd0.96Zn0.04Te的趋肤深度约为1270 nm.

首先,用中心波长为800 nm 的抽运光激发Cd0.96Zn0.04Te,观察不同光激发载流子浓度下THz瞬态透射变化率与延迟时间的关系.图3(a)是不同光激发载流子浓度下Cd0.96Zn0.04Te 的THz 瞬态透射变化率(–ΔT/T0)与延迟时间的关系图,其中,ΔT=T(τ)–T0,T(τ)为有抽运光激发时的THz峰值透射强度随延迟时间的变化,T0为无抽运光激发时的THz 峰值透射强度.由图3(a)可知,在低光激发载流子浓度(4.51×1016—1.81×1017cm–3)下,Cd0.96Zn0.04Te 的THz 瞬态透射变化率基本不随光激发载流子浓度的增大而改变.在光激发载流子浓度为1.81×1017—1.44×1018cm–3时,THz 瞬态透射变化率随光激发载流子浓度的增大而增大.光激发载流子浓度从1.44×1018cm–3继续增大至2.17×1018cm–3时,THz 瞬态透射变化率基本保持不变,是由于Cd0.96Zn0.04Te 对800 nm 抽运光吸收达到饱和,随着光激发载流子浓度的增大,产生的载流子数目不再增加,导致对THz 波的吸收不再发生变化.

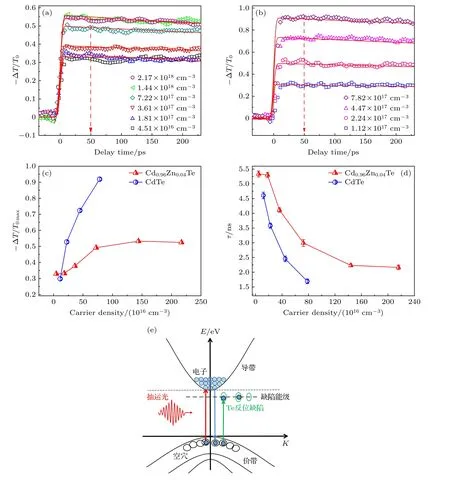
图3 不同光激发载流子浓度下Cd0.96Zn0.04Te(a)和CdTe(b)的THz 瞬态透射变化率与延迟时间的关系图,实线是单指数函数拟合结果;(c)Cd0.96Zn0.04Te 和CdTe 的THz 瞬态透射变化率最大值(–ΔT/T0 max)与光激发载流子浓度的关系图;(d)Cd0.96Zn0.04Te和CdTe 的载流子复合时间与光激发载流子浓度的关系图;(e)Cd0.96Zn0.04Te 的能带结构示意图Fig.3.Transient transmittance change(–ΔT/T0)of THz probe pulse as a function of probe delay with carrier density from 4.51×1016 cm–3 increases to 2.17×1018 cm–3 for Cd0.96Zn0.04Te(a)and with carrier density from 1.12×1017 increases to 7.82×1017 for CdTe(b),solid curves are monoexponential fits;(c)maximum value of the transient transmittance change(–ΔT/T0 max)of THz probe pulse as a function of carrier densities for Cd0.96Zn0.04Te and CdTe;(d)the relationship between relaxation time and carrier density,in which the points with error bars show experimental data and the lines are guide to the eye;(e)the band structure of Cd0.96Zn0.04Te.

从图3(c)的Cd0.96Zn0.04Te(红色曲线)THz 瞬态透射变化率最大值(–ΔT/T0 max)与光激发载流子浓度的关系图也可以看出,在低光激发载流子浓度(4.51×1016—1.81×1017cm–3)时,Cd0.96Zn0.04Te的–ΔT/T0 max基本不随光激发载流子浓度的增大而改变,在光激发载流子浓度为1.81×1017—1.44×1018cm–3时,Cd0.96Zn0.04Te 的–ΔT/T0 max随光激发载流子浓度的增大呈线性增大,光激发载流子浓度从1.44×1018cm–3增大至2.17×1018cm–3时,Cd0.96Zn0.04Te 的–ΔT/T0 max达到最大值且保持不变.

不同光激发载流子浓度下Cd0.96Zn0.04Te 的载流子弛豫过程用单指数函数进行了较好的拟合,其拟合结果如图3(d)的红色曲线所示.从图3(d)的红色曲线可以看出,Cd0.96Zn0.04Te 的载流子复合时间随光激发载流子浓度的增大分别为(5.34±0.05)ns,(5.29±0.04)ns,(4.11±0.02)ns,(2.99±0.06)ns,(2.23±0.07)ns 和(2.16±0.03)ns,其复合时间长达几个纳秒.在低光激发载流子浓度(4.51×1016—1.81×1017cm–3)下,Cd0.96Zn0.04Te的载流子复合时间随光激发载流子浓度的增大变化不明显.在光激发载流子浓度为1.81×1017—1.44×1018cm–3时,Cd0.96Zn0.04Te 的载流子复合时间随光激发载流子浓度的增大呈线性减小.光激发载流子浓度从1.44×1018cm–3继续增大至2.17×1018cm–3时,Cd0.96Zn0.04Te 的载流子复合时间随光激发载流子浓度的增大基本不发生变化,且载流子复合时间最短,约为2 ns.需要说明的是,Cd0.96Zn0.04Te的载流子复合时间远大于数据的有效扫描窗口,主要是由于实验中延迟线长度有限,可以实现的最长扫描时间约230 ps,因此,所有数据采用230 ps 的有效扫描时间窗口.

为了进一步理解Cd0.96Zn0.04Te 的载流子弛豫机理,测量了不同光激发载流子浓度下CdTe 的THz 瞬态透射变化率(–ΔT/T0)与延迟时间的关系,如图3(b)所示.需要说明的是,CdTe 的光激发载流子浓度也由N=(1–R)I/(Lhv)换算得出,其中R=0.23(R=(n–1)2/(n+1)2,n=2.876 是800 nm 波长处的折射率[28]),趋肤深度L=500 nm(800 nm 处的消光系数k=0.125[28]).如图3(c)蓝色曲线所示,CdTe 的THz 瞬态透射变化率最大值(–ΔT/T0 max)随光激发载流子浓度的增大基本呈线性增大,从光激发载流子浓度1.12×1017cm–3时的0.3 左右线性增大至光激发载流子浓度7.82×1017cm–3时的接近1.CdTe 的载流子复合时间也用单指数函数进行了拟合,如图3(d)的蓝色曲线所示,载流子复合时间随光激发载流子浓度的增大依次为(4.61 ± 0.04)ns,(3.58 ± 0.02)ns,(2.46 ±0.05)ns 和(1.69 ± 0.02)ns.其复合时间长达几个纳秒且随光激发载流子浓度的增大呈线性减小,这与文献[29]报道的CdTe 载流子主导复合机制电子-空穴对的辐射复合一致.Cd0.96Zn0.04Te的载流子弛豫过程中没有发现明显的快弛豫现象,并且其复合时间同样长达几个纳秒,在光激发载流子浓度为1.81×1017—1.44×1018cm–3时,Cd0.96Zn0.04Te的载流子复合时间也随光激发载流子浓度的增大线性减小,与CdTe 的载流子弛豫过程类似,因此Cd0.96Zn0.04Te 的载流子复合机制也是以电子-空穴对的辐射复合为主.

在光激发载流子浓度小于1.81×1017cm–3时,Cd0.96Zn0.04Te 的THz 瞬态透射变化率和复合时间几乎不受光激发载流子浓度变化的影响,与Te反位缺陷的陷阱填充效应有关.Cd0.96Zn0.04Te 中Zn—Te 键离子性较弱,比CdTe 中的Cd—Te 键更容易断裂,Zn—Te 键断裂后产生阳离子空位[30],在晶体生长过程中过量的Te 将占据阳离子空位,形成Te 反位缺陷[31],因此,Cd0.96Zn0.04Te 比CdTe拥有更高浓度的Te 反位缺陷[32].图3(e)为Cd0.96Zn0.04Te 的能带结构示意图,Te 反位缺陷作为典型的电子型陷阱[33],能够俘获自由迁移的电子,使其滞留(或局域)在陷阱中直至被填满.当陷阱未被填满时,光激发载流子被缺陷俘获的概率Pc可表示为PcNtδVth[34],其中,Nt为缺陷浓度,δ为缺陷能级的俘获截面,Vth为热迁移速率.由于库仑力作用[35,36],δ随抽运光功率的增大而增大,载流子占据缺陷能级的概率也随之提高.因此,在低光激发载流子浓度(4.51×1016—1.81×1017cm–3)下,电子占据缺陷能级的概率与光激发载流子浓度成正比,陷阱填充效应导致的载流子损失与光激发增加的载流子数量相近,从而使Cd0.96Zn0.04Te 的THz 瞬态透射变化率和载流子复合时间基本不随光激发载流子浓度增大而变化.由于缺陷浓度有限[37],陷阱逐渐被填满后,随着光激发载流子浓度的继续增大,陷阱填充效应造成的载流子损失与光激发新增的载流子数量相比可以忽略不计,因此,在光激发载流子浓度为1.81×1017—1.44×1018cm–3时,THz 瞬态透射变化率随光激发载流子浓度的增大线性增大,载流子复合时间也随光激发载流子浓度的增大线性变化.在光激发载流子浓度为2.17×1018cm–3时Cd0.96Zn0.04Te 对800 nm 抽运光的吸收达到饱和,随着光激发载流子浓度的继续增大,THz 瞬态透射变化率和载流子复合时间不再随光激发载流子浓度增大而变化.

为了进一步探究Cd0.96Zn0.04Te 的光激发载流子动力学机制,计算了Cd0.96Zn0.04Te 和CdTe在抽运光延迟时间为50 ps 时的瞬态电导率.首先测量了抽运光延迟时间为50 ps(图3(a)和图3(b)箭头处)时不同光激发载流子浓度下Cd0.96Zn0.04Te和CdTe 的THz 时域光谱,如图4(a)和图4(b)所示.从图4(a)和图4(b)中观测到Cd0.96Zn0.04Te和CdTe 被抽运光激发时,THz 脉冲峰值减小且发生负的相移,负相移随光激发载流子浓度的增大而增大[38].图4(c)和图4(d)分别是图4(a)和图4(b)经过傅里叶变换后的频谱图,可以看出两者的THz频谱振幅均随光激发载流子浓度的增大而减小.

接下来计算Cd0.96Zn0.04Te 和CdTe 在抽运光延迟时间为50 ps 时的瞬态电导率.把没有抽运光激发时的THz 光谱作为参考信号、有抽运光激发时的THz 光谱作为样品信号,瞬态电导率随频率的变化关系式为[39]

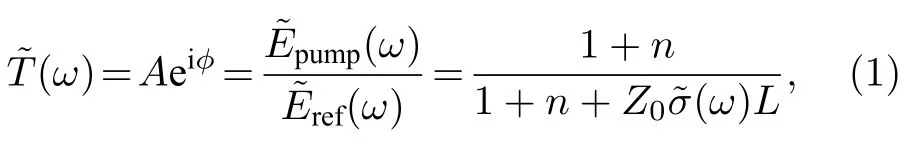
其中A是有抽运光激发和无抽运光激发时THz 信号在频谱上的强度之比,φ是有抽运光激发和无抽运光激发时样品的相位差,Z0=377 Ω 是自由空间阻抗,L是趋肤深度,n是无抽运光激发时样品的折射率.图4(e)为无抽运光激发时Cd0.96Zn0.04Te和CdTe 的折射率图,可以看出两样品的折射率随频率增大略微增大,主要是受到2.1 THz 处二阶声子峰的影响[40],但此声子峰对折射率的贡献比较有限.从0.4—1.5 THz,Cd0.96Zn0.04Te 和CdTe的折射率仅增大了0.06,折射率随频率增大分别约为1.9%和1.8%.并且两样品的其他声子峰[41−43]均远离0.4—1.5 THz 波段,因此可以近似认为两样品的折射率与频率无关.本文选取该频率区间折射率的平均值,分别为3.18 和3.24,与文献[40,44]中报道的折射率接近.Cd0.96Zn0.04Te 和CdTe的瞬态电导率分别如图5(a)和图5(b)所示,两个样品的瞬态电导率实部均随光激发载流子浓度的增大而增大,且在不同光激发载流子浓度下瞬态电导率的实部都是正的,均随频率的增大而增大,虚部都是负的.此外,虽然在2.1 THz 处CdTe 存在二阶声子峰[40],但二阶声子效应对电导率的贡献非常小,为简单起见,在电导率拟合中忽略了2.1 THz处的二阶声子效应对0.4—1.5 THz 波段瞬态电导率的影响.因此,选用Drude-Smith 模型对电导率的实部和虚部进行拟合,其表达式为[45]

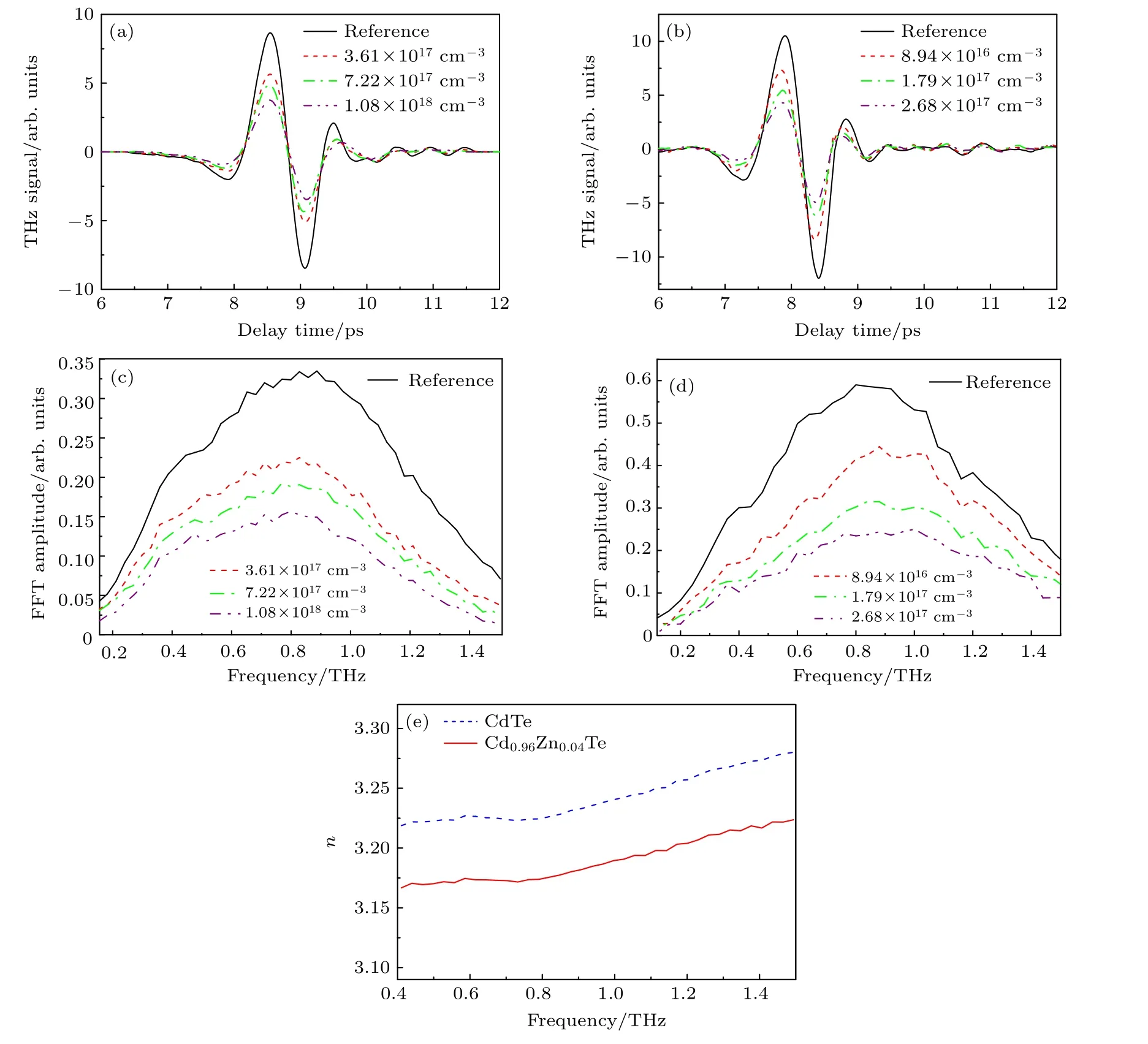
图4 不同光激发载流子浓度下Cd0.96Zn0.04Te(a)和CdTe(b)的THz时域谱;傅里叶变换后不同光激发载流子浓度下的Cd0.96Zn0.04Te(c)和CdTe(d)的频谱图;(e)无抽运光激发时Cd0.96Zn0.04Te 和CdTe 的折射率图Fig.4.THz time domain spectroscopy of Cd0.96Zn0.04Te(a)and CdTe(b)with different carrier densities;THz spectrum of Cd0.96Zn0.04Te(c)and CdTe(d)with different carrier densities;(e)refractive index of nonphotoexcited Cd0.96Zn0.04Te and CdTe in THz frequency with no pump.

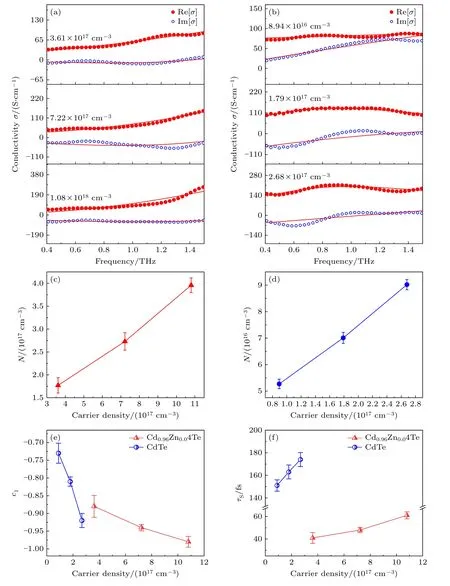
图5 不同光激发载流子浓度下Cd0.96Zn0.04Te(a)和CdTe(b)的瞬态电导率,实线为Drude-Smith 模型的拟合结果;延迟时间为50 ps 时Cd0.96Zn0.04Te(c)和CdTe(d)的载流子浓度随光激发载流子浓度的变化关系;(e)Cd0.96Zn0.04Te(红)和CdTe(蓝)的Smith 参数c1 随光激发载流子浓度的变化关系图;(f)Cd0.96Zn0.04Te(红)和CdTe(蓝)的载流子散射时间τS 随光激发载流子浓度的变化关系图Fig.5.The THz photoconductivities of Cd0.96Zn0.04Te(a)and CdTe(b)at different photogenerated carrier density,solid lines show the fitting results of the Drude-Smith model;the relationship between carrier concentration and photoexcited carrier concentration at 50 ps delay time of Cd0.96Zn0.04Te(c)and CdTe(d);(e)the relationship of Smith parameterc1 with photogenerated carrier concentration of Cd0.96Zn0.04Te(red)and CdTe(bule);(f)the carrier scattering timeτS varies with the photogenerated carrier concentration of Cd0.96Zn0.04Te(red)and CdTe(bule).

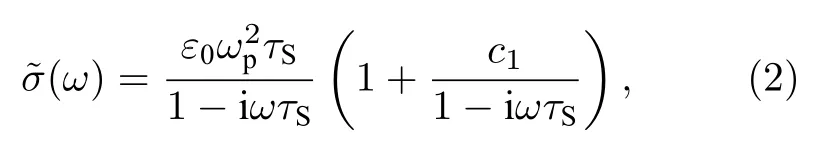
根据拟合结果得到了延迟时间为50 ps 时的载流子浓度N,如图5(c)和图5(d)所示.在光激发载流子浓度为3.61×1017,7.22×1017,1.08×1018cm–3条件下,Cd0.96Zn0.04Te 在延迟时间为50 ps 时的载流子浓度分别为(1.77±0.16)×1017,(2.73±0.19)×1017和(3.96±0.17)×1017cm–3;在光激发载流子浓度为8.94×1016,1.79×1017,2.68×1017cm–3时,CdTe 载流子浓度分别为(5.27±0.19)×1016,(7.01±0.21)×1016,(9.02±0.17)×1016cm–3.拟合得到的载流子浓度低于光激发载流子浓度,主要是由于与频率相关的瞬态复电导率是在抽运光延迟时间约为50 ps 时获得的,此时光激发产生的部分载流子已经复合.图5(e)是Cd0.96Zn0.04Te 和CdTe 的Smith参数c1与光激发载流子浓度的关系图.从图5(e)可以看出,当光激发载流子浓度由3.61×1017cm–3增大至1.08×1018cm–3时,Cd0.96Zn0.04Te的c1从–0.88±0.03 下降到-0.98±0.02,接近–1.CdTe 在光激发载流子浓度为8.94×1016—2.68×1017cm–3时,c1依次为–0.73±0.03,–0.81±0.02 和–0.92±0.01.两样品的c1值均随光激发载流子浓度增大而减小,说明两样品的载流子运动均不是自由散射,都有不同程度的局域或背向散射.当载流子作散射运动时,载流子浓度越高,碰撞概率越大,载流子散射时间τS越小.图5(f)是不同光激发载流子浓度下Cd0.96Zn0.04Te 和CdTe 的载流子散射时间τS的拟合结果图.由图5(f)可知,随着光激发载流子浓度的增大Cd0.96Zn0.04Te 的散射时间τS(红色曲线)从(41±5.61)fs 逐渐延长到(61±3.23)fs,CdTe的τS(蓝色曲线)也从(151±5.2)fs 逐渐延长到(174±6.91)fs,这说明两样品的载流子运动不是背向散射,而是受到了不同程度的局域,并且局域程度随光激发载流子浓度的增大而增强.

从图5(e)还可以看出,在光激发载流子浓度为1.08×1018cm–3时Cd0.96Zn0.04Te的c1值接近–1,说明在一定光激发载流子浓度下Cd0.96Zn0.04Te的光激发载流子可以完全被局域.从图5(f)还可看出,Cd0.96Zn0.04Te 的载流子散射时间远小于CdTe的,载流子的散射时间和迁移率成正比[46],因此Cd0.96Zn0.04Te 的载流子迁移率远小于CdTe 的.

4 结论

本文采用光抽运-太赫兹探测技术研究Cd0.96Zn0.04Te 的光致载流子动力学特性.在800 nm 飞秒抽运光激发下Cd0.96Zn0.04Te 的载流子弛豫过程用单指数函数进行了拟合,其载流子弛豫时间长达几个纳秒,且在一定光激发载流子浓度范围内随光激发载流子浓度增大而减小,这与电子-空穴对的辐射复合有关.Cd0.96Zn0.04Te 的THz 瞬态透射变化率在低光激发载流子浓度(4.51×1016—1.81×1017cm–3)下几乎不变化,这主要是由于在晶体生长过程中加入了过量的Te,形成Te 反位缺陷,缺陷的陷阱填充效应造成的载流子损失与光激发新增的载流子数量近似.随着光激发载流子浓度继续增大(1.81×1017—1.44×1018cm–3),大部分缺陷被占据,由于陷阱填充效应导致的载流子损失与光激发新增的载流子数量相比可以忽略不计,因此THz瞬态透射变化率随光激发载流子浓度的增大而增大.在光激发载流子浓度高于1.44×1018时,Cd0.96Zn0.04Te 对800 nm 抽运光吸收达到饱和,THz 瞬态透射变化率不再随光激发载流子浓度增大而变化.不同光激发载流子浓度下Cd0.96Zn0.04Te 在THz波段的瞬态电导率用Drude-Smith 模型进行了较好的拟合,拟合结果显示Cd0.96Zn0.04Te 的载流子运动不是背向散射而是被缺陷局域,局域程度随光激发载流子浓度的增大而增强,且Cd0.96Zn0.04Te的载流子迁移率远小于CdTe 的.结果表明,在Cd1–xZnxTe 生长中严格控制Te 的含量,将在一定程度上抑制Te 反位缺陷的形成[31],减小光生载流子损失,提高载流子迁移率.此研究为碲锌镉探测器的设计和制备提供重要数据支撑和理论依据.