石墨烯电极弯折对2-苯基吡啶分子器件负微分电阻特性的调控和机理*

邢海英 张子涵 吴文静 郭志英 茹金豆

1)(天津工业大学电子与信息工程学院,天津 300387)

2)(中国科学院高能物理研究所,多学科研究中心,北京 100049)

3)(大功率半导体照明应用系统教育部工程研究中心,天津 300387)

4)(鸿之微科技(上海)股份有限公司,上海 200120)

采用非平衡格林函数结合密度泛函理论探讨了以锯齿型石墨烯纳米带为电极、2-苯基吡啶分子为中心区的分子器件电子输运性质.分析I-V 特性及透射谱随偏压的变化表明,电极弯折能够调控器件负微分电阻特性,使器件峰值电压(Vp)减小、电流峰谷比(PVR)增大,当电极弯折角度为15°时,器件获得低峰值电压(0.1 V)、高电流峰谷比(12.84)的负阻特性.平衡态下器件的透射谱、态密度、散射态实空间分布图及投影态密度解释了器件负阻特性被调控源于电极弯折使器件中心分子与电极间的波函数交叠发生变化,导致两者间耦合减弱.弱耦合下外加偏压后,器件的透射系数因能级移动和偏压的变化而产生大幅波动,使器件在低偏置电压处即出现大的透射系数,产生峰值电流Ip,降低了器件的Vp,且增大了PVR 值,其所获得的低Vp、高PVR 的负阻特性在低功耗分子电子领域具有潜在的应用前景.

1 引言

利用分子器件实现传统电子元件的基本功能已被认为是分子电子学的研究目标[1−3],因而该研究领域备受关注,并发现了许多有趣的物理特性,如分子整流[4,5]、分子开关[6,7]以及负微分电阻(negative differential resistance,NDR)特性[2,8,9]等.NDR是Esaki 二极管和共振隧穿二极管(resonant tunneling diode,RTD)的基本特性[10],应用于模数转换器、高频振荡器及逻辑电路中[10−12],使用RTD能够大幅降低动态随机存取存储器(DRAM)的储用功率.Chen等[13]研究表明,具有NDR 特性的分子器件可用于实现极低静态功耗和极高密度的存储单元,有望替代III-V 化合物半导体器件,为此许多研究人员为之付出不断的努力并获得大量研究成果[14−19].此外,Berg等[20]研究指出,具有低偏压、高峰谷电流比(peak-valley ratio,PVR)的分子NDR 器件可用于DRAM 记忆单元的局域刷新.因此,低偏压、高PVR 的分子NDR 器件具有广阔的应用前景.

为获得具有应用价值的分子NDR 器件,一方面要探寻具有优良特性的中心分子,另一方面也需探索电极对分子器件输运特性产生的影响.实验研究表明[21,22],芳香分子的导电性与其内禀芳香性负相关,吡啶分子中含有的氮元素降低了分子的芳香性,提高了其导电性.因此,基于吡啶环的分子器件研究引起广泛关注,并观察到其具有NDR 传输特性[14,15,17,23].2015 年《半导体国际技术路线图》将石墨烯纳米带(GNR)列为具有弹道传输、电迁移电阻等优良特性的互连材料[19],且具有平面结构的GNR 可适用于多种电子器件的制备工艺[24,25],GNR 也因此被认为可用于分子器件的电极[18,19,26,27].Li等[28]也发现,以锯齿型石墨烯纳米带(ZGNR)为电极的共轭吡啶端分子器件较某些金属和二维石墨烯电极更具优越性.此外,科学家们发现仅通过控制石墨烯形变状态即可调控其输运特性[29],而其所具有的高柔韧性又使得改变基于石墨烯的纳米器件形状成为可能[30],并实现了器件输运特性的调控[31,32].本文以2-苯基吡啶分子为中心区分子,以ZGNR 为电极构建分子器件,采用非平衡格林函数(NEGF)结合密度泛函理论(DFT)探究ZGNR 电极弯折对器件NDR 特性的调控作用,探讨获得低偏压、高PVR 的分子NDR 器件物理规律,以期为深入理解分子器件电子输运特性及其调控和实际应用提供有益的参考.

2 计算模型与方法

图1 为2-苯基吡啶分子器件结构图,器件由中心散射区和左、右电极三部分构成.如图所示,中心散射区由2-苯基吡啶分子构成,左、右电极均选择宽度为3 的ZGNR,2-苯基吡啶分子与ZGNR是通过碳-碳键相耦合,因此模型具有高对称性;器件中设置5 层石墨烯缓冲层以屏蔽电极对中心区的影响,电极的悬挂键由氢原子钝化.为研究石墨烯电极弯折对器件电子输运特性的影响,根据器件左、右电极的弯折角度15°,30°和45°构建模型,并据此将模型分别命名为M1(0°),M2(15°),M3(30°)和M4(45°).文中模型结构优化和电子输运特性计算分别由VASP 软件包[33,34]和基于DFT 结合NEGF 的Nanodcal[35]完成.器件结构优化采用投影缀加平面波(projector augmented wave,PAW)方法,交换关联泛函选择LDA_PZ81,平面波的截断能为500 eV,力的收敛标准为0.02 eV/Å.在输运性质计算过程中,采用原子轨道线性组合(LCAO)基组,交换关联泛函选择LDA_PZ81,价电子轨道描述选用双极化DZP 基组,截断能为80 Hartree,z方向为器件的输运方向,x与y方向为真空层(厚度20 Å)以屏蔽器件周期性影响,布里渊区采样用Monkhorst-Pack方案进行,k点网络分布为1×1×10,能量的收敛标准为1×10–5eV.

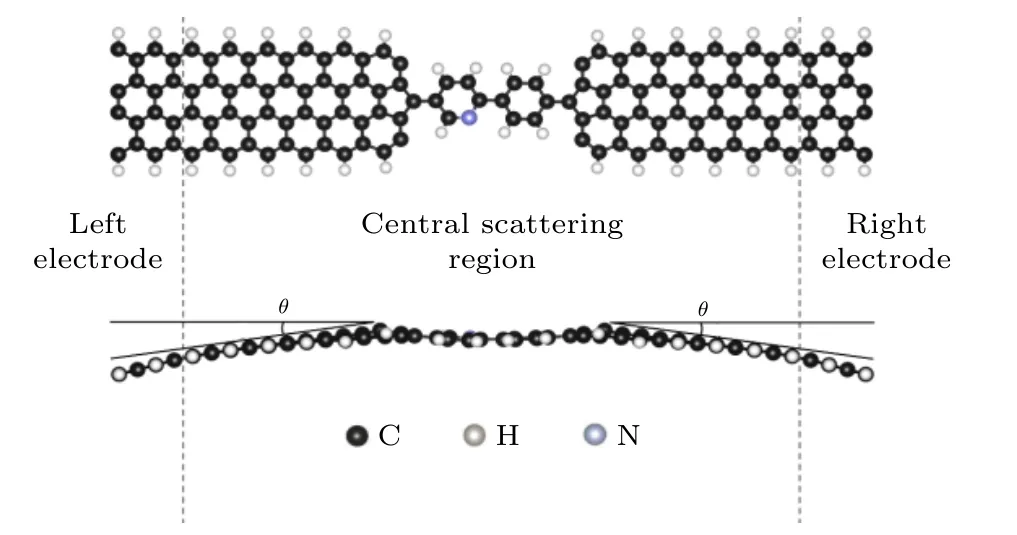
图1 2-苯基吡啶分子器件结构图,图中所示θ 为石墨烯电极弯折角度Fig.1.Structure diagram of the 2-phenylpyridine molecular device,θ represented to the bending angle of the graphene electrode.

通过器件的电流可由Landauer-Büttiker 公式计算得出[36,37],即:

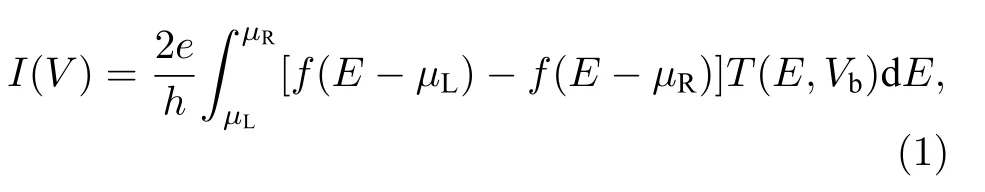
式中,e为电子电荷;h为普朗克常数;f(E)为费米分布函数;µLEf-eV/2与µREf-eV/2分别为左右电极的化学势;[µL(Vb),µR(Vb)]为贡献积分电流的能量区间,称其为偏压窗或积分窗;设Ef为0 则[–Vb/2,+Vb/2]为偏压窗区间;T(E,Vb)为透射函数,表示在外加偏压Vb下能量为E的电子通过体系的概率.因此,计算出电子透过体系的透射函数,即可求出通过体系的电流,其可由(2)式计算[38]:

式中,GR和GA分别为中间传导电子的延迟、提前格林函数,ΓL和ΓR分别为中间传导分子与左、右电极的耦合函数.

3 计算结果与讨论

图2 为器件M1—M4 外加偏压下的I-V特性图.如图2(a)所示,偏置电压小于0.6 V 时,通过器件M1 的电流随电压增大而增大,偏置电压在[+0.6 V,+1.0 V]区间,电流则随电压增加而快速减弱,呈现负微分电阻特性;如图2(b)—(d)所示,器件M2—M4 分别在电压大于0.1 V(M2),0.2 V(M3)和0.1 V(M4)时,电流随偏压增大而大幅减小,当偏压分别增至0.5 V(M2)和0.6 V(M3 与M4)后,电流再次逐渐增强.ZGNR 电极弯折后,器件M2—M4 在低外加偏压处呈现负阻特性,其对应的电压区间分别为[+0.1 V,+0.5 V],[+0.2 V,+0.6 V]和[+0.1 V,+0.6 V].电极弯折使器件负阻特性的电压区间向低偏压移动,且NDR 曲线表现更明显、清晰.

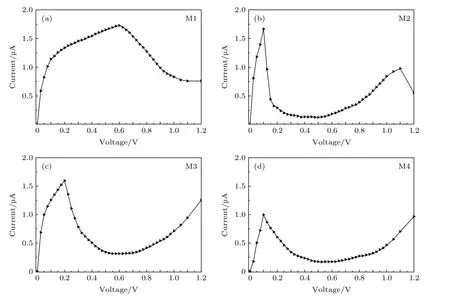
图2 器件M1−M4的I-V 特性曲线图Fig.2.I-V characteristic curves of device M1−M4.

表1 列出了器件M1—M4 负阻峰的峰值电流(Ip)、谷值电流(Iv)、峰谷电流比(PVR)及峰值电压(Vp)等参数.由表中数据可知,相较于器件M1的Vp值0.6 V,电极弯折后器件M2—M4的Vp值均降低,分别为0.1 V(M2),0.2 V(M3)和0.1 V(M4),同时PVR 值由M1 的2.08 分别增大至M2的12.84,M3 的5.16 和M4 的5.82.综上所述,ZG NR 电极弯折调控了器件负阻特性,使器件的PVR值增大,Vp值降低,提升了器件的负阻性能.其中电极弯折角度为15°时,即器件M2 的PVR 值最大为12.84,Vp值为0.1 V,其所获得的0.1 V 的低Vp可以满足实际应用[16].

表1 器件M1−M4的Ip,Iv,PVR和VpTable 1.Ip,Iv,PVR andVp of devices M1−M4.

由(1)式和(2)式可知,透射谱曲线T(E,Vb)在偏压窗内的积分面积决定了通过器件电流I的强弱,因此,随外加偏压变化的透射谱是对I-V特性最直接的物理解释.根据图2中I-V特性,选取与负阻特性相关的特征电压计算器件的透射谱.图3 为偏置电压在+0.1V,+0.2V,+0.5V,+0.6V,+0.8V和+1.0V时器件M1—M4的透射谱图,设Ef为能量参考点,则[–Vb/2,+Vb/2]为偏压窗即图中蓝色线内区域,图中标出了偏压窗内透射谱曲线的积分面积值.如图3 所示,器件M1 在负阻特性[+0.6 V,+1.0 V]区间内,随电压增加偏压窗内透射谱积分面积不断减小,对应的电流也减弱(如图2(a)所示).在此区间内电压为+0.6 V 时积分面积最大,达到0.017 对应M1 的峰值电流.ZGNR 电极弯折后,器件M2 在低偏压+0.1 V 下积分面积即达到M1 在+0.6 V 时的面积0.017,此后积分面积随偏压增大而快速减小,增至+0.5 V时面积最小,随后,积分面积随电压增大而再次增大.因此,在[+0.1 V,+0.5 V]区间M2 呈现NDR特性(如图2(b)所示),在此区间内电压为+0.1 V时积分面积最大,对应M2 的峰值电流.器件M3和M4 呈现与器件M2 相似的变化,分别在[+0.2 V,+0.6 V]和[+0.1 V,+0.6 V]电压区间内积分面积逐渐减小,电流逐渐减弱,表现出NDR 特性,对应的Vp值处曲线积分面积最大.根据(1)式透射谱T(E,Vb)在偏压窗内的积分面积是由透射系数和偏压窗区间大小决定的.分析图3 结果可知,1)随外加偏压增加偏压窗的区间增大,但偏压窗内曲线积分面积却减小,通过器件的电流减弱,说明器件M1—M4 的NDR 特性源于透射系数减小;2)器件M2—M4 分别在低偏压0.1 V 和0.2 V 处(偏压窗区间小)即产生大的积分面积获得峰值电流Ip是源于此处透射系数大,由此也说明了ZGNR 电极弯折调控了NDR 特性,使器件的峰值电压Vp减小、PVR 值增大,NDR 对应的电压区间向低偏压方向移动.

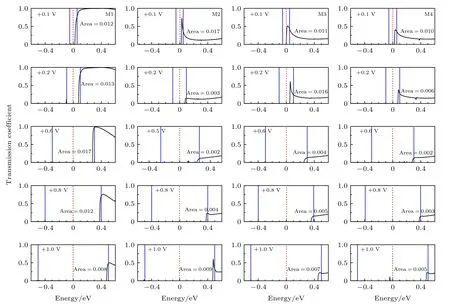
图3 器件M1—M4 在偏置电压为+0.1 V,+0.2 V,+0.5 V,+0.6 V,+0.8 V 和+1.0 V 时的透射谱图,红色虚线为Ef 能级,蓝色线为偏压窗区间Fig.3.Transmission spectra of M1−M4 under the bias voltage of +0.1 V,+0.2 V,+0.5 V,+0.6 V,+0.8 V and +1.0 V,the red dashed line represented to the Fermi level,the blue line represented to the bias window interval.

为深入阐述电极弯折对器件NDR 特性的影响,文中给出平衡态下器件的透射谱、态密度及散射态实空间分布图.图4 为平衡态下(Vb=0)器件M1—M4 的透射谱图.如图4(a)—(d)所示,器件M1在Ef附近[0,1.5 eV]有高且宽的透射峰,说明其具有强的电子输运能力;ZGNR 电极弯折后,器件M2—M4在Ef附近的透射峰变成窄的尖峰,对应能量区域的透射系数减小.由于器件的中心分子与电极间的耦合强弱决定了透射峰的宽度[39],耦合越弱则透射谱的共振透射峰越窄[40,41],即器件M2—M4 的2-苯基吡啶分子与ZGNR 电极间的耦合较M1 减弱,因而表现出透射峰变窄、透射系数减小.另一方面,由态密度能够获得能级E处中心分子与电极间耦合强弱的信息[2,8],即Ef处器件态密度值越小则中心分子与电极间的耦合越弱[42].图5 为器件M1—M4 的态密度图,如图5(a)中插图所示,器件M2—M4在Ef处的态密度值均较器件M1 减小,说明电极弯折后器件M2—M4 的中心区2-苯基吡啶分子与ZGNR 电极间的耦合减弱,这与Ef附近透射谱峰变窄、透射系数减小相符.如图5(a)所示,ZGNR 电极的弯折不仅减弱了器件在Ef处的态密度,同时影响了Ef以上的占据态和以下的未占据态,使Ef附近表现出更多更强的局域特性,而电子态的强局域性会使器件中心分子与电极间的耦合减弱[28].图5(b)为平衡态下器件M1—M4在Ef处延器件传输方向的散射态实空间分布图,如图所示,器件具有一条传输通道,与平衡态下器件透射谱具有一个共振透射峰相符(见图4),其中器件M1 整个结构表现出离域的散射态;因ZGNR 电极弯折,器件M2—M4 则表现出散射态更多地局域在器件左侧,器件右侧特别是右电极的散射态减弱,该图直观地说明了电极弯折使器件中的电子态表现更强的局域性.综上分析可知,ZGNR 电极弯折后器件中心区2-苯基吡啶分子与ZGNR 电极间的耦合减弱.

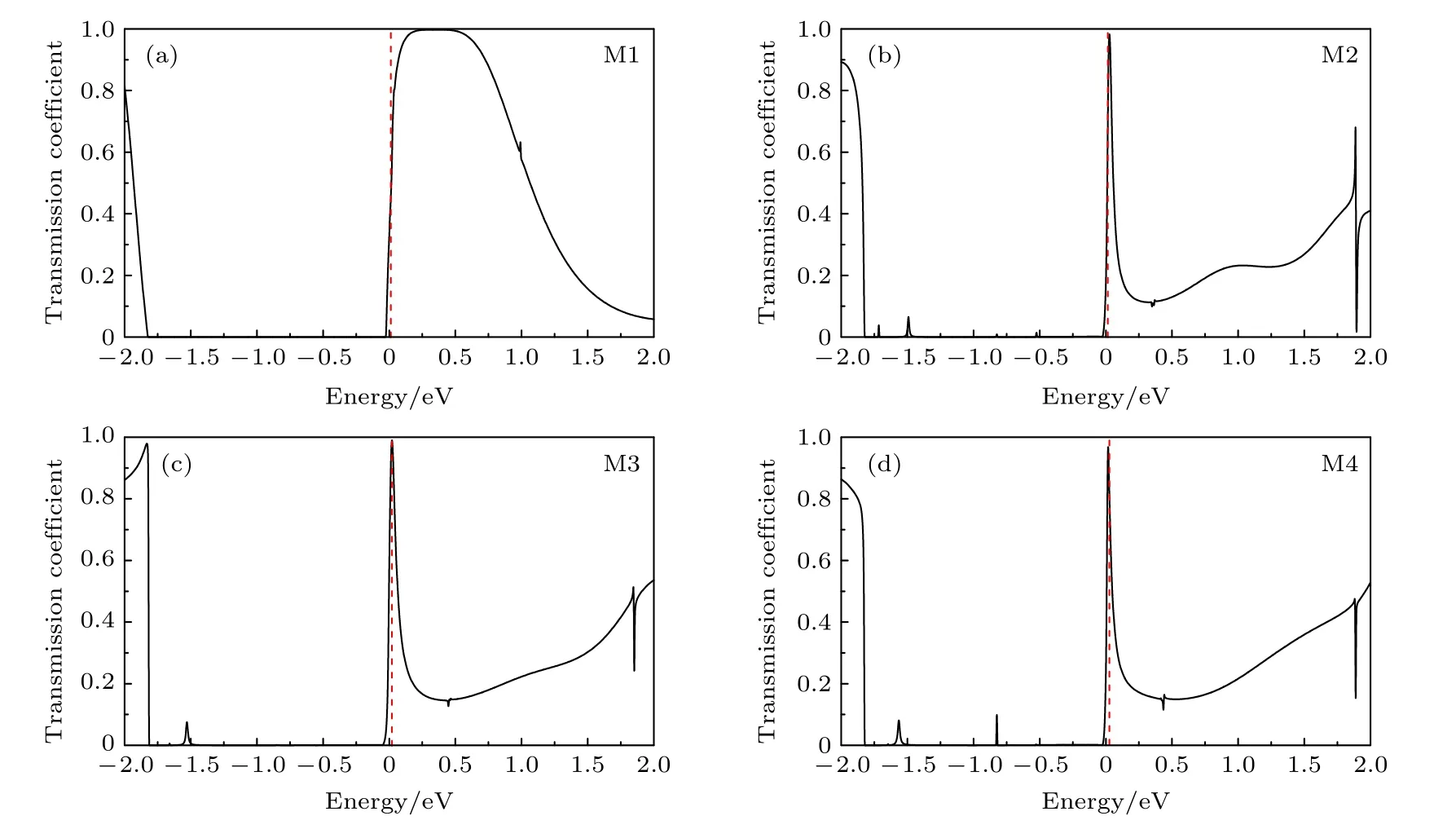
图4 平衡态下(Vb=0)器件M1—M4 的透射谱图,红色虚线为Ef 能级Fig.4.Transmission spectra of device M1−M4 under zero bias(Vb=0),the red dotted line represented to the Fermi level.

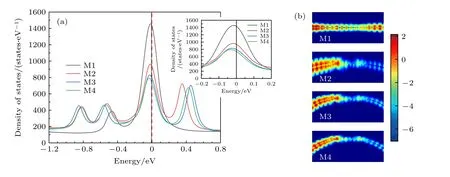
图5 平衡态下(Vb=0)器件M1—M4 的态密度图(a)及Ef 处的实空间散射态分布图(b)Fig.5.Density of states(a)and the real-space scattering states distribution atEf(b)under zero bias(Vb=0)of device M1−M4.

为探讨器件中心分子与电极间耦合力减弱的主因,文中计算了平衡态Ef处ZGNR 电极、2-苯基吡啶分子的投影态密度,列于表2.如表中数据所示,电极弯折后器件M2—M4 态密度降低值中ZGNR 电极的贡献远大于2-苯基吡啶分子的,因此Ef处器件总态密度减小主要来自ZGNR 电极的态密度,而2-苯基吡啶分子的不构成其主要因素.由于文中器件模型具有高对称性,各器件的中心分子及电极材料相同,且左、右两电极的弯折角度相同,弯折方向对称(如图1 所示),因此ZGNR电极弯折改变了中心分子与电极间的电子相互作用,使两者间的波函数交叠发生变化是器件中心2-苯基吡啶分子与电极间耦合减弱的主因.

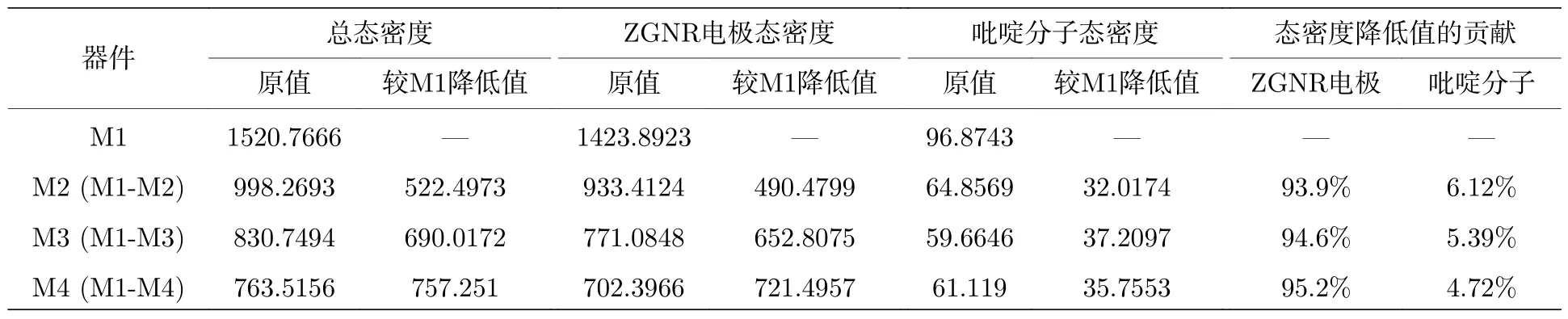
表2 平衡态下器件电极和中心分子在Ef 处投影态密度值及其在总态密度降低值的贡献Table 2.Projected density of states under zero bias(value and percentage in M1−M4)on electrode and 2-phenylpyridine atEf.

研究表明[43],弱耦合下的透射系数会随外加偏压的变化在不同能级间产生大幅波动.一方面,外加偏压会引起能级移动,另一方面,与波函数交叠相关的透射系数对外加偏压变化敏感,且器件中心分子与电极间波函数交叠的变化反映了两者间耦合的强弱[8,43,44].由于ZGNR 电极弯折使器件中心分子与电极间的耦合减弱,在弱耦合条件下,外加偏压后器件的透射系数则因能级的移动和偏压的变化而产生大幅波动,故器件M2—M4 在外加低偏置电压(0.1 V 或0.2 V)处即出现大的透射系数,使电流大幅增强,获得峰值电流Ip,降低了器件的Vp值,且增大了PVR 值,NDR 特性对应的电压区间向低偏压方向移动.表3 为器件M1—M4在偏置电压分别为零偏压,+0.1 V,+0.2 V,+0.5 V(M2),+0.6 V(M1,M3与M4)和+1.0V下散射态实空间分布图(与图5(b)共用色坐标).如表中散射态图所示,在外加偏压下器件均有一个传输通道,与图3 中透射谱在各偏压窗内具有一个共振透射峰相符.器件M1 的外加偏压由+0.1 V 经+0.2 V增至+0.6 V 过程中,整个器件结构均具有强且均匀的散射态,表明散射态由左电极经中心分子导通至右电极,在+0.6 V 处散射态最强,器件M1 在此处透射谱积分面积最大,获得峰值电流Ip(如图3所示);当偏压增至+1.0 V 时,M1 右侧散射态减弱,此处透射谱积分面积最小,对应器件M1 的峰谷电流Iv.ZGNR 电极弯折且外加偏压后,零偏压下局域在器件M2—M4 左电极的散射态导通至右电极,并分别在+0.1 V(M2),+0.2 V(M3)和+0.1 V(M4)处表现强且均匀的散射态,相应电压处3 个器件具有峰值电流Ip,透射谱积分面积也最大;当偏压分别增至+0.5 V(M2)和+0.6 V(M3,M4)时器件M2—M4 右侧散射态减弱,即从器件左侧导通至右侧的散射态减少,器件在此电压处出现峰谷电流Iv,透射谱积分面积也最小;当偏压继续增至+1.0 V,器件M2—M4 右侧散射态表现增强,器件电流再次增大,透射谱积分面积也增加.表中散射态图直观地说明了ZGNR 电极弯折后各器件在外加偏压下I-V特性和透射谱的变化过程,同时结合前述分析解释了因ZGNR 电极弯折使器件Vp值减小,PVR 值增大,负阻特性被调控的机理.

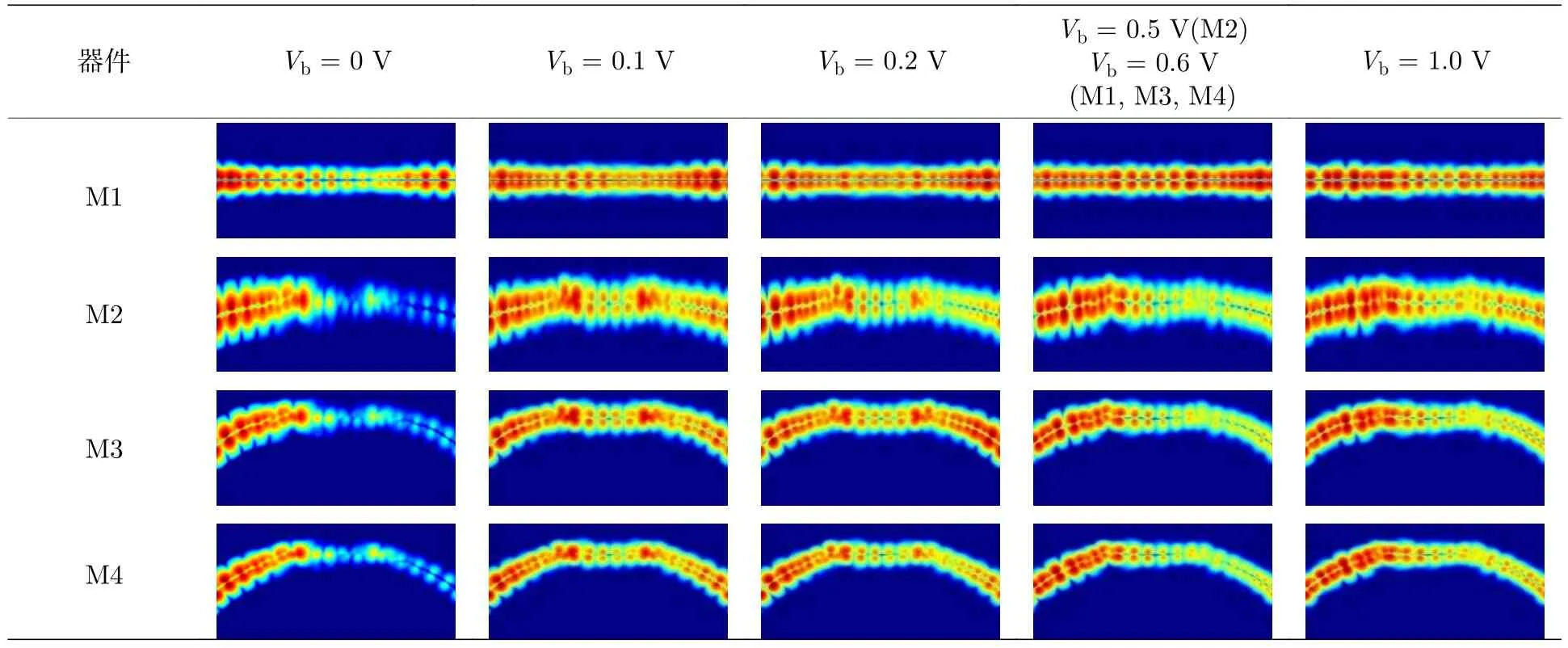
表3 器件M1—M4 在零偏压、+0.1 V,+0.2 V,+0.6 V 和+1.0 V 下散射态实空间分布图,色坐标参考图5(b)Table 3.Real-space scattering state distribution of devices M1−M4 under zero bias,+0.1 V,+0.2 V,+0.6 V and +1.0 V,all the figures share the same color bar given in Fig.5(b).

4 结论

本文采用非平衡格林函数(NEGF)结合密度泛函理论(DFT)探讨了锯齿型石墨烯纳米带(ZGNR)电极弯折对2-苯基吡啶分子器件负微分电阻特性的调控机理.由I-V特性及透射谱随偏压的变化说明,器件具有NDR 特性,且ZGNR 电极弯折能够调控NDR 特性,提升器件的负阻性能.分析认为,ZGNR 电极弯折后器件的2-苯基吡啶分子与ZGNR 电极间耦合减弱,弱耦合条件下,外加偏压后器件的透射系数因能级的移动和偏压的变化而产生大幅波动,故器件M2—M4 在外加低偏置电压(0.1 V 或0.2 V)处即出现大的透射系数,产生峰值电流Ip,降低了器件的Vp值,且增大了PVR 值,NDR 对应的电压区间向低偏压方向移动.平衡态下器件M1—M4 的透射谱、态密度和散射态实空间分布图解释了ZGNR 电极弯折后器件的中心分子与电极间的耦合减弱,由投影态密度计算结果解释了二者间耦合减弱是源于ZGNR 电极弯折.电极弯折改变了中心分子与电极间电子的相互作用,使两者间的波函数交叠发生变化是器件中心2-苯基吡啶分子与ZGNR 电极间耦合减弱的主因.因此,分子器件的电子输运性质不仅取决于中心分子和电极的固有特性,两者间耦合强弱的变化对其输运特性也产生显著影响.本文中高对称结构的分子器件,通过控制电极弯折角度能够调控中心分子与电极间耦合的强弱进而影响了器件的输运特性.ZGNR 电极弯折后,器件M2—M4 的NDR均较M1 表现出Vp减小,PVR 增大,其中电极弯折角度为15°时,器件M2 的PVR 值最大为12.84,Vp值减小至0.1 V,其所获得的低Vp、高PVR 的负阻特性在低功耗分子电子领域具有潜在的应用前景.

综上所述,本文中采用基础吡啶分子构建的器件模型结构简单,利用了石墨烯材料的优良特性,如引言中所述“控制石墨烯形变状态可调控其输运特性”,通过弯折ZGNR 电极调控器件中心分子与电极间的耦合,使器件表现出实际应用中希望的低Vp、高PVR 的NDR 特性,为实现实验制备提供可能.

本文工作由鸿之微提供计算机时支持.