改进粒子群算法在光伏MPPT中的应用

迟耀丹，陈 兵，徐红伟，赵 阳，李 腾

(1.吉林建筑大学寒地建筑综合节能教育部重点实验室，吉林长春 130118；2.四平市巨元瀚洋板式换热器有限公司，吉林四平 136100)

由于各类生产设备以及家用电器的大量投入，全球对电能的需求量急剧增加。面对有限的化石燃料和无限增长的电能需求量，全球纷纷寻找可再生能源。太阳能凭借环保、低噪声和取之不尽用之不竭等优势，得到了全球的认可。当光伏阵列受到不均匀光照时，其P-V输出为多个局部极大值和一个最大值的多极值非线性曲线[1]，增大了最大功率点跟踪的难度。

MPPT 算法一直是人们关注的热门问题，其中传统的方法有：扰动观测法[2]、电导增量法[3]等。但是上述传统的MPPT 算法存在容易陷入局部功率极大值的缺点。近年来人们将智能控制算法应用到MPPT 算法中，取得了一定的突破。文献[4]将模糊控制应用到了光伏MPPT 技术中，在功率跟踪时间和精度上取得了一定的进展，但模糊控制要依赖专家经验，实用性较差。文献[5]提出了一种基于PSO 算法的MPPT技术，有效提高了最大功率点跟踪的速度和精度。由于PSO算法本身存在容易陷入局部最优解的缺陷，所以该MPPT 技术并没有解决光伏发电系统容易陷入局部功率极大值的问题。文献[6]中将BP 神经网络与PSO 算法相结合，取得了较为理想的跟踪效果，但是神经网络算法需要获取大量的数据和进行复杂的学习训练，实现较为困难。

综上，在现有的光伏MPPT 算法中，都具有一定的不足之处，所以光伏MPPT 算法还需要进一步的探索。本文通过对PSO 算法二次开发，提出了一种NPSO 算法。该算法把种群粒子分为两类：收敛粒子和自由粒子，增强了PSO 算法的全局搜索能力。将NPSO 算法应用到光伏MPPT 中，研究结果表明，本文提出的MPPT 算法能够大幅度的提升功率跟踪成功率和发电效率。

1 光伏发电系统及光伏阵列输出特性

1.1 光伏发电系统模型

图1 为光伏发电系统框图。由图1 可知，光伏发电系统主要由光伏阵列、Boost 升压电路、逆变器和MPPT 算法等组成。

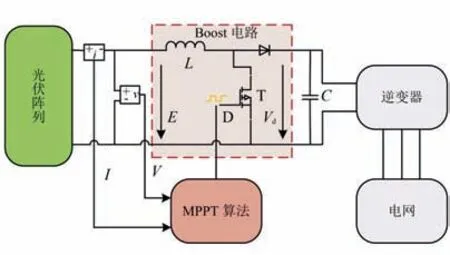
图1 光伏发电系统框图

Boost 升压电路的输出电压Vd的表达式为：

式中：V为光伏阵列的输出电压；D为输入开关管T 的PWM波形的占空比。

1.2 光伏阵列输出特性

本文以SIEMENS SP75 光伏组件为例，在Simulink 环境下，搭建起由3 块光伏电池板串联的光伏阵列模型。为了研究在不同程度下不均匀光照时的P-V输出特性曲线，本文设计了三种光照模式。光照模式1 为三块光伏电池受到的光照强度均为1 000 W/m2；光照模式2 为三块光伏组件受到的光照强度分别为1 000、1 000 和500 W/m2；光照模式3 为三块光伏组件受到的光照强度分别为1 000、300 和800 W/m2[7]。单块SIEMENS SP75 光伏组件的参数如表1 所示。光伏阵列在三种光照模式下的P-V输出特性曲线如图2 所示。

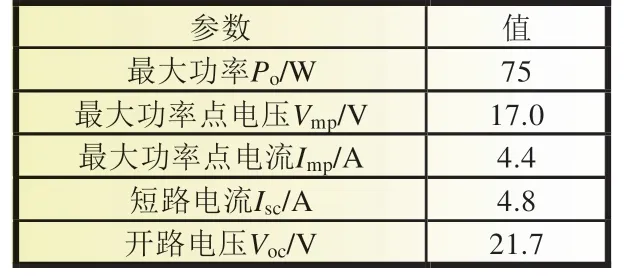
表1 SIEMENS SP75 参数

图2 光伏阵列P-V输出特性曲线

由图2 可知，在光照模式1 下，光伏阵列的P-V输出特性曲线是一条单峰值、开口向下的曲线。最大功率点处的电压和功率分别为51.0 V 和224.4 W；在光照模式2 下，光伏阵列的P-V输出特性曲线是一条具有两个峰值、开口向下的曲线。最大功率点处的电压和功率分别为33.1 V 和156.5 W；在光照模式3 下，光伏阵列的P-V输出特性曲线是一条具有三个峰值、开口向下的曲线。最大功率点处的电压和功率分别为34.33 V 和125 W。由图2 还可看出，随着光伏阵列局部阴影遮挡程度的增加，光伏阵列P-V输出特性曲线的峰值数量会向增多的趋势发展。

2 改进PSO 算法在光伏MPPT 中的应用

2.1 原始PSO 算法

式中：k为粒子更新的代数；为种群中第i个粒子在第k代的位置为种群中第i个粒子在第k-1 代的位置；为种群中第i个粒子在第k代的速度，i=1,2,3,...,N，N为种群中粒子的总数；xpbesti为第i个粒子的个体最优解；xgbest为整个种群的全局最优解；ω 为惯性权重因子；r为介于0 和1 之间的随机数；c1和c2为学习因子。

2.2 改进PSO 算法

本文通过在原PSO 算法上进一步改进，提出了一种NPSO算法。该算法把种群粒子分为两类：收敛粒子和自由粒子，其中自由粒子为两个。收敛粒子与原始PSO 算法中的粒子性质一致，具有速度和位置，在每次迭代时按照式(2)和式(3)进行更新。自由粒子只有一个参数：位置，且自由粒子不具有记忆性，在规定的搜索空间内随机取值。若自由粒子搜索到解，也即自由粒子的位置，优于当前的全局最优解xgbest，自由粒子就会把其位置分享给收敛粒子，把全局最优解更新为此时自由粒子搜索到的解，即令xgbest=当NPSO 算法中的收敛粒子陷入局部最优解，失去全局搜索能力时，自由粒子仍然在全局搜索空间内进行搜索。

自由粒子的搜索过程分为两个阶段，第一阶段为种群粒子迭代次数在gen代之内。此阶段，自由粒子在全局搜索空间内搜索。记全局搜索空间为[xmin,xmax]，并令自由粒子1 的搜索区间为[(xmax-xmin)/2,xmax]，自由粒子2 的搜索区间为[xmin,(xmax-xmin)/2]。自由粒子的作用是增强全局搜索能力，避免陷入局部最优解。

第二阶段是种群粒子迭代次数在gen代之后，此阶段，自由粒子不再进行全局搜索，而是以全局最优解xgbest为中心，rad为半径进行微小区域的随机搜索。此阶段，自由粒子的作用是使当前种群粒子能够更加细致地搜索全局最优解，提高搜索的精度，并能够加快收敛粒子的收敛速度。记两个自由粒子的位置分别为和。和的表达式分别为：

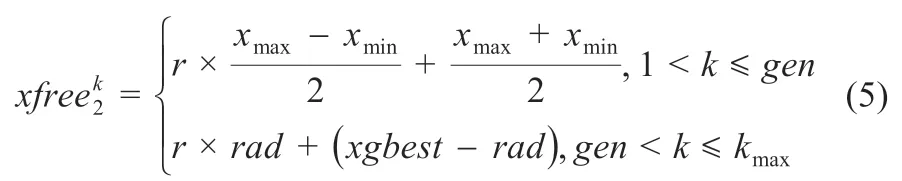
式中：r为区间[0,1]内的随机数；k为粒子迭代代数；kmax为种群最大迭代次数；rad为自由粒子在第二阶段的搜索半径。rad的表达式为：

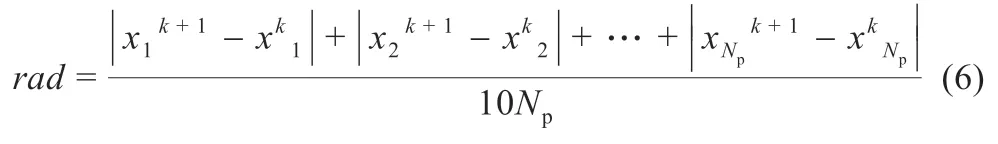
式中：Np为收敛粒子的个数。

2.3 NPSO 算法在光伏MPPT 中的应用

自由粒子1 和自由粒子2 位置的计算式分别为：

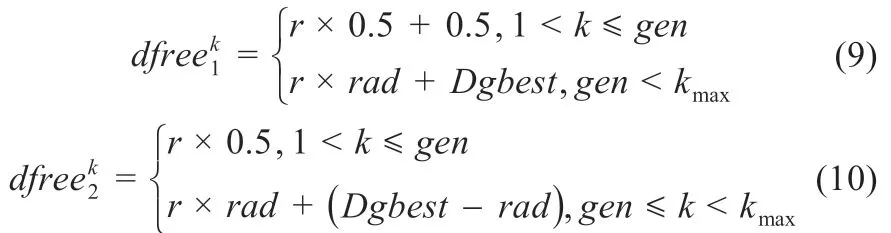
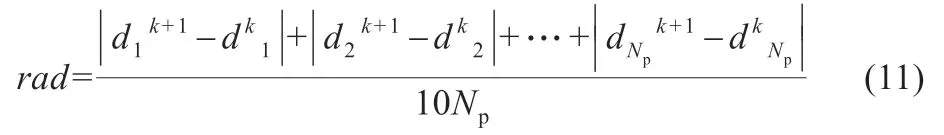
种群粒子的目标函数的表达式如式(12)所示：

式中：Ppv为光伏阵列输出功率；Vpv为光伏阵列实时输出的电压值；Ipv为光伏阵列实时输出的电流值。

NPSO_MPPT 算法的具体执行步骤如下：

步骤1：初始化粒子种群；

步骤2：获取光伏阵列的实时输出电压Vpv和实时输出电流Ipv，并计算第i个收敛粒子在第k代的适应值和第i′个自由粒子在第k代的适应值

步骤4：更新收敛粒子的速度和位置以及两个自由粒子的位置；

步骤5：判断k是否满足k＞kmax，如是，则结束迭代，执行步骤6，否则令k加1 并返回步骤2 继续迭代；

步骤6：判断当前外部环境是否发生变化，若当前外部环境没有发生变化，则输出全局最优解Dgbest，否则返回步骤1。

NPSO_MPPT 算法的程序流程图如图3 所示。

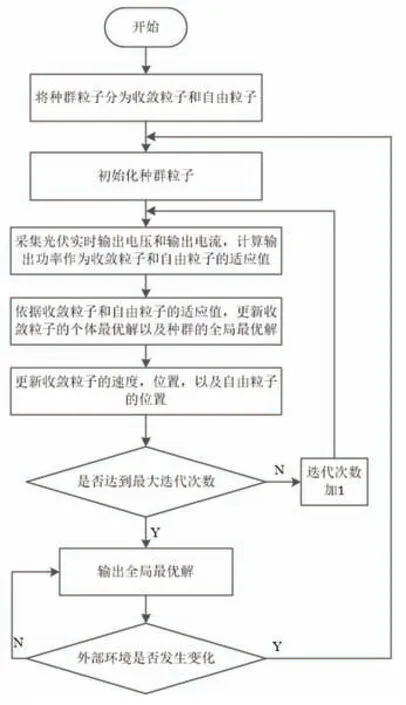
图3 NPSO_MPPT算法的程序流程图

3 效果验证

为了对基于NPSO 算法的MPPT 算法进行验证，在Simulink 环境下搭建起基于Boost 电路的仿真模型如图4 所示。在图4 中，PV array 为三块SIEMENS SP75 光伏组件串联的光伏阵列，C1=10µF，L1=1.5 mH，C2=50µF，R1=53 Ω。

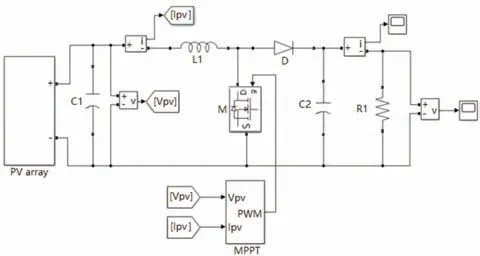
图4 基于Boost升压电路的光伏系统仿真模型

在上述三种光照模式下，分别对P&O、PSO_MPPT 算法和NPSO_MPPT 算法进行了50 次实验测试。每次实验时P&O 的初始输出占空比在区间[0,1]内随机取值。PSO 和NPSO 算法的粒子数量均为6 个，最大迭代次数为20 次，NPSO 算法的参数gen值为8。

图5 为在光照模式3 下的P&O、PSO_MPPT 算法和NPSO_MPPT 算法的仿真结果图。

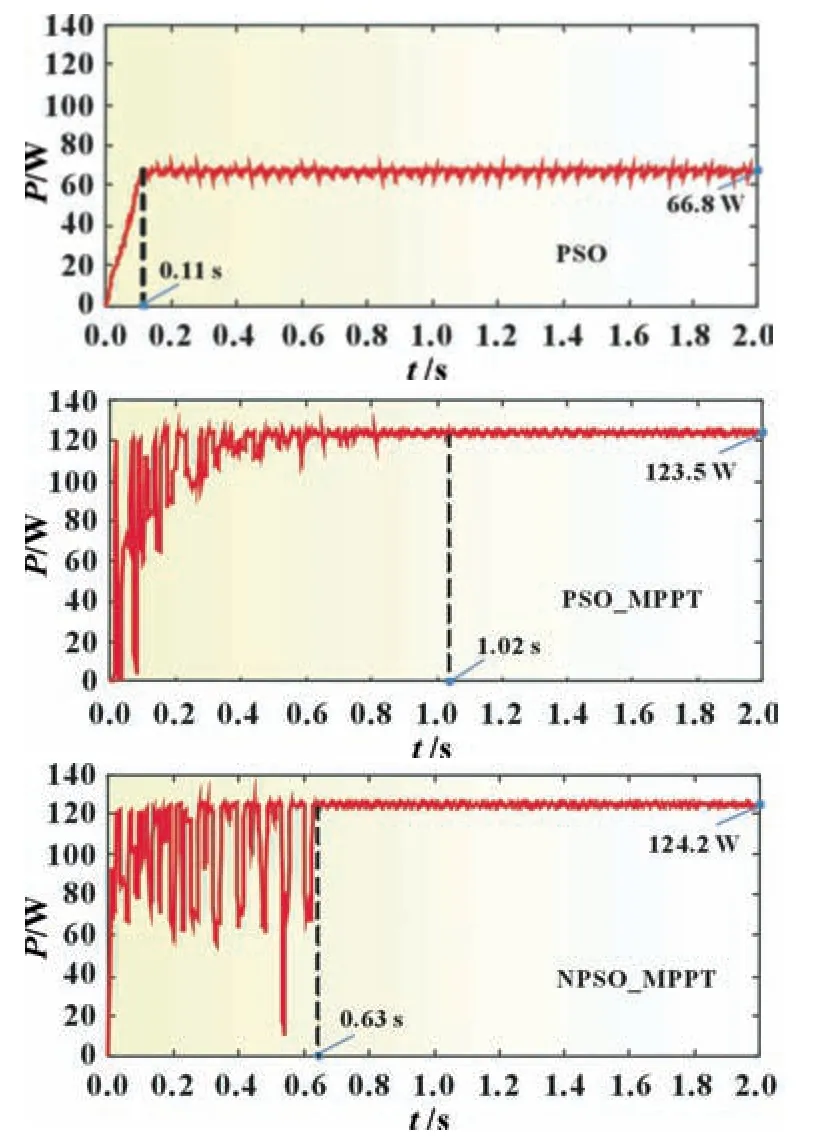
图5 光照模式3下的仿真结果

由图5 可知，在光照模式3 下，即光伏阵列的P-V输出曲线为三个峰值的条件下，P&O 算法在0.11 s 时，光伏阵列的输出功率波形趋于稳定，最终在2 s 处跟踪到了功率66.8 W。结合图2 可知，此功率为光伏阵列输出功率的局部极大值功率，发电效率为53.44%。PSO_MPPT 算法在1.02 s 时，光伏阵列的输出功率波形趋于稳定，最终在2 s 处跟踪到了功率123.5 W，发电效率为98.8%。NPSO_MPPT 算法在0.63 s 时，光伏阵列的输出功率波形趋于稳定，最终在2 s 处跟踪到了功率124.2 W，发电效率为99.36%。

表2为P&O、PSO_MPPT算法和NPSO_MPPT算法分别在光照模式1、光照模式2和光照模式3下的实验数据统计表。

表2 仿真数据统计表

由表2 可以看出，P&O 算法在光照模式1、光照模式2 和光照模式3 条件下的功率跟踪成功率分别为：100%、76%和42%。由此可知，P&O 算法不适合应用在局部阴影遮挡条件下的光伏发电系统中；PSO_MPPT 算法在光照模式1、光照模式2 和光照模式3 下的功率跟踪成功率分别为100%、92%和90%。由此可知，PSO_MPPT 算法仍然存在陷入局部功率极大值的问题；NPSO_MPPT 算法在三种模式下的功率跟踪成功率均为100%，解决光伏发电系统在局部阴影条件下容易陷入局部功率极大值的问题，有效提高了光伏发电的效率。

通过分析PSO_MPPT 算法的仿真结果发现，陷入功率局部极大值的多数情况是因为种群粒子初始化时，多数粒子位置分布在了局部功率极大值附近。为了进一步验证NPSO MPPT 算法跳出局部功率极大值的性能。在光照模式3 下，特地在局部功率极大值附近选取了一组数据作为粒子初始化时的位置，分别为0.05、0.35、0.25、0.12、0.40、0.36，并分别对PSO_MPPT 算法和NPSO_MPPT 算法进行了50 次测试。

仿真结果统计如表3 所示。由表3 可以看出，基于NPSO算法的MPPT 技术成功跟踪到功率最大值的概率为84%，而基于PSO算法的MPPT技术均跟踪到了局部功率极大值，并无法跳出。

表3 实验数据统计表

图6 为PSO_MPPT 和NPSO_MPPT 算法的仿真结果。由图6 可知，PSO_MPPT 算法陷入了局部功率极大值，最终收敛到了功率78.6 W 处。NPSO_MPPT 算法在0.26 s 之前，收敛粒子逐步陷入了局部功率极大值。在0.26 s时，自由粒子搜索到了优于当前全局最优解的解，逐渐促使收敛粒子跳出了局部功率极大值。最终粒子全部收敛在了功率最大值124.2 W 处。

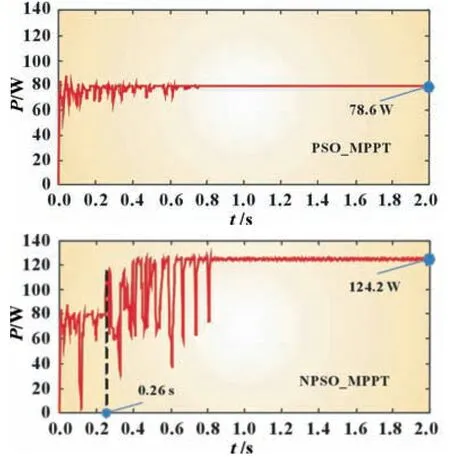
图6 PSO_MPPT和NPSO_MPPT算法的仿真结果

4 结论

本文通过对PSO 算法的改进，提出了一种NPSO 算法，弥补了PSO 算法容易陷入局部最优解的缺陷，增强了PSO 算法处理多峰值问题的性能，并将NPSO 算法应用到光伏MPPT中。实验结果表明，本文提出的NPSO_MPPT 算法与现有的P&O 和PSO_MPPT 算法相比不仅跟踪成功率有了大幅度的提升，而且提高了光伏发电效率。