储能改进型Y源光伏逆变器的滑模控制策略

孟令鹏，希望·阿不都瓦依提，吕海鹏，石存金

(新疆大学电气工程学院，新疆乌鲁木齐 830047)

随着“碳达峰、碳中和”目标的提出，我国能源的消费结构将发生深刻变化，各类清洁能源将得到大力发展，而太阳能作为一种清洁、高效、易获取的能源得到人们的广泛青睐。光伏逆变器是光伏发电系统中的关键部分，传统光伏逆变器普遍采用两级式拓扑结构，存在成本高，效率低等问题[1]。为解决上述问题，彭方正团队提出了Z 源逆变器(Z-source inverter,ZSI)，在单级变换器中实现升降压和逆变功能，且不受直通的影响，提高了系统的可靠性[2]，被广泛应用于光伏系统中。然而，ZSI 存在电流不连续、升压比较低、元器件应力较大等不足，相关学者又提出了qZSI、Trans-ZSI、Γ-ZSI 等改进型阻抗源逆变器[3-6]。其中，改进型Y 源逆变器(improved Ysource inverter,IYSI)升压比高，电流连续，同时具有灵活的绕组匹配度，可以获得不同的升压比，是近年来的研究热点[7]。

由于光伏系统固有的间歇性和随机性，使输出功率呈现波动性，并限制光伏系统的适用性[8]，因此，通常在光伏发电侧增加储能系统，以此来降低系统的波动性和存储多余能量。而大部分储能系统采用双向DC/DC 变换器来控制蓄电池的充放电，增加了系统的复杂度和控制难度，降低了系统效率。鉴于此，文献[9]提出储能型准Z 源逆变器(energystored quasi-Z-source inverter,ES-qZSI)，将蓄电池组直接并联在Z 源网络的一个电容上，实现对蓄电池的充放电控制，而无需任何额外的DC-DC 电路，因此该拓扑具有结构简洁，成本低的特点[10]。然而，传统的ES-qZSI 系统存在升压比低的问题，且对前级光伏板和蓄电池电压有较高的需求。为解决上述问题，文献[11]将蓄电池并联在IYSI 的电容C1上，可以提高电压增益，降低对蓄电池和光伏板的电压要求，同时通过控制直通占空比D和调制比M两个控制自由度就可以实现光伏MPPT、蓄电池组充放电以及交流侧输出功率。然而，ES-IYSI 是一个五阶非线性系统，其传递函数具有非最小相位零点，且无法通过调整电路的参数加以消除，当输入电压发生扰动的时候，这个不稳定零点会造成直流侧电压的超调和振荡，这增加了控制器的设计难度。

目前，针对IYSI/ES-IYSI 的控制策略普遍采用电压外环、电流内环的双环PI 控制方法，但PI 控制参数调整困难，同时应用于非线性系统时控制效果不佳。因此，针对IYSI 这类非线性阻抗网络逆变器，有文献提出了一些非线性控制方法。文献[12]将模糊控制应用于ES-qZSI，提高了电网电流质量，降低了电池充放电脉动，但模糊控制器的设计缺乏系统性，参数选择过于依赖经验。文献[13]将能量成型控制方法(PHC)应用到IYSI 中，简化了控制器的设计，使控制速度更快，但并没有研究参数变化对输出电压和全局稳定性的影响。在精细化建模方面，文献[14]为降低ES-qZSI 系统的二倍频波动，建立了详细的数学模型，提出了系统参数的相关设计方法。文献[15]用小信号模型法推导出qZSI 的传递函数，基于传递函数设计了直通控制器。然而，到目前为止，针对ES-IYSI 的详细建模及SMC 的研究，相关文献、成果较少，研究亟待深入。

本文采用滑模控制方法对ES-IYSI 的直流侧和交流侧分别控制，首先分析了ES-IYSI 工作原理及工作模式，然后用状态空间法推导了系统的数学模型，同时用小信号模型进行暂态分析，在此基础上给出了滑模控制的设计方法和步骤。最后通过仿真验证了双滑模控制的有效性。

1 ES-IYSI 系统结构与数学模型

单相ES-IYSI 系统结构如图1 所示。它由改进型Y 源网络、电池模组和逆变器组成。改进型Y 源网络包括三绕组耦合电感、两个电感L和Lb、两个电容C1和C2和一个二极管D。电池模组可以简化为开路电压VSOC和内阻Rb的等效模型。

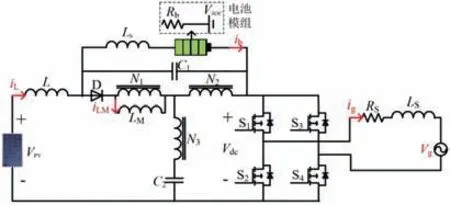
图1 单相ES-IYSI系统的结构

1.1 功率流动

如图1 所示，ES-IYSI 需要控制三端功率：光伏板输入MPPT、蓄电池储能SOC以及输出功率。通过控制两个功率流，第三个功率流自动补足功率差，如式(1)所示[16]：

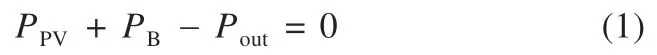
式中：PPV为光伏功率，始终为正；PB为电池功率，吸收功率时为负，释放功率时为正；Pout为逆变器输出功率，始终为正。

从式(1)可以看出，控制三种功率流的方式有三种：(1)控制光伏板的输出和并网功率，蓄电池的充放电功率可以根据式(1)自动匹配；(2)控制并网和蓄电池功率，光伏功率可以根据式(1)自动匹配；(3)控制光伏板的输出和蓄电池的充放电功率，并网功率可以根据式(1)自动匹配。本文采用第一种控制方法。

1.2 ES-IYSI系统建模

ES-IYSI 与ZSI 类似，有两种变换状态：任意支路上的上下两个开关器件同时导通时，即可进入直通状态如图2(a)所示，二极管D 反向截止，逆变器输出功率为零；图2(b)为非直通状态，逆变器向电网输送功率，二极管D 导通。

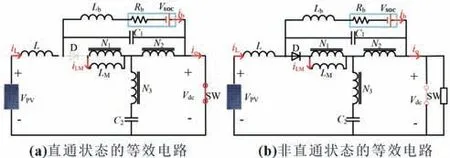
图2 单相ES-IYSI系统的工作模式

由图2(a)可得系统直通状态下的状态空间方程：

式中：α1=N1/(N2-N3)；F=diag(L,C1,LM,C2,Lb)；X=[iL,VC1,iLM,VC2,ib]T；u=[VPV,Vdc,VSOC,io]T。

由图2(b)可得系统非直通状态下的状态空间方程：

式中：α2=N1/(N1+N2)；α3=(N1+N3)/(N1+N2)；α4=(N3-N2)/(N2+N3)。

考虑电力电子变换器动态建模中的状态空间平均技术，在开关频率足够高的情况下，可将式(2)和式(3)结合起来，得到系统的平均状态方程为：

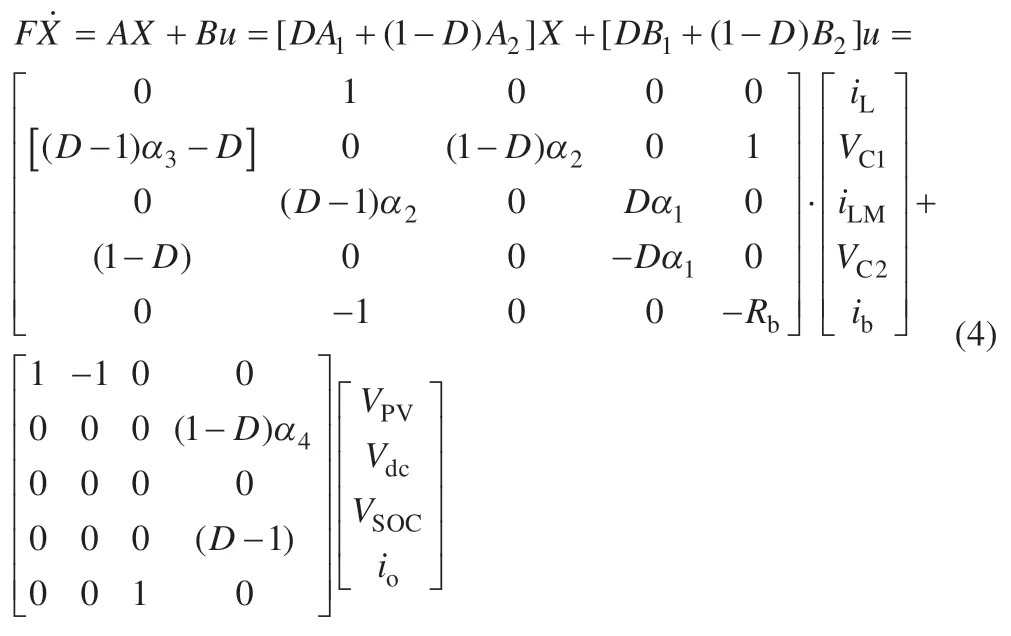
式中：D为直通占空比，它是一个周期内系统直通状态时间与开关周期的比值。

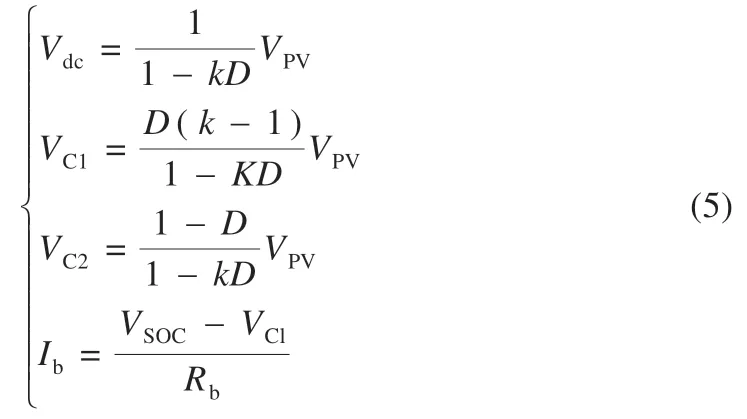
式中：k=1+[(1+N12)/(1-N32)]。

式中：k1=(α3-1)iL-α2iLM-α4io；k2=α2VC1+α1VC2；k3=-iL-α1iLM+io。

对式(7)进行拉普拉斯变换可以得：

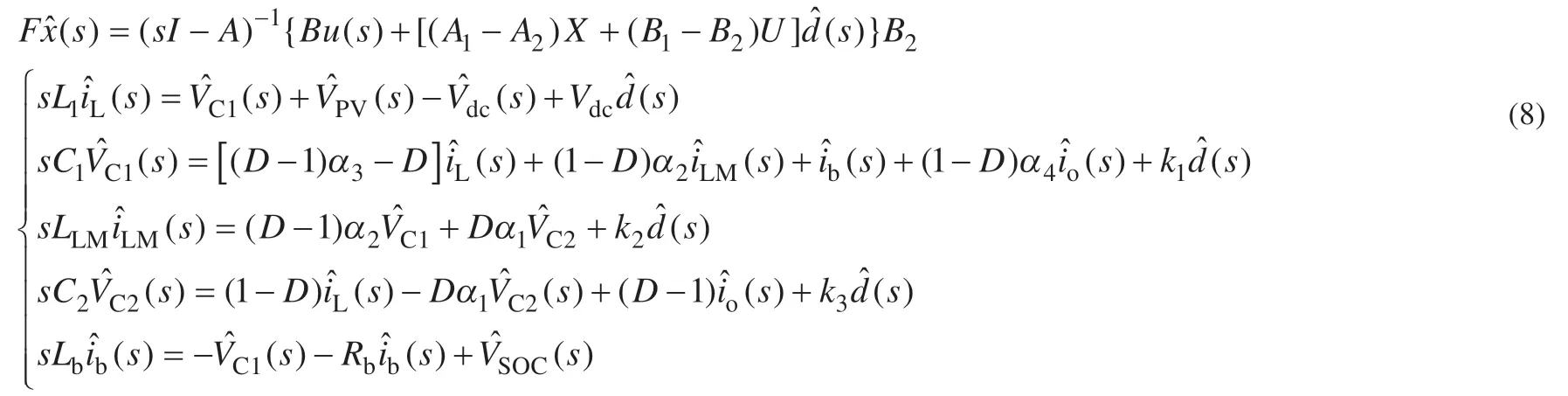
根据式(8)，运用梅逊增益公式可以计算ES-IYSI 直通占空比到电池电流的开环小信号传递函数如式(9)所示：

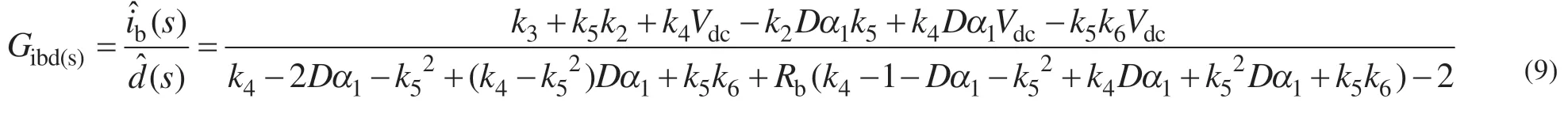
式中：k4=[(D-1)α3-D]；k5=(1-D)α2；k6=Dα1(1-D)。

根据式(9)可知该系统存在右半平面零点，这会导致系统的振荡和非最小相位响应。

2 ES-IYSI 滑模控制器设计

2.1 直流侧滑模控制

考虑直流电容电压的非最小相位特性，直接控制占空比来控制电容电压容易造成响应滞后，性能达不到要求，因此采用电流间接控制的方式，为设计直流侧SMC，系统的状态变量误差可定义为：

该控制器的滑模面为以上状态变量的线性组合，表示为：

式中：β1、β2为滑模控制器增益。

当系统各变量运动到滑模面时，各变量都将追踪设定值，上述选取的滑模函数S=0，将式(14)对时间常数求导，并将式(12)和(13)代入式(14)可得：

为了增强系统的鲁棒性，控制率被设为：

式中：Dsh是一个连续变量，通常介于0 到1 之间，但在ES-YSI中升压比为1/(1-KD)，因此Dsh的值域为[0,1/K]。

2.1.1 存在条件

当运动到滑模面时，状态轨迹必须限制在滑模面上，并向零点移动，因此令系统的李雅普诺夫函数及其导数为：

为保证滑模运动的存在，必须满足局部可达条件，如式(19)所示：

将式(14)和(15)代入式(19)，由此得到不等式(20)：

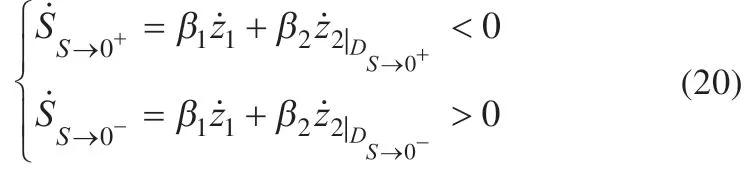
式(20)为ES-IYSI 系统滑模运动的存在条件，可将其分为以下两种情况：

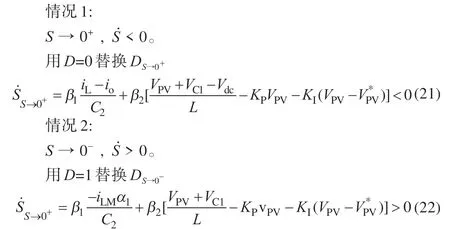
将储能改进型Y 源逆变器参数代入上述不等式进行验证，滑模控制的系数由以上不等式计算得出。

2.1.2 稳定性条件

用等效控制Dsh替代ES-IYSI 的大信号平均模型，将不连续系统转化为理想的滑模连续系统，如式(23)：

2.2 交流侧滑模控制

为了控制ES-IYSI 输出的电能质量，必须控制逆变器的输出交流电流，本文设计了一套SMC 来控制交流侧的输出。

选取滑模面的函数为：

由图1 可知交流侧的状态方程为：

将式(25)代入式(24)可得：

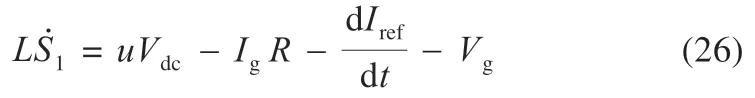
选择趋近律公式为：

式中：K1、K2为滑模控制系数。

结合式(26)与(27)，并令=0，解得等效控制率Ueq：

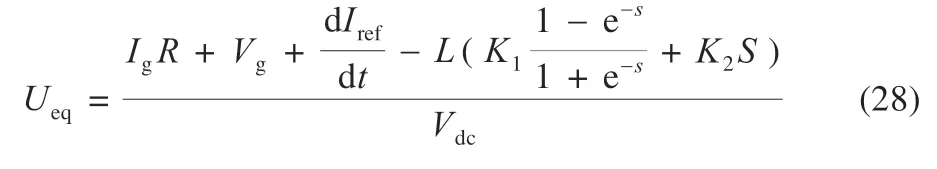
式中：Ueq实际是调制比M，用以控制并网电流。

详细控制策略如图3 所示，通过直流侧滑模控制得到调制信号Dsh，通过交流侧滑模控制得到调制信号M，调制信号M 和D 组合在一起产生控制逆变器的SPWM 信号，用来实现三端功率控制。

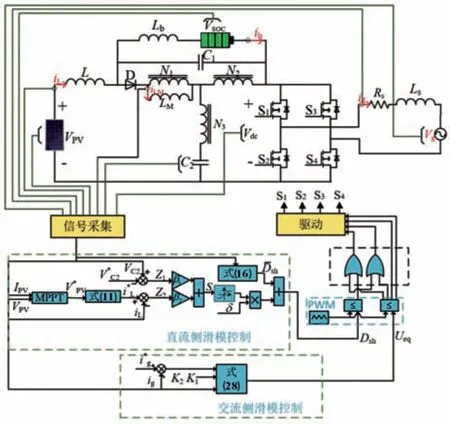
图3 滑模控制详细框图

3 仿真验证

为了验证双滑模控制策略的正确性，利用Simulink 仿真软件搭建系统的仿真模型。对图3 进行仿真分析研究，系统仿真参数见表1，仿真中光伏模块选用Kyocera KD135Gx，光伏板的数据见表2，采用8 串6 并组成一组光伏系统，储能电池为一个200 V/100 Ah 的锂电池系统。

表1 ES-IYSI 系统仿真参数

表2 光照1 000 W/m2,温度25 ℃时光伏板参数

3.1 光伏最大功率跟踪

图4 为仿真选用的光伏板P-V和I-V特性曲线，当太阳辐射发生变换的时候，曲线也不同，造成最大功率点的不同，为了保证光伏板的输出时刻处于最大功率点，本文采用扰动法跟踪最大功率点。

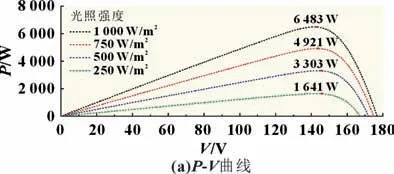
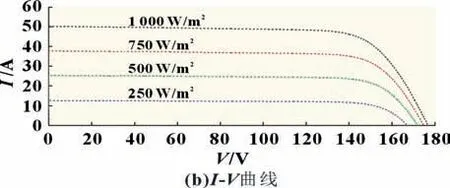
图4 温度25 ℃不同光照强度下的光伏板的P-V/I-V特性曲线

3.2 功率波动

蓄电池组可以在系统中起到削峰填谷的功能，图5 可验证该功能。图5 为ES-IYSI 在双SMC 控制下的工作波形。如图5(a)所示，开始时，光伏板输出功率大于交流侧输出功率，蓄电池开始充电；0.3 s 时光伏输出功率降低到4 000 W，交流侧输出功率维持4 000 W 不变，光伏板发出功率与交流侧功率相等，蓄电池组既不充电也不放电；0.5 s 时光照强度保持不变，交流侧输出功率上升到5 500 W，交流侧输出功率大于光伏板发出的功率，蓄电池组开始放电补足功率差额；图5(b)为蓄电池充放电情况，当光照强度或并网功率发生变化时，电池电流可以精准跟踪这种变化，补足功率差额；图5(c)为并网电流，当光照强度发生波动时，并网电流经过0.03 s 波动后迅速调整到稳态值，当输出功率增大时，并网电流随之增大，经过0.05 s 后趋于稳定。仿真验证了当功率波动时，ES-IYSI可以维持三端功率平衡，通过改变电池的充放电功率，进而保证并网功率的平稳。

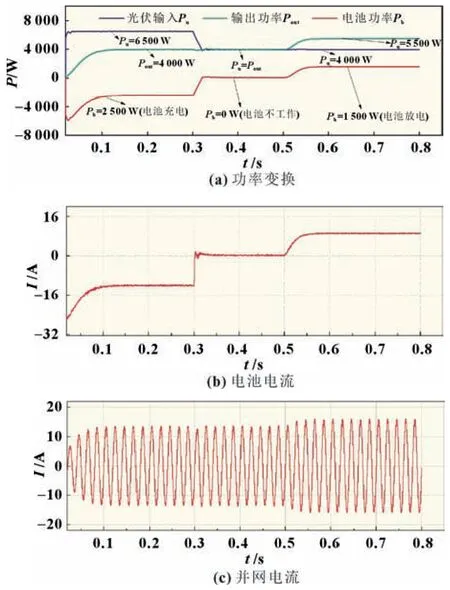
图5 ES-IYSI光伏输出和功率输出变换时波形

3.3 动态性能

图6 为光照强度突变时，采用PI 控制以及SMC 控制下的电池和并网电流波形图。由图6(a)、(b)可知，采用SMC 控制电池电流的响应速度快，超调量小,可快速补足功率差额，由此说明，SMC 的大信号性质在一定范围内具有更强的鲁棒性；图6(c)、(d)为两种控制方式下的并网电流波形，在本文方法下，并网电流的谐波含量(THD)为2.75%，传统PI 控制策略下，THD为4.22%，SMC 控制下并网电流动态响应速度及畸变率均优于PI 控制，提高了并网电能质量。

图6 光照强度突变时的动态波形

4 结论

本文采用滑模控制方法对ES-IYSI 系统的动态响应进行控制，首先对ES-IYSI 进行精细化建模，进而建立了系统的数学模型，然后设计了直流侧和交流侧的SMC，实现了对光伏输出、储能电池组和交流输出的三端功率控制，通过仿真验证了双滑模控制策略在ES-IYSI 系统的有效性。与双环PI 控制相比，本文所提策略提高了系统的稳定性，而且缩短了系统的稳态响应时间，降低了谐波含量。本文提出的控制策略可以简化控制器的设计，针对高阶非线性系统以及输入波动强的场景控制效果较好，具有一定的实用价值。