基于强化学习的干线信号混合协同优化方法

马东方，陈曦，吴晓东，金盛*

(1.浙江大学，海洋传感与网络研究所，杭州 310058；2.公安部，交通管理科学研究所，江苏无锡 214151)

0 引言

城市化进程的快速发展和小汽车保有量的持续增加对城市交通管理与控制不断提出新的挑战，交通拥堵已经成为诸多城市普遍存在的严峻问题。为缓解交通拥堵，保障路网交通流畅通，研究者从需求引导、交通组织及信号控制等多个角度进行系统化探索，提出了诸多行之有效的措施和方法。信号控制是在给定的路网结构和交通组织方案下，通过信号灯调节分配冲突交通流的通行权，实现网络时空资源的优化配置，提高路网交通流的整体运行效率。目前，关于信号控制的优化已有很多研究成果，按其优化手段可分为模型驱动和数据驱动两类。模型驱动通常以排队最短、延误最小及停车次数最少为优化目标，以交通流量为输入变量，通过理论推导刻画目标函数的显式数学表达模型。然而，上述理论推导过程往往伴随很多理想化假设(例如，规律性的车辆到达模式等)，与实际交通流运行状态存在较大偏差，致使该类方法的实际控制效果欠佳。数据驱动类方法多以强化学习为手段，通过决策行为与环境空间的动态交互探究交通流运行状态的各种深层次和非线性特征，刻画各类复杂运行状态和信号方案下的交通流运行效果，提升决策方案的实施效果，是信号优化的新兴趋势。

与模型驱动类方法单纯以流量数据为因变量不同，强化学习类方法的基础输入为状态空间，即由实际交通流数据提取的排队长度和延误时间等信息组成的向量或矩阵表达。信号控制的状态空间属性一般为连续变量，使用传统的表格式强化学习面临着高维状态存储困难和搜索耗时巨大等难题。为此，很多学者将深度学习的感知能力与强化学习的决策能力相结合，设计了一些基于深度强化学习的信号优化方法。例如，LI 等[1]提出了一种基于深度Q学习网络(Deep Q-learning network,DQN)的信号控制方案优化方法，并验证了该网络具有很好的性能。亦有学者基于其他深度强化学习算法构建了多类新型信号控制优化方法，例如，Actor-Critic(AC)方法等[2]。然而，现有研究主要侧重于算法的模型设计，忽略了对状态空间的精化。近年来，越来越多的数据被纳入状态空间，例如，等待时间、通行时间及承载车辆数等[3]；然而，状态空间的冗余信息不仅会增加模型训练的时间开销，也会制约算法的拟合优度，降低方案性能[4]。因此，智能体状态空间优化是一项非常必要且重要的工作。

多路口交通流之间存在密切时空相关性，其信号方案之间亦存在交互影响，应通过协同控制的方式确保多路口方案的整体最优性。多路口的协调控制策略主要分为集中式和分布式两类。集中式是将所有智能体的决策行为联合建模并统一优化，存在两点困境：一是算法复杂度随智能体数目的增加而爆炸式增长，无法应用于大规模区域；二是可扩展性受限，无法进行模型移植。分布式策略是融合本路口和邻接路口的交通状态与信号状态更新单智能体的状态空间[5]，并采用独立优化的方式实现多智能体协同，例如，Multi-Agent Actor Critic(MA2C)等[6]。然而，此类方法的智能体交互明显不足，无法保障全局最优性。

为提升智能体之间的信息交互，提高算法的实际控制效果，本文面向干线协调控制提出一种多智能体协同决策优化方法，设置中心和局部两类智能体：局部智能体基于DQN网络优化单路口方案；中心智能体评判局部智能体的学习策略，并从全局层面对局部智能体进行策略调整。为减少信息冗余，提升智能体学习效率和决策效果，本文首先优化单智能体的学习方式、状态空间及回报函数。

1 单智能体学习架构设计与优化

状态、回报及动作是强化学习的3 个基本要素。在信号优化中，强化学习的动作空间由相位相序结构直接决定，无需动态调整；状态和回报有多类表达形式，且这些表达形式直接决定了智能体的学习效果。因此，本文以单路口控制为基础阐述智能体架构设计及状态与回报的维度空间优化方法。

1.1 分布训练-分区记忆单智能体优化方法

强化学习的目标是最大化一个马尔可夫决策过程(Markov Decision Process,MDP)的长期回报。当决策问题的解空间相对较小时，可用表格描述状态与动作的价值函数(一般用Q 值表示)，进而以价值最大化为目标选择决策行为和生成动作方案；然而，信号优化的状态空间具有多样性和异构性，传统表格式强化学习方法无法枚举所有动作价值函数，利用深度学习拟合状态到决策的映射关系(即DQN 算法)成为近年研究的主流手段。基于DQN模型架构，本文设计了单智能体的深度网络，该网络包含3个子模块：特征提取、状态-回报映射关系挖掘及相位门控。特征提取模块利用卷积神经网络捕捉图像类信息的关键特征，并与数值类特性拼接为状态空间后输入至共享全连接层；全连接层挖掘交通状态与潜在回报的映射模式，并将映射模式与当前相位信息输入至相位门控模块；相位门控模块在模型训练阶段用以挖掘状态-Q值之间的映射关系[3]，在应用阶段是根据各个动作的Q 值和既定策略确定最佳动作。

信号优化中的当前相位信息至关重要。例如，某两相位控制路口，若当前时刻南北向放行，但东西向负荷大，则应切换相位；反之，保持当前相位。为突出当前相位信息的重要性，本文在相位门控模块设计如下学习策略：个体相位分布式训练决策模型，宏观决策时，利用当前相位对应的决策模型计算Q值并确定动作方案。

系统运行中，智能体与环境交互会产生多样化的相位-动作组合样本，每种组合的出现概率差异很大。若采用随机采样策略训练模型，则可能会出现低频率的相位-动作方案其样本量不足的风险，导致欠拟合现象。为此，本文设计一种分区记忆机制，即将不同相位-动作组合样本存储于独立记忆库，训练时，从多个记忆库中等量采集样本。单智能体优化网络如图1所示。

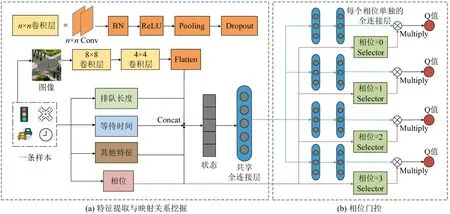
图1 单智能体优化网络Fig.1 Network forindividual agen

1.2 单智能体状态及回报优化

基于确定的单智能体决策优化模型，需进一步优化结构中的状态空间和回报函数。对于状态空间，首先，融合已有文献中的要素信息，组合多种待选状态空间，然后，基于效果测试确定最佳组合。同理，基于类似方式优化回报函数。

现有文献[4,5,8]中，常用的状态要素主要包含如下11项。

(1)进口道排队长度L。定义车辆速度小于0.1 m·s-1为排队等待状态。

(2)进口道承载车辆数Nin。承载车辆包含排队车辆和行驶车辆。

(3)出口道承载车辆数Nout。

(4)进口道延误D，计算方法为

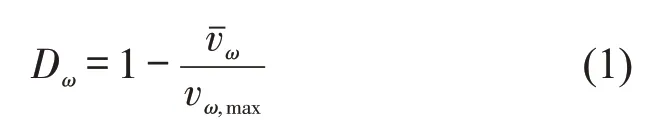
式中：Dω为进口道ω的车辆延误；和vω,max分别为ω的车辆平均速度和最大速度(m·s-1)。

(5)进口道车辆排队时间W，即进口道所有车辆的排队时间之和。车辆j在时刻t的等待时间为

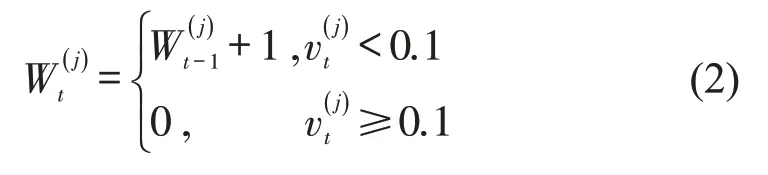
式中：为车辆j在时刻t的等待时间，即车辆速度小于0.1 m·s-1的累计时长(s)；为车辆j时刻t的速度(m·s-1)，车辆启动后其等待时间更新为0。

(6)车辆平均停车次数S，即车辆通过连续多个路口时的平均停车次数累计值。

(7)相位切换指示C。保持当前相位C=0；否则，C=1。

(8)实施动作a后Δt时段内通过路口的车辆数N。

(9)实施动作a后Δt时段内通过路口车辆的总通行时间T，即通过路口所有车辆在进口道的行程时间之和。

(10)路口图像信息M。将路口分割成大小相同的若干方形网格，个体网格能且仅能容纳单辆车辆。若网格被车辆占据则赋值为1；否则，赋值为0。基于路口图像信息的状态值表达示例如图2所示。

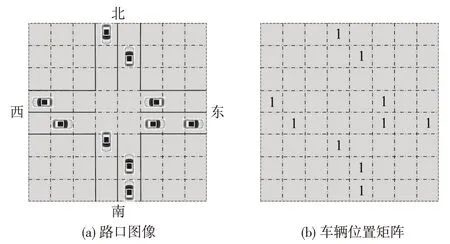
图2 路口的图像表示及车辆位置矩阵示例Fig.2 Image representation of an intersection and matrix of vehicle positions

图2(b)矩阵中的元素与图2(a)的网格一一对应，空缺元素表示单元网格内无车辆，信息值为0；容纳有车辆的矩阵元素信息值设置为1。

(11)路口当前相位Pc。

(12)路口下一相位Pn。

回报空间通常依据控制策略在状态空间中选择部分要素，进而通过权重分配确定回报函数的表达形式。以上状态指标1～6 均可作为回报函数的候选要素。假设回报函数包含x个要素，其函数模型可表示为

式中：rt,1为智能体独立运行时t时刻的回报值，即智能体的局部回报；Fχ为要素χ的回报值；αχ为权重系数。

由于干线协调的优化目标是在保障支路通行效率的基础上减少干线车辆的停车次数，因此干线平均停车次数应为关键回报要素，其函数构造方法将在第2部分详细讨论。

2 干线信号多智能体混合式协同控制

为平衡干线协调的全局最优性与算法复杂性，本文融合分布式和集中式两种协同策略优势提出一种混合式协同优化方法，该方法为每个信号路口配置1个局部智能体，并为这些局部智能体共同设置1 个全局智能体。局部智能体仅观测本路口状态，依据局部状态生成并执行本路口动作方案，进而输出当前回报；中心智能体观测全局状态，评价局部智能体与全局目标的一致性，并向局部智能体反馈附加回报，用以提升全局交通流运行效率。混合式协同的总体框架如图3所示，该架构通过智能体之间的交互合作最大化全局回报，同时，也保留了局部智能体的决策能力，降低了算法复杂度。

图3 多智能体干线协调控制框架Fig.3 Multi-agent cooperative optimization framework for arterial signals

2.1 中心智能体设计

回报函数应在单智能体状态空间的基础上融入全局要素，适当修正。从全局层面看，所有路段均同步兼有出口和入口属性，单智能体状态空间中的进口道承载车辆数在中心智能体中应调整为所有车道的承载车辆数。同时，为在支路交通流不受影响的前提下最小化主路车流的停车次数，关键回报指标应设置为干道停车次数。

本文将0.1 m·s-1的速度定义为排队状态的阈值，因此，车辆j在t时刻的停车次数为

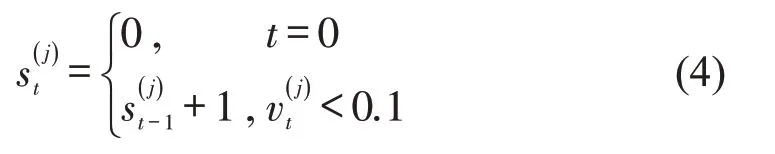
进口道ω在t时刻的平均停车次数St,ω为

式中：Jω为车道ω上的车辆数。

干线协调控制中，支路与主路具有差异化的重要性，中心智能体的回报函数应对干道和相交道路的要素设置不同的权重。假设智能体回报函数中包含x个要素，则干道和相交道路在t时刻的全局回报Rt,ψ为

式中：Ψ为符号变量，Ψ=1 代表相交道路，Ψ=2代表干道。

中心智能体的总回报Rt为

2.2 局部智能体设计

局部智能体的状态空间与传统单智能体设置方法保持一致，而回报包含局部回报和全局附加回报，即

式中：和分别为局部智能体n的局部回报和附加回报，n∈{1,2,3,…,K}。

当局部智能体的动作影响全局通行效率时，中心智能体降低附加回报，阻止局部智能体以降低全局回报为代价提升本路口运行效率的情况发生，确保干线协调的整体最优性。

3 仿真测试

为验证本文模型的可行性与优越性，首先，将控制算法封装成软件模块，并基于Simulation of Urban Mobility 软件搭建仿真平台，并通过应用程序接口(Application Programming Interface,API)实现优化软件与仿真平台的信息交互。其次，设置仿真实验参数，确定最佳智能体设计方案，并对比新方法与传统方法的运行效果，验证新方法优越性。

3.1 实验设置

仿真路网包含3 个信号路口，几何布局如下：(1)3 个路口的进口道和出口道长度均为450 m，四周共有a～h 这8 个进出口；(2)所有进口道均包含3条车道，其车道属性由内向外依次是左转专用道、直行车道及直右共享车道；(3)路口均采用对称式放行的固定相位相序结构，包含南北直行、南北左转、东西直行及东西左转4 个相位，相位黄灯时间为3 s。仿真路网实验设置如图4所示。模型训练中，强化学习网络的参数设置如表1所示。

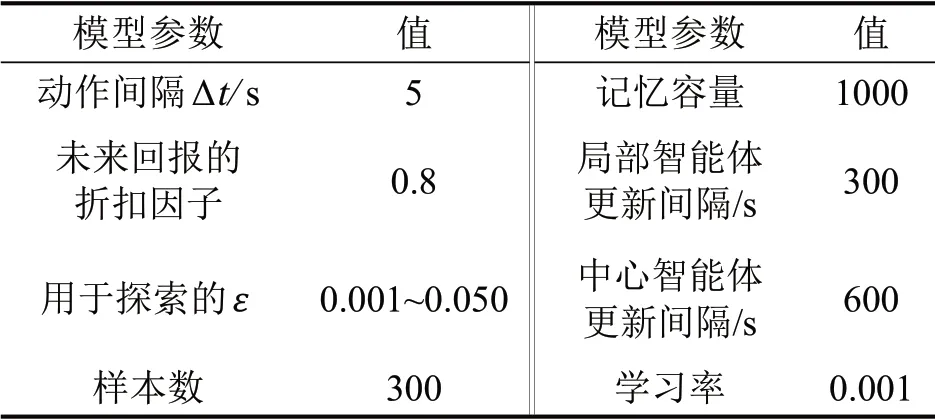
表1 参数设置Table 1 Settings for theproposed method

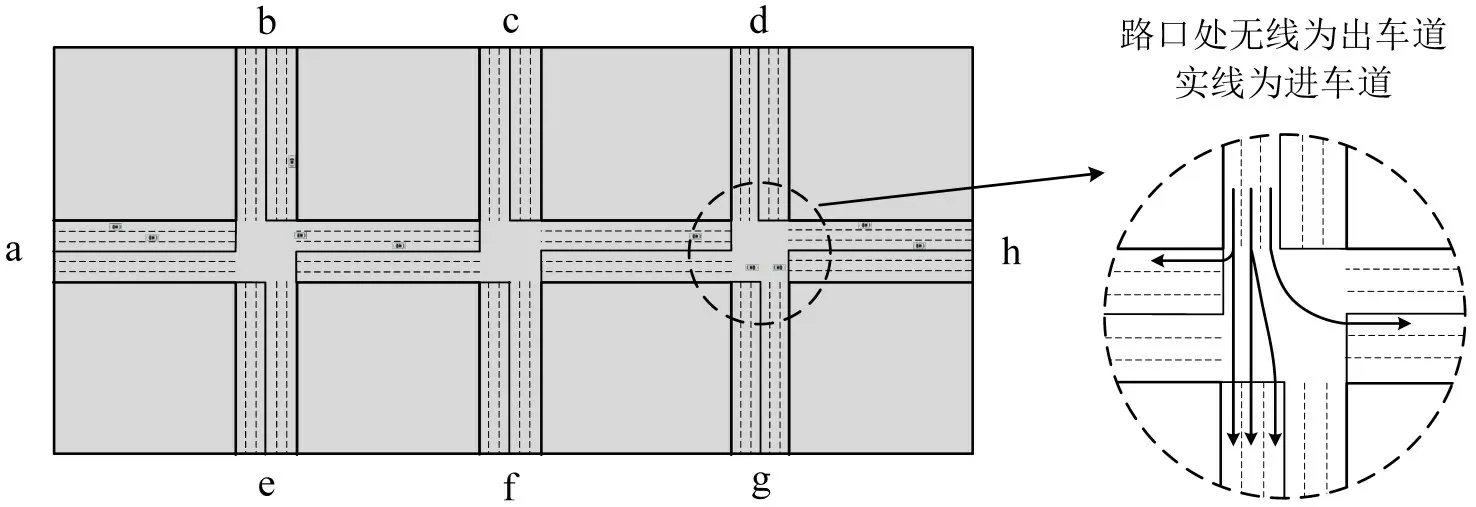
图4 实验设置Fig.4 Experiment settings

为确定优化模型的最佳参数，需对网络进行预学习。为使智能体充分挖掘多样化的交通状态特征，车辆的到达由具有一定到达率的泊松分布产生，预学习流量配置包含低、中及高这3 个阶段，如表2所示。此外，干线直行包括a→h和h→a这两个方向，流量设置相等；支路直行、干线左转支路左转车流设置方法类似。

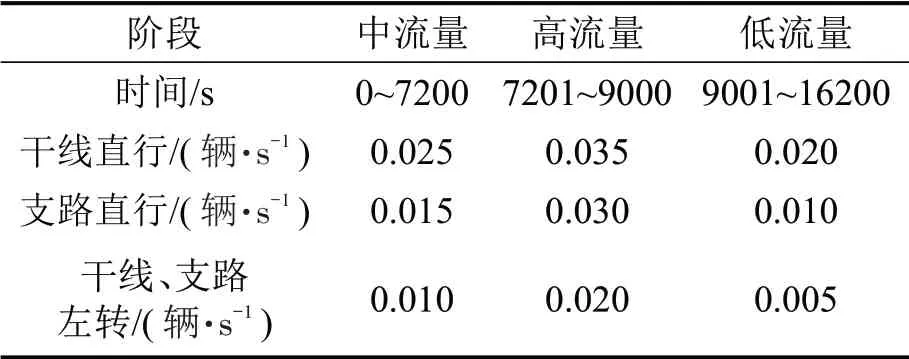
表2 训练流量结构Table 2 Configurations for train traffic flow

在测试阶段，参照实际路口的交通负荷设置4:00-22:00 这18 h 的交通流OD 矩阵，其中，早高峰(7:00-7:30)和午间高峰(12:00-12:30)的OD 分布如图5所示。

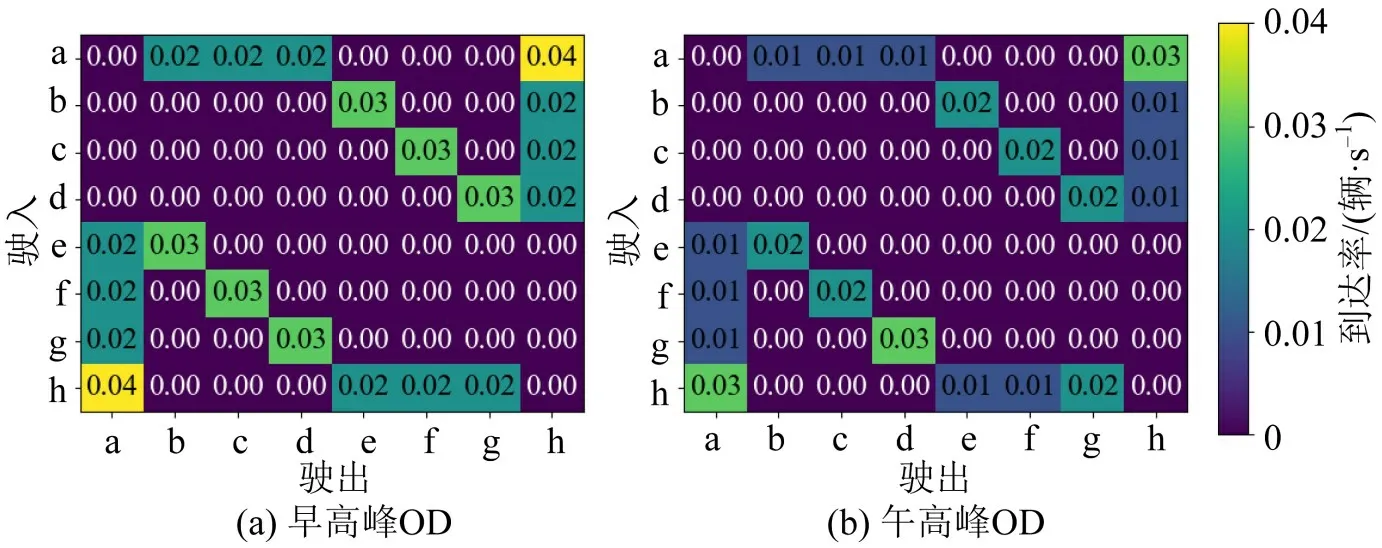
图5 高峰ODFig.5 Flow percentage of each OD pair

3.2 最佳局部智能体设计

首先，基于状态特征要素设置多组状态-回报方案，实验筛选3组最佳组合，进而，以干线排队长度、支路排队长度、干线停车次数、干线等待时间及支路等待时间5 个指标为依据对比分析不同组合下的控制效果。

组合1 状态空间包含进口道排队长度和承载车辆数等6个维度{L,Nin,W,S,Pc,Pn}，相应的回报函数为

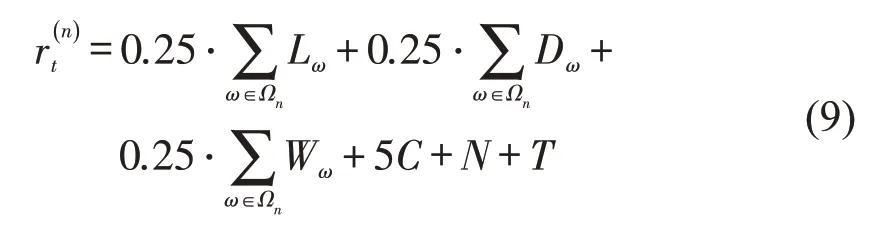
式中：Ωn为智能体n的进口道集合。

组合2 状态空间仅包含Nin和Pc两个维度，回报为进口道排队长度之和，即

与组合1 相反，组合2 的状态和回报均相对简单。

组合3 依据文献[7]的研究结果，信号优化应兼顾上、下游路段的负荷均衡，尽可能避免高峰时段的排队溢流现象。基于此，本文将所有出口道上车辆数Nout作为状态空间的元素之一，设计组合3 为{Nin,Nout,Pc}，回报函数同组合2。

在18 h 的测试时段内，3 种组合下的区域运行效率如表3所示。

组合3 在干线排队长度、干线停车次数、干线等待时间及支路等待时间等方面均显著优于组合1和组合2；干线协调下的控制目标是优先保障干线畅通，因此，组合3 的支路排队长度略高于组合2，符合既定目标。同时，在模型训练效率方面，组合2和组合3 的训练时间相当，均显著低于组合1。因此，从训练效率和模型效果两方面综合评估，组合3是最佳状态空间。测试时段内各评估指标的变化情况如图6所示。

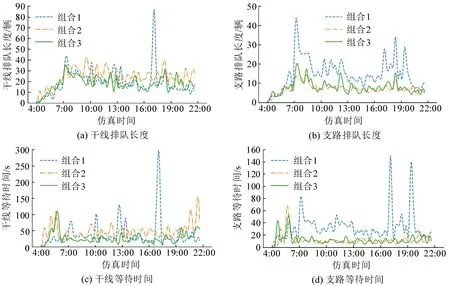
图6 3种局部智能体的测试结果Fig.6 Simulation results with three design methods for local agents

由图6可知，组合1 的支路排队长度和等待时间相对于其他两种组合均大幅增加，且在高峰时段出现极端拥堵情况，说明过于复杂的状态空间和回报函数设计不一定有利于信号控制。组合2 和组合3 的干线与支路等待时间相对稳定，组合3 虽然在支路上与组合2存在细微差别，但在干线排队长度和等待时间方面却有显著优势，在达到干线协调控制目标的同时提升了区域通行效率。

3.3 协同控制算法测试

为评估混合式协同方法的优越性，本文选取经典强化学习模型进行对比实验。为保证对比结果的公平性和可信度，对比方法和新方法均在最佳智能体模型的基础上进行参数调优。经多次调试，中心和局部智能体的回报函数分别为

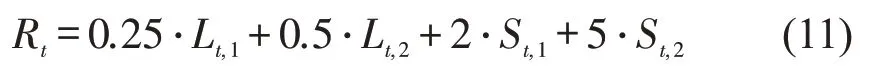
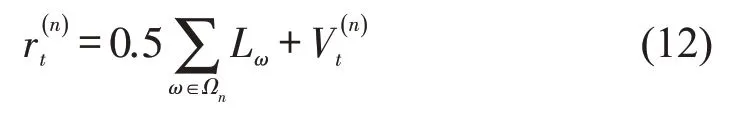
式中：Lt,1和St,1分别为相交道路进口道的排队长度和停车次数；Lt,2和St,2分别为干道进口道的排队长度和停车次数。

分布式协同是多智能体协同优化的常用策略，典型算法是深度MA2C网络[6]。该方法将衰减后的相邻路口状态和回报作为本路口的状态空间要素，局部智能体依据路口状态独立完成方案优化。为与本文方法保持一致，将局部智能体的算法改为本文相同的DQN算法。同时，为突出协调控制优势，将独立控制也作为一种参考方法，即单路口均采用独立DQN架构优化信号方案。

排队长度与等待时间在测试时段内的变化趋势如图7所示，汇总情况如表4所示。

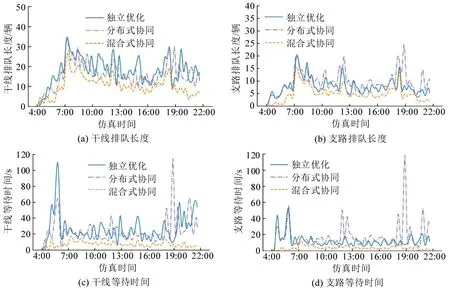
图7 协同控制测试结果Fig.7 Simulation results of different coordinated control methods

表4 协同方法结果对比Table 4 Performances of different coordinated methods

由图6和表4可知，分布式协同相对于独立优化降低了干线排队长度、等待时间及停车次数，但支路排队长度和等待时间却明显增加。因此，分布式协同没有较好地实现干线和支路的有效平衡。混合式协同的干线停车次数相对于独立优化和分布式协同分别降低了14.8%和13.6%。在干线等待时间方面，新方法相对于独立优化和分布式协同分别降低了73.3%和70.6%；同时，混合式协同的支路停车次数和排队长度接近或略优于独立优化和分布式协同，因此，新方法显著提升了区域交通流，尤其是干线交通流的运行效率。

4 结论

本文融合分区记忆、相位门控等技术，探究基于DQN算法的干线信号协同控制最佳智能体设计方法，搭建了智能体间的混合式协同决策优化流程。仿真实验证明，本文的智能体设计优于传统设计方法，且混合式协同可在保障支路交通流运行效率的基础上显著提升干线交通流通行效率。

为促使新方法可适用于实际工程，需进一步探索如下工作：(1)引入多样化的交通流量结构和相位相序结构，依据多类复杂场景不断充实模型架构；(2)设置不同规模大小的测试网络进行实验，验证方法的可拓展性；(3)突破仿真框架模拟测试的局限，基于真实数据学习现实世界的复杂反馈。