拥堵指数自适应调节的交通运行状态识别方法及应用研究

陈鼎，周水庭，陈云，苏敏咸

(1.厦门理工学院，机械与汽车工程学院，福建厦门 361024；2.厦门大学，航空航天学院，福建厦门 361102；3.厦门市卫星定位应用股份有限公司，福建厦门 361006)

0 引言

随着我国城市化进程的稳步推进，城市交通基础设施扩张的同时，也带动了城市人口快速聚集以及机动车保有量的增长，然而，两者的非对称性增速问题，极容易造成城市交通拥堵状态频发，严重情况下甚至影响了城市化质量[1]。因此，建立有效识别城市交通运行状态的方法，对于促进城市交通路网与城市规划协调发展具有理论与现实意义。

针对交通运行状态识别问题，现有研究主要从指标分级与建模分析两个方向展开。指标分级方法是以交通单一物理量作为指标变量[2]，如平均速度、出行时间、流量等，依据道路速度、时间占有率、流量分散程度等为阈值进行交通运行状态的等级划分。指标分级方法为城市交通运行状态的评估提供了经验数据和阈值区间标准，但由于此类方法的数据来源以道路监测设备数据为主，故主要用于解决宏观或静态的交通运行状态评估问题[3]。建模分析方法是结合浮动车历史数据与路网模型，对微观或动态层面上交通流状态进行观测的方法。WANG 等[4]提出了一种基于浮动车和道路感应线圈数据融合的交通状态识别模型，采用数据可视化技术实现了车辆速度与交通拥堵状态的交互式分析过程。HSUEH 等[5]基于道路网络的距离信息和拓扑结构等空间特征，提出了车辆与路网匹配的STD-Matching 算法，用于计算道路速度约束及车辆行驶路径，该项研究内容为交通拥堵识别提供了建模和数据可视化条件。SHIRMOHAMMADI等[6]建立了以车辆平均速度和道路限速为变量的拥堵指数模型，分析了路网的交通流密度，并结合神经网络和遗传算法实现了对车辆速度和交通拥堵状态关系的预测。相较于指标分级方法，建模分析引入了车辆动态参数，这使得模型具有分析交通拥堵时空特征的能力。

国内学者在交通运行状态识别方面也进行了相应的研究。王璐媛等[7]对已有交通运行指数进行了归纳和总结，并提出动态运行指数模型在测算交通运行指数中的重要性。王妍颖等[8]基于通讯大数据展开交通拥堵状况的评价分析，充分考虑了平均旅行时间指数TTI、概率出行时间指数PTI、延误、交通拥堵时间等指标，并对比分析了不同指标体系下北京市交通拥堵的变化规律。王晓旭等[9]提出了时空并置模糊拥堵模式概念，并结合路网属性和道路拓扑结构信息对交通运行状态进行模式挖掘分析。朱敏清等[10]基于全方位视角场景的驾驶人主观拥堵感知实验，建立了主观拥堵状态下路径调整行为模型，探究交通拥堵的形成机制和扩散规律。

综合上述研究内容，交通运行状态分析主要以道路速度作为参变量，而其中的畅行速度仍是通过经验阈值和速度统计分布规律获得，无法依据历史数据的时空特征进行自行调节，降低了相应拥堵指数的计算精度，影响交通运行状态识别的实时性。因此，构建依据道路速度自适应调节的拥堵指数模型，即成为本次研究中需要解决的关键性内容。本文采用ST-Matching算法对浮动车轨迹与路网数据进行匹配融合，通过概率密度分段函数挖掘浮动车所处道路的速度-时间分布区间，以此构建具有自适应调节的拥堵指数模型，在此基础上，结合拥堵指数分级指标对厦门市交通运行状态进行识别应用。该方法有别于采用固定平均速度的交通拥堵指数计算方法，分析所得城市交通拥堵时空分布同时也反映了城市路网的结构特点，这对于快速建立不同城市的交通运行状态识别系统起到积极作用。

1 浮动车数据处理与地图匹配

1.1 浮动车数据预处理

浮动车是指装备了全球卫星定位系统(GPS)的公交车、出租车与网约车等营运车辆。由于浮动车的出行特征和驾驶习惯相较非营运车辆更为统一，因此浮动车数据常作为交通信息数据库的组成部分。浮动车数据以车辆行驶状态数据为主，数据字段包含车辆代码、GPS 定位信息、运营状态和订单号信息等。GPS定位信息中，GPS时间、经纬度、速度和方向是浮动车与路网数据进行时空匹配的重要字段。

将m行浮动车数据A划分为n段，构成数据集合A[i](i=1,2,…,n)并进行数据预处理，以此提高计算效率。浮动车数据具有低、中、高这3 种不同采样频率，一般认为采样时间间隔高于30 s的为低频采样，低于10 s 的为高频采样，介于两者之间的为中频采样。为了保证可用数据的占比率，首先，以采样频率30 s 作为采样阈值δ对GPS 时间数据进行划分；其次，以城市行政区划剔除市域边界外的浮动车GPS经纬度数据及其对应元组，在此基础上对局部脏数据进行清洗，包括剔除数据空值、重复值、离群值；最后，关联浮动车订单号与运营状态，保留同时满足订单号非零及运营状态标识为“1”的数据元组。通过上述预处理后的浮动车数据集合A[i]可用于路网数据的匹配以及后续的数据分析过程。浮动车数据预处理流程如图1所示。

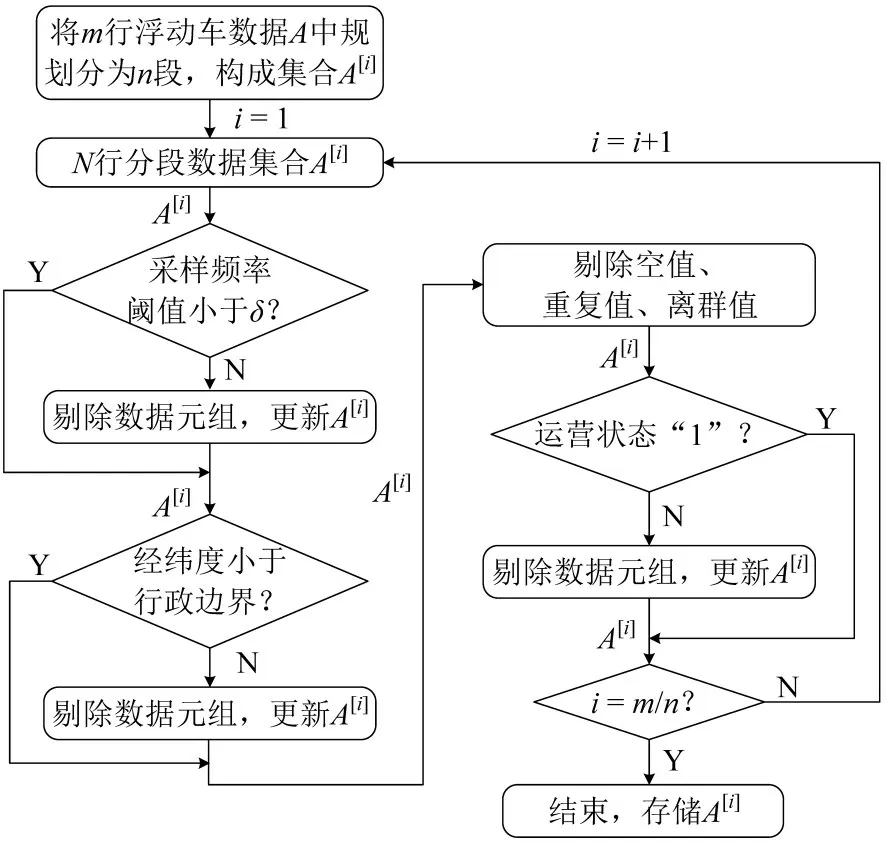
图1 浮动车数据预处理流程图Fig.1 Preprocessing flow chart of floating vehicle data

1.2 浮动车与路网数据匹配

浮动车与路网数据匹配是交通运行状态识别的关键环节。由于受到设备、卫星信号等诸多因素影响，浮动车与路网数据通常存在一定的偏差，因此需要将浮动车行驶轨迹数据与路网地图信息进行匹配。在数据层面上，该过程的核心思想本质上是解决平面线段序列的模式匹配问题。现有地图匹配算法主要从局部/增量、全局和概率层面进行构建，近年来，随着城市交通的快速发展，交通运行状态数据的采集与维护成本越来越高，低频采样需求开始增大，这使得采用全局层面和利用低频采样数据的地图匹配算法得到广泛应用，如隐马尔科夫模型HMM、IF-matching和ST-matching算法[5]。

本文采用计算成本与中低频采样适配的STMatching 作为浮动车与路网数据匹配算法。STMatching 算法中假定浮动车 GPS 轨迹T=(P1,P2,…,Pi,…,Pn)，以半径r检索行驶路段ei上的Pi点，计算Pi与ei距离最小的点作为候选点投影集合c，距离检索规则表示为

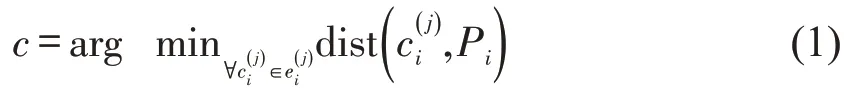
式中：下角标i用于标记轨迹T中的被检索点Pi；为行驶路段ei上的待检索点，上角标j用于标记待检索点；为与Pi点间欧氏距离。

基于浮动车GPS 坐标点Pi与投影集合c中元素之间的距离，以及GPS测量误差的正态分布规律N(μ,σ2)，μ与σ分别表示距离的均值和标准差，在不考虑邻居点Pi-1检索结果的情况下，单一GPS 坐标点Pi在行驶路段ei上与投影点相匹配的观察概率为

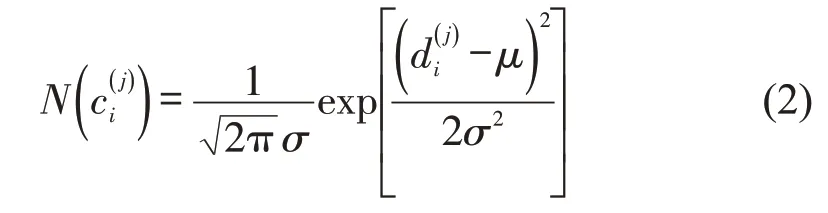
进一步将邻近坐标点Pi-1、投影点与引入，其中，t,s分别为两相邻待检索点标记j中的取值。由于Pi-1到Pi在实际路段上的概率与投影点到的最短距离相关，因此构建Pi-1、Pi间欧氏距离dist(Pi-1,Pi)与、在行驶路段ei上的最短距离w(i-1,t)→(i,s)之间的比值，用于表征相邻两投影点与间距离的差异程度，即

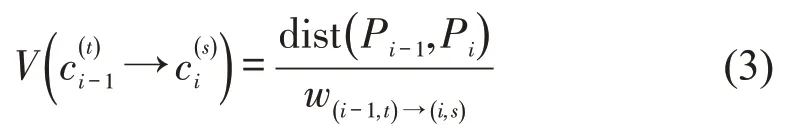
结合式(2)与式(3)，浮动车GPS 轨迹T中元素在行驶路段上投影集合c的空间分析函数表示为

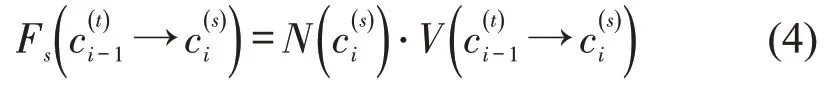
式中：与分别为GPS 坐标点Pi-1和Pi在行驶路段ei上的检索投影点。

依据投影点与对行驶路段ei进行k段分割，分割路段ek长度lu的总和则可用于近似表征行驶路段ei的平均速度，即

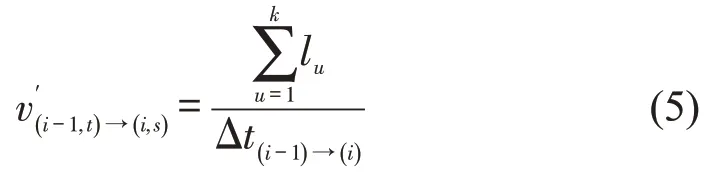
当存在两组投影点使得GPS 坐标点Pi-1和Pi在空间分析函数结果存在近似结果时，考虑邻近相同长度lu的路段，引入余弦距离测量投影点平均速度与该行驶路段设计速度vu之间的相似性[5]，时间分析函数则表示为

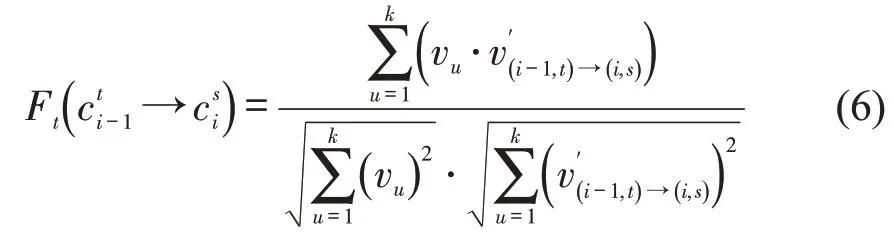
结合空间分析函数式(4)与时间分析函数式(6)，浮动车与地图时空匹配计算公式为

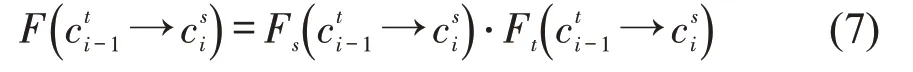
2 基于概率密度分段的自适应拥堵指数模型

拥堵指数模型是交通运行状态识别的主要方法之一，通常是建立在针对时间或速度的观测和期望数值基础之上，并可以通过行驶路段长度进行转化计算[7]，即

式中：η为道路拥堵指数；v′为该道路行驶车辆的平均速度；vd为期望车速；th为该道路平均出行时间；tf为自由流状态下出行时间。

式(8)中，期望车速vd是以道路自由流状态下速度累计分布曲线上的第85分位所对应数值作为计算依据，结合道路等级、设计时速以及专家打分进行换算。然而，由于速度累计分布曲线无法反映统计值所处时段，这使得期望车速vd可能同时包含了道路繁忙时段(忙时)和空闲时段(闲时)的车速统计值，进而导致计算结果低于实际车辆畅行通过道路时所需速度[5]。为解决这一问题，通过空间匹配后的期望车速vd需要进一步引入时间特征，以此满足区分期望车速vd所处时间段的目的。对GPS时间t进行排序并划分为N段，每段时间中所具有的车辆平均速度v′标记为两个相等数量的样本数据g和h。对道路限速进行区间划分，当道路限速100 km·h-1时，以5 km·h-1递增则等分区间数M=20 份，通过计算样本数据g和h在概率密度曲线中任一小区间L(L≤M)中的积分值，获得g和h落入M中所具有概率pL,g和pL,h，同时构建了GPS时间t与对应速度区间的概率pL,g和pL,h之间的关系，如图2所示。

将GPS时间t与概率pL,g和pL,h作为两组关联数据，采用式(3)中欧氏距离方程建立用于表征两组关联数据之间差异程度的间距方程，这一过程与式(3)在处理空间距离差异性方面具有相似的物理意义。通过速度概率pL,g和pL,h的差异性获得GPS时间t的分段结果，以此达到选择畅行速度计算时段的目的。结合图2概率密度分段原理图，划分为N段GPS 时间t所对应任意两段样本数据g和h之间的间距为

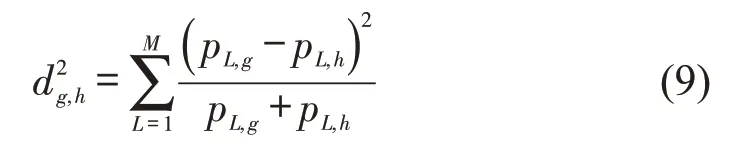
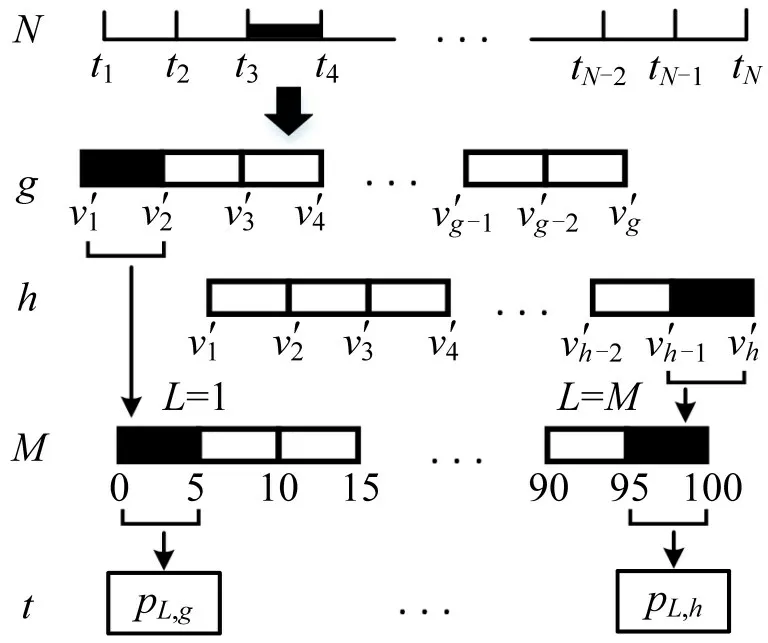
图2 概率密度分段原理图Fig.2 Schematic diagram of probability density segmentation

以主干道和次干道路段的匹配数据为例，设定GPS时间分段数为N=20，每段数据中GPS速度被标记为相等数量的g和h个小样本；道路限速100 km·h-1，以5 km·h-1递增并等分M为20 份；计算小样本数据g和h落入第L个小区间的概率pL,g和pL,h，并代入式(9)计算N段数据中任意两段之间的数据间距d2g,h，绘制样本数据间距-时间分布图，如图3所示。

由图3可知，样本数据间距-时间分布图被划分为明显的3 个区间，这说明3 个区间之间的样本数据距离d2g,h存在显著差异性。由于样本数据来源于每段GPS 时间t，样本数据间距-时间分布图的区间结果同时也反映出时间上的对应分段现象。各区间之间的车辆平均速度概率间距d2g,h均大于0.2，以此为阈值将全天时段内道路状态划分为运行区间和畅行区间，区间所对应时间分段与实际道路中的忙、闲时段相吻合。由于00:00-7:00 时段的数据量相对较少，且容易与忙时时段落在同一分段区间内，考虑主干道中晚间时段21:15-24:00，次干道20:00-24:00作为畅行区间更为合适，由此弥补了速度累计分布曲线无法反映时间特征的缺陷，如图3中畅行区间标记所示。

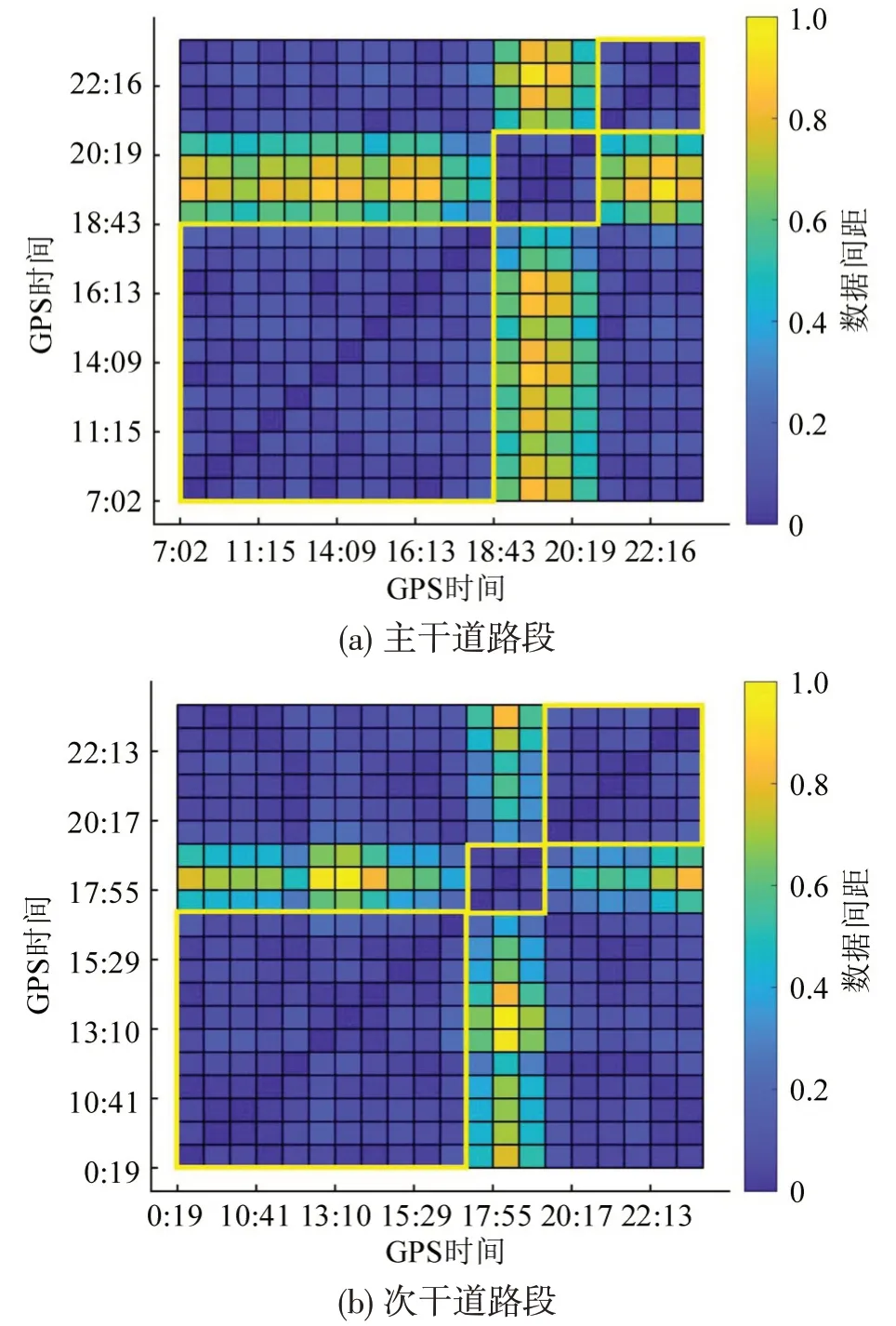
图3 样本数据间距-时间分布图Fig.3 Sample data interval-time distribution

将样本数据间距-时间分布中速度偏差最大值作为分段阈值，其中正向偏差位于畅行区间起始点(g,h)，那么对应区间(g,h)→(M,M)内的平均速度则可定义为畅行速度v0，计算公式为

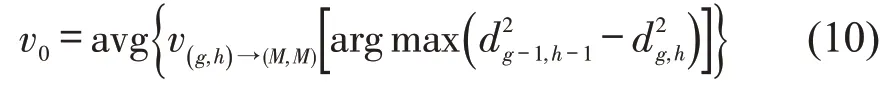
将式(10)与式(5)相结合，在投影点与之间，相同分割路段ek长度lu的总和条件下，拥堵指数则可通过平均速度v′与畅行速度v0计算，式(8)中道路拥堵指数η由此可以转化为

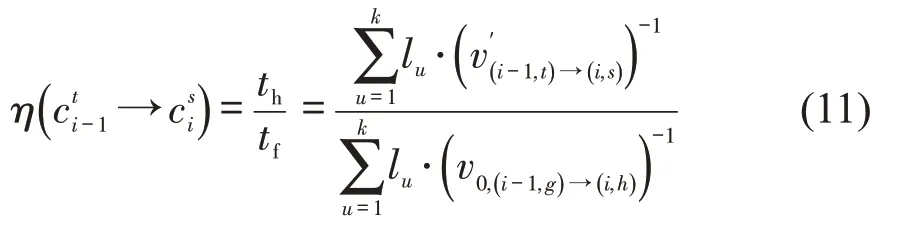
式(11)将匹配数据中的浮动车平均速度v′与该道路畅行速度v0进行融合，拥堵指数η随着浮动车速度的变化，并通过样本数据间距-时间分布进行自适应调整，这为城市周期性交通拥堵预测问题提供了数值基础。此外，基于指标分级方法中对于拥堵指数和速度的划分区间[9]，将交通运行状态调整为畅通、缓行、拥堵和极度拥堵状态，依据式(8)计算相同路段长度条件下的观测和期望时间比值，以此作为拥堵指数阈值与交通运行状态之间的划分关系，如表1所示。

结合浮动车匹配道路等级，式(11)计算结果落入表1中拥堵指数区间则反映交通运行所处的状态。此外，由于式(10)与式(3)在判断数据间距离上具有相似性，两者均基于概率密度求解数据集在相应速度或空间区段内的距离，因此可以将式(10)整合至地图匹配算法中进行统一求解。

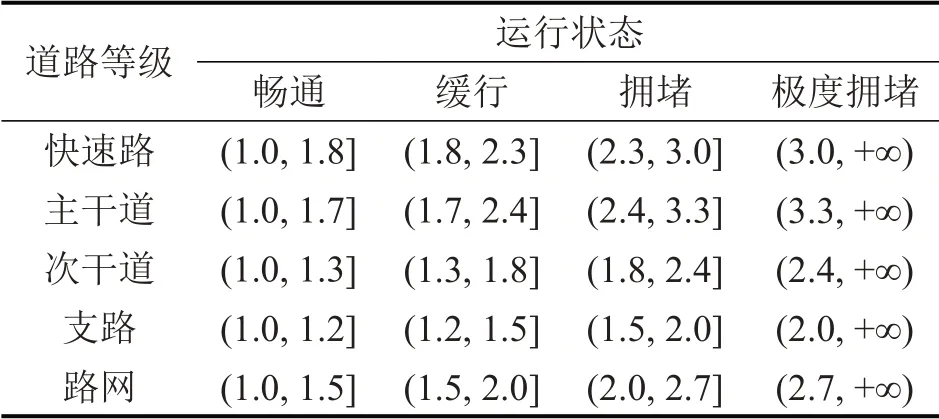
表1 拥堵指数阈值及交通运行状态划分Table 1 Congestion index threshold and traffic performance division

3 仿真结果分析

采用厦门市2019年6月6日节假日浮动车数据作为数据来源，MATLAB 数值分析软件作为仿真工具进行仿真应用分析，其中包括数据预处理、ST-Matching 算法的匹配效果、拥堵指数模型的自适应特性，以及两者相融合的城市交通运行状态识别应用分析。

3.1 浮动车数据预处理与路网匹配结果分析

依据图1对浮动车数据进行预处理，数据处理前后的字段、数据类型、数据行数对比结果如表2所示，其中，满足模型计算要求的有效数据占比达到原数据的76%。将浮动车预处理数据代入式(1)～式(7)与厦门市路网数据相匹配，匹配结果以复杂互通立交(杏林互通立交桥-杏滨路路段)和专用共线道路(滨海西大道)为例进行展示，如图4所示

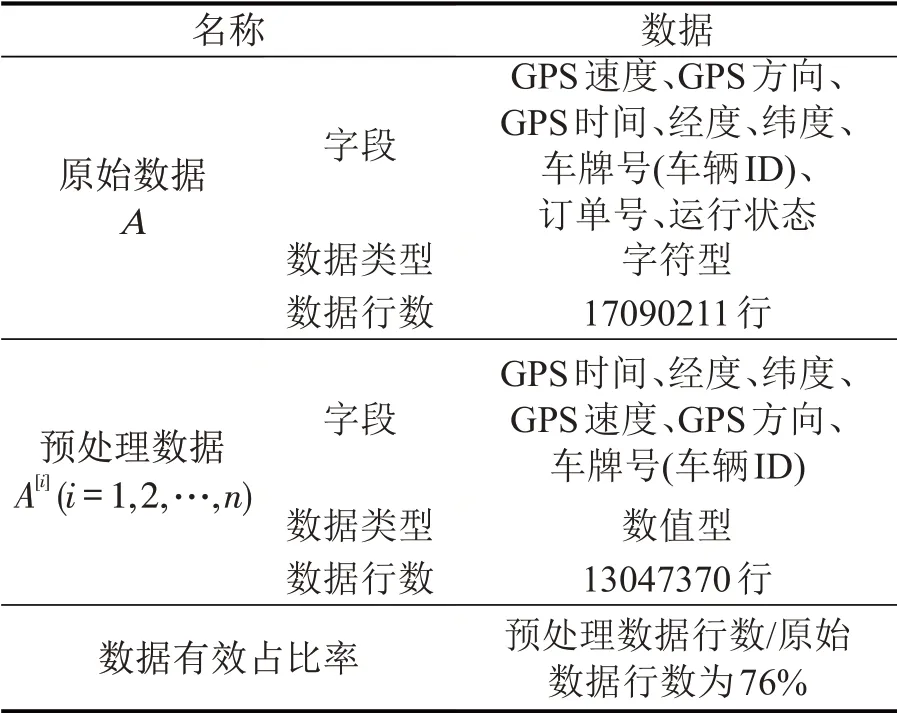
表2 浮动车数据处理结果Table 2 Floating vehicle data processing results

图4中，ST-Matching算法将原有偏离路段的浮动车轨迹点(空心圆标记)匹配至相邻最近且与前后轨迹点(实心圆标记)保持一致的路段中。杏林互通立交桥-杏滨路路段为双向主干道与辅道(主干道连接线)相结合形式，匹配后的浮动车轨迹点在进入与离开互通立交方向均与立交跨线方向一致，如图4(a)所示；滨海西大道为BRT专用道路与主干道共线路段，浮动车投影点远离旁支辅道并始终保持主干道运行，如图4(b)所示。

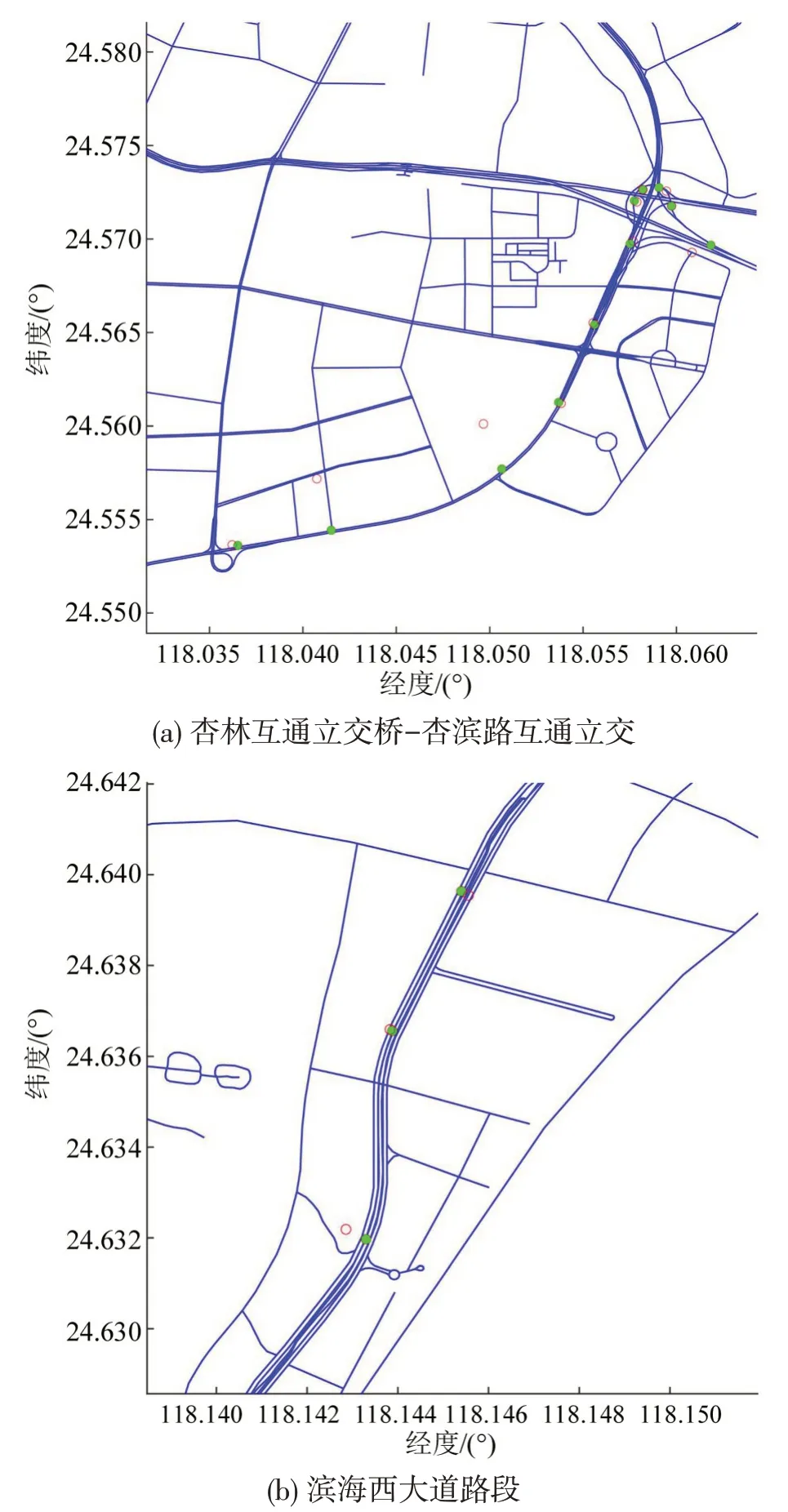
图4 浮动车与路网数据匹配结果Fig.4 Data matching results between floating vehicle and road network

3.2 自适应拥堵指数模型仿真分析

以图4中两路段浮动车轨迹T及其匹配道路路段ei进行仿真分析，计算GPS时间历程相关的道路平均速度v′、畅行速度v0及拥堵指数η，并与已有方法进行对比分析，以此论证模型可行性。自适应拥堵指数模型仿真结果如图5所示。

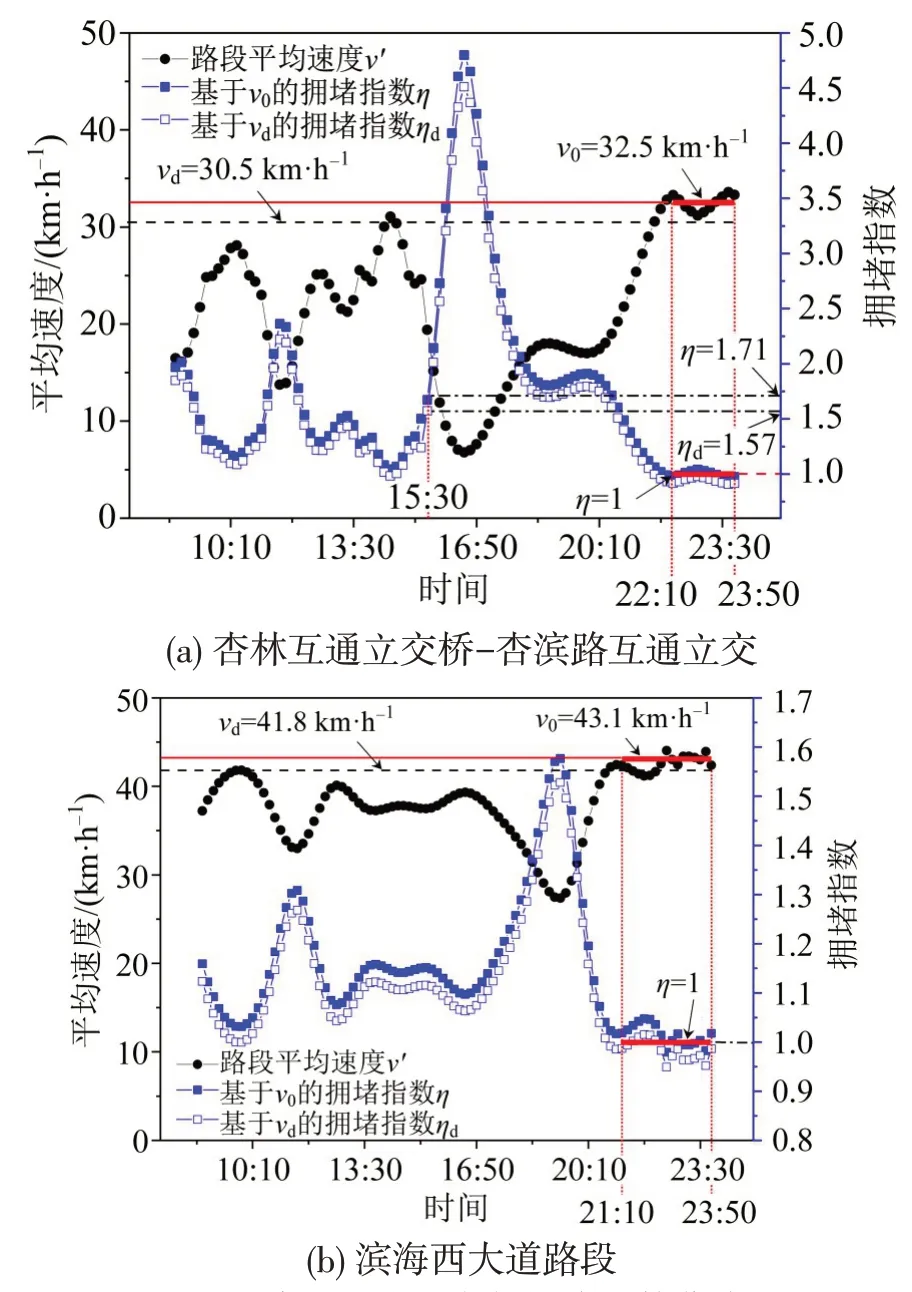
图5 路段平均速度与拥堵指数曲线Fig.5 Curve of average road speed and congestion index

图5(a)中，集美区与杏林区双向互通的杏林互通立交桥-杏滨路路段全天平均速度v′相较于滨海西大道路段普遍偏低，这与其双向互通导致车辆流线交叉的客观现象相吻合。高峰时段(15:30-20:00)该路段出现全天最低速运行状态，平均速度v′介于5～20 km·h-1之间，对应拥堵指数η分布在1.7～5.0之间，属于典型的下班晚高峰拥堵运行状态。相同时段内滨海西大道路段平均速度v′处于25～40 km·h-1之间，对应拥堵指数η分布在1.0～1.7之间，如图5(b)所示，由于该道路为普通南北走向主干道，同时具有次干道衔接分担一部分车流量，因此该道路全天运行状态为畅通状态。

图5中，v0为依据样本数据间距-时间分布图识别的畅行速度，分别为32.5 km·h-1和43.1 km·h-1，畅行区间时间分布在晚间闲时时段21:00-24:00，由于该时段内整体车流量相对白天更小，辅路和次干道的车流交叉较少，符合道路畅行的实际运行状态。vd为两路段全天速度累计分布曲线的第85 分位数数值，分别为30.5 km·h-1和41.8 km·h-1，相较于畅行速度v0降低了6.1%和3.0%，主要原因是采用全天速度累计分布进行计算，容易将道路运行时段高流量状态下的平均速度引入考虑，该道路夜间车流密度越少，第85分位数则越偏离畅行速度要求，如图5(a)中畅行速度标识所示，该路段全天经历畅行至极度拥堵运行状态，车流密度变化剧烈，采用速度累计分布曲线计算畅行速度误差相应增大。

依据v0和vd计算拥堵指数η和ηd，如图5所示，两路段中η相较ηd增大了6.5%和3.2%，但是由于畅行速度偏差的存在，这使得主干路阈值处的ηd计算结果仍偏于保守。例如，图5(a)中路段的晚高峰从15:30开始，此时基于vd计算的拥堵指数ηd为1.57，识别道路运行状态仍然为畅行，但自适应拥堵指数η=1.71 识别交通运行状态为缓行，这使得后续时段中采用vd识别的道路运行状态均落后于自适应拥堵指数模型计算结果。相同的现象也发生在图5(b)路段中。此外，由于vd数值偏离全天最大畅行速度v0，这使得ηd在夜间道路运行速度较高时出现低于数值1的现象，与道路处于畅行状态时浮动车平均速度v′即为畅行速度的假设相违背，同时也不利于后续数据可视化及其含义解释。

综合上述仿真分析结果可以发现，结合浮动车与路网匹配数据，采用复杂互通立交和专用共线道路验证了畅行速度v0及自适应拥堵指数η的适用性，其计算结果相较传统方法更为符合道路实际运行状态。

3.3 城市交通运行状态应用分析

以厦门市城市快速路、主干道、次干道中的浮动车和路网数据为应用对象，采用自适应拥堵模型计算城市交通平均拥堵指数曲线，并依据表1中路网拥堵指数阈值对交通运行状态进行划分，计算结果如图6(a)所示，从中可以发现，2019年6月6日全天交通运行的缓行状态为7:30-8:20、15:10-16:10、21:00-21:30；交通运行拥堵状态分别发生在16:10-17:00，以及19:20-21:00，两时段起止时间点分别与下班晚高峰的起止时间点相吻合。厦门市交通极度拥堵状态发生在17:00-19:20，平均拥堵指数均大于2.7，最高峰值位于18:20，其值可达到2.79。

提取18:20 时段的道路拥堵指数，并将其映射至路网数据中，获得拥堵空间分布如图6(b)所示。图6(b)中，厦门市进出岛方向交汇路段均发生不同程度的拥堵现象，这说明进出岛方向的道路设计等级标准、桥隧数量与行驶车辆数量之间存在非对称性，同时也反映了城市居民和游客在晚高峰时段出行意愿与城市交通拥堵时间特征之间的关联性。在拥堵空间特征方面，厦门岛内东西方向主干道和出岛快速路的拥堵状态最为严重，例如莲前西路、仙岳高架、环岛路(旅游景点：白城沙滩至曾厝垵方向)、环岛干道，交通拥堵长度相较南北方向更长，这与厦门市的商业中心、旅游景点呈现沿海岸线东西方向分布相关联，这一现象在节假日时表现得更为明显。

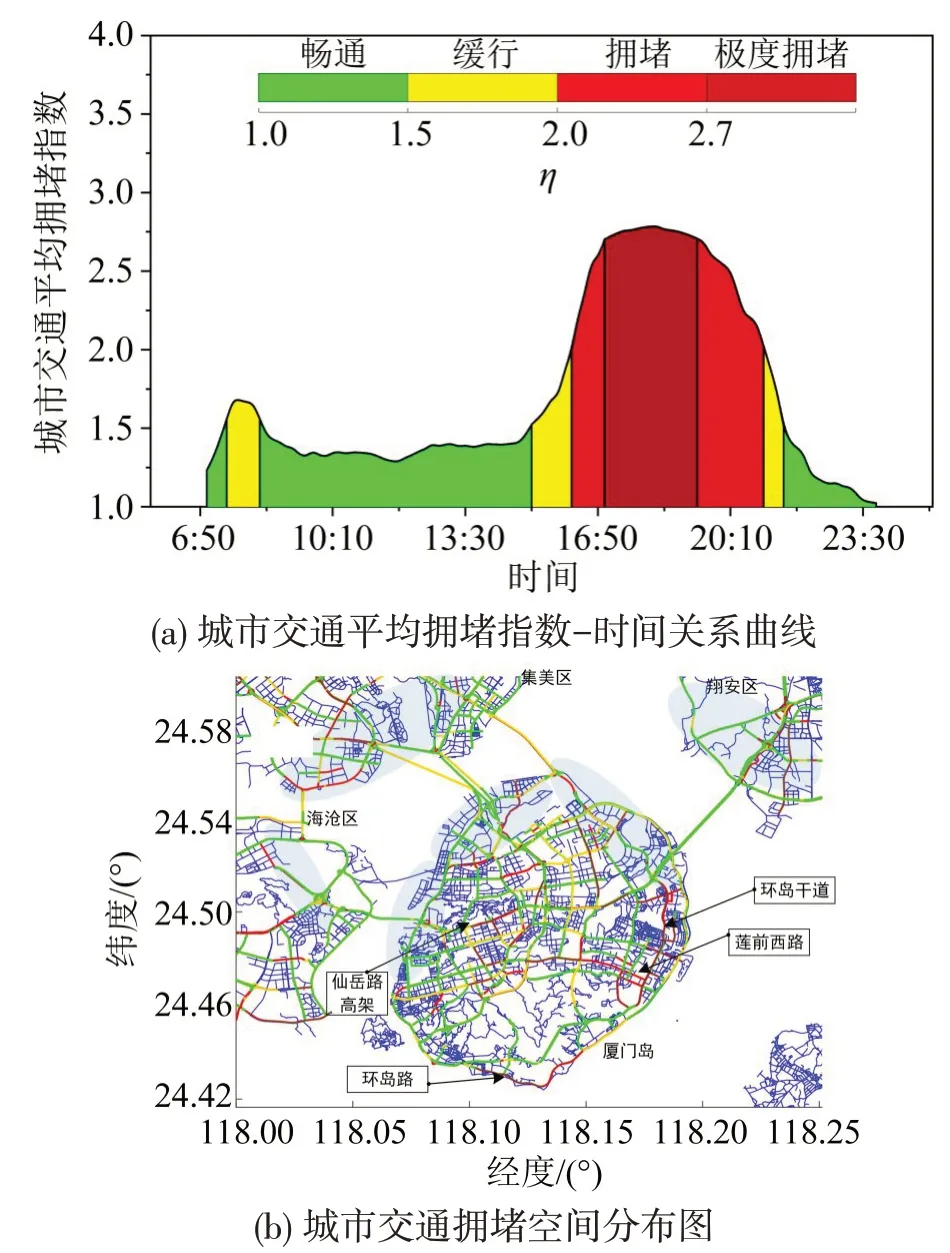
图6 城市交通运行状态识别结果Fig.6 Recognition results of urban traffic performance

综合上述分析结果，采用自适应拥堵指数模型对交通运行状态进行评价，可以进一步为交通规划提供方法与数据支撑。厦门岛与外围海沧区、集美区和翔安区可以采用拓宽车道、增加桥隧数量的方式，提高交通运行高峰时段的车辆分流效率，以此缓解岛内外进出主干道、次干道的交通压力。例如将已有厦门岛-集美区的双向4车道海提路扩建为双向6 车道，或将翔安区进行桥、隧相结合形式的线路改造，这对降低路网拥堵持续时间、改善城市交通运行状态具有积极改进作用。本文提出的基于拥堵指数自适应调节的交通运行状态识别方法，仅针对厦门市2019年6月6日节假日的浮动车数据展开试验论证，后续将结合季度或年度数据展开预测研究工作。在改善指标分级方法方面，结合出行时间与道路V/C 比等混合指标，将节假日、交通管制等特殊因素的影响引入交通运行状态识别过程中，进一步拓展方法的应用场景范围。

4 结论

本文通过对浮动车与路网数据匹配和挖掘分析，构建了具有自适应调节能力的拥堵指数模型，以此构建了城市交通运行状态的识别方法，所得结论如下。

(1)通过复杂互通立交和专用共线道路的浮动车匹配结果，验证了ST-maching算法对于中高频浮动车采样数据的适用性。

(2)基于概率密度分段原理建立的自适应拥堵指数模型能通过匹配数据中GPS 速度间距的最大偏差位置判定道路忙时和闲时的分段阈值点；计算所得样本数据间距-时间分布弥补了传统速度累计分布曲线在反映时空特征方面的不足，在识别的畅行区间中，分别保留了速度和时间参变量；样本数据间距-时间分布识别的畅行区间速度v0，相较于速度累计分布曲线的第85分位数vd偏高。

(3)结合指标分级方法，自适应拥堵指数模型计算的厦门市节假日交通运行状态及其路网阈值范围为：畅通状态(1.0,1.5]，缓行状态(1.5,2.0]，拥堵状态(2.0,2.7]，阈值大于2.7 为极度拥堵状态；厦门市城市交通运行状态呈现单一晚高峰拥堵形态，平均拥堵指数分布在1.0～3.0之间。厦门市节假日交通拥堵时段、极度拥堵时段集中在16:10-21:00，峰值数值为2.79，拥堵路段主要集中在东西方向主干道和出岛快速路中。