蜂窝梁在大跨度结构中的设计与应用

王燕玲

（山西工程职业学院，山西 曲沃 030000）

0 引言

近年来随着我国经济的快速发展， 新型建筑体系——钢结构建筑得到大力发展， 但是总体形势还是落后于发达国家。 对于我国钢结构建筑发展的一个主要限制因素就是造价问题。 要促进钢结构建筑在我国的发展， 就需要科技工作者努力探索和寻求节约钢材的理论和方式， 达到降低钢结构建筑造价的目的。

从利用梁的受力特性考虑设计梁的截面结构，近年来应用较多。 研究表明，在相同的承载条件下，与实腹梁相比，设计和使用蜂窝梁可减少钢材使用量达到总耗量的25%～30%，同时节省油漆和运输安装费用15%～34.6%， 具有良好的经济效益。 结合我国国情，更适于在大跨度结构设计中推广应用[1]。

1 蜂窝梁的特点

（1）作为一种新兴的钢结构，蜂窝梁在传统钢梁的基础上，采用特定的截面形式进行裁切，重新连接构成一种新型的钢梁。

（2） 不同的开孔截面形式和开孔数目，可以将蜂窝梁分为圆孔型蜂窝梁、椭圆孔型蜂窝梁，六角孔型蜂窝梁及八角孔型蜂窝梁等。蜂窝梁孔截面形式的不同会影响到梁的整体受力性能。现阶段应用较多的是六角孔蜂窝梁。

2 蜂窝梁的受力性能分析方法与计算

2.1 正截面强度验算

蜂窝梁的实腹部分强度验算按照实腹梁来验算。 蜂窝梁空腹部分T 形截面按以下计算：

2.1.1 截面正应力计算

蜂窝梁的空心部分根据T 形截面的正应力进行校核。在纯弯曲梁的情况下，空心T 形截面的弯曲应力是在弯矩Mx 的作用下产生的。如图1（a）所示，其呈现矩形分布。当蜂窝梁受剪力作用时，空心截面中的总剪力根据上下T 形截面的刚度分布。 每个孔的垂直中心线出现剪力弯矩，如图1（b）所示[2]。

图1 蜂窝梁应力分布

可得计算如式（1）所示。

式中V 代表截面总剪力。

根据此计算式中的假定， 在图b 中，b 点和c点处，即在上下对称的截面中，位于腹板角点处的两点，是最大正应力的作用点。

对于如图所示的上下对称型截面，蜂窝梁的抗弯强度计算如式（2）所示。

式中：Mx、V―蜂窝梁验算截面处产生的弯矩和剪力；AT―梁T 形截面的净面积；hz―桥部上下T 形截面的重心距；a―桥的跨度；WT―梁T 形截面的腹板边缘处的净截面模量。

根据以上讨论，危险截面一般与弯矩最大的断面或剪力最大的断面不重合。

当有且仅有载荷均匀地分布在简支梁上时，在距离梁端x 附近的蜂窝孔中点处时梁的危险截面，此处截面应采用抗弯强度Mx 和V 来校核抗弯强度。

距离x 的计算如式（3）所示：

其中l 为蜂窝梁的跨度。

除以上荷载情况外，其他载荷形式下的梁，不需要计算危险截面，通常在梁端第一个开孔处的中央、0.25 跨度处和0.5 跨度处分别进行相应验算[3]。

2.1.2 切应力验算

（1）T 形截面处的切应力计算如式（4）所示。

式中：ST―T 形截面的静矩； 当形心位于内翼缘内表面之间时，取腹板面积对形轴的静矩，当形心位于腹板内时，取中性轴以上部分面积对中性轴的静矩；IT―T 形截面的惯性矩。

（2）当切应力的作用处位于两个相邻的支座中两个临近的孔洞之间的墩腰处的焊缝上时，其计算如式（5）所示。

若是墩心焊缝采用剖口焊缝可不比验算。

2.2 刚度验算

由于蜂窝梁中腹板开孔的性质，腹板的剪切变形较大，因此在计算蜂窝梁的挠度时，剪切变形的影响非常重要。 剪力会造成两个方面的挠度，一方面挠度来自剪力引发的次弯矩，另一方面挠度来自剪力产生的剪切形变。

蜂窝梁的总挠度计算如式（6）所示。

这是蜂窝梁挠度计算的理论方法，在实际计算时需要求出较多参数。包含蜂窝梁上下截面的惯性矩、孔洞间腹板部分的抗弯刚度。 所以通常在计算蜂窝梁的总挠度时，一般采用下列公式进行估算

式中：f—挠度扩大系数， 此系数的影响因素包括：开孔截面尺寸、h/L、h/H、 荷载类型、 孔的形状等；fSM—实腹梁的计算挠度，该实腹梁的截面与蜂窝梁未开孔部分相同。

2.3 稳定性验算

蜂窝梁的侧扭屈曲临界弯矩可通过在平面内增加由弯矩作用产生的变形而得到提高。故对蜂窝梁讲，当梁在弹性范围内工作时，不考虑弯矩作用平面内的变形， 可借助实腹钢梁整体稳定性公式，计算得到的蜂窝梁临界弯矩是偏于安全的。故现阶段对于蜂窝梁的整体稳定性计算是参照实腹梁的稳定性计算原则，并作修正，计算如式（8）所示。

式中：k 为修正系数。

蜂窝梁翼缘局部失稳时， 可采用下列公式验算。 因为该情况下蜂窝梁与实腹梁基本一致，所以将蜂窝梁该部分拆分成三块进行验算。

（1）上下翼缘外伸长度与翼缘厚度之比：

（2）实腹部分截面高度与腹板厚度之比：

（3）桥部T 形截面的腹板高度与腹板厚度之比：

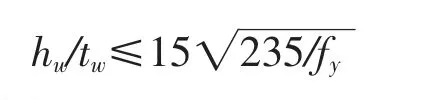
3 蜂窝梁的应用

以内蒙某项目的总调度楼为实例说明。本工程抗震设防烈度为6 度， 设计基本地震加速度值0.05 g，设计地震分组为第一组，场地类别为Ⅱ类。 该结构框架，共2 层，长57.8 m，宽21 m，控制中心上部为局部大空间，长36 m，宽18 m。

3.1 当量实腹梁截面估算

根据《钢结构设计标准》附录A 的规定，楼盖主梁的挠度允许值为［v］=17 560×（1/400）=43.9 mm，其挠度增大系数取为η=1.4，所需当量实腹梁的截面惯性矩为：

按挠度技术的最小梁高：

选取当量实腹梁截面高度为1 300 mm。

3.2 蜂窝梁切割前型钢截面的确定

蜂窝梁的扩大比，一般在1.2～1.7。由上可知其切割前的高度为800～1 100 mm，初选H 型钢尺寸为H900×300×16×28。

3.3 蜂窝梁孔型尺寸的确定及限值

蜂窝梁采用六角形如图2 所示，则其相应的尺寸为：

图2 蜂窝梁的尺寸

3.4 蜂窝梁的计算结果

在不同的扩大比下，蜂窝梁的计算结果见表1。

表1 蜂窝梁计算结果

通过表1 可发现，随着扩大比的增大，孔洞桥址处T 形截面的最大应力逐渐增大， 钢材的性能越能充分的发挥。 扩大比在1.5 附近，蜂窝梁的挠度为最小，此时的应力比为0.78，此时的蜂窝梁有将近20%的富余量，因此扩大比在1.5 附近时最为合理。

3.5 蜂窝梁的构造要求

（1）在有开孔的翼板处，无论上下，均不应有集中荷载作用；如果这种情况无法回避，可以直接填充和密封腹板上的孔洞，将该处深化为实腹梁。

（2）当蜂窝梁的实心腹板部分有集中载荷时，其结构要求可与典型的实心腹板梁相同。 即添加加劲肋。 如不能设置加劲肋时，需要对有集中荷载作用的腹板进行承载力验算。

4 蜂窝梁与其他方案的比较

（1）与混凝土梁相比：蜂窝梁截面小，自重轻，因为在蜂窝梁上做压型钢板组合楼板， 一方面可以不用支模板，施工简单，周期缩短，另一方面可以使整个屋面结构形成一个整体，大大增加其抗震性能。

（2）与实腹钢梁相比：在承载力相同的情况下，蜂窝梁比实腹梁相比， 节省钢材0.92 t， 约占17.7%。 同样在吊顶时不需用再预留其他空间。

（3）与桁架相比：桁架制作复杂，施工周期长，防腐除锈费用较高， 而且桁架一般适用于较大跨度（18～36 m），对于本工程来说，如果用18 m 跨桁架，由于钢屋架一般比较高，18 m 跨最高处达2.9 m， 采用钢屋架势必会增加层高，这一般是工程所不允许的。

5 蜂窝梁应用总结

（1）蜂窝梁截面小，承载力大，制作简单，施工周期短， 腹板处的孔洞允许管道系统与设备穿过，可以降低建筑层高，大大降低建筑造价。

（2）在有局部大空间的混凝土框架结构中，完全可以用蜂窝梁替代混凝土梁。

（3）通过几个工程的设计，对于20 m 跨度以内的结构，蜂窝梁都可以使用，达到一定的经济效果。