基坑支撑轴力不同计算方法分析

邵欣，张其立，戴东东

（1.浙江省交通运输科学研究院，浙江 杭州 311305 2.浙江勤业建工集团有限公司，浙江 绍兴 312030 3.安徽皖通高速公路股份有限公司滁州管理处，安徽 滁州 239000）

0 引言

随着地下空间的开发，深基坑工程日益增多，深基坑工程具有深度深、开挖面积大等特点。 目前对多支撑支护结构的计算方法很多， 一般有等值梁法、逐层开挖支撑力不变法、弹性地基梁法、有限元法，但这些方法计算的结果不尽相同，甚至相差很大。

谢猛等[1]研究了等值梁法在深基坑支护结构设计中的应用。 章丹峰[2]等研究了基坑监测中混凝土支撑轴力的测量影响因素与计算方法。 胡荣光等[3]考虑地下水渗流作用，进行了有限元数值建模， 得到了围护桩入土深度和钢支撑预加轴力对桩身内力及变形特性的影响规律。 等值梁法能解决土的强度问题，但无法计算变形问题。 目前，对于哪种方法更适用于工程设计，尚未得出结论。

1 分析方法

1.1 等值梁法

等值梁法的原理是假定墙后土体处于朗肯主动状态， 基坑底部以下墙前土体处于朗肯被动状态， 把基坑底面下桩底土压力零点与桩顶之间的部分当作多跨连续梁，(支撑)点位置为连续梁的支点， 采用结构力学中力矩分配法计算连续梁的方法计算支点反力，计算简图如图1 所示。

图1 等值梁法计算

等值梁法的计算步骤如下：

（1）计算作用于桩(墙)身上的土压力强度，并绘出土压力分布图。

（2）第i 层土底、顶处的主动土压力强度和被动土压力强度采用朗肯理论值。

（3）根据土压力强度值等于零确定反弯点的位置，并计算其离挖土面的距离μ，计算公式如式（1）所示。

将支护桩简化成连续梁， 其荷载为土压力，将连续梁第一段看成悬臂， 中间支锚各段为两端固定，最后一段土压力零点处看成铰支，根据《建筑结构静力计算手册》， 运用结构力学的计算方法计算固端弯矩。

（4）用弯矩分配法平衡支点弯矩并分段计算各支点反力。

（5）计算桩墙最小入土深度。

1.2 逐层开挖支撑力不变法

采用逐层开挖支撑力不变法计算时， 应根据实际施工情况， 按每层支撑受力后不因下阶段支撑及开挖而改变数值的假定进行， 即假定支撑荷载不变，支撑位移不变。 在计算每层支撑时，取下层支撑所需开挖深度进行支撑计算。 逐层开挖支撑力不变法计算简图如图2 所示。

图2 逐层开挖支撑力不变法计算

逐层开挖支撑力不变法计算步骤如下：

（1）根据各土层物理力学参数，求出围护桩墙后所受的土压力强度值及第i 层支撑时土压力零点和基坑底部的距离μi。

（2）第i 层支撑力可按第i+1 层支撑设置后挖土深度下的反弯点以上各力对该点力矩之和为零确定，在此仍然以土压力等于零的点为反弯点，第i层支撑力Ti计算如式（2）所示。

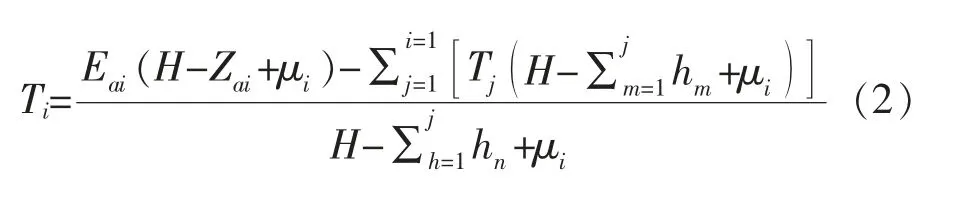
（4）在剪力为零处求最大弯矩。

2 工程实例分析

2.1 工程概况

某工程与地铁1 号线出口无缝对接。总用地面积68 085.2㎡，设三层地下室。场地周边环境复杂，市政管线较多，基坑采用双排钻孔灌注桩+地下连续墙， 结合三道钢筋混凝土内支撑的围护结构方案，桩间设三轴水泥搅拌桩挡土止水，三道支撑距地 表 分 别 为1.9 m、6.65 m、11.30 m； 基 坑 深 度15.20 m，地下连续墙嵌固深度18.5 m。地面荷载为30 kN/m2。

2.2 按等值梁法计算

本工程建筑基坑范围内成层土居多，采用分层计算土压力再逐层累加。 根据土质条件计算，开挖至15.20 m 时土压力计算结果见图3。

图3 土压力分布

土压力零点距离基坑底面距离μ=1.4 m。用弯矩分配法平衡支点弯矩， 分段计算各支点反力可得：T1=974 kN，T2=2 559 kN，T3=4 319 kN，QF=216.3 kN。最大弯矩：Mmax=642.8 kN·m。

2.3 按逐层开挖支撑力不变法计算

第一层支撑设在地面以下-1.9 m 处， 基坑开挖至-7.05 m； 第二层支撑设在地面以下-6.65 m处，基坑开挖至-11.95 m；第三层支撑设在地面以下-11.30 m 处，基坑开挖至-15.20 m。 运用朗肯土压力理论计算土压力分布， 不同工况下土压力分布如图4 所示。

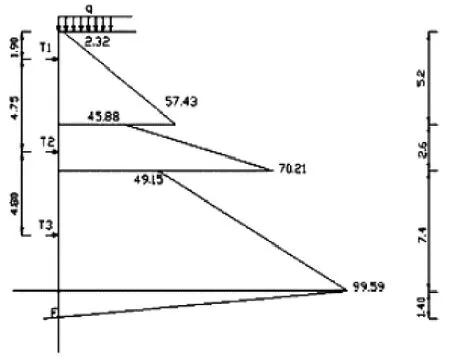
图4 土压力分布

由∑MF=0 得：T1=1 388.6 kN； 同理可得T2=2 428.8 kN，T3=3 342.2 kN，QF=186.04 kN。

可以看出两种计算方法得出的桩入土深度相差不大。

3 内力对比分析

采用理正软件的弹性法、等值梁法、逐层开挖支撑力不变法和实测数值对支撑轴力、内力进行分析。支撑轴力结果如表1 所示，内力结果如表2 所示。

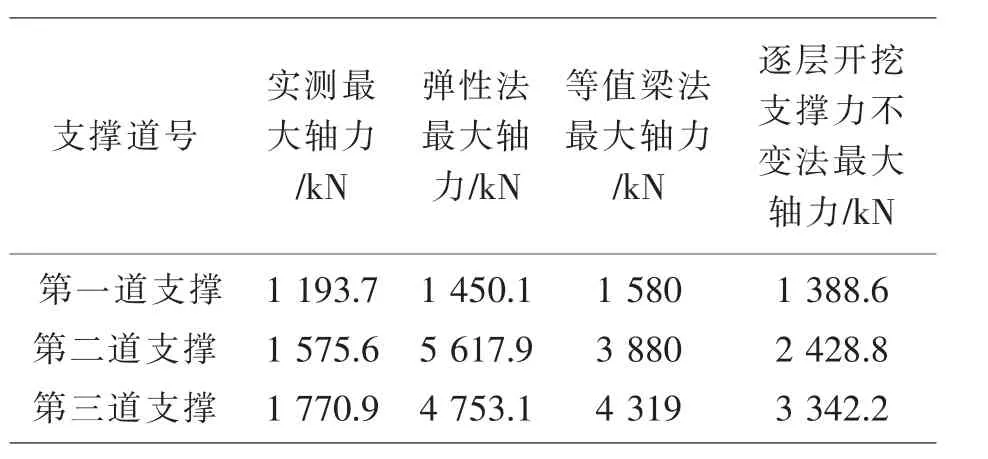
表1 三种方法计算最大支撑轴力

表2 三种计算方法支撑内力对比

由表1 可知，在支反力计算中，第一道支撑最大轴力值弹性法相对于等值梁法较小， 等值梁法和逐层开挖支撑力不变法计算的第二、 三道支撑最大轴力值处于弹性法和实测值之间， 第二道支撑最大轴力值弹性法相对于等值梁法大45.8%，第三道支撑最大轴力值弹性法相对于等值梁法大10.1%，逐层开挖支撑力不变法计算的支撑最大轴力与实测值最为接近。

由表2 可知， 最大弯矩弹性法较等值梁法大35.5%，比逐层开挖支撑力不变法大64.8%；最大剪力弹性法是等值梁法的2.25 倍， 是逐层开挖支撑力不变法的2.6 倍。 最大弯矩等值梁法比逐层开挖支撑力不变法大21.7%，最大剪力等值梁法比逐层开挖支撑力不变法大16.3%。

综上所述， 在进行深基坑支护体系设计时，基坑内侧最大弯矩、 最大剪力按照弹性法进行计算，支撑轴力按照等值梁法计算，这样更加合理。

4 结语

通过结果的对比，逐层开挖支撑力不变法与实测值相比误差较大， 在工程中适合做粗略的计算。在弹性法和等值梁法的对比中， 弹性法的最大弯矩、最大剪力比等值梁法大，各道支撑轴力值变化趋势与等值梁法更为符合，所以在进行深基坑支护体系设计时，基坑内侧最大弯矩、最大剪力按照弹性法进行计算， 而支撑轴力按照等值梁法计算，这样更加合理。