基于波动率分解与Poisson跳跃的期权定价模型研究

吴晓伟

(福建仰恩大学 经济学院， 福建 泉州 362014)

一、引言

近年来，我国资本市场飞速发展，金融创新成为衡量金融市场发达程度的重要标准，金融衍生产品的地位也越发凸显。党的十九大报告中强调了加强监管防范化解系统性金融风险的重要性。金融衍生品作为重要的避险工具，在资本市场风险管理中发挥了不可替代的作用。2015年2月9日，上海证券交易所挂牌了上证50ETF期权，意味着我国金融衍生市场交易机制进一步完善，交易频率更加活跃，丰富了投资者风险对冲工具。期权作为一种非线性衍生工具，在投资组合管理和动态对冲等领域应用广泛，是当今衍生品市场交易种类及规模位居前列的品种之一。期权研究中最关注的问题是期权能否被精确地定价，这关系到投资组合头寸对冲及后续相关交易策略实施。在金融全球一体化趋势的背景下，我国金融市场稳定不仅受到国内风险的影响，全球性金融风险的跨国传导也成了影响的重要因素，尤其是全球突发性事件如中美贸易冲突、疫情冲击等，对我国金融市场的稳定健康发展形成了挑战。突发性事件的爆发，会引起资产价格的非连续变化，降低了传统期权定价模型的有效性和准确性。因此，本文同时基于波动率分解与Poisson跳跃构建期权定价模型，对投资者改进期权交易策略、提高风险管理能力至关重要。

Black和Scholes在完全市场基础上，提出了经典的期权定价模型——BS模型，该模型可以得到欧式看涨、看跌期权的显示解。[1]但由于其假设过于严格(基础资产价格严格服从几何布朗运动，波动率和无风险利率为常数，无交易税收等)，甚至严重偏离实际，限制了BS模型在期权交易中的运用。事实上，Cont等指出真实金融市场是非完全市场，市场是有摩擦的，风险资产价格路径并非总是连续的，当发生金融危机时，资产价格往往会出现陡然地减少，即发生跳跃。[2]标的资产价格建模时如果不考虑跳跃，相应地期权定价模型在极端情况下也会产生较大偏误。而现有的市场模型大多是基于布朗运动构造的随机过程，依赖于正态分布的布朗运动无法描述极端事件发生的概率，即“黑天鹅”事件、金融危机导致资产价格出现大幅跳跃，其收益率分布具有厚尾特征。因此，为了更好地刻画真实金融市场中风险资产价格行为和提高极端事件发生的概率，不少学者将研究热点转向构造跳跃扩散过程的期权定价模型。

Merton首先将泊松跳引入到几何布朗运动中，构造了跳跃扩散过程的市场模型——默顿模型(Merton Model)，[3]该模型也是期权定价中的经典模型之一。但是，默顿模型中描述跳跃强度的参数为常数，不符合真实市场中跳跃强度具有时变性的特点。Yang等采用复合泊松过程刻画股价跳跃，其跳跃强度随时间而发生变化，进而拓展了Merton期权定价模型。他们研究表明，基于复合泊松过程的期权定价模型在定价精度上显著优于Merton-期权定价模型。[4]Peter等采用非参数估计方法，校准了跳跃扩散过程的期权定价模型，其研究表明，相对于采用参数估计的随机波动率期权定价模型，非参数模型在定价精度上更高。[5]Scott认为BS模型中利率为常数的假设不适用于短期资产定价，他采用了波动率与利率的混合随机过程，构造了变波动率-利率跳跃扩散期权定价模型，相较于利率为常数的期权定价模型，该模型在短期定价中展现了最高的预测精度。[6]Schweizer基于半鞅过程提出了半鞅期权定价模型，该模型通过引入短期债券利率以刻画利率短期期限结构变化，基于此的期权定价模型在短期内定价结果较常利率期权定价模型有更高的拟合能力。[7]Sun等研究发现，Heston模型并不能捕捉波动率微笑现象，Heston-期权定价模型在预测上有较大偏误。为了更好地拟合波动率微笑，Sun等构造了随机波动率双跳跃扩散期权定价模型，实证研究表明新模型在定价和动态对冲上显著优于Heston-期权定价模型。[8]

我国学者也对期权定价问题进行了深入研究。周仁才将基础资产波动率分解为受到两个不相关风险源影响的成分，实证研究发现其构建的基于波动率分解的期权定价模型在短期内较单因素随机波动率期权定价模型更能捕捉波动率微笑现象，因此定价精度也更高。[9]孙有发等则探讨了股灾期间上证指数对期权定价的影响，他们通过引入表征大盘指数宽幅震荡的欠阻尼二阶系统阶跃响应函数，在风险中性测度下得到了期权定价的偏微分方程(PDE)，并利用蒙特卡洛模拟得到了上证50ETF期权定价的数值解。[10]

上述研究从多角度不断改进期权定价模型，使得期权定价理论得到了长足的发展。但是，少有研究从波动率分解和跳跃两个角度同时改进标的资产价格及波动率随机过程。本文在模型中结合上述两种方法，使得突发性事件风险频发下的期权定价更加准确，这对于推动我国期权市场机制完善和发展，加强金融风险防范和化解能力具有重要意义。本文借鉴周仁才[9]和Yang等[3]研究方法，在后续研究中首先将波动率分解为受到系统性风险的整体风险源和非系统性风险[11-13]的异质风险源影响的两个成分，并在资产价格随机微分方程(SDE)中引入了两类风险源共同引起的泊松跳跃过程，然后在风险中性测度下推导了该过程的期权定价PDE。最后，采用蒙特卡洛模拟得到期权定价PDE在欧式期权条件下的数值解，并结合多种损失函数评价波动率分解期权定价模型和新模型的定价能力。

二、模型构建及期权定价PDE

在真实金融市场上，由于交易双方需求的多样性和复杂性，造成风险资产定价的风险来源存在很大不同。比如，对于股票定价而言，系统性风险来源于股票市场整体情绪，非系统性风险(异质风险)往往是特定交易者(机构投资者)的异常交易(内幕交易、非正常大宗交易等)行为引起。因此，区分风险源对于资产定价而言十分重要。借鉴周仁才[9]研究思路，下面考虑引入这两类风险源及共同引起的跳跃对数资产价格及波动率随机过程：

利用Ito积分可以得到相应股价随机微分方程(SDE)形式为：

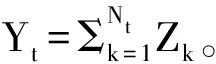
根据风险中性定价原理，股价贴现过程是鞅。因此在风险中性测度下，股价和波动率满足的随机微分方程为：

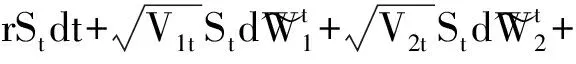
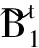
Heston等认为实际金融市场上的波动率具有均值回复、波动聚集、跳跃等特点，而历史波动率模型(GARCH族模型)虽然可以很好刻画均值回复特点，但是明显低估了波动率的跳跃幅度。因此，他提出了基于CIR过程的随机波动率模型以更好地解决在资产价格出现跳跃时的期权定价问题。[16]CIR过程[17]采用均值回复的平方根刻画波动率在长期预测中的变化，而该过程可以得到欧式期权的封闭解。在风险中性测度下，系统性风险源和非系统性风险源满足的SDE如下：

其中，λ1,λ2,ξ1,ξ2,σ1,σ2均为常数，ρ1,ρ2也均为常数。对比上式可以看出，φ1=-λ1ξ1，φ2=-λ2ξ2，因此波动率长期均值可以表示为λ和ξ的线性组合。当令b=-λ1ξ1,n=-λ2ξ2时，我们可以进一步简化f(t,v,w,x)服从的PDE：

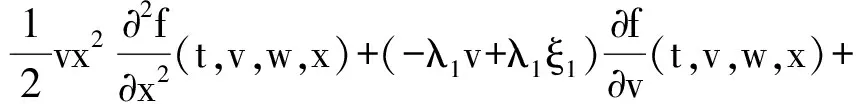
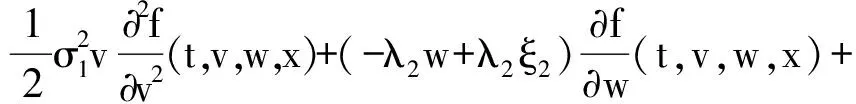
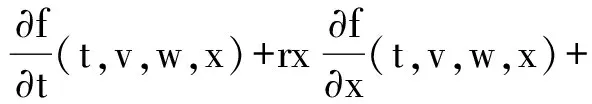
一般而言，上述PDE不存在解析解。若不考虑跳跃过程，则模型退化为周仁才提出的基于波动率分解的期权定价模型。[9]为了进一步简化PDE，我们令，目的是消去PDE中关于跳跃的数学期望，将复合泊松跳过程退化为泊松跳过程，这样便于进行参数估计和简化蒙特卡洛模拟[18，19]时的数值计算。简化的PDE形式如下：

三、实证研究

期权作为一种非线性衍生工具，相较于期货定价，波动率在定价过程中的作用十分重要。要评判期权定价模型的优劣，一种常用的方法是采用多种损失函数对比模型拟合价格和真实交易价格的误差；另一种方法是采用损失函数比较波动率模型及隐含波动率的拟合偏误。本节分为两部分，一部分借鉴Corsi等[20]研究方法，采用RMSE(均方根误差)比较波动率分解期权定价模型(HVOP Model)和基于波动率分解和泊松跳跃的期权定价模型(VJDOP Model)拟合隐含波动率(IV)的精度，第二部分将沿用主流研究方法，将HVOP模型及VJDOP模型拟合值和交易价格进行比较，并结合HMSE、RSME、HMAE三种损失函数对模型拟合能力做出更加严谨的评判。

1.拟合隐含波动率

Mesias等指出Heston模型并不能较好拟合短期隐含波动率微笑现象，因为资产价格在短期内跳跃频繁，Heston-期权定价模型在短期期权定价中存在较大预测偏误。[21]基于此，本文在资产价格随机微分方程中引入泊松跳，并将随机波动率按照系统性风险源和非系统性风险源进行分解，分解后的波动率随机微分方程借鉴Heston模型中采用的均值回复过程，以提高期权定价模型短期拟合能力。

Heston模型参数估计流程较为复杂，本文采用模拟退火算法估计Heston模型参数。模拟退火算法具有较高的稳健性和鲁棒性，可避免局部最优陷阱，其估计参数的结果较快收敛于全局最优解[22，23]。借鉴周仁才[9]研究结果，给定参数向量的初始值Λ0=(λ1,ξ1,ν1,σ1,ρ1,λ2,ξ2,ν2,σ2,ρ2)=(0.04,0.75,0.13,0.26,-0.2,0.05,0.8,0.18,0.24,-0.2)，期权样本选择上证50ETF 2019年9月到期，执行价为2.50-3.20元的认购期权(共计13份合约)，这是因为期权市场交易4年以来，当月及季月合约往往是对冲的主力合约，其交易量大，流动性好，再考虑到季月合约交易数据远多于当月合约，可以增加拟合定价的样本数，因此本文选择季月合约。无风险利率采用一年期上海银行间同业拆借利率rf=3.084%，α=1.67。为了更加直观地反映基础资产在期权有效期内的走势，图1是这期间上证50ETF时序图。

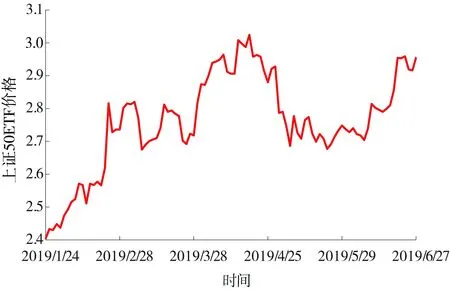
图1 上证50ETF时序图

从图1不难看出上证50ETF走势在2019年2月和5月发生了两次较为明显的月线级别的暴涨暴跌，这是因为受到中美贸易摩擦的影响，资产价格发生了大幅跳跃，且跳跃具有较强的持续性。从周线级别看，短期内上证50ETF价格出现跳跃次数更为频繁。因此，在基础资产价格的SDE中引入跳跃过程十分必要，本文构建的基于波动率分解和泊松跳跃期权定价模型符合样本走势特点，其经济意义显著，具有一定的研究价值。为了后续研究的展开，表1给出了波动率分解模型的参数估计结果。

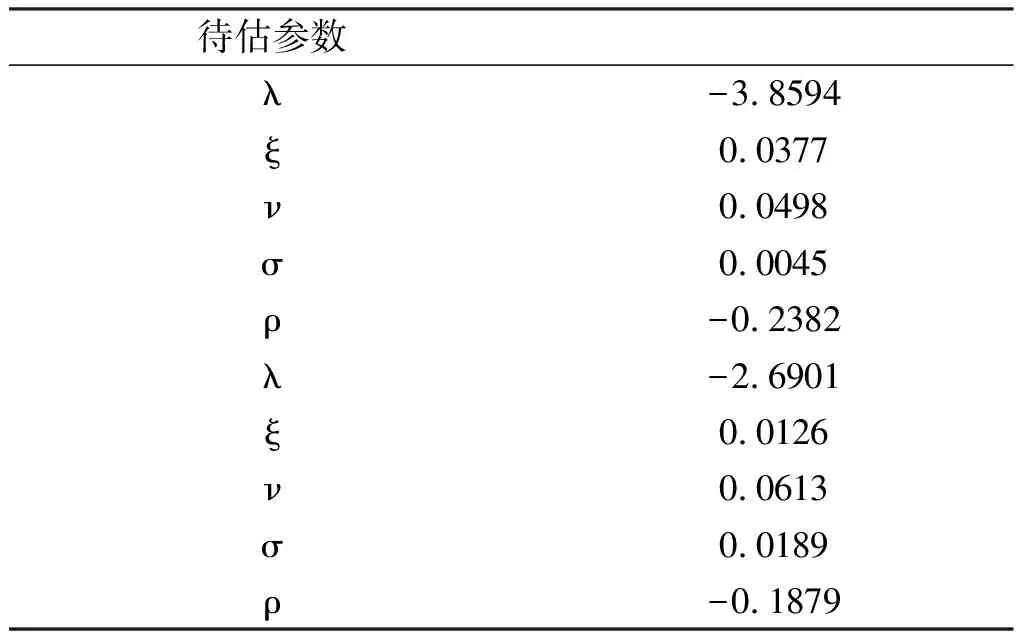
表1 模型参数估计结果

由表1可看出，基于波动率分解的波动率模型两个风险源长期均值分别为φ1=-λ1ξ1=3.8594*0.0377=0.1455,φ2=-λ2ξ2=2.6901*0.0126=0.0339，这表明波动率两个风险源均值差异较大，资产价格风险往往来源于多重因素(经济环境变化、公众预期等)，且每个因素对波动率的影响程度不同，周仁才[9]提出的波动率分解模型具有较明显的经济意义。从相关系数角度看，两个风险源均与上证50ETF走势负相关，这也符合波动率与标的资产价格走势往往具有负相关的市场现象[24]。为了更加直观看出HVOP和VJDOP模型对隐含波动率的拟合能力，图2给出了两模型在不同剩余期限，对不同执行价的认购期权隐含波动率拟合图。

由图2可知，隐含波动率存在明显的倾斜效应，这说明上证50ETF期权隐含波动率也具有波动率微笑特点，这和主流研究结果一致。[25，26]为了分析方便，黑圈表示剩余期限为90天时，市场真实的隐含波动率。蓝实线代表VJDOP模型的拟合值，红虚线代表HVOP模型的拟合值；当剩余期限为120天时，菱形代表市场真实的隐含波动率，紫实线代表VJDOP模型的拟合值，绿虚线代表HVOP模型的拟合值。

从图2我们可以看出，当剩余期限为90天时，两模型拟合能力相差不大，VJDOP模型拟合能力略优于HVOP模型。当剩余期限为120天时，两模型拟合能力出现较为明显分化，尤其是对于实值期权而言，VJDOP模型拟合能力显著优于HVOP模型。当执行价为2.8元时，两模型拟合偏误均达到最大，这是因为此时期权状态接近平值，处在实虚值状态转换的关键时刻，交易双方对未来波动率走势存在明显分歧导致模型拟合偏误增大。

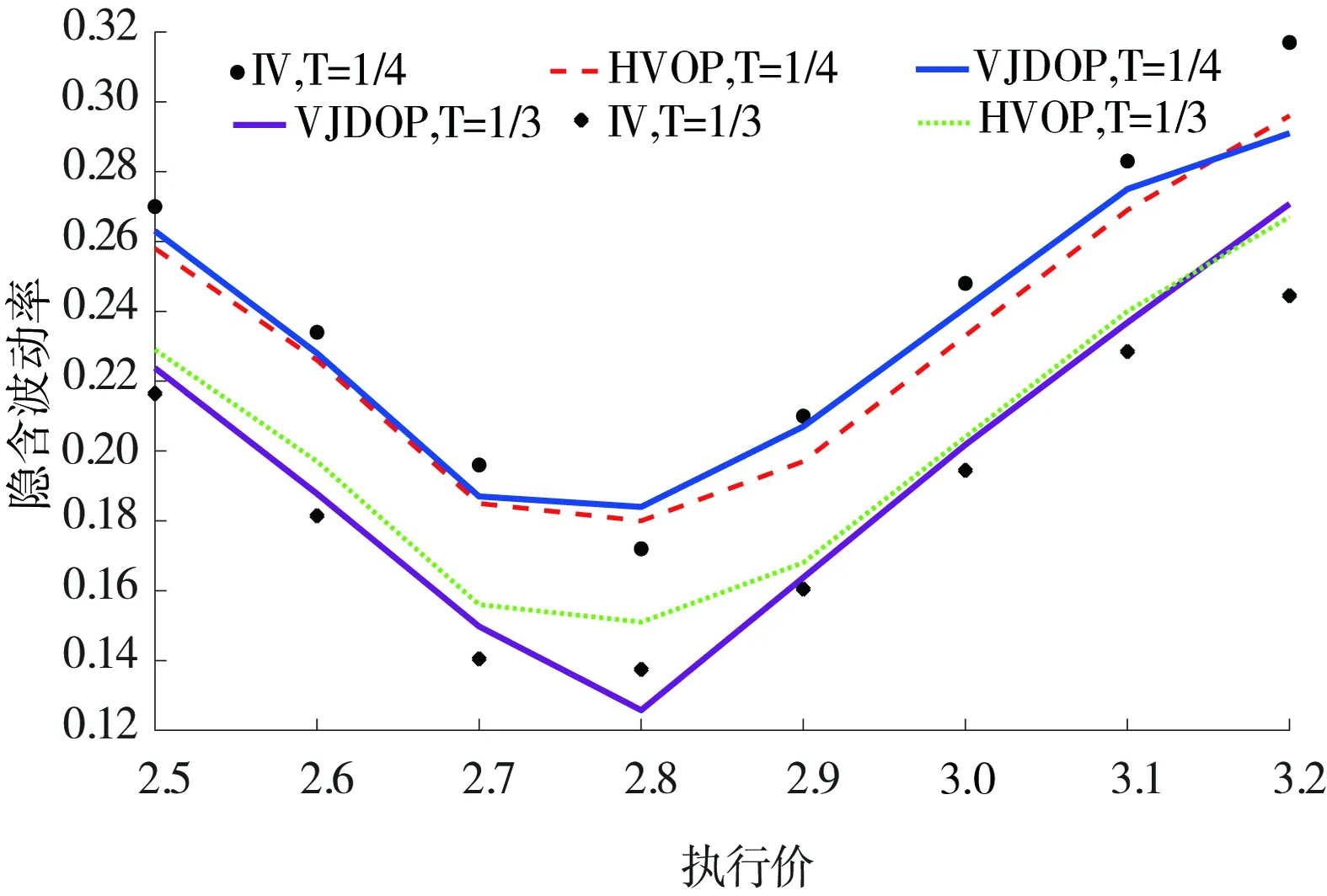
图2 各模型隐含波动率拟合图

为了得到更为严谨的结论，下面采用RMSE损失函数对HVOP模型和VJDOP模型的拟合能力做出更加科学的评判。Corsi等[20]定义隐含波动率的RMSE损失函数表达式如下：

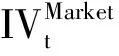
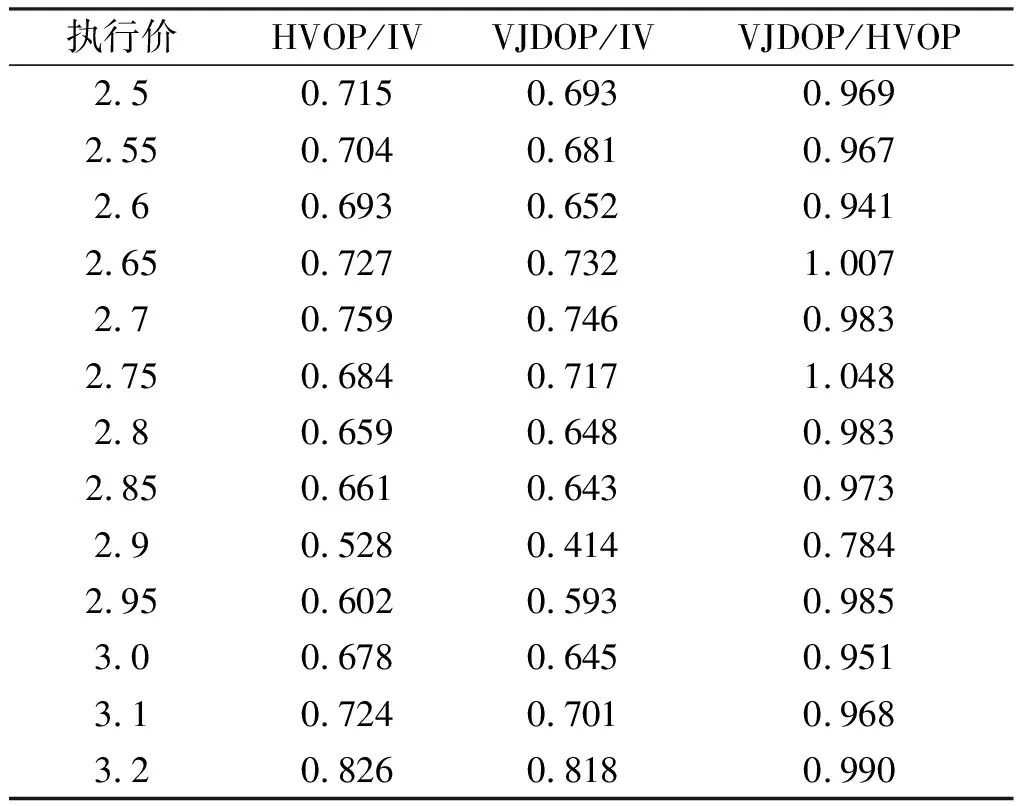
表2 HVOP、VJDOP模型拟合值与隐含波动率的RMSE比值(T=1/3)

由表2可知，除了在执行价为2.65元和2.75元时，HVOP模型拟合能力优于VJDOP模型外，在其他情况下，VJDOP模型优于HVOP模型。总体来看，当执行价略高于2.9元时，VJDOP模型RMSE与HVOP模型RMSE比值更小于1，表明VJDOP模型对虚值期权隐含波动率拟合能力优于实值期权，随着执行价继续提高，变为3.2元时，两模型比值0.99，JVDOP模型拟合能力略高于HVOP模型，这说明在拟合深度虚值期权隐含波动率上，HVOP模型和VJDOP模型拟合精度相差不大，VJDOP模型更适合拟合虚值期权的隐含波动率。

以上研究从拟合隐含波动率角度，对比了波动率分解期权定价模型及波动率分解和泊松跳跃期权定价模型的拟合精度，无论是从直观上看(图1)还是采用RMSE损失函数做出更加科学的判断(表2)，结果发现VJDOP模型在绝大多数执行价下拟合能力要优于HVOP模型，一方面，在短期内，标的资产价格出现跳跃在真实金融市场上是广泛存在的，如果建模时未加入跳跃因素，对于短期定价而言，模型必然会产生偏误。正是VJDOP模型加入了泊松跳，能够很好捕捉样本特点，其拟合能力才会优于不带跳跃的波动率分解期权定价模型。另一方面，隐含波动率作为反映交易价格的代理变量，模型是否精准拟合隐含波动率是模型评价中的重要部分。

尽管如此，现阶段主流的评价体系还是直接比较期权定价模型拟合结果与真实交易价格的偏差，因此，为了使得结论更有说服力，本文将结合三种损失函数进一步评价HVOP模型与VJDOP模型的拟合能力。

2.拟合交易价格

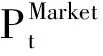
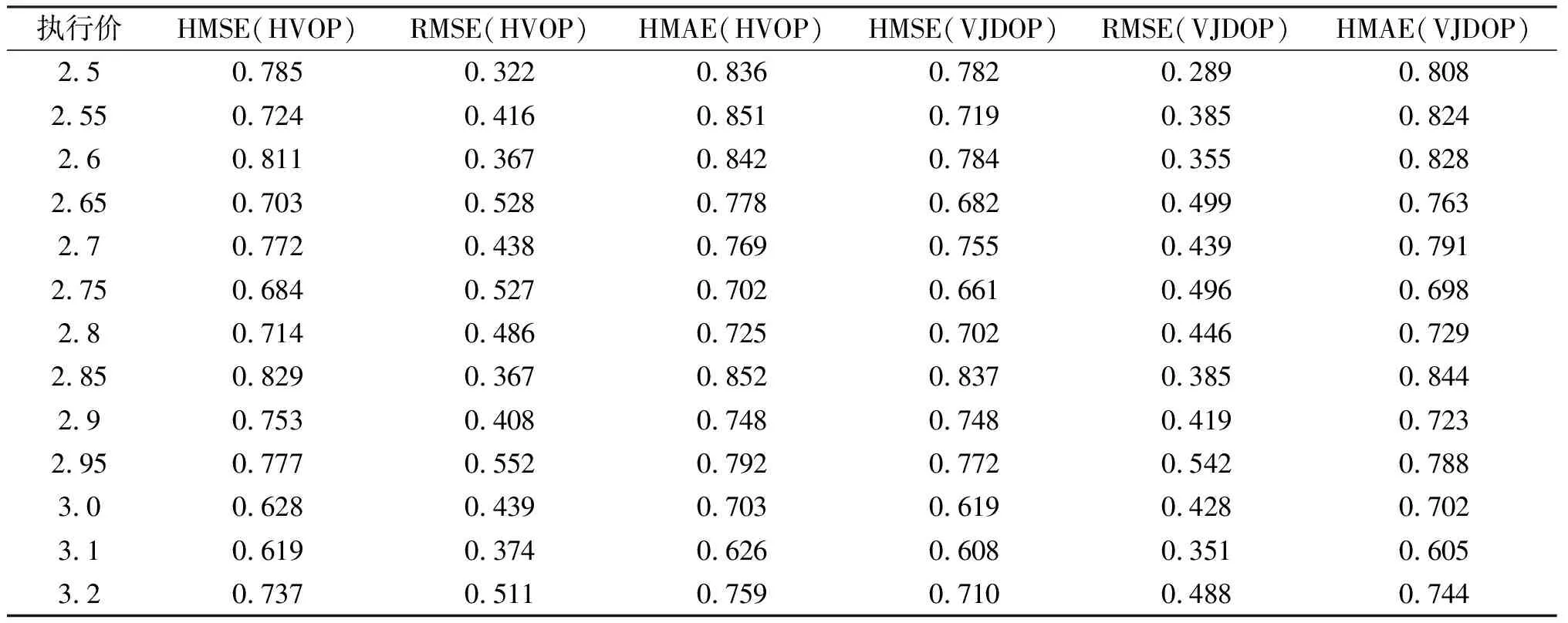
表3 HVOP、VJDOP模型拟合交易价格损失函数值(9月到期)

由表3可知，除了标黑部分外，其余损失函数值均是VJDOP模型较HVOP模型要小。对应于执行价为2.7、2.8、2.85、2.9元的期权，VJDOP模型较HVOP明显并非有显著的定价优势，但在其他执行价下，VJDOP模型通过了所有损失函数的检验，定价准确率为70%。从VJDOP模型定价误差较大的期权来看，此时期权执行价为2.8-2.9元时，标的资产价格正好也处在这一范围，因此这些期权是平值期权。如前所述，在拟合隐含波动率时，平值期权交易双方对未来波动率走势存在较大分歧，两模型拟合平值期权的隐含波动率也存在较大偏误，而表3数据也表明，这样的误差也会反应在定价上，造成VJDOP模型定价优势较HVOP模型并不明显，甚至定价效果更差。当期权处于实值或者虚值状态时，从这三种类型损失函数判断，VJDOP模型定价精度显著优于HVOP模型，说明考虑了短期资产价格跳跃因素(见图1)，使得VJDOP模型更能捕捉样本特点，其定价精度较忽视基础资产在短期内发生跳跃的波动率分解期权定价模型更高。

四、结论

期权作为一类重要的金融衍生品，在风险对冲和投资组合头寸管理等领域应用广泛。其中，期权定价问题是学界和实务界最为关注的问题之一，因为期权定价准确与否会影响到投资组合绩效和后续交易策略实施，因此，不断改进期权定价模型，提高模型定价能力是学术界研究的一大热点。20世纪70年代，Black和Scholes[1]提出的经典期权定价模型——BS模型只需要5个易得的市场变量，即可求得期权价格。该模型对于欧式期权具有显示解，因此应用十分广泛。但是，基础资产价格服从几何布朗运动的假设使得BS模型无法精确刻画短期内基础资产价格的大幅跳跃，如何引入合适地跳跃过程，提高模型拟合能力成了后续研究热点。

Merton率先用Poisson过程作为基础资产价格的跳跃过程，构造了漂移扩散的几何布朗运动随机微分方程，并结合BS公式得到了欧式期权的解析解。[3]借鉴Merton[3]的研究方法，本文在周仁才[9]提出的波动率分解期权定价模型基础上，实证研究发现：

第一，波动率分解模型的两类风险源——系统性风险与非系统性风险引起的波动率均与标的资产价格走势呈现负相关关系，这也和Papanicolaou等[24]研究结果一致，即在模型形式设定上，基础资产价格SDE中的布朗运动与随机波动率SDE中布朗运动之间的相关系数往往为负。

第二，上证50ETF认购期权隐含波动率存在波动率微笑现象。而在拟合隐含波动率能力上，需要考虑期权所处的状态。对于实值期权，基于波动率分解和Poisson跳跃的期权定价模型(VJDOP Model)拟合能力略优于波动率分解模型(HVOP Model)；对于虚值期权，VJDOP模型拟合能力显著优于HVOP模型；而当期权处于平值状态时，两模型均表现出较大的拟合误差，这和平值期权处在实虚值状态转换节点有关，交易双方对未来波动率存在较大分歧，而量化模型无法刻画投资者行为是导致模型拟合较差的主要原因。

第三，在拟合交易价格上，对于实值与虚值期权，VJDOP模型较HVOP模型具有更高的拟合精度。而在平值期权上，VJDOP模型拟合能力比HVOP模型更差。由于隐含波动率往往反映了期权交易价格，这与VJDOP模型拟合平值期权隐含波动率效果较差这一结果相吻合。

总体来说，基于波动率分解与Poisson跳跃的期权定价模型能够更加准确地拟合隐含波动率与交易价格。尤其在“跳跃”现象普遍存在的金融衍生品市场中，突发性事件时常引起金融市场短期剧烈波动，产生波动聚集现象。如果不将“跳跃”现象纳入模型的考量中，将影响资产定价效率，本文研究的意义也在于此，通过本文研究能够为现实中的期权合理定价提供参考与借鉴。