投影系统中DMD衍射效率的研究

谷晓雁，王春艳，孙 昊，王志强，刘 欢

（1.长春理工大学 光电工程学院，吉林 长春 130022；2.江苏北方湖光光电有限公司，江苏 无锡 214000）

引言

数字微镜阵列（DMD）作为一种反射式空间调制元件，利用微镜的偏转控制光线反射方向，达到光学调制的目的，具有分辨率高、响应速度快、像素无坏点等优点[1]。将DMD 应用到投影系统中，微镜偏转的2 个角度对应3 个状态，当微镜偏转角度为+12°时为“开态”，允许反射光束进入投影系统；当微镜片偏转−12°时处于“关态”，反射光束偏离投影系统[2-4]。

DMD 作为DLP 投影系统的核心部件，主要在近红外、中波红外波段使用，长波入射时因为微镜尺寸和波长近似，因此产生的衍射效应比较大，此时会形成反、衍混合的成像特性，对投影系统的像质有很大影响[5]。本文讨论波长为7.7 μm～9.5 μm，DMD 尺寸为1.40 cm（0.55 英寸），每个微镜的尺寸为10.8 μm，入射光波长和DMD 的微镜尺寸相近，需要考虑DMD 的衍射效应，将其作为闪耀光栅进行建模分析。利用基于矢量衍射理论的严格耦合波法建立闪耀光栅模型，通过求解闪耀光栅反射区域和透射区域的电磁场表达式，最终确定衍射效率。

1 DMD 微透镜结构及特点

1.1 DMD 微透镜结构

DMD 微镜以二维阵列形式排列，其结构和成像原理决定了它是反射和衍射混合元件，工作机理是依靠作为像素的微镜的反射，遵循反射定律,又因为具有特殊的微镜结构，DMD 在客观上表现出类似二维光栅的衍射性质[6-10]。因此，需要对DMD 微镜结构的衍射光学特性进行进一步分析。由于微镜的偏转轴是对角线，每个微镜存在2 个方向的对角线。设微镜的主对角线与偏转轴平行，与之对应的另一条就是副对角线，DMD微镜在这2 个方向上的偏转都会产生衍射效应[6]。

1.2 DMD 反、衍射特性

考虑DMD 主对角线上M个微镜元处于开态时，微镜的偏转轴恰好与主对角线方向一致，此时M个微镜片均在同一平面内，相邻微镜的反射光波之间并不存在相位差。当副对角线微镜处于开态时，衍射效应与闪耀光栅类似，微镜片两两异面，相邻微镜片存在相位差，如图1所示。令DMD表面的法向量为，开态微镜片所在平面的法向量为，i为入射角，θ为反射角，γ为微镜偏转角，，w为微镜尺寸，根据反射定律可知闪耀条件为θ=2γ-i。

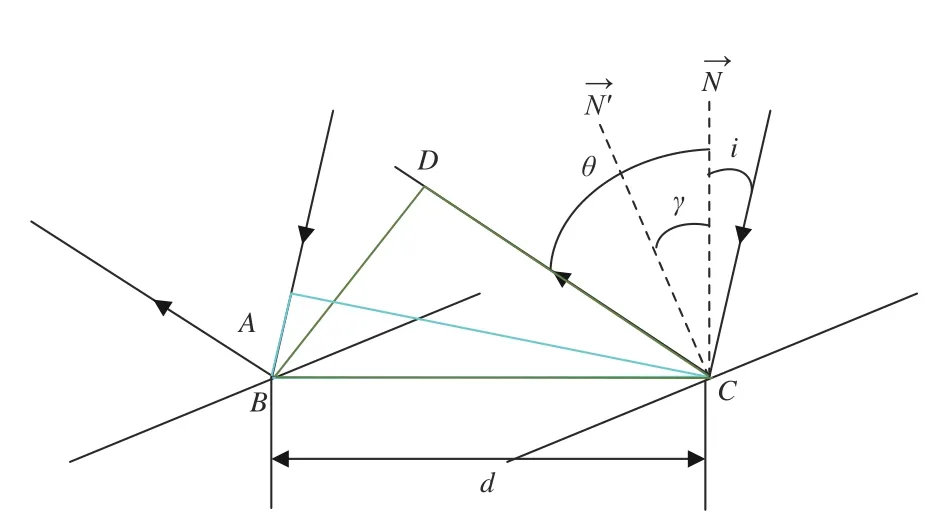
图1 反射光波相位差图Fig.1 Phase difference diagram of reflected light waves

此时两开态微镜反射光波的光程差可以表示为

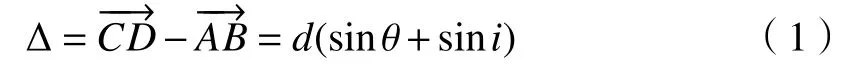
将θ=2γ-i带入上式，可得相邻两微镜反射光波相位差为

当闪耀角 γ、光栅常数d、波长 λ确定后，反射光波相位差δ仅仅和入射角度 θi有关，在闪耀角为12°，波长为0.632 5 μm、3 μm、8 μm 时反射光波的相位差随入射角度的变化规律如表1所示。

表1 不同波长下反射光波相位差随入射角的变化Table 1 Phase difference of reflected light waves varies with incident angles at different wavelengths

从相位差中(sini+sin(2γ-i))以及表1 中的数据可以看出，光程差的变化关于i=γ对称，并且入射角离 γ越远，单位入射角的调整对光程差 Δ和相位差 δ的影响越大。因此，讨论入射角度对DMD的衍射效率的影响很有必要。

2 不同入射角下衍射效率计算

2.1 DMD 闪耀光栅模型

普通光栅由于单缝衍射的零级主极大和缝间干涉的零级主极大重合，导致大部分能量集中在零级，闪耀光栅通过闪耀角使大部分能量转移到某一衍射级次上，实现该衍射能级的闪耀。闪耀级次位置会随着闪耀角变化而发生变化，数字微镜器件DMD 的微镜以对角线为轴翻转，各个微镜发生倾斜后，微镜结构就呈现闪耀光栅模型[9]，如图2所示。

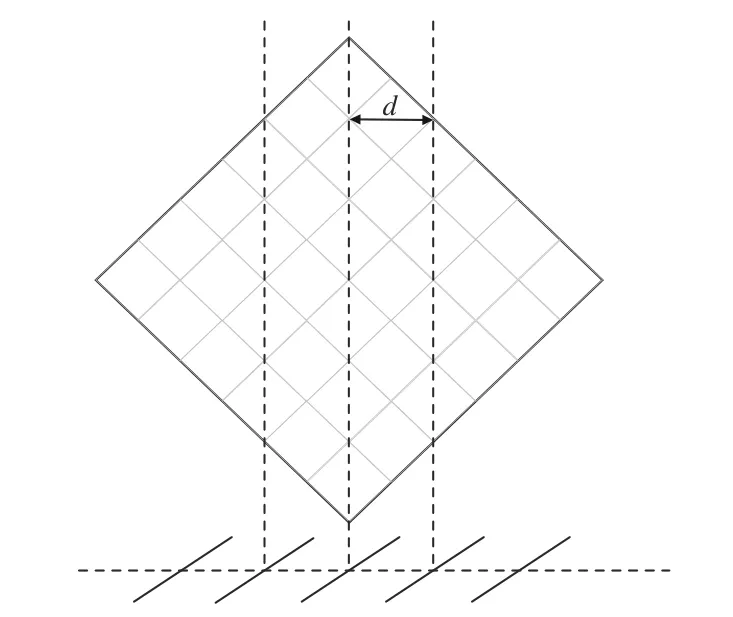
图2 DMD 闪耀光栅模型Fig.2 Schematic diagram of DMD blazed grating model

闪耀光栅模型所对应的衍射模型如下：

由闪耀方程（3）式可知，任一入射角都对应着某一个衍射级次的一个闪耀波长，DMD 微镜的闪耀角，则可以求解出在λ=7.7 μm、8 μm、9 μm、9.5 μm，入射角在0°～90°时闪耀级次随入射角的变化，如图3所示。

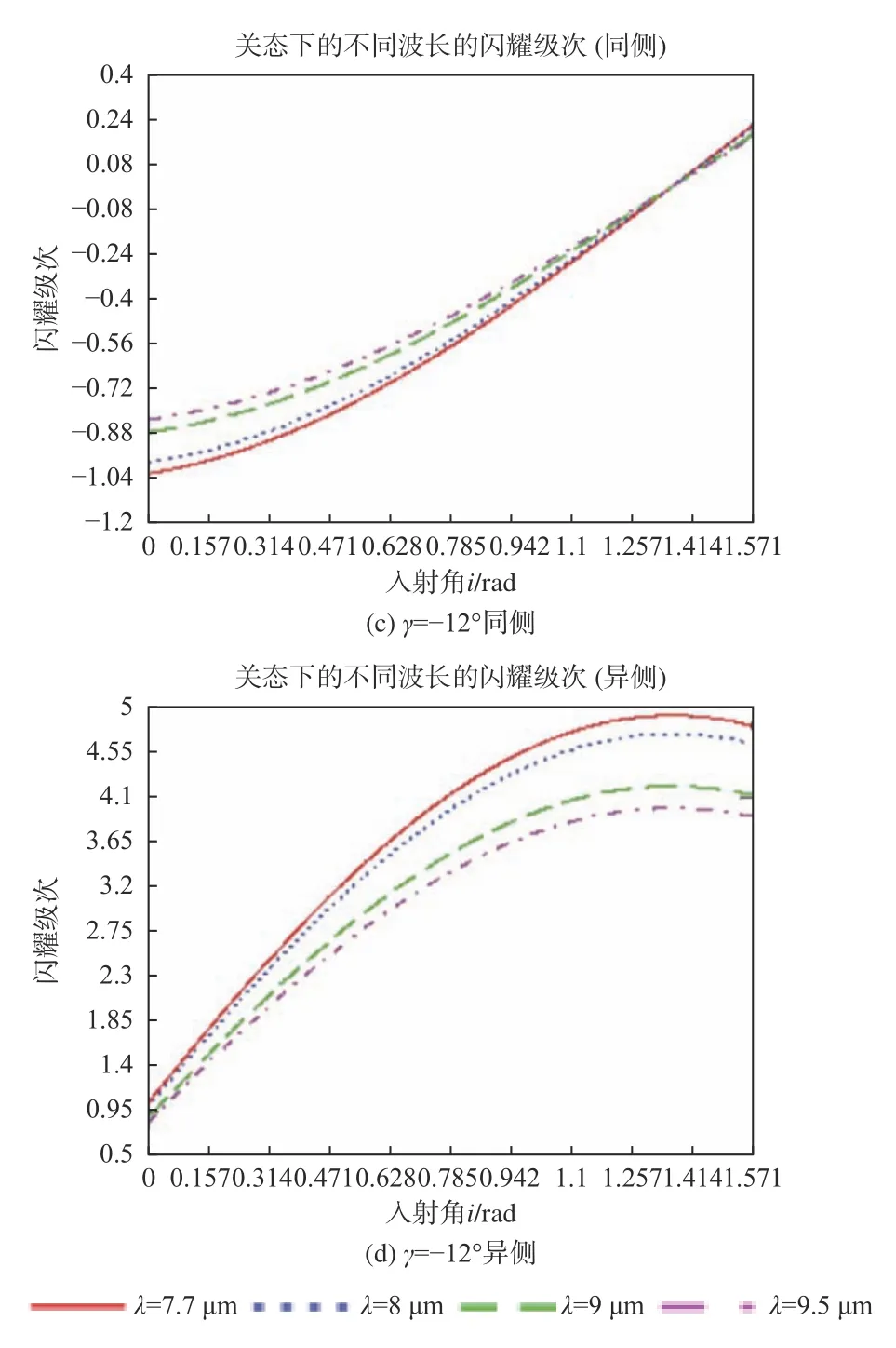
图3 闪耀级次和入射角度的关系Fig.3 Relation between blaze order and incident angle

经过计算得知，当入射光线和衍射光线异侧时，根据光栅衍射方程计算出来的衍射角大于90°，因此选择入射光线和衍射光线位于同侧时的闪耀级次。同时衍射能级必须取整数，当闪耀角γ=+12°时，闪耀级次取+1 级次；当闪耀角 γ=−12°时闪耀级次为−1 级次。

由图4 可以看出，7.7 μm～9.5 μm 长波红外所对应的闪耀级次为1 级。接下来利用矢量衍射理论计算长波红外入射到DMD 上1 级衍射级次在不同入射角度和不同偏振态的衍射效率。

图4 有效闪耀波长Fig.4 Effective blazed wavelength

2.2 衍射效率计算

利用矢量衍射理论分析不同入射角对DMD衍射特性的影响。基于闪耀光栅模型，将其划分为厚度相同的若干层矩形光栅，其占空比不同，周期相同[4]。当电场分量垂直于入射面时为TE 偏振光，磁场分量垂直于入射面时为TM 偏振光。计算空间方位角为0°时不同入射高度角的衍射效率。经过MATHCAD 软件仿真，计算不同入射角在m=1衍射能级时波长为7.7 μm、8 μm、9 μm、9.5 μm 下对应的衍射角，如表2所示。

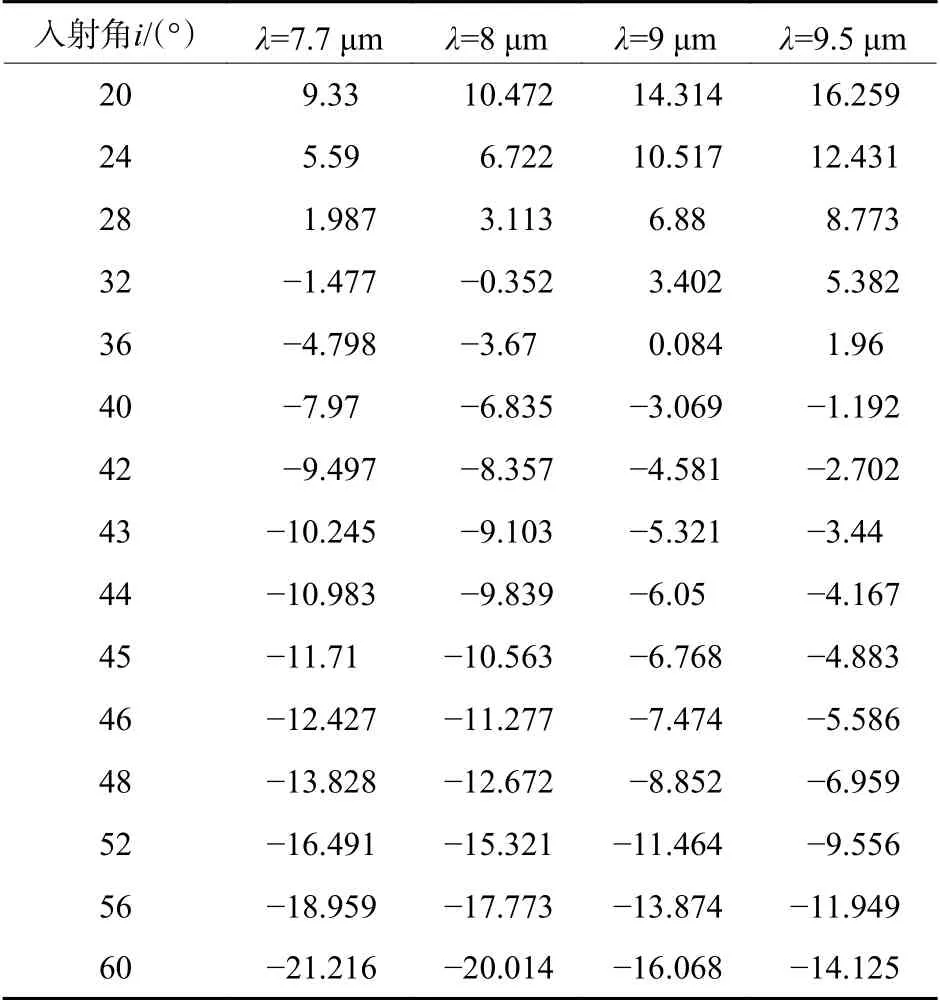
表2 不同入射角时不同波长的1 级衍射光角度Table 2 First order of diffracted light angles at different angles and wavelengths（°）

根据表2 可以得出如下结论：

1)入射光波长 λ=7.7 μm，光束入射角 θi在20°～44°范围内时，经DMD 调制后的1 级衍射光角度θr在投影系统的光束孔径角范围内；

2)入射光波长 λ=8 μm，光束入射角 θi在20°～45°范围内时，经DMD 调制后的1级衍射光角度θr在投影系统的光束孔径角范围内；

3)入射光波长 λ=9 μm，入射角 θi在24°～48°范围内时，经DMD 调制后的1 级衍射光角度 θr在投影系统的光束孔径角范围内；

4)入射光波长 λ=9.5 μm 时，入射角 θi在 28°～52°范围内时，经DMD 调制后的1 级衍射光角度θr在投影系统的光束孔径角范围内。

因此，将DMD 在7.7 μm～9.5 μm 波段应用于红外投影系统，且光束入射角 θi在28°～44°范围内时经DMD 调制后的1 级衍射光角度 θr在投影系统的光束孔径角范围内，投影系统可正常工作[11-13]。

下面分析光束偏振态对微镜衍射特性的影响。将其等效为闪耀光栅并将光栅模型划分为80 层，利用麦克斯韦方程组和电磁场的边界条件求解不同偏振光入射下各衍射级次的衍射效率[6]。TE 和TM 偏振光可独立计算且计算方法相同，只是因为TE 和TM 的电场振动方向有差异，导致求出的Rm不同。求解衍射效率公式如下：

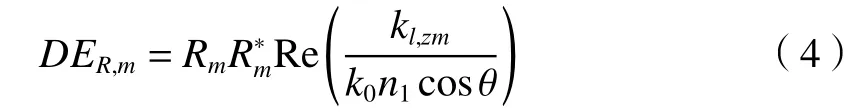
式中：m为 衍射级次；k0为真空入射光的波矢分量；n1为反射区的折射率；Rm为第m衍射级次的反射率，可由特征值法求解得到；θ为入射角；kl,zm表示光栅发现方向的波矢分量，可由下式求出：

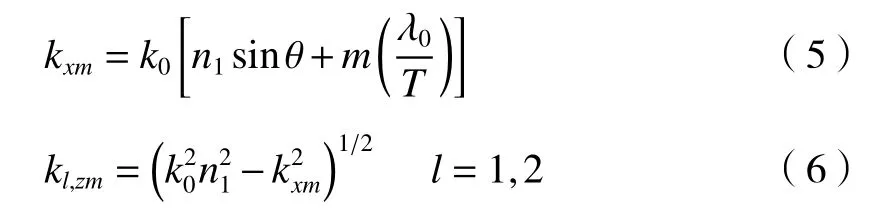
由(4)式可求出光源为TE 偏振光，入射角度在28°～44°范围内时，微镜处于全开态时的1级衍射效率在30%～40%。当光源为TM 偏振光，入射角度在24°～44°范围内时，微镜处于开态时的1 级衍射效率在55%～70%，入射角为44°时1 级衍射效率可以达到70%，关态时的1 级衍射效率为5%。因此7.7 μm～9.5 μm 波段的红外波入射到DMD上，入射光束为TM 偏振光，入射角度为44°时，进入系统的1级衍射效率最大，可以满足DMD 型目标景象生成器的要求。

将DMD 放入投影系统中，并且以黑体作为光源[14-15]，波长为7.7 μm～9.5 μm，视场为2.97°，反向设计可得到合适的投影系统。综上所述，TM 偏振光源入射角度为44°时可以得到最大的1 级衍射效率，光学系统结构如图5所示。

图5 光学系统整体结构图Fig.5 Overall structure diagram of optical system

照明光束在XZ平面内，其光轴与投影系统的光轴即Z轴成44°角，使用IR 全息线栅偏振片得到TM 偏振光。当DMD 处于开态时1 级衍射光可以进入光学系统，进入的衍射效率如图6所示。

图6 入射角为44°时TM 偏振光入射的一级衍射效率Fig.6 First order diffraction efficiency of TM polarized light incident when incident angle is 44°

3 结论

本文从DMD衍射效应分析和衍射效率计算2 个方面展开研究，将DMD 等效为二维闪耀光栅，影响长波红外波段入射到微镜上产生衍射效应的因素有波长、微镜宽度、微镜偏转角度以及入射角度。当其他条件固定时，控制入射角度可以控制衍射效应的分布，使入射角度满足闪耀条件，使能量集中在某一衍射级，入射光的偏振态对衍射级的衍射效率也有影响。通过矢量衍射理论对入射角和偏振态对衍射效率的计算，发现当照明光束为TM 偏振光，入射角度在44°开态时的1 级衍射效率达到70%。