热风熔融废旧塑料造粒机熔融室温度场分析
谭 磊,黄兴元∗,王 涵,潘留雯
(南昌大学机电工程学院,江西省轻质高强结构材料重点实验室,南昌 330031)
0 前言
塑料因其成本低、质量轻、强度高、耐腐蚀、加工方便等优异性能,被广泛应用在国民经济的各个领域。但随着塑料制品的不断使用,废旧塑料也随之与日俱增,给环境造成的污染也日趋严重。目前,废旧塑料主要的处理方法是:填埋、焚烧、再生利用等。填埋处理是一种操作简单、投资成本低的处理方法,但填埋占用土地面积,浪费土地资源[1];焚烧处理是回收利用废旧塑料燃烧时所产生的热量,但是焚烧会释放多种有害物质,如强致癌物质二恶英[2],严重危害人类健康和生态环境;再生造粒是通过造粒工艺将废旧塑料变为颗粒的回收方法,也可用于成型加工,制得的产品性能与原产品的性能相差不多,具有很高的经济价值[3]。相比于填埋处理和焚烧处理,再生造粒是真正意义上的资源再生循环利用。近年来,诸多学者对其展开了研究。周献华等[4‑5]根据新型的热风熔融造粒工艺设计出立式热风循环加热废旧塑料回收造粒实验样机,而陈丹等[6‑7]在周献华等研究基础上完成了实验研究和改进设计,证实了热风熔融造粒工艺的可行性。立式热风循环加热废旧塑料回收造粒机作为新型的塑料回收造粒机,使用新型的塑料回收造粒机工艺,即热风熔融塑料回收造粒方法。它采用热风循环加热废旧塑料,使塑料熔融,进而挤出造粒。相比于传统螺杆挤出造粒工艺,它直接加热废旧塑料,省去了粉碎、清洗、烘干等过程,减少工艺步骤,节约投资成本,加快回收。立式热风循环加热废旧塑料回收造粒实验样机结构简图如图1所示。工作原理为:废旧塑料由料斗落于熔融箱体,通过热风循环加热并在搅拌轴连续搅拌作用下加速熔融,最后通过螺杆挤出造粒,同时热风在离心风机作用下,依次通过离心风机、加热管然后进入熔融箱体,这样往复循环完成加热。
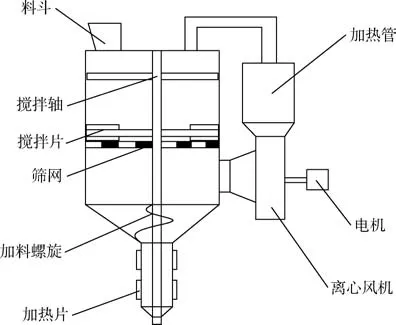
图1 立式热风循环造粒机结构图Fig.1 Structure diagram of vertical hot air circulation granulator
熔融室作为暂时存储和熔融塑料的筒体,其温度分布对熔融塑料至关重要:一方面热量集中区域,塑料吸收过多的热量,导致塑料受热分解;另一方面热量稀少区域,塑料熔融过慢,加热时间变长,工作效率变低。故本次模拟考虑在多参数的环境下,即进风口直径、进风口位置和风速等,研究熔融室温度变化、分布等,对多参数环境下的熔融室温度分布、变化获得足够的认知,并采用正交试验法,得出熔融室最优结构参数。
本文针对上述问题,对照机器,简化模型,使用Fluent软件进行模拟,分析各参数对非对称熔融室温度分布的影响,同时采用正交试验法得到熔融室最优结构参数,提供结构合理、方便可靠的优化方案,使机器能够更有效地熔融,提升造粒效率。
1 熔融室模型建立
熔融室的几何模型如图2所示,熔融室几何参数如表1所示。
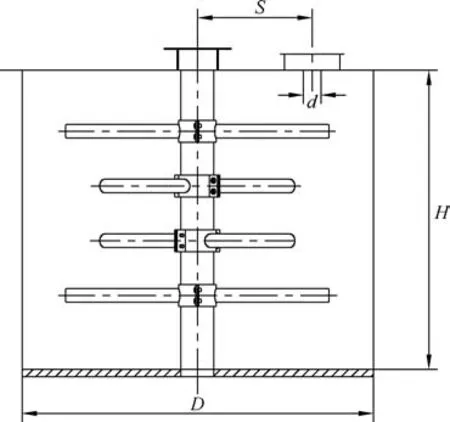
图2 熔融室几何模型Fig.2 Geometry model of the melting chamber

表1 熔融室几何参数Tab.1 Geometric parameters of melting chamber
塑料静置于熔融室底部,吸收热量,为保证塑料在熔融室中得以充分吸收热量,故而对熔融室进行优化设计,改善熔融条件,加快熔融,模型中搅拌轴对塑料起搅拌作用,为简化分析,不考虑搅拌轴的影响,先做初步研究分析,后续再进行系统分析。因此对模型进行简化,模型中只保留进风口、熔融室和筛网并使用Fluent中的Design Modeler进行几何建模,如图3所示,筛网如图4所示,筛网几何参数见表2。
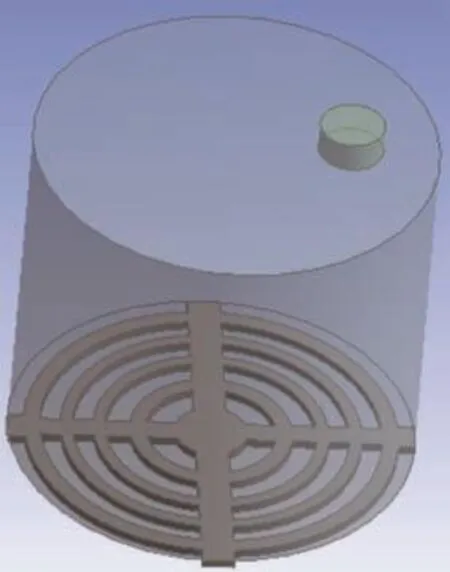
图3 熔融室Fig. 3 Melting chamber
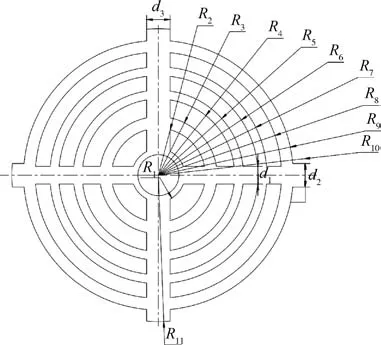
图4 筛网Fig.4 Sieve

表2 筛网几何参数 mmTab.2 Screen geometric parameters mm
2 网格的划分及边界条件的设定
设置进风管道上表面为入口,筛网间间隙为出口,进风管道与熔融室外表面为固体壁面。入口边界条件:入口采用速度入口;出口边界条件:出口采用压力出口,压力设置为0;固壁采用无滑移壁面条件;求解器设定为基于压力的求解器。入口边界温度为135℃,入口空气密度为1.225 kg/m3,比热为1 006.43 J/(kg•K),热导率为0.024 2 W/m•K,黏度为1.789 4×10-5kg/m•s。
3 数值模型的选择
由于本模拟涉及对流传热流动,需要求解标准的k⁃ε湍流模型和能量方程。
标准k⁃ε湍流模型的方程中湍流动能方程k和湍流耗散率ε如式(1)和式(2)[8]所示:
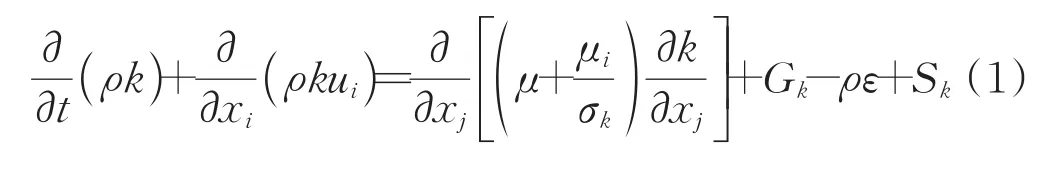
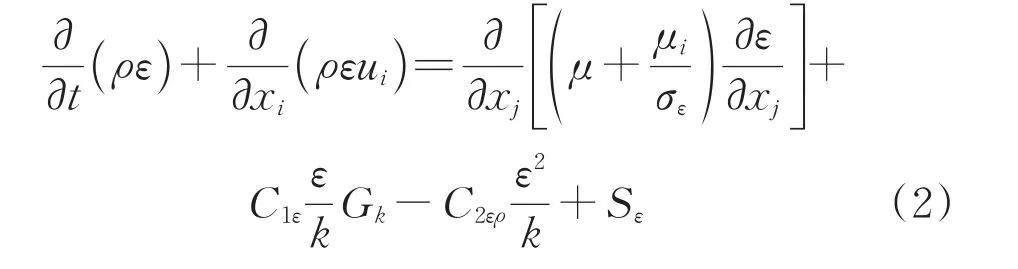
式中ρ——空气密度,kg/m3
k——空气紊流动能,J
t——时间,s
xi、xj——坐标位置
ui、uj——xi、xj坐标方向上的空气流速,m/s
μi——动力黏度,kg/(m∙s)
ε——紊流动能耗散率,%
Gk——由平均流速梯度产生的湍流动能,kg/(m∙s2)
σk——k方程的湍流普朗特数
σε——ε方程的湍流普朗特数
C1ε——经验常数
C2ε——经验常数
Sk——自定义源项
Sε——自定义源项
能量方程如式(3)[9]所示:
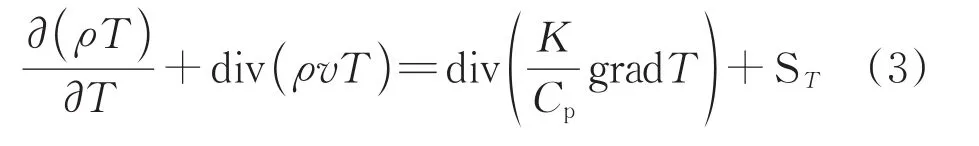
式中T——热力学温度
v——平均速度
K——流体传热系数
Cp——比热容
ST——黏性耗散项
4 Fluent模拟结果及分析
4.1 进风口直径对熔融室温度分布的影响
熔融室仿真参数设置如表3所示,为查看模拟结果建立中间平面,并为方便观察熔融室温度分布,将该平面简化为a、b、c、d 4条直线,取每条直线上相同若干点的温度数据,采用origin进行数据处理,代替该平面温度分布。塑料熔融时,大多处于熔融室中下部分,故在熔融室模型中下部分等距取4条直线,由进风口至筛网分别是a、b、c、d 4条直线。如图5所示,模拟结果如图6所示。

图5 熔融室直线分布Fig.5 Linear distribution of melting chamber
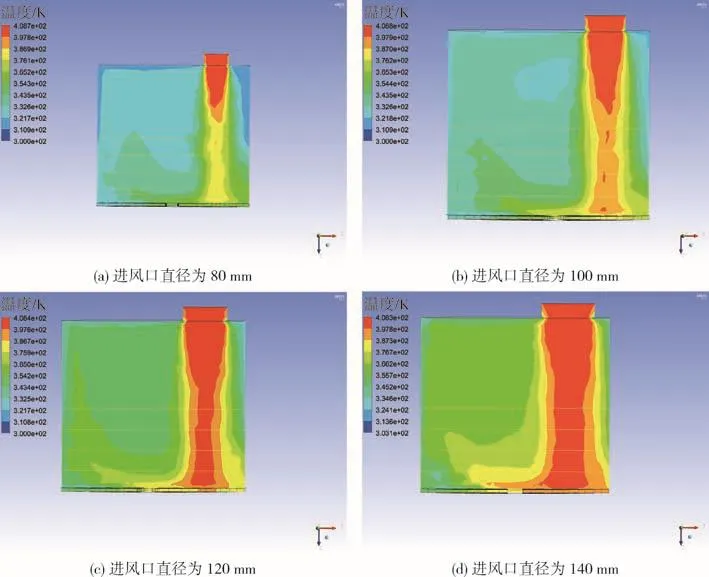
图6 不同进风口直径温度云图Fig.6 Model temperature clouds with different inlet diameters
表3 熔融室模拟参数Tab.3 Melt chamber simulation parameters
由图中分析得:随着进风口直径不断增大,沿进风口区域附近的温度明显增高,待该区域附近温度达到最高温度即边界温度,保持不变。采用origin进行数据处理,可得如图7所示结果。
结合熔融室模型分析点线图7可得:热风由进风口进入,温度最高,进入熔融室后沿进风口方向向周围流动,温度降低至稳定,最后到达熔融室壁面,温度最低。因此熔融室温度分布为:进风口最高,沿进风口左右迅速降低至平稳,最后流动至壁面,温度达到最低,逐级产生温差。最后比较1,2,3,4模型上相同直线温度数据,进行温度比较可得如图8所示结果。
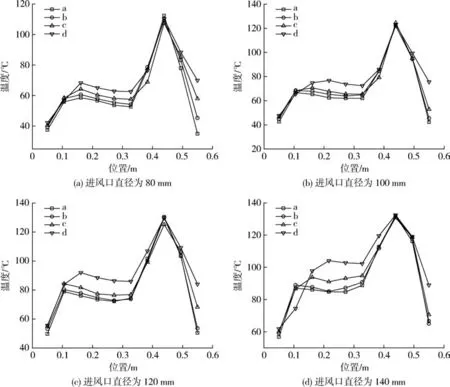
图7 不同进风口温度分布Fig.7 Different inlet temperature distribution
结合熔融室模型分析点线图8可得:温度最高点仍为进风口位,随着进风口直径地增加而不断增加,待进风口直径达到120 mm,温度达到最大并保持不变,即达到入口边界温度。但各图各直线左部分温度数据也随着进风口半径的增加而逐渐提高且直线趋于平缓,熔融室温差逐渐减小。可得结论:随着不断扩大进风口直径,熔融室温差减小,故为改进熔融室温度分布均匀性,应尽可能扩大进风口直径。
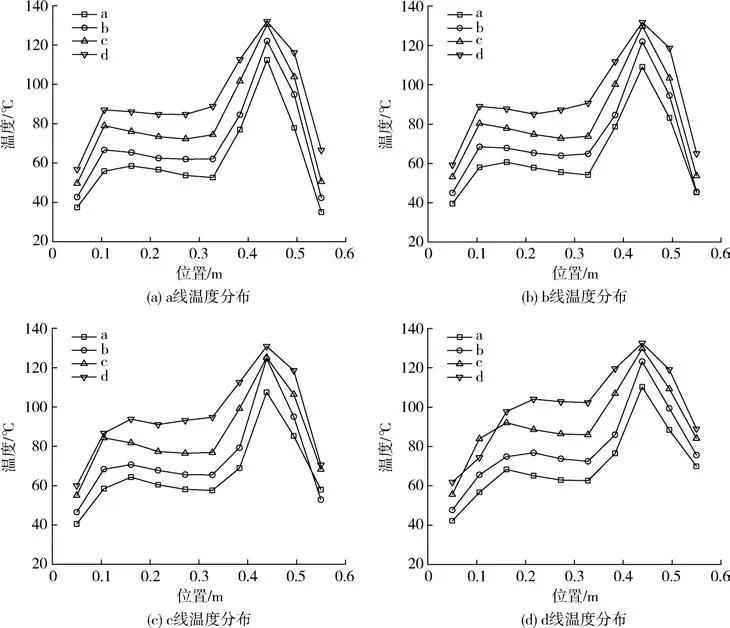
图8 各线温度分布Fig.8 Temperature distribution of each line
4.2 进风口位置对熔融室温度分布的影响
熔融室仿真参数如表4所示,模拟结果如图9所示。
表4 熔融室模拟参数Tab.4 Simulation parameters of melt chamber
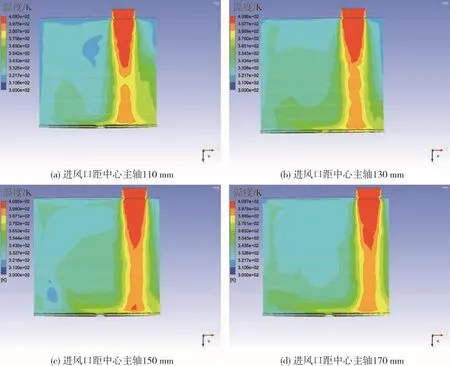
图9 对距中心主轴不同距离的温度云图Fig.9 Model temperature nephograms at different distances from the central spindle
由图中分析得:随着进风口远离中心主轴,温度最高点随进风口位置改变而变化,熔融室温度分布也发生相应的变化。采用origin进行数据处理,可得如图10所示结果。
结合熔融室模型分析点线图10可得:进风口仍是熔融室温度最高位,温度沿着进风口向两边降低至平稳。随着进风口远离中心主轴,温度最高处随着改变,熔融室其余位置温度分布也发生改变。各熔融室模型温度分布中,最高温度数值变化不大,但其余位置温度分布变化明显。第8模型中,熔融室左部分产生过大温差,即第4直线温度分布于其他3条直线温度分布差异过大,使熔融室温度分布不均匀;第5模型中,熔融室左部分虽没有明显的温差现象,但整体温度过低,均处于50~70℃范围内,与进风口温度分布差异太大,致使熔融室整体产生过大温差,整体温度分布不均匀,在模型6与7中,6的温度分布更加均匀,且与主轴差距不大。因此得:距主轴130 mm进风口的熔融室温度分布更加均匀。
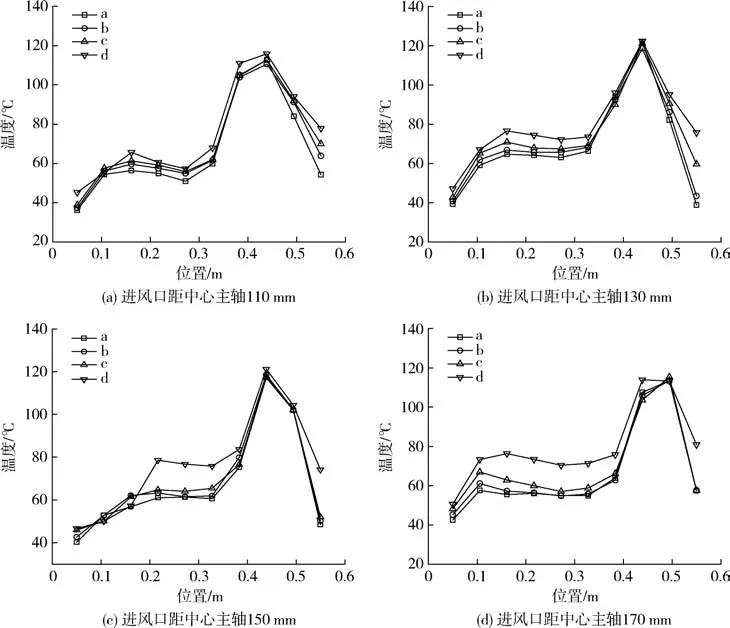
图10 不同进风口位置的温度分布Fig.10 Temperature distribution at different inlet locations
4.3 风速对熔融室温度分布的影响
熔融室仿真参数如表5所示,模拟结果如图11所示。
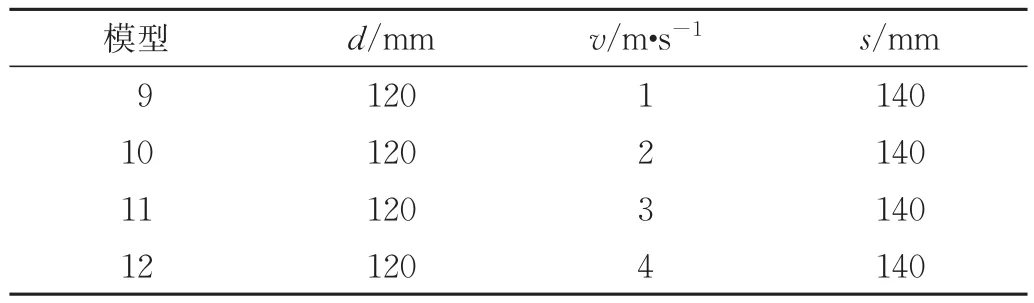
表5 熔融室模拟参数Tab.5 Simulation parameters of melt chamber
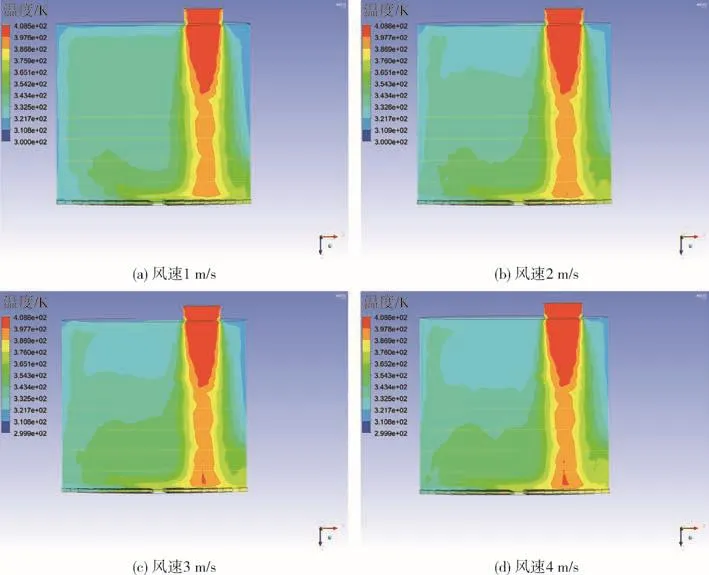
图11 不同风速模型的温度云图Fig.11 Temperature cloud diagram of different wind speed models
由图中分析得:随着风速的增加,熔融室温度分布并无明显变化。为仔细观察熔融室温度分布,采用origin进行数据处理,可得如图12所示结果。
结合熔融室模型分析点线图12可得:各熔融室模型温度分布中,最高温度数值变化不大,其余位置温度分布变化较为明显。模型9中,熔融室左部分第4直线均与其他3条直线温度差异过大,温度分布不均匀。模型10、11与12,随着风速不断增大,熔融室温度分布越趋于稳定,且随着风速不断地增大,熔融室左区域温度不断增加,即远离进风口位,但最高温度位及数值并没有明显改变。因此得:熔融室风速达到3 m/s及以上,熔融室温度分布均匀且稳定。
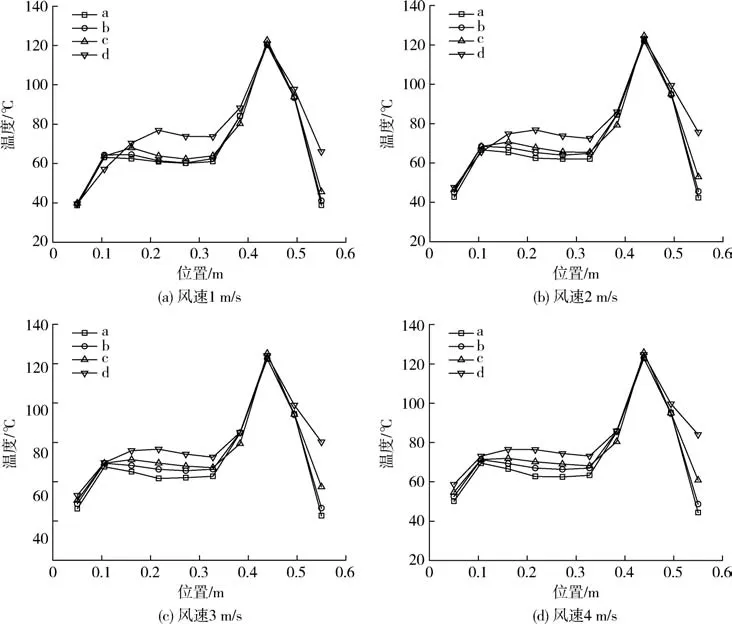
图12 不同风速模型的温度分布Fig.12 Temperature distribution of different wind speed models
5 多参数正交模拟设计
上述模拟主要是对熔融室各参数的单参数影响规律分析,多参数的优化更能直观地展现各参数对熔融室温度均匀性影响的规律。正交法是一种广泛使用的多参数结构优化方法,使用正交试验法后,可以分析计算各因素对模拟结果的影响,并通过图表形式表现出来,再通过方差分析综合比较,最后确定优化参数[10]。影响熔融室温度均匀性的3个参数为进风口直径d、进风口距中心距离s和进风口风速v,选取3个水平。根据因素及水平划分,采用3因素3水平的正交模拟矩阵,采用正交表L9(33),如表6所示。考核指标为高温区与低温区温度的差值,即为进风口区域温度与远离进风口熔融室区域温度的差值,得到相应的正交表。
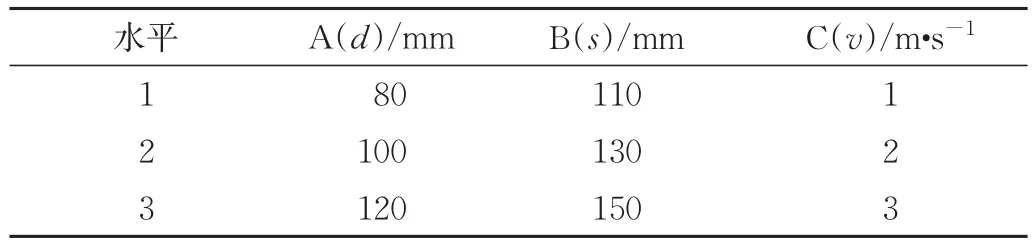
表6 影响熔融室温度分布的因素和水平Tab.6 Factors and levels that affect the temperature distribution of the melting chamber
考察3因素3水平的差值影响,所有不同的模拟条件共有33个,根据正交试验设计,安排9组仿真模拟,模拟的目的是得到温度差值影响最小的参数及各个参数对温度差值影响优先级,最后得出最佳参数组合。
通过表7观察正交模拟结果,进行方差分析得表8。通过正交试验和方差分析,各参数对试验指标的影响可由方差分析的显著性得到,即:进风口直径=进风口距中心距离>风速。
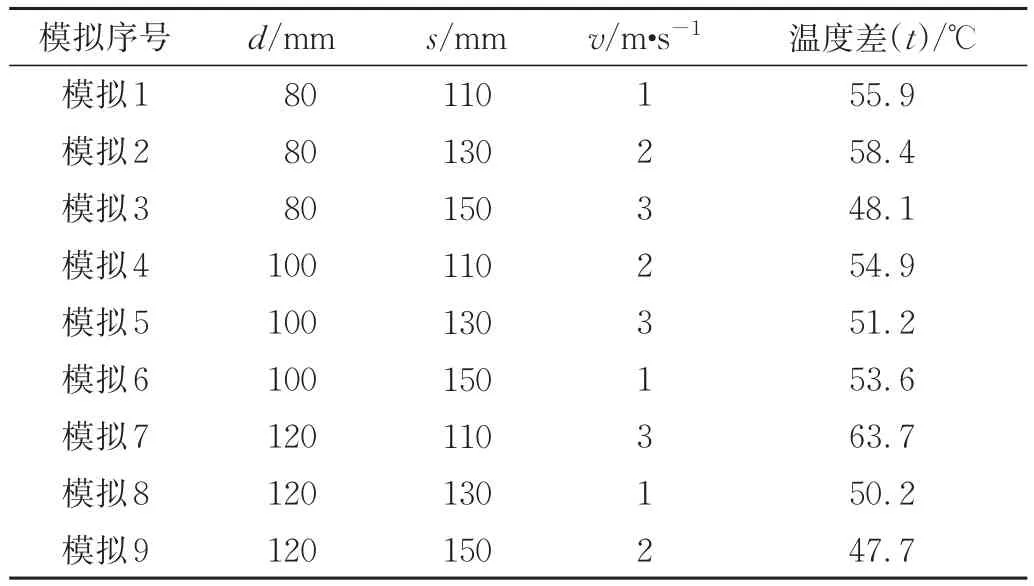
表7 熔融室参数正交模拟表Tab.7 Orthogonal simulation table of L9(33)melting chamber parameters
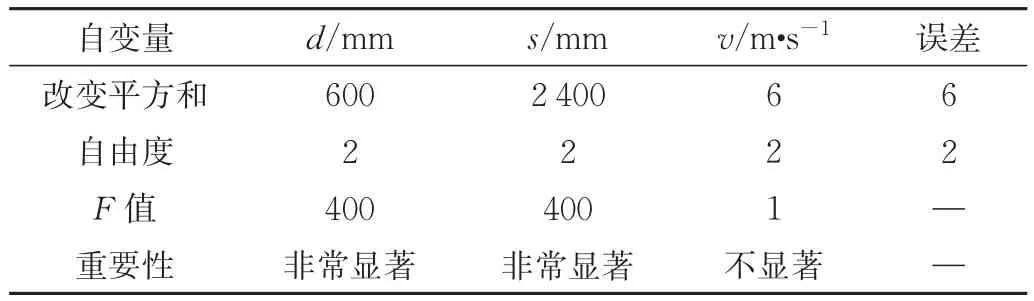
表8 方差分析表Tab.8 Analysis of variance table
根据正交模拟的优化结果,模拟中的最优结果应为A3B3C2,即进风口直径为120 mm,进风口距中心为150 mm,进风口风速为2 m/s。熔融室温度差为47.7℃;
6 结论
(1)当其他条件不变时,熔融箱体内温度分布随着进风口直径的增大而显著增加;随进风口距中心主轴发生相应变化;随进风口速度增大而无明显变化;
(2)各参数对温度均匀性的影响:进风口直径=进风口距中心距离>风速,且为使熔融室箱体内温度分布合理且均匀,废旧塑料得以充分地吸收热量,因此采用进风口直径为120 mm,进风口距中心为150 mm的优化方案。

