行人导航状态识别与传感器优化选择

杨秀莲，李 娟，王梦杰，吕 杨，孙秀慧，戴洪德

(1.鲁东大学 数学与统计科学学院统计系，山东 烟台 264025；2.海军航空大学 航空基础学院，山东 烟台 264001)

0 引言

惯性传感器是实现高精度行人导航的重要技术[1]。随着科学技术的发展，我国行人导航的研究取得了飞速的发展，基于微机电系统(MEMS,micro-electro-mechanical system)惯性传感器的行人定位由于其极强的环境适应性和抗干扰性而得到了广泛的研究[2-3]。惯性导航系统可由MEMS陀螺仪、加速度计和磁强计等多种惯性传感器组合构建。惯性导航系统具备了体积小、质量轻、成本低、部署方便、可靠性高和易于集成的特点，使得惯性系统可以独立实现人体的定位导航，可用于复杂的室内外环境使用，能为人们提供更多工作生活的便利。因此，针对MEMS惯性传感器的导航技术研究对我国行人导航的发展具有重要的意义。

应用在行人导航的MEMS惯性传感器可分为单轴惯性传感器、双轴惯性传感器和三轴惯性传感器3种组装系统。目前，研究行人运动状态研究领域中所采取的惯性导航系统不尽相同，Rebeiz和Judy在研究人体运动状态采取了用三维加速度传感器作为采集人体运动信息的有效设备器件[4-5]。Padgaonkar在研究人体运动状态时分别采用了包括一维加速度计、二维加速度计和三维加速度计组合的传感器系统[6]。Giansanti针对六维或九维加速度计的行人导航组合测试系统进行了深入探究[7]。Prasa在研究人体运动状态尝试采取十二维加速度计进行分析[8]。Rehbinder和Hu在研究人体运动状态时采取了基于MEMS加速度计和MEMS陀螺仪组装的二维传感器，但最终实验结果存在角度漂移问题[9]。随着惯性人体运动研究得到广泛的关注，结合科技技术的日益发展，Morris等研究者提出了在三维空间中研究人体运动状态[10]。Bachmann在研究人体运动状态采取了九维惯性导航系统[11]。

通过查阅国内外相关文献可发现，有大量研究者均基于高维组合传感器研究行人惯性导航系统，但传感器数量的组合安装大多依赖研究者的主观经验，当采用传感器的数目大于实际最优检测效果数目时，优化传感的方法选择的传感器会表现出明显的优异性，以此可避免过多传感器配置将引入的冗余信息。本文将集成了三轴陀螺仪、三轴加速度计的MEMS惯性传感器作为导航元件，基于Foxlin[12]系统阐述的脚绑惯性传感器的行人步态区间测试思想，研究X、Y、Z各轴向加速度及角速度组合的行人步态状态识别，最终根据行人运动状态的识别效果实现惯性传感器配置优化，给出最优组合的惯性传感器配置。

1 惯性行人导航实验系统设计

1.1 实验系统结构

惯性行人导航系统由电源、惯性传感器、导航计算机和显控设备构成[13]。电源用于向整个系统供电，惯性传感器用于获取并输入行人运动的运动数据，导航计算机是对传感器输入的数据进行解算并将导航结果输出到显控设备，显控设备用于输出导航结果以及输入指令控制导航计算机。系统硬件结构如图1所示。

图1 惯性行人导航系统硬件结构

基于系统的硬件结构图，利用计算机代替导航计算机和显控设备，并利用计算机的电源为惯性传感器供电，实现了一个将MEMS传感器安装于脚跟部位的惯性行人导航系统[14]，实验系统实物如图2所示。

图2 惯性行人导航系统实物模型

1.2 MEMS惯性传感器

本文利用荷兰Xsens公司生产的Mti-G-710系列MEMS惯性传感器作为导航元件。在行人导航状态检测实验时，惯性传感器可分为3个轴方向，其中行人前进方向为X轴，左侧方向为Y轴，朝上方向为Z轴。其实物图和内部结构如图3所示。

图3 Mti-G-710系列MEMS惯性传感器

Mti-G-710系列MEMS惯性传感器尺寸小、重量轻，可以通过RS232接口将三轴角速度、加速度以及磁场强度信息实时输出，其物理指标如表1所示。

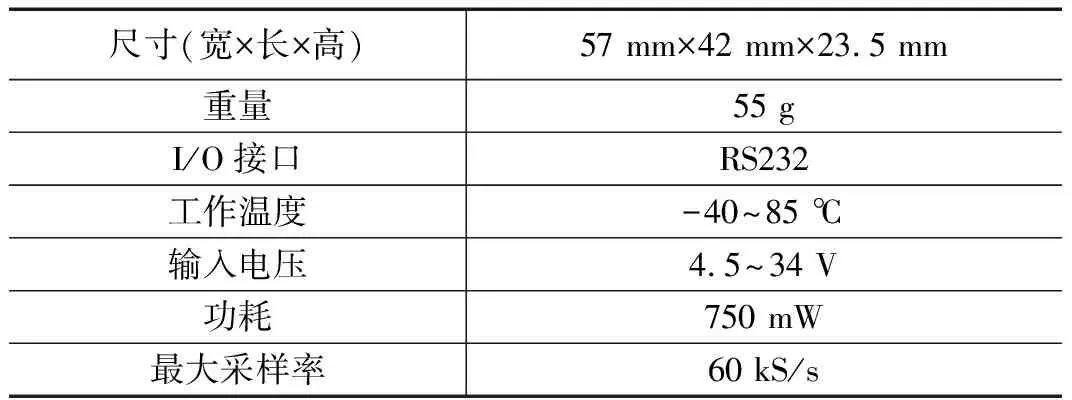
表1 MEMS惯性传感器物理指标

Mti-G-710系列MEMS惯性传感器中陀螺仪、加速度计和磁强计的性能指标如表2所示。

表2 MEMS惯性传感器性能指标

2 行人导航脚部运动状态实验分析

2.1 行人行走状态脚部运动分析

根据人体运动学可将行人行走过程中足部的变化用步态来进行描述[15]，根据行人步行过程存在周期性的步态更迭特点，因此可将每个运动周期分为两个区间，一个是全脚掌着地时的零速区间，另外一个是包括抬脚跟、空中摆动和脚跟着地3个部分的非零速区间。因为足部运动具有静止-运动-静止交替变化特点，所以安装在脚跟部位的惯性传感器MIMU输出的行人脚部运动数据会呈现出与行走频率一致的周期性变化规律，可大体将行人的一个步行周期分为抬脚跟、空中摆动、脚跟着地和全脚掌着地4个过程。课题组前期研究中，分析得到行人行走时步态更迭状态如图4所示[16]。

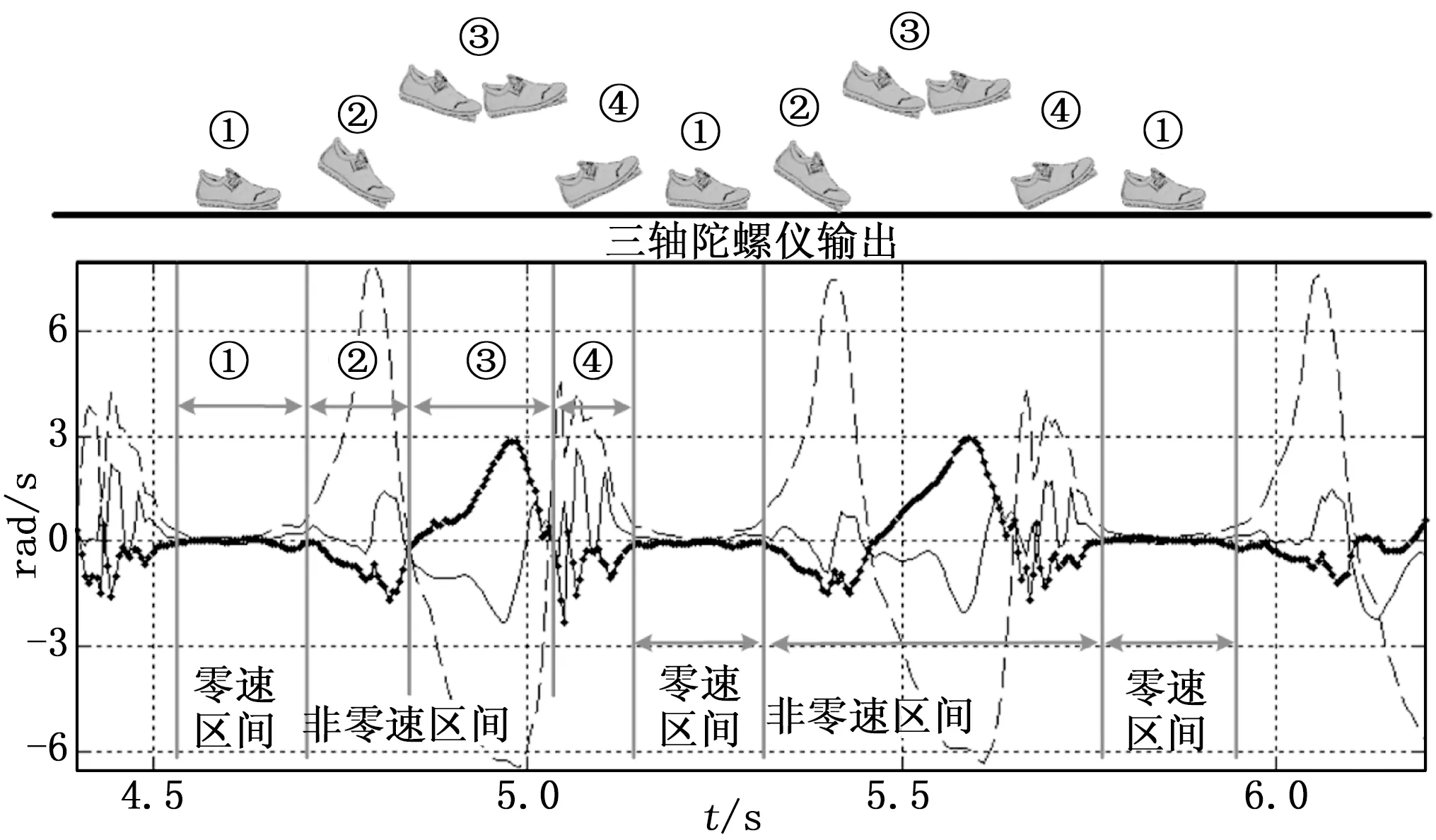
图4 行人行走步态分析

2.2 基于惯性传感器输出的行人步态分析

根据惯性行人导航实验系统获取行人行走过程中惯性传感器输出的脚步惯性步态数据，可寻找行人步态与惯性传感器输出值的对应关系。分别探究行人纵向、前向、垂向的加速度和角速度速度变化，可检测出行人步态的零速区间。实验设计行人在水平路面上沿直线行走过程中，惯性传感器中加速度计和陀螺仪计输出的9个步态周期的运动规律如图5和图6所示。

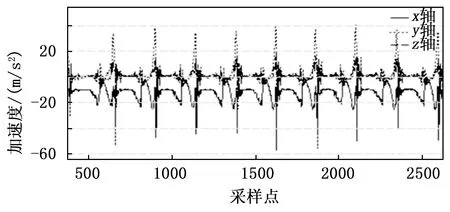
图5 行人行走过程中加速度计输出值

图6 行人行走过程中陀螺仪计输出值

从图5和图6可明显看出，行人行走过程中三轴加速度计和三轴陀螺仪计输出值均呈现出明显的周期性变化规律，每个周期内加速度与角速度的幅值变化规律可大体包括：幅值波动相对稳定区间和幅值波动较大区间。该变化规律与图4分析的行人行走的步态周期有着明显的关联性。图5和图6中加速度和角速度幅值变化稳定段即为行人步态的零速区间，该区间由于行人脚部步态处于全脚掌着地的静止状态，所以惯性传感器输出的加速度和角速度趋向平稳；加速度和角速度幅值变化较大阶段即为行人步态的非零速区间，该区间由于行人脚部步态处于抬脚跟、空中摆动的运动状态，所以惯性传感器输出的加速度和角速度呈现不稳定的幅值波动。

2.3 多种聚类模型的行人运动状态识别分析

聚类分析指将无标签的数据集划分为不同簇的过程，是一种无监督的分类方法[17]。聚类算法在统计学、数据挖掘、模式类别等研究领域广泛使用，是一种非常重要的数据分类研究工具[18]。聚类的标准是使簇内样本相似度尽可能大、簇间样本相似度尽可能小。因此，对高维惯性行人导航的空间数据对象划分可通过聚类目标函数的优化问题来解决。

许多研究人员运用各种聚类对导航系统的优化做出了贡献，陈淼证明了在一个复杂的室内环境，自组织映射算法可以将高维变量映射到一个一维或二维的平面上，从而提高系统的实时定位性[19]。传统的室内定位方法采用标准高斯模型对参考点上接收的信号强度进行建模[20]。胡叶证明了K均值聚类可以有效识别运动状态[21]。

本文拟采取K均值聚类(K-means)、自组织映射(SOM)、混合高斯聚类算法(EM-GMM)3种较为经典聚类算法识别行人的运动状态。综合对比各聚类算法分类效果，最终实现最优行人运动状态检测。

1)K-Means算法：

K-Means算法是最经典的聚类算法之一，处理高维数据集有较高的效率且具有可伸缩性[22]，是一种非常重要的数据划分研究算法。对于给定的原始三轴加速度和角速度数据集，每个样本包含P个变量，记Xik表示数据集中第k个变量第i次观测值,i=1,2,…,n，k=1,2,…,p。基于K-Means算法进行行人步态零速识别的具体算法步骤为：

(1)预先在数据集中随机选取k个初始聚类中心,计算其余数据对象与聚类中心的欧氏距离。基于X、Y、Z轴加速度和角速度六维变量，则样本点的欧式距离公式如下：

(1)

其中:D表示样本间的距离，xi和xj为样本点,表示三维空间X、Y、Z轴的加速度或者角速度数据点;k为样本特征的维数；xik与xjk表示样本中不同变量。

(2)找出离目标数据对象最近的聚类中心,并将数据对象划分到聚类中心所对应的簇中。一般情况下，聚类类别数是未知的，此处假定数据集包含k个类别C1,C2,...,Ck,迭代次数为m，则K-means聚类算法的聚类准则函数选择误差平方和准则函数的计算公式如下：

(2)

其中:p表示类Ci中所有样本个体，Mi表示类Ci中所有样本的算数平均值。Jm表示数据样本被聚类成k个簇时的误差平方和，即聚类结果误差的大小。当误差平方和不再变化或目标函数收敛时，样本与聚类类别中心之间的距离的平方之和可达到最小。

(3)计算各簇中数据的平均值设定为新的聚类中心,然进行下一次迭代,直到聚类中心不再变化或达到最大的迭代次数停止。

2)SOM算法：

自组织特征映射(SOM，self-organizing feature map)[23]是由芬兰学者Kohonen于1981年提出的一种特殊的神经网络模型。SOM对行人步态的零速检测分类训练步骤如下：

(1)首先给SOM网络个训练参数赋予小的随机数初始值。

(2)从三轴加速度和三轴角速度数据集中选取输入样本Xi={x1,x2,…xn}。

(3)计算权向量与输入样本间的欧式距离，其欧式距离公式如下：

(3)

(4)选择最小距离的样本点作为最合适的神经元i(x)=minDij。

(5)调整输出层领域Ng(t)内的各个神经元与输入层神经元之间的链接权，其公式如下：

wij(t+1)=wij(t)+η(t)×(xj-wij(t))

(4)

(5)

wij(t+1)=wij(t),j∉Ng(t)

(6)

式中，T为总学习次数；wij(t+1)表示t+1时刻输入神经元i与输出神经元j之间的连接权；Ng(t)表示t时刻以获取神经元g为中心的领域范围。

(6)更新学习率和领域。更新函数如下所示：

(7)

(8)

(7)依次输出加速度和角速度训练样本。当数据集再次选取一个未训练的样本时，将其传送给输入层，然转到步骤(3)，直到全部样本训练结束。

(8)增加学习步。此时令t=t+1，再转到步骤(2)，直至步长t=T时停止。

3)EM-GMM算法:

将原始整个三轴加速度和角速度样本数据记为Y={X,Z}。其中X={x1,x2,…,xn}为加速度或角速度观测数据，Z={z1,z2,…,zn}为隐含变量。则原始数据对数似然函数中的极大参数值为：

(9)

求其似然函数的概率：

(10)

选取高斯混合模型参数的初始值，求解最大后验概率估计：

(11)

根据选取的模型参数初始值，解出高斯混合模型对数似然函数的期望值：

EQ[logp(θ|Y,Q)|θ(i),Y] =

(12)

式中，Q表示不可观测的隐含数据，θ(i)表示第i+1次迭代后验标准差。

通过迭代，最终得到样本的参数估计值为：

(13)

(14)

(15)

行人步行状态按速度快慢可划分为慢速、常速、快速、慢跑、跑步5种运动状态。基于惯性传感器输出的行人步态数据作为初始样本，将原始数据集进行归一化数据预处理，分别基于K-means、SOM、EM-GMM聚类算法进行行人5种运动状态识别分析。

从无监督学习聚类原理综合评估指标出发，依赖于聚类评价中的内部度量指标，针对本文建立的3个无监督聚类模型，最终选取轮廓系数(SI)[24]、戴维森堡丁指数(DBI)[25]、卡林斯基-哈拉巴斯指数(CHI)[26]3个指标及算法运行时间进行综合对比，确定最优化模型的聚类算法。具体详细数据如表3所示。

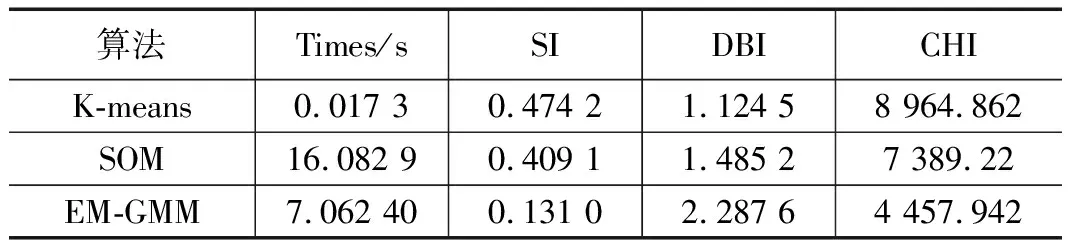
表3 3种聚类算法评估对比表

从表3可知，根据对比分析的各聚类模型中K-means执行时间最快；将其他3个评估指标进行定量分析可得出，针对平均轮廓系数对比，其中K-means聚类SI值最大，即K-means聚类模型的运动状态识别效果最佳。针对戴维森堡丁指数对比，也可看出K-means聚类模型的DBI值最小，其意味着类内距离越小，同时类间距离越大，表明聚类效果越佳。针对卡林斯基-哈拉巴斯指数对比，K-means聚类模型远大于其他聚类模型的CHI值，表明聚类效果优于其他模型。基于以上4个指标分析，综合聚类精准度和高效性，可得出K-means聚类模型为最优行人导航状态识别模型。

为了进一步直观展示K-means的聚类效果，利用主成分分析法将原始六维数据降维到二维可视空间中，第一主成分记为Dim1，第二主成分记为Dim2。行人在行走过程中5种不同运动状态聚类效果如图7所示。

图7 K-means聚类行人运动状态识别效果图

由图7可知，第一、第二主成分的最大特征值占6个特征值之和的比例分别为36.6%和32.1%，即二者包含了原数据约70%的信息，当k=5时簇与簇之间分隔较为明显。

3 基于K-means模型的传感器优化分析

3.1 二维、三维传感器运动状态识别

本章将分析基于K-means聚类优化方法进行精简传感器，进一步讨论对传感器精简优化后模型的有效性，实现传感器的优化配置的设置参数，为有效获得行人导航状态识别研究提供参考。基于K-means聚类算法对二维、三维的行人导航惯性传感器配置输出的数据集进行自动分类，探讨分类识别行人步行过程中的5种运动状态，即慢速、常速、快速、慢跑、跑步。二维传感器组合聚类图见图8，三维传感器组合聚类如图9所示。

图8 二维行人惯性导航系统不同组合K-means聚类图

图9 三维行人惯性导航系统不同组合K-means聚类图

图8(a)～(c)的聚类均存在大量离散点；图8(d)～(f)的聚类各簇均较集中，离散点较少，可初步鉴定二轴向角速度聚类效果较二轴向加速度的聚类效果好。

在三维惯性传感系统不同轴向的聚类效果中，图9(b)的聚类各簇较集中，图9(a)的聚类存在大量离散点，说明X、Y、Z三轴角速度组合的五簇聚类聚集效果较三维X、Y、Z三轴加速度组合的五簇聚类效果理想。

3.2 对比研究

为对比二维、三维与原始六维的行人运动状态识别效果，计算聚类综合评估指标SI如表4所示。

将表4的结果表现为折线图，如图10所示。

表4 聚类综合评估SI指标

图10 二维、三维、六维综合评估SI指标比较

从聚类综合评估SI指标图10比较可以看出，二维X、Z轴向角速度和Y、Z轴向角速度的空间组合在识别行人不同运动状态聚类效果最好，其SI值分别达到0.58和0.59；其次识别行人不同运动状态效果较为理想的为二维Z轴向的加速度和角速度和三维X、Y、Z轴向角速度组合，各簇被完全的分离为5种类别，簇聚类集中，且其SI值也分别达到0.56、0.51。反观六维空间中三轴加速度和角速度组合的SI值未达到0.5，其行人运动状态识别聚类效果较不理想。综合以上实验分析表明，在不同维传感器识别行人不同运动状态中，二维、三维、六维SI指标差别不大，综合考虑六维可能出现的维数灾难问题，得出二维和三维行人惯性导航系统即可有效实现行人运动状态识别。

4 实验结论与分析

实验结果显示，在K-means聚类、EM-GMM聚类和SOM聚类算法中，K-means的执行时间最快，SI值最大，DBI值最小，CHI值也远大于其他两种聚类，因此基于K-means聚类算法对行人运动状态识别过程进行传感器优化。

基于K-means聚类模型探究了不同组合传感器配置测试效果。实验结果显示，二维Y、Z轴向角速度和三维X、Y、Z轴向角速度的空间组合在识别行人不同运动状态聚类

效果时，其SI值分别达到0.59和0.51；而六维空间中三轴加速度和角速度组合的SI值未达到0.5。可见，优化后的二维和三维行人惯性导航系统即有效实现行人运动状态识别。

5 结束语

为实现较少传感器即可完成行人导航状态识别的目标，设计惯性行人导航实验系统，针对二维、三维、六维行人导航惯性传感器数据进行传感器优化研究，提出了传感器优化选择方案。

结论表明，基于二维、三维惯性行人导航传感器信息即可实现行人状态识别，充分体现了传感器优化选择方案的经济性、便捷性、高效性。