基于行人安全的交通信号灯智能控制算法研究

张乾隆,胡智群,肖海林

(湖北大学 计算机与信息工程学院，武汉 430062)

0 引言

随着城市规模的不断扩大，城市交通拥堵问题愈加严重。为了解决拥堵问题，如何提高车辆通行效率近几年来被广泛地进行研究。然而，除了驾驶车辆，行人也是使用道路的主要元素。追求车辆通行效率所带来的潜在行人安全问题也不容忽视。据交通事故统计[1]22%的行人死亡事故发生在有标志的人行横道上，超过30%的行人死亡可以归因于非法穿越行为。因此，综合考虑车辆效率和行人安全的交通信号控制机制变得至关重要。

传统的基于效率的交通信号控制通常是基于历史车流量预设的固定配时方案，或者基于当前车流状态调整交通信号时长，或者基于人工智能算法智能调整信号配时方案。例如SCOOT[2]和SCATS[3]系统已在全世界广泛使用。但是这些信号控制方案缺乏自适应性和预见性，甚至导致大量的人力负担。近年来，人工智能技术在交通控制领域的应用有效地解决SCOOT，SCATS系统所面临的问题。文献[4-5]提出利用Q学习算法将交通信号控制问题转换为马尔可夫决策问题，通过与交通环境的不断交互反馈，无需复杂的数学模型，不断积累经验学习最佳的控制策略。由于Q学习需要通过表来存储所学习到的Q值，当网络状态复杂且高维时，需要占用较大的内存资源，无法适应于复杂的场景。文献[6-7]对Q学习进行改进，将DQN算法应用在交通信号控制，通过深度神经网络对Q值进行近似，选取最佳交通信号灯动作。由于DQN算法依赖于找到最大近似Q值，当处理连续动作的交通场合时，需要对每个步骤迭代优化，随着迭代的增加，量化误差越来越大，无法在连续复杂的交通网络中找到最优策略。文献[7]提出利用DDPG算法解决Q学习应用在交通场合时动作空间不连续问题，利用策略网络和目标网络组成的双网络结构，在与交通环境交互探索时对所选Q值动作不断进行梯度计算调整，使得智能体倾向于生成车辆效率更好的动作选择，不断引导智能体找到最优策略。这些策略方法根据路口车流量自适应的调整配时方案，能够有效地提高路口的通行效率，缓解交通拥堵问题。但是这些方案只注重驾驶车辆，没有考虑行人因素。由于车辆和行人速度相差较大，只考虑车辆拥堵现象，会导致绿灯期间行人不能完全通过马路，与车辆产生冲突，安全受到威胁。据文献[8]研究发现79%的行人在交通灯变红之前没有通过交叉路口。

在有关行人安全过马路的研究中，文献[9]提出一种行人手动激活控制方案，在有过马路需求时，行人通过手动按下激活按钮改变交通信号灯状态，以保障安全通过路口。但是经过研究发现[10]，这种将行人与车辆分离的控制方案，实际上大大影响了交通信号灯控制系统的整体效率。Guo等人[11]和Midenet等人[12]的研究发现车辆和行人信号协调控制对交叉口安全具有积极影响。

为了进一步探讨车辆与行人行为对交通信号控制的影响，通过仿真、数学模型等手段研究协调控制被广泛研究。文献[13]考虑行人因素的条件下，提出一种基于遗传算法的交通信号灯控制方案。通过适应度函数表示车辆与行人的等待数量，评价候选染色体的有效性来调控信号灯。然而所考虑的仅仅是减少行人或者车辆的等待队列长度，没有考虑车辆和行人整体协调，在遇到两者不公平的情形下，设定车辆优先级大于行人。文献[14]综合考虑了车辆和行人的队列长度，提出一种基于分布式多智能体强化学习的交通信号控制方案，实现车辆与行人等待时间最小化。但是忽略了行人在绿灯期间可能无法完全通过路口，造成与车辆冲突的问题。文献[15]提出了一种考虑车辆总延迟和行人安全的全网络交通信号策略。通过建立行人-车辆混合流网络宏观模型智能调控交通信号灯，过程中考虑到绿灯闪烁期间行人违规率较高，在每个绿灯闪烁期间结束时引入一个动态全红阶段，并根据违规行人的数量自适应调整其持续时间。但是动作空间里固定了绿灯闪烁时间而且持续时间较长，由于行人往往忽略绿灯闪烁剩余时间强行通过路口，会导致每一动态全红阶段持续时间都较长，大大影响了车辆通行效率。

为了协调车辆效率和行人安全，本文提出了一种基于行人安全的交通信号灯智能控制方案，通过对交叉口流量的实时观测，综合考虑行人违规和车辆效率存在的矛盾，精准设计强化学习架构中的奖励函数引导智能体学习，智能地调控交通信号周期时长，相位顺序以及相位持续时间，实现交叉路口安全高效的智能控制，同时，采用基于优先经验的样本采样和方差缩放，加速了算法收敛。研究结果表明，基于行人安全配时方案在行人与车辆冲突量，车辆的排队长度、等待时间和平均速度等方面均优于固定配时方案和DQN配时方案。

1 系统模型和算法设计

1.1 DDPG算法

在交通信号灯控制中，自适应地调整周期时长、相位顺序和相位持续时间可以看成典型的马尔可夫决策问题，它很好的符合强化学习(RL,reinforcement learning)框架。智能体通过和交叉路口环境交互，获取环境状态st，随后采用“试错”机制寻找最佳策略π。在每次探索过程中，智能体根据所选策略执行动作at，动作执行后将积累的奖励值rt和交叉口下一状态st+1返还给智能体，智能体以奖励值为导向对动作评估，不断更新策略，如此循环以寻找最大预期值Q。如公式(1)：

Qπ(s,a) =E[rt+γrt + 1+γ2rt + 2+...|st=s,

(1)

式中,Q(s,a)定义为智能体接收到交叉路口车辆和行人状态s时，交通信号灯采取动作a时所获得的未来累计奖励；γ∈[0,1]为折扣因子，表明了未来交通信号灯配时方案回报相对于当前配时方案回报的重要程度。

随后通过贝尔曼公式不断更新值函数直至逼近最优值函数，由此智能体学习最优策略π*，如公式(2)：

(2)

DDPG算法是一种基于策略梯度的RL算法，可以通过与交通系统在线互动输出连续的动作。算法采用行动者-评判家(AC，actor-critic)框架，通过相同的神经网络架构，构成当前Actor网络和Critic网络，目标Actor网络和Critic网络，协作完成算法的决策与更新。

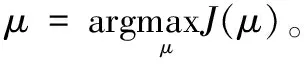
▽θμJ≈E[▽θμQ(s,μ(s|θμ)|θQ)=

E[▽aQ(s,μ(s)|θQ)▽θμμ(s|θμ)]

(3)

当前Critic网络用于拟合并参数化Q函数为Q(s,a|θQ)，并采用均方误差形式完成对当前交通信号灯配时方案的实时评估，具体形式如公式(4)：

(4)

式中,yi=ri+γQ′(si+1,μ′(si+1|θμ′)|θQ′)，μ′和Q′分别对应目标Actor网络和目标Critic网络。其中，目标Actor网络用于输出估计的交通信号灯配时方案，目标Critic网络用于输出对估计的交通信号灯配时方案评估。

当前Actor网络和Critic网络通过从记忆库中采样实现更新，而目标Actor网络和Critic网络的更新采用软更新的形式，能够使得目标网络参数变化小，训练更易于收敛。软更新的具体形式如式(5)：

θμ′←τθμ+(1-τ)θμ′

(5a)

θQ′←τθQ+(1-τ)θQ′

(5b)

1.2 DDPG算法改进

1.2.1 交叉口行人交通背景

行人在穿越路口时，往往不会注意绿灯剩余时间，经常会发生还没有完全通过路口，信号灯就变成了红灯的情况；老年人和儿童在通过路口的时候，往往会因为速度过慢而不能在绿灯期间通过路口；携带较多、较重物品的行人在通过路口时同样也会遇到相同的情况。这些情况下，行人安全难以保证。行人在规定绿灯时间内，不能按时通过交叉口，极易和车辆产生冲突，一方面行人安全难以保证，另一方面造成交通阻塞。以前的交通信号灯智能控制方案往往只专注于提高车辆效率，而忽略了行人，这实际上有很大的安全隐患。因此，智能交通有必要将行人不确定因素考虑进去，尤其是行人较多的例如学校、医院等旁边的交叉路口。

通过实际行人交通背景我们可以知道，行人经常会发生不能在规定时间内通过交叉口的情况[16-17]。因为强化学习特殊的“试错”学习机制，这实际上可以作为一条条宝贵的“学习经验”供智能体学习，以保证智能体能够有效的学习行人行为，进而保障行人安全。

1.2.2 PRE-DDPG算法设计

DDPG算法中当前Actor网络和Critic网络在采样更新时认为记忆库中所有经验都一样重要，因此它等概率地从经验池中选取一定数目的样本来训练网络。而实际上，通过行人交通背景分析知道，在交叉口行人不能按时通过时，智能体理应获取一个较差的“经验”，以避免这种情况的发生。因此，为了更有效地保证行人安全，合理处理交叉口行人与车辆行为实际经验，结合奖励值函数的精准设计，提出一种基于优先经验回放的DDPG(PER-DDPG，DDPG with prioritized experience replay)行人安全算法，并在记忆库满了后对方差进行0.999的缩放，以提高优先级大的样本的利用率，进而提高学习的效率，加快算法收敛。TD误差δ(t)计算如式(6)所示：

δ(t)=Rt+1+γQ(St+1，At+1)-Q(St,At)

(6)

定义抽取样本的概率如式(7)所示：

pi=|δ(t)|+ε

(7)

其中:ε用于防止概率为0。

为了避免每次抽样都需要针对p对所有样本排序，采用SumTree的树形结构对数据进行存储。SumTree是一种树形结构，每片树叶存储每个样本的优先级p，每个树枝节点只有两个分叉，节点的值是两个分叉的和。数据采样时，将优先级p的总和除以抽样数，得到区间数，然后在每个区间里随机选取一个数，将此数从SumTree的根节点开始按照一定规律向下搜索，最后将搜索得到的优先级p与样本数据相对应，即可实现更为高效的经验回放。SumTree结构如图1所示。

图1 SumTree结构图

1.3 基于行人安全智能交通灯控制模型

本小节主要阐述行人安全智能交通灯控制算法中状态、动作和奖励的设计和信号灯控制模型的建立。

1.3.1 状态

状态为在每一时间步中，智能体接收到关于交叉路口环境的定量描述。本设计将路口车辆等待数量，行人与车辆的冲突量作为状态输入。定义状态表达式如下所示：

st={w1,...,wn,v1,...,vn}

(8)

式中,w1,...,wn表示道路nn上车辆的平均等待数量；v1,...,vn表示人行横道n上行人与车辆的冲突量。

1.3.2 动作

本设计将动作设置为交通信号灯周期可变、相位可变和相位持续时间可变。定义动作如式(9)所示：

at={c,p1,...,p6,d1,...,dm}

(9)

式中,cc代表决定下一周期持续时间的时长，为避免周期过大或过小，将周期限制在内[cminT,cmaxT]，cmin，cmax，T分别取0.6，2，90；p1,...,p6表示下一周期相位持续顺序；d1,...,dm表示下一周期内各阶段的持续时长的比例因子，通过与环境交互后由softmax归一化处理确定。

1.3.3 奖励

为有效保证行人安全，我们设定只有在绿灯亮起范围内通过路口的行人才是合法的，其他各阶段行人出现在人行横道上均视为违规行为，视为与车辆正常行驶发生冲突，此时行人数量称为行人与车辆的冲突量。由此，在评价行人过路口是否安全时，我们以每一时刻行人与车辆的冲突量多少来反映，智能体通过学习减少冲突量来保障行人安全。在评价车辆通行效率时，评价指标为每条道路上车辆的平均速度。

综上所述，本文充分考虑行人安全和车辆通行效率存在的矛盾及行人与车辆不同行为所带来的不同经验，定义奖励函数如下所示：

(10)

1.3.4 基于行人安全的交通信号灯控制模型

本模型综合考虑了交叉口行人安全和车辆效率，通过共享行人与车辆状态，赋予路口智能体更为广阔的观测视野，同时，采用优先经验回放提高采样效率，加速算法收敛，使智能体能够通过观测的全局状态及时调控自身策略，导出全局最优Q值，基于行人安全的交通信号控制结构如图2所示。

图2 基于行人安全的交通信号控制结构示意图

每一回合开始，读取相同的行人与车辆流量文件，以一个周期为频率更新信号配时。当前Actor网络的输出确定下一周期的时长、相位顺序及相位持续时间。当一个周期结束以后通过目标Actor网络和目标Critic网络的输出值函数与当前Critic网络输出的值函数计算出TD误差，并按概率大小存储到优先经验回放池，当前Critic网络从优先经验池中按概率抽样更新，进而指导当前Actor在下一时刻作出包含更少冲突量和更高车辆效率的配时方案，以不断完善策略，如此循环直至达到最终仿真时长。基于行人安全的交通灯智能控制模型伪代码如算法1所示。

算法1基于行人安全的交通信号灯控制模型

初始化：随机初始化当前Actor 神经网络μ(st|θμ)和当前Critic 神经网络Q(s,a|θQ)，初始化目标网络μ′和Q′，记忆库R和高斯噪声N。

算法：

1)for episode = 1, M do：

2)在SUMO平台上导入行人与车辆流量文件

3)随机初始化分布N用作动作探索

4)初始化初始状态s0

5)for step = 1, 10800 do：

6)Actor 网络获取当前路口行人与车辆冲突量

信息和路口车辆通行速度信息，并根据当前的策略选取动作传递给交通信号灯执行，即ai=μ(sj|θμ)+N

7)Actor网络将获取的路口行人与车辆数据

(si,ai,ri,si+1)存储在记忆库中,以作为网络训练学习

的数据集。

8)计算记忆库R中样本抽样概率

9)pi=|δ(t)|+ε

10)将搜索得到的优先级p与样本数据相对应,作

为当前Actor网络和当前Critic网络的训练数据

11)yi=ri+γQ′(si+1,μ′(si+1|θμ′)|θQ′)

12)记忆库存储满后对方差进行0.999的缩放

13)根据公式(3)更新当前 Actor 网络

14)根据公式(4更新当前Critic网络

15)更新目标网络

16)θμ′←τθμ+(1-τ)θμ′

θμ′←τθμ+(1-τ)θμ′

17)end for

18)end for

2 仿真实验

2.1 仿真环境与参数设置

交通仿真环境采用SUOM1.9.0(simulation of urban mobility，城市交通仿真)搭建，并利用TraCI接口完成与算法的在线交互。算法环境采用python3.6.6+TensorFlow1.1.2搭建完成。

2.1.1 单路口属性设置

针对单路口进行仿真分析，道路为4车道，每条路长150 m，从里到外分别为：左转或直行，直行，右转，人行道。其中车道限速为34 km/h，人行道限速为1 m/s，人行横道速限速为1.3 m/s。在仿真中不考虑车辆右转的情况。

2.1.2 交通灯初始属性设置

交通灯属性设置按SUMO官方推荐四车道设置，具体见表1。

表1 交通信号灯初始相位设置

2.1.3 流量设置

车辆和行人的到达服从泊松分布，根据在不同时间段更改车辆和行人到达概率有效模拟出“早高峰”、“晚高峰”和“超低峰”等场景，从而反映出一天内真实的流量环境。将一天的交通流量进行压缩至3个小时(10 800 s)进行仿真实验。分为0～1 350 s，1 350～3 150 s，3 150～4 050 s，4 050～5 400 s，5 400～6 300 s，6 300～7 650 s，7 650～8 550 s，8 550～10 800 s共8个时间段对流量进行统计。各时间段内的到达流量如图3所示。车辆随机进入交叉口的入口并提前选择所在车道，驶出路口时随机选择目标车道，行人随机进入交叉口的入口，直行通过路口。

图3 车辆与行人流量分布柱状图

2.1.4 参数选取

神经网络参数及其余参数选取参考文献[18-19]，实际使用中根据学习情况作适当调整，具体参数如表2和表3所示。

表2 神经网络参数

表3 其余参数

2.2 对比方案分析

为了测试模型的有效性，将本文方法与以下方法进行对比。各方案配备相同的路口属性和行人与车辆流量，如2.1.1和2.1.3所示。

1)固定配时方案。交通灯的相位及相位持续时间设置如2.1.2节，方案中利用SUMO的TraCI接口直接获取每一时刻行人与车辆冲突量，车辆的平均速度等数据来反映路口车辆通行效率和行人安全度。

2)DQN算法配时方案[20]。状态设定为路口车辆位置-速度矩阵和行人位置-速度矩阵；初始动作设定为每个子阶段10 s，学习后智能体根据路口流量动态地改变相位持续时间(可以为0 s)；奖励值函数设定同行人安全配时方案保持一致。方案中相关参数设置见表4所示。

表4 DQN配时方案相关参数

2.3 实验

为了验证本研究的有效性和可用性，需要进行仿真实验回答以下两个问题：

问题1：本研究是否能够提高行人安全性？即在相同的实验环境下与对比方案相比，平均冲突量是否有明显降低？

问题2：本研究是否兼顾了行人安全和车辆效率？即在相同的实验环境下与对比方案相比，路口的总体性能如何？

强化学习中学习率的选取至关重要，实验设计验证前先进行学习率的确定，然后进行对比实验。

2.3.1 PRE-DDPG算法学习率选取

图4描述了单路口下基于行人安全配时方案在不同学习率下的收敛结果。从图4中可以看出学习速率过大或者过小都可能带来性能的损失。当LR-A=LR-C=0.000 001时，算法表现出较好的性能优势。因此在本小节后续的仿真中，算法学习率均选择LR-A=LR-C=0.000 001。

图4 不同学习率的行人安全配时方案训练过程中回合奖励值性能对比

2.3.2 实验设计及结果分析

为了回答以上2个问题，本小节进行了如下实验设计：

1)针对问题1，进行对比实验1：

为了验证交叉口行人安全是否得到提高，即各配时方案中行人与车辆的平均冲突量情况，在同一实验环境下将所提行人安全配时方案与其它对比方案作对比实验。

(1)各配时方案行人与车辆平均冲突量对比

图5即为各配时方案中行人与车辆的平均冲突量对比。从图5可以看到，在相对于其他配时方案，基于学习的配时方案能够根据人流量、车流量的情况实时地调整最佳配时方案，有效地减少行人与车辆的相互冲突。相对于DQN配时方案，我们所提出的行人安全配时方案平均冲突量为0.66，减少了16.40%的行人与车辆的事故率，有效地改善了行人过马路的安全性。

图5 行人与车辆的平均冲突量对比

2)针对问题2，进行对比实验2：

为了验证所提行人安全配时方案的总体性能，在同一实验环境下对各方案作摘除行人因素的对比实验。

1)考虑行人安全下，各配时方案车辆平均速度对比。

图6为各配时方案中车辆在平均速度的对比情况。从图中可以发现，本文所提出的方案在平均速度性能上优于对比方案，特别是在高峰车流量下(例如，时间段3)。通过对各时段的数据进行平均处理，我们可以得到行人安全配时方案中每条道路上车辆平均速度为21.40 km/h。相对于DQN配时方案均速度提高了40.28%，相对于固定配时方案平均速度提高了29.62%，车辆效率有效得到改善。同时可以看到，DQN配时方案相对于固定配时方案车辆平均速度减少了5.40%，平均冲突量减少了64.04%，可以明显看出DQN配时方案为保证行人安全通过交叉口牺牲了一定的车辆通行效率。

图6 车辆平均速度性能对比

2)摘除行人因素前后，各配时方案车辆平均时延对比。

为了更好地比较各方案中行人因素对车辆效率的影响，分别对各方案作摘除行人因素的对比实验。图7为各方案中每条路上车辆平均时间延迟的对比情况。时间延迟为车辆实际行驶时间与最大行驶速度行驶时间的差值。从图7可以看到各配时方案中行人因素对于车辆效率的影响：

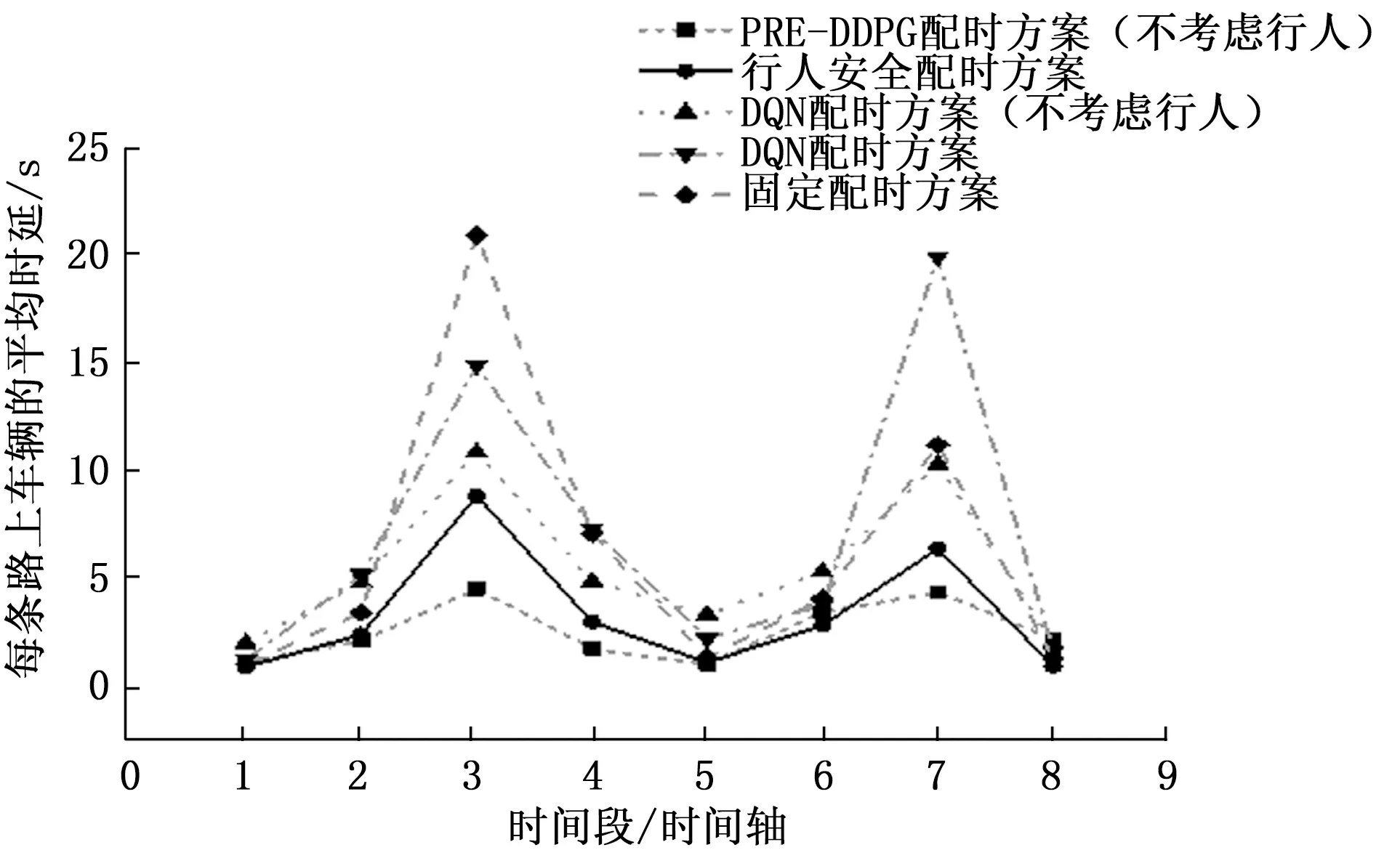
图7 车辆平均时间延迟对比

(1)将行人安全配时方案和DQN配时方案分别做摘除行人因素前后车辆平均时延对比，得到所提行人安全配时方案由不考虑行人时的车辆平均时延2.59 s增长到3.32 s，DQN配时方案由5.46 s增长到7.05 s。可以看出，交叉口考虑行人安全会对车辆效率产生一定的负面影响。

(2)尽管考虑行人安全会对车辆效率产生一定的负面影响，但所提基于行人安全配时方案在兼顾行人安全和车辆效率方面，优势仍然比较明显。对比车辆平均时延可以看到，行人安全配时方案相对于DQN配时方案(不考虑行人)有39.16%的提高，相对于DQN配时方案有52.90%的提高，相对于固定配时方案有47.54%的提高。

3 结束语

提出了基于行人安全的交通信号灯智能控制方案，折中考虑行人安全与车辆通行效率，实现系统效用的最大化。相对于传统配时方案，所提方案考虑行人因素并且自适应性强，能够在连续强大的交通环境中提取合适的特征，选取合适的动作。研究结果显示，该算法模型具有较好的收敛性，在兼顾行人安全和车辆效率上都明显优于固定配时方案和DQN配时方案。本文仅考虑了单路口时行人和车辆问题，没有做多路口的情况，下一步的研究主要集中在多路口协调下的行人和车辆问题。