基于EEMD模糊熵和PSO-KELM的NPC三电平逆变器故障诊断

马子旸，张朝龙, ，何怡刚

(1.安庆师范大学 电子工程与智能制造学院，安徽 安庆 246052;2.武汉大学 电气与自动化学院，武汉 430072)

0 引言

NPC三电平逆变器的输出电压高且容量大，产生的电流谐波含量少，工作效率高，因此近些年来广泛应用于新能源发电及电能贮备系统中。NPC三电平逆变器的电路拓扑结构较普通逆变器更为复杂，其功率开关器件频繁地闭合关断，易发生开路故障，会引起系统中电力电子器件的过饱和问题，产生的过高电流会损坏设备，存在着极大的安全隐患。为了避免故障对系统的正常运行造成影响，选择合适的故障诊断方法对于提升系统的稳定性，保证系统可靠性方面至关重要。

传统的逆变器开路故障诊断策略通常单一的依靠信号处理的方法，主要体现在通过获取开关管开路故障时刻的电压或者电流信号来提取相关信息。三相电流与克拉克变换相结合，得出电流的运行轨迹，从而判断故障发生的位置[1-2]。通过提前设定电压残差的相关阈值，来检测并判断IGBT的故障部位，实现快速定位[2-3]。但上述所提及的传统方法易受到外界干扰信号的波及，且对采集信号的纯度要求较高，依赖性强，所以故障准确率较低。

现有的逆变器开路故障诊断策略更多是基于信号提取和机器学习方法相结合，当故障发生时，对系统的故障信号进行识别分类及定位。傅里叶变换可以有效地提取出逆变器电压信号的频域和时域特征，但是只能在单一范围内取得成效，故无法全面提取故障信息。小波分析和概率神经网络(PNN, probabilistic neural network)相结合，稳定性高，但输入端的测量信号未进行去噪处理，故诊断速率一般。主成分分析(PCA, principal component analysis)加上支持向量机(SVM，support vector machine)[4-5]，针对混杂系统取得了良好效果，但不同故障状态下的模型参数难以抉择。经验模态分解(EMD, empirical mode decomposition)[6-7]将原本复杂的故障信号分解成若干段本征模态分量(IMF, instrinic mode function)作为故障特征值进行分析，化繁为简，但EMD在递归式分解的过程中存在模态混叠从而可能导致误诊[8-9]。

但是目前针对逆变器开关管器件开路故障的研究进展依然不够全面可靠，故本文提出一种基于EEMD模糊熵和PSO-KELM的故障诊断方法[10-11]，EEMD在EMD基础之上加以改进，具有很强的抗模态混叠能力。模糊熵则对电压信号的波动畸变具有很强的敏感性，将二者结合可以及时检测出逆变器系统的电压突变。KELM是由极限学习机(ELM， extreme learning machine)优化改进而来[8-9]，在保留ELM学习速率快和泛化性强的基础上，核函数的加入再加上粒子群优化使得KELM的稳定性大幅提高，在信号处理过程中分类性能较好。

鉴于现有的研究工作与进展，本文在Matlab/Simulink平台搭建NPC三电平逆变器仿真模型，采样电压信号，利用EEMD先将原始信号处理成若干段稳定的IMF模态分量和一个余项，经相关系数法准则去除掉作用小的分量，然后计算剩余IMF分量的有效模糊熵值，形成能表征不同类型开路故障时刻的特征向量，通过优化过的PSO-KELM进行分类，最终可达到较高的故障诊断准确率。

1 诊断方法理论介绍

1.1 模糊熵的特征提取

模糊熵使用隶属度函数和均值算法作为度量判据，将故障特征向量作为样本信息，模糊相似度量后进行有效分类，可解决其他类型熵划分故障特征在时间序列尺度上过于单一的问题，且较为稳定。模糊熵利用指数函数(模糊函数边界的梯度是为n,宽度是为r)来计算向量之间的相似性，对于一段若干个序列点排列成的时间序列，模糊熵的计算公式如下：

先对时间序列处理得到m维向量，即是:

(1)

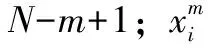
随机定义两向量之间的间隔为两者所对应元素绝对值的最大差值，即是：

max{[x(i+k)-u0(i)]-[x(j+k)-u0(i)]}-

[x(j+k)-u0(j)]}

(i,j=1,2,...N-m,i≠j)

(2)

定义模糊函数是为：

(3)

模糊匿度函数在m+1维上的形式如下：

(4)

式中，r表示函数的相似容限。

由以上这些步骤可以得到模糊熵值是为：

FuzzyEn(m,n,r)=

(5)

在N为具体的有限数字时，得到模糊熵的数学表达式如下：

FuzzyEn(m,n,r,N)=lnψm(n,r)-lnψm+1(n,r)

(6)

1.2 EEMD方法

EEMD是利用高斯白噪声独特的时频域特性，将其与原始信号相结合，经过多次分解得到所有的本征模态分量后对其取均值，因为高斯白噪声能够保证每个模态分量在时域中的有序性，使得不同的时间尺度信号匹配到适宜的参考尺度上，从而在一定程度上消除模态混叠，算法具体过程如下：

确定信号x(t)并添加标准差为常数，均值为零的高斯白噪声ni(t),则公式如下：

x(t)=xi(t)+ni(t)

(7)

信号xi(t)进行EMD分解得到若干个IMFs分量cij(t)与一个剩下的残留分量ri(t)。

重复一二两步共H次，进行总体平均以消除高斯白噪声的影响，得到EEMD分解的第j个IMF分量：

(8)

因为在上述迭代计算的过程中，分解产生的一些误差客观上将会影响到最终求得的IMF分量的准确性，不是所有的IMF分量都可以代表原始信号的相关特征，所以有必要去除掉无效的IMF份量。可以通过计算相关系数来确定：

(9)

式中，原始信号x与IMF分量ci的协方差为Cov(x,ci),原始信号x的方差为D(x)。Puci的取值范围是为[-1,1]，[0,1]表示的是正相关，[-1,0]则表示负相关。相关系数的绝对值大小反映了分解得到的本征模态分量和原始信号的线性相关度，绝对值越大，相关度越高，有效性则越强。

使用EEMD分解得到特征提取后的模糊熵IMF分量，并适当剔除一些无关分量，即为EEMD多尺度模糊熵。

1.3 基于PSO-KELM的故障识别

通过EEMD模糊熵有效提取故障信息后，要根据故障的不同类型来进行划分，本文采用核函数极限学习机进行故障识别。ELM属于单隐层前馈神经网络(SHFNN, single hidden feedforward neural networks),其优势在于不需要人为调整隐藏层的偏置和权重，可以随机生成，但其结构则相对较为简单，故引入核函数来提高性能。

ELM的输出函数如下：

(10)

式中，h(x)是对应输入样本x的隐藏层输出，是隐藏层和输出层之间的输出权重向量，H是隐藏层输出矩阵。

定义KELM的核矩阵为：

ΩKELM=HHT:ΩKELM=h(xi)h(xj)=KKELM(xi,xj)

(11)

由上面二式可得到KELM的输出函数为：

(12)

1.4 PSO优化KELM步骤分析

粒子群算法是研究人员观察鸟类铺食过程中相关群体以及个体运动规律的所归纳总结出的优化算法。从微观粒子运动的角度出发，针对解空间的可行域中每个粒子以及对周围粒子的搜索能力，动态调整其具体的空间位置和运动速度，粒子的适应度函数依赖于局部极值P和整体极值G的变化，并在优化迭代时不断更新，具体的计算公式如下：

Vid=ωVid+C1random(0,1)(Pgd-Xid)+

C2random(Pgd-Xid)

Xid=Xid+Vid

(13)

式中，ω为惯性因子，其数值的变化可以改变局部寻优与全局寻优的结果。C1和C2则分别表示个体学习因子的加速常数和社会学习因子的加速常数，random(0,1)则表示取0～1之间的随机数。

在使用粒子群算法优化核函数极限学习机的过程中，将PSO的优化参数与KELM的隐层偏差与输入权值相结合，使用KELM学习样本的期望输出和实际输出的均方差误差作为PSO的适应值，不断地优化迭代，动态更新每个粒子的位置和速度，当算法逐步运行到最大临界值，此时种群的最大个体数即是最优个体，以此往复训练，最后即得到粒子的真实输出。由以上分析，可得出PSO优化KELM步骤的算法流程如图1所示。

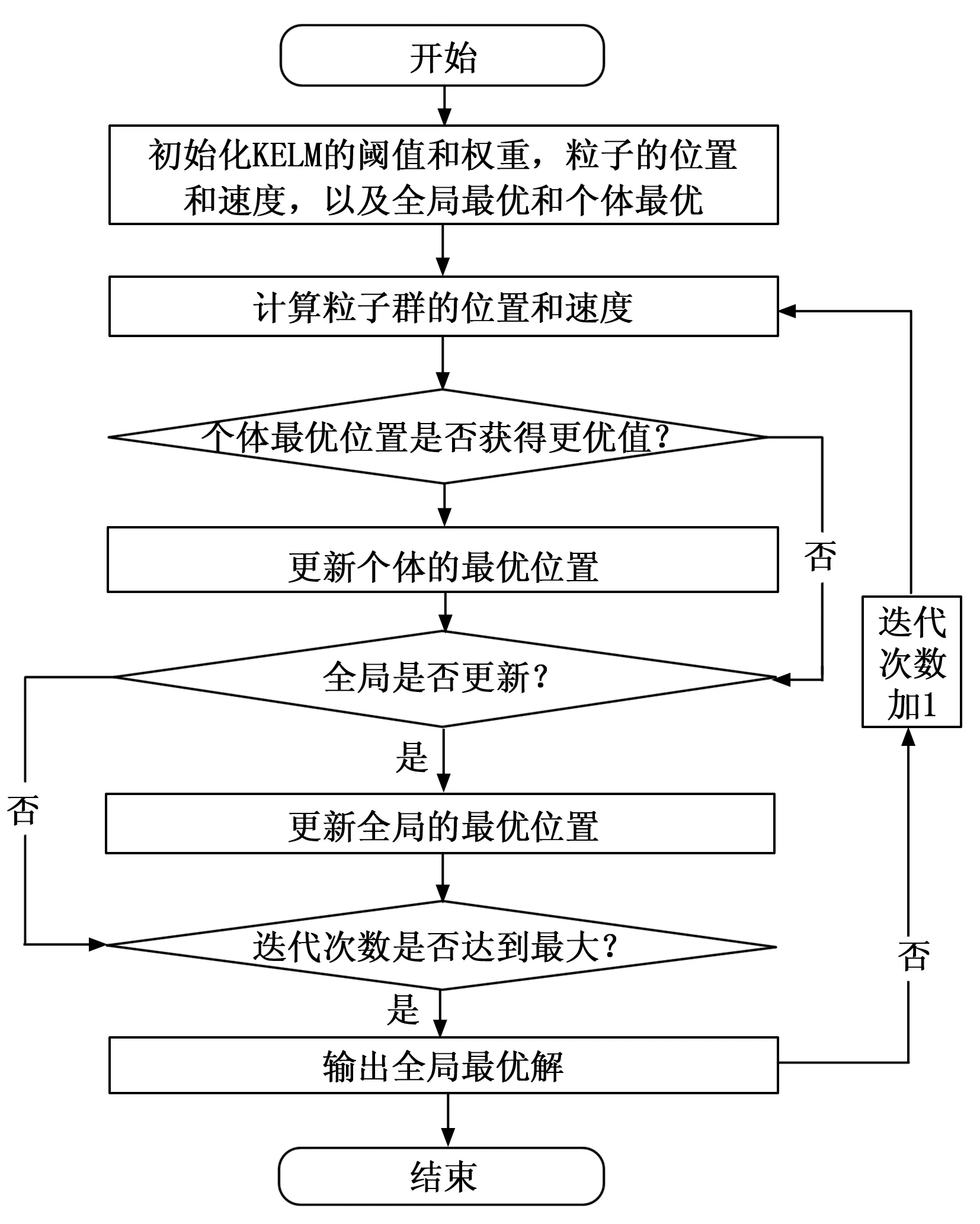
图1 PSO优化KELM过程

先初始化PSO的基本参数，然后通过比较粒子的特征选择阈值和权重，从而得到粒子选择的特征个数和特征输入，再结合KELM参数值建立故障诊断模型，对粒子的个体适应度确定后，更新局部极值P和整体极值G，进而更新每个粒子的位置与速度，重复以上步骤直到实现最大迭代次数，输出KELM分类器和分类结果。

2 仿真实验分析

基于EEMD模糊熵和PSO-KELM的诊断流程如下：1)在MATLAB/SIMULINK平台上搭建NPC三电平逆变器仿真模型，设置各种开路故障状况；2)采样逆变器输出端各类故障状态下的三相电压信号，并对其作归一化处理；3)将采样好的电压信号，通过EEMD进行本征模态分解，得到若干个固有的模态分量，再通过观察图像和相关系数法选取有效的IMF分量，求取其相关的模糊熵，即是EEMD模糊熵；4)将求解得到的所有EEMD模糊熵作为特征向量矩阵集划分为训练特征向量矩阵集和测试特征向量矩阵集；5)建立KELM模型，并用PSO对其优化；6)将待测的训练特征向量矩阵集和测试特征向量矩阵集输入到优化好的PSO-KELM分类器中，进行故障识别，确定开关管以及相关器件的工作状态与故障情形；7)故障诊断后输出结果，诊断率良好，表明该诊断方法切实可行。

2.1 电路模型及其故障情形分析

NPC三电平逆变器的拓扑结构如下：

主电路结构由a,b,c三相桥臂组成，每相桥臂上包含2个钳位二极管，4个功率开关器件与续流二极管组成的电力电子设备，每一相电路由中性点相连，并在负载中性点(N点)处交汇，呈三相三线制，总共包含12个以IGBT开关管为主体的电力电子器件，桥端的输出电压通常有正电压，0以及负电压。钳位二极管作为中点用于连接直流侧电容器与电源开关，LCL滤波器则用于滤波从逆变器中输出的三相电压用于为系统供电。门信号作为驱动电源开关状态的方式，电源打开时门信号为1，当电源关闭时门信号则为0，本文采用传统的PWM调制策略来控制门级信号，从而决定逆变器的开关模式。

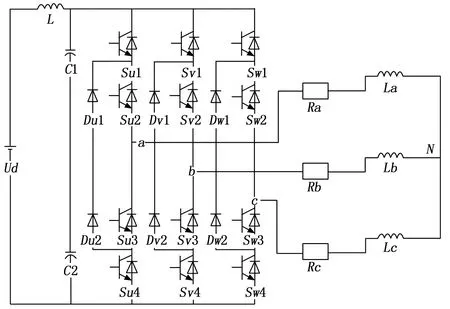
图2 逆变器主电路拓扑

在运行过程中，由于逆变器所处复杂的工作环境，且频繁的开通与关断，所以其中的开关管及相关器件发生故障在所难免，故障可分为短路故障和开路故障，由于电路自带保护电路，所以短路故障往往影响不大，而开路故障则因为相位开关器件所处位置的差异，以及受损数目有所不同，会造成逆变器整体输出的电压值紊乱从而影响系统的稳定运行。故障种类纷繁复杂，通常情况下，3个及其以上数目的开关器件同时发生故障的概率极低，本文不作讨论，因模型有12个IGBT开关管，故单一发生故障的情形有12种，同一相桥臂上两开关管同时发生故障的情形有12种，交叉桥臂上两开关管同时发生故障的情形为36种，上中下3个桥臂连同中性点之间构成3种故障情形，将正常工作状况也视为一种特殊的故障情形，总计64种故障情形，因为NPC三电平逆变器在拓扑结构上符合严格的三相对称，避免实验数据重复训练测试，经灵敏度测试，可得知实际故障有22种，为了便于区分对其进行5位二进制编码，如表1所示。通过采样各故障情形的三相电压值作为故障诊断的特征信号进行分析。

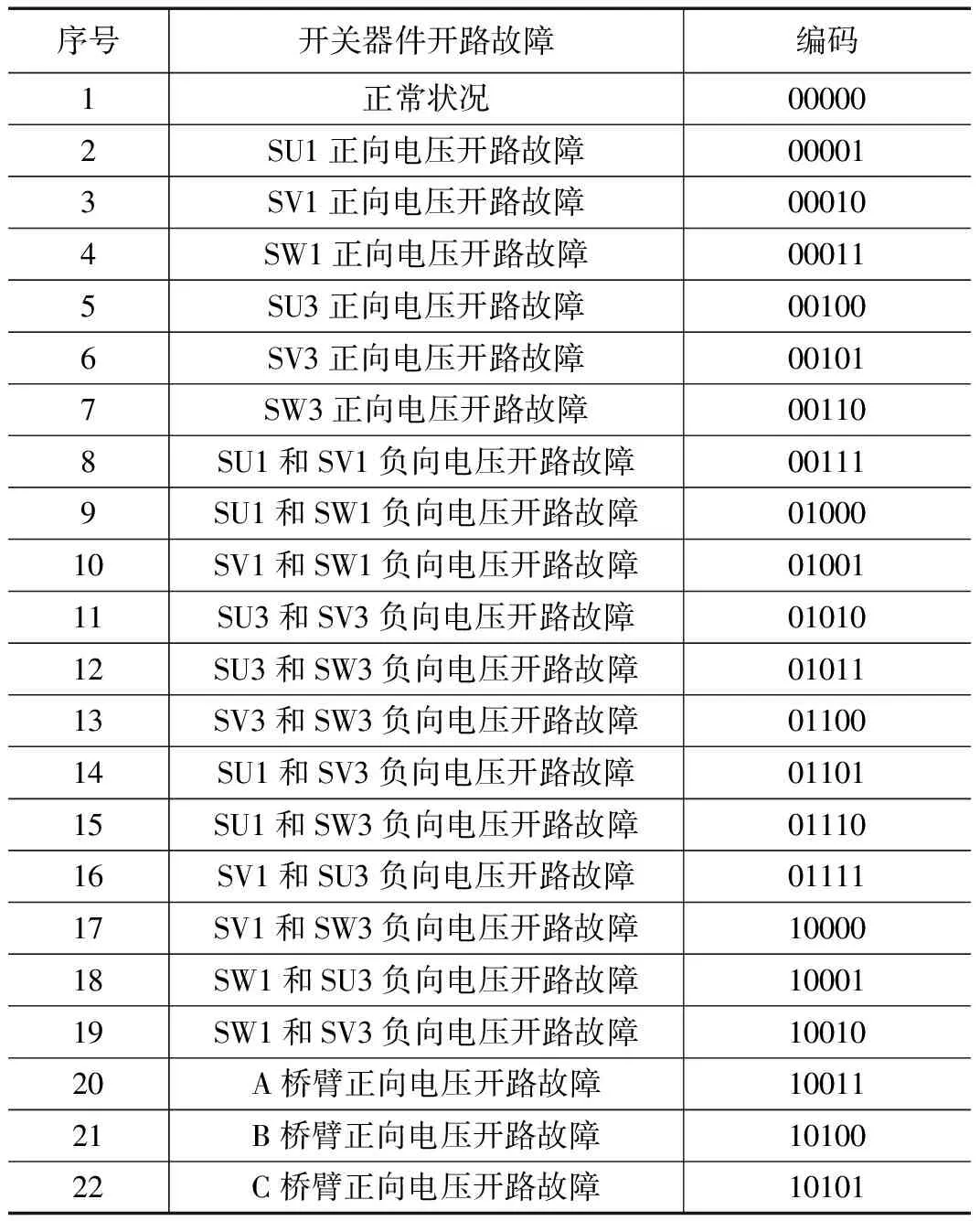
表1 故障情形及5位二进制编码

2.2 故障特征提取

采样时间设置为1 s，每类故障电压信号的单次采样点为1 000个，为了确保实验的客观有效性，减少可能存在的实验误差，对数据样本统一做归一化处理。对所有的故障电压信号样本采集完之后，通过EEMD将其逐一分解成若干段本征模态分量，因有22种故障情形，故单列出SU1故障时刻的电压信号分解结果作为典型代表，设置辅助的白噪声的标准差为原始标准差的0.2倍，设定迭代次数M=100,图3为SU1开关管开路故障时刻电压信号EEMD的分解结果。

由EEMD分解图可见，EEMD分解的电压故障信号逐次从高频到低频分解出8个IMF分量和一个余项，IMF1到IMF6所包含的有效信息较之IMF7和IMF8要多，且通过计算相关系数，可以得知前面部分的IMF与原始信号相似度高，因此选取前6个高频IMF分量更加能够达到准确表征原始信号的目标，列出SU1管剔除无效分量后的IMF分布情况，同理可得出其他21种情况的有效IMF。

根据多尺度模糊熵的计算步骤，选取前6个IMF分量，设置嵌入维数m为4，相似容限r为0.2 SD，模糊函数的梯度n选取为3。由多尺度模糊熵的计算公式，对该模态分量可以得出其相关的EEMD模糊熵，构成的矩阵维度为1×3。由此推广，对22种故障情形分别叠加100次的高斯白噪声，将计算得到的模糊熵进行排列组合，最终得到22×100×1×3维度的矩阵作为故障特征向量，为了对各类故障进行合理的区分，将EEMD模糊熵提取得到的数据样本集做三维投影，箭头EE表示每一类故障的具体分布，如图4所示。

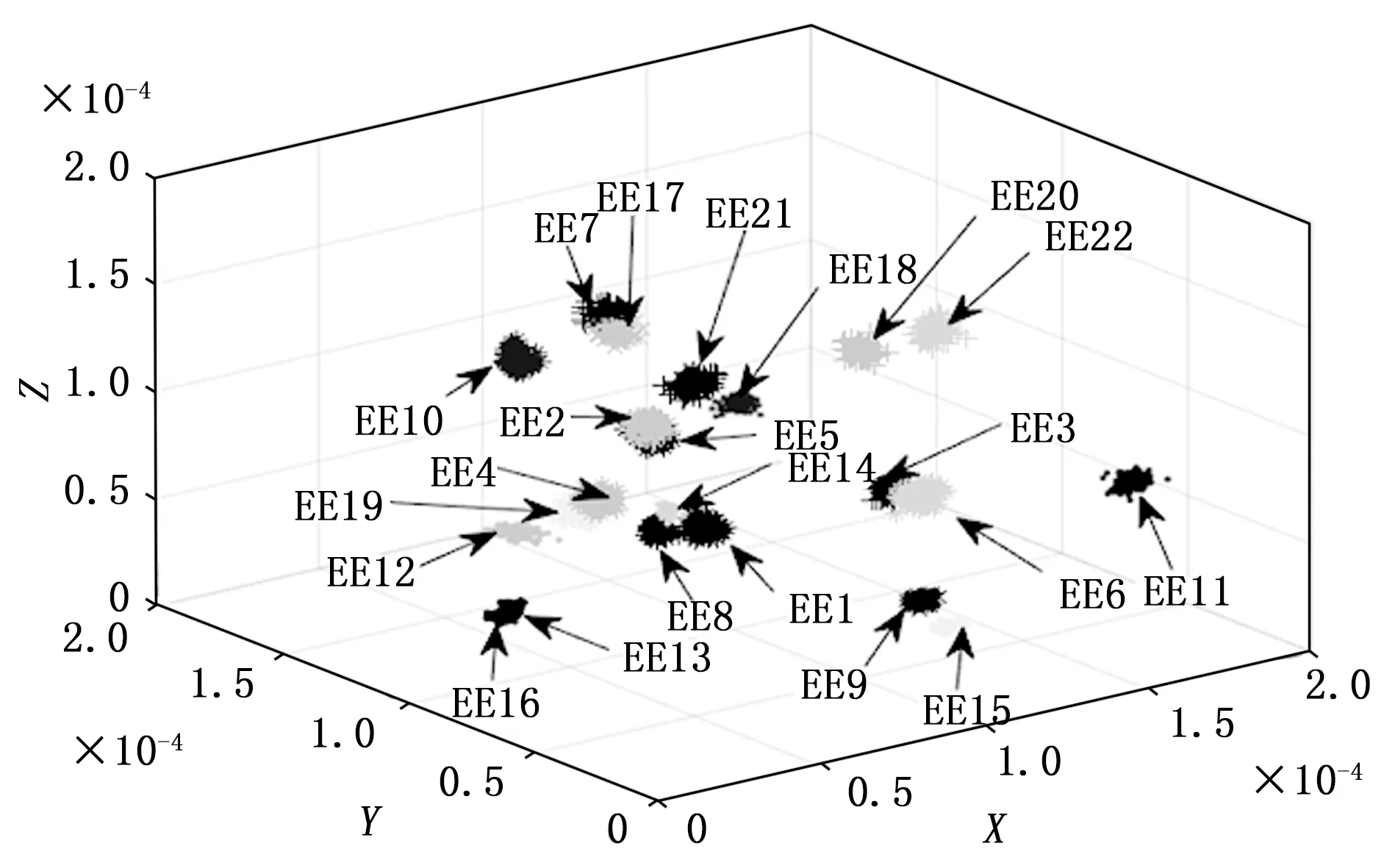
图4 EEMD模糊熵分布

由图4观察，不难发现各类故障所对应的EEMD模糊熵有着明显的区分度，存在较大差异，适用于后续分类器模型的训练和测试。

2.3 基于PSO-KELM的故障分类识别

经过模糊熵的计算后，将所有故障情形下的EEMD模糊熵的值作为特征向量矩阵集，故障类型有22种，故设置22个故障标签依次标记为1～22，每种故障为100组1×3的数据，可得总数据集为2 200。首先将数据集划分为训练特征向量矩阵集和测试特征向量矩阵集，随机选取每类故障的前50组数据依次叠加22次组成总计1 100组数据集作为训练特征向量矩阵集，同理划分剩余的数据集作为测试特征向量矩阵集使用。把训练特征向量矩阵集输入到PSO-KELM分类器中，对其进行训练，完成故障诊断模型的建立，将测试特征向量矩阵集输入到故障诊断模型中，测试相关的准确率，最后的分类结果作为评价分类器优劣的性能指标。

本文使用PSO对KELM进行参数优化和验证利用PSO可以提高对故障数据集的搜索能力和延展性。设置PSO的相关参数，个体学习因子加速常数c1初始值为1.5，社会学习因子加速常数c2初始值为1.7，迭代次数G=100，终止代数pop=20。令KELM分类器的隐层神经元节点的个数为L，选取L=20，设置KELM的核函数类型为径向基核函数(RBF kernel，radial basis function)，最为重要的两个实验参数分别是核函数参数g与正则项系数c，通过对KELM的多次训练，根据实验数据的对比，得出最优的核函数参数g为8.883 94e+06，最优正则项系数c为93.490 4。实验测试结果如图5所示，此时PSO-KELM的分类效果达到最佳，故障诊断的测试精度达到98.454 5%，实验结果理想，表明该方法切实可行，分类效果较好。

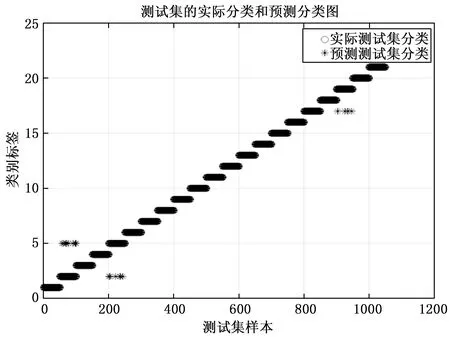
图5 PSO-KELM模型诊断结果

为了避免PSO-KELM在实验过程中所实现的诊断率存在偶然性，故对此进行10次独立实验，并且统计如表3所示。

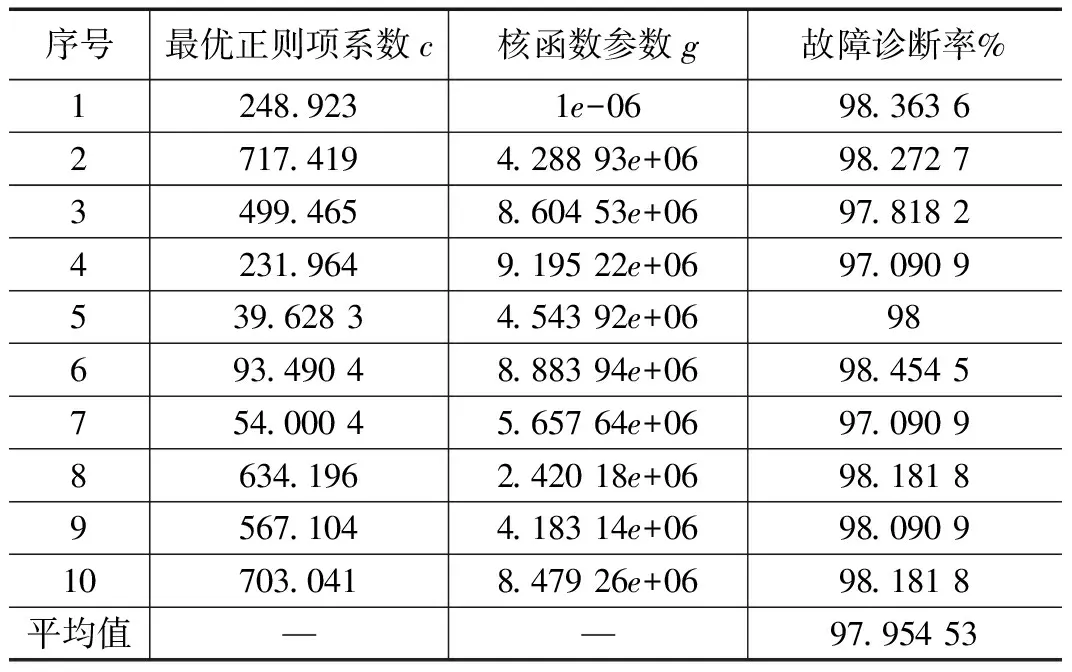
表3 PSO运行适应度曲线

总体来说，PSO方法在减少了更多的训练时间前提下，且保证了KELM能够选择更少的训练特征向量矩阵集时，依然能够保证较高的故障诊断准确率。图6表明了PSO独立运行10次后统计得到的诊断率以及相对应的诊断率的平均值情况。

图6 PSO-KELM运行10次的结果

验证本文提出的基于EEMD模糊熵和PSO-KELM诊断方法的客观性与准确性，在仿真实验中，将进行过特征提取的EEMD模糊熵输入到随机森林(RF，random forest)，SVM这两种分类器中，再使用模糊熵提取故障特征向量，输入到上述两种分类器和PSO-KELM中，划分相同形式的训练集和测试集，在完全一致的实验条件下进行对比分析，不同的故障诊断方法的诊断结果如表4所示。

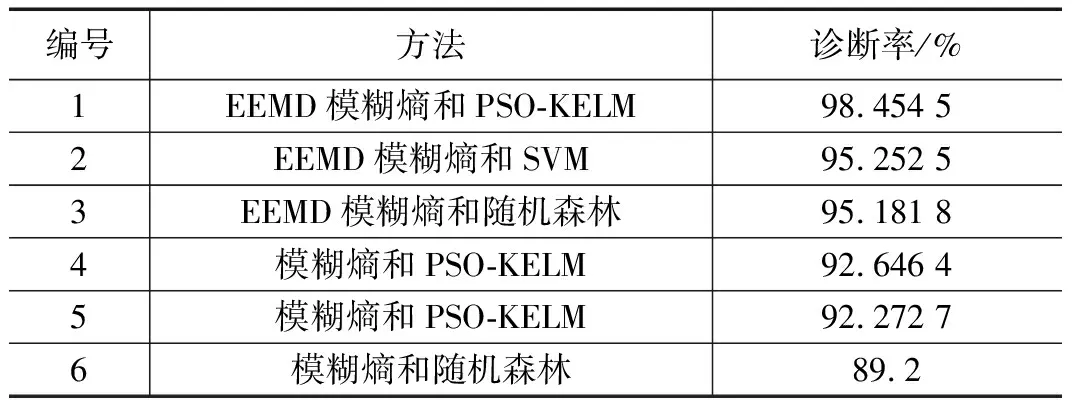
表4 故障方法性能对比

与其他诊断方法的比较中不难得出，EEMD模糊熵与PSO-KELM相结合的故障诊断率优于其他方法，说明其提取的故障特征向量区分度更高，分类器的实验效果更为准确，可以客观全面的反映NPC三电平逆变器的开路故障状态。

3 结束语

本文提出一种基于EEMD模糊熵和PSO-KELM的针对NPC三电平逆变器单一器件开路以及多器件同时开路的故障诊断方法。通过采样NPC三电平逆变器的多路电压信号，使用EEMD模糊熵进行故障特征提取，归一化后得到实验数据集，将其输入到PSO-KELM中。诊断结果表明，算法的数据搜索性能强大，延展性好，易于实现，训练测试得到最优的故障诊断率为98.454 5%，故障识别精度较好。在相同的实验条件下进行对比实验分析，诊断能力均优于其他方法，且适用于多类故障情形，抗噪声能力强，符合NPC三电平逆变器的在线诊断要求。