基于改进差分进化算法的热电池装配机器人优化设计
何玲,钟江川,张钦仰
(贵州大学 现代制造技术教育部重点实验室,贵阳 550025)
工业机器人具备工作空间大、结构紧凑、柔性好、成本低等优点[1],广泛应用在智能制造领域。精度是衡量机器人性能的重要指标,精度的提高将使机器人在智能装配中有更优秀的表现[2]。日趋复杂的工业产品结构对智能装配控制精度的要求越来越高,热电池组通常由若干单体热电池串并联形成,受总体结构等条件限制,就出现了异形热电池组,增加了机器人装配难度[3]。智能制造装配过程中装配精度要求高,装配环境复杂,装配的可视化程度低,为装配带来较大的难题[4]。
热电池具有比能量和比功率高、激活迅速可靠、适应环境能力强、贮存时间长、结构紧凑、工艺简便、生产成本低、免维护等优点,成为航天的首选电源[5-6]。随着航天技术的进步,对电源系统的要求也越来越高[7],为满足电源系统的要求,通常将若干单体热电池排列串(并)联形成热电池组。受到应用场景的影响,热电池有许多形状、尺寸不一的结构,这就导致热电池装配顺序复杂、不统一,并且航天器内部装配空间小,可视化程度低。这些都要求机器人在装配过程中有精度高、智能化程度高的能力。
为发挥机器人在装配中高精度、智能化的能力,季旭全等[8]针对星载设备装配空间半封闭、可视化程度低的问题提出了一种基于机器人与视觉引导的智能装配方案,该方案提高了装配效率,但在装配过程中未考虑实际装配空间。胡瑞钦等[9]针对大型航天装备提出了一套基于力/位移的机器人柔性装配方法,该方法虽成功应用于多类航天器大部件装配中,但是在装配过程中力感知与力控制精度方面还需进一步优化。陈雨杰等[10]得出一种利用机器人自动绘制基准标定、工艺标识等进行辅助装配的方法,这些装配方案主要研究的是可行性问题,缺乏对装配精度问题的关注。
为了提高机器人的精度,范文强等[11]针对LED装配位置精度无法保证的问题提出了一种基于待装配孔位姿测量的装配轨迹在线修正方法,该方法虽成功解决了工业机械臂运动误差,提高了自动装配的实际生产效率和精度,但该方法并未分析、考虑待装配工件的实际位置与工业机械臂预编译装配轨迹之间的偏差。顾岩等[12]针对狭小空间内虚拟手臂运动规划求解难等问题提出了一种运动学与动力学结合的分层求解优化方法,该方法提高了手臂路径生成效率以及装配精度,但只适用于自由度低于3 的机器人。何启嘉等[13]提出了一种解析法求解部分解、自适应多种群的遗传算法求解其余解的机器人逆运动求解方法,该解析法求解精度高,但求解必须满足Pieper 准则,实际应用性较差。谢习华[14]、李清[15]和Mao[16]等采用优化差分进化算法求解机器人逆运动学问题,该算法求解稳定性高,但在设置姿态误差和位置误差权重时采用经验值,主观性较强,没有考虑机器人运动学特性。
针对异形热电池装配,文中设计一种装配机器人。通过改进D-H 参数法构建机器人连杆参数坐标系,对机器人进行运动学建模,结合机器人运动特性分析姿态误差和位置误差的关系,利用改进差分进化算法求解装配机器人。
1 装配机器人工作原理
热电池组的装配任务多为紧固螺钉,所用的螺钉会随着热电池组的大小而发生改变,且热电池组的大小、形状各不相同。较大的热电池组四周会有单个热电池,因此需要装配机器人伸展空间大、灵活性好。考虑到机器人自身误差和螺钉尺寸误差,得出机器人末端误差不超过螺钉公称直径1%的结果。热电池组装配使用M2 的螺钉,因此热电池组装配误差最大不超过0.02 mm,见图1。
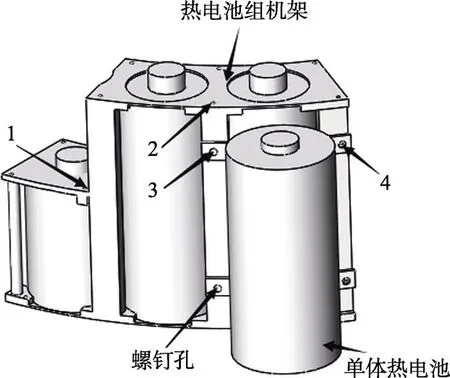
图1 热电池组三维模型Fig.1 3D model of the thermal battery
根据热电池组装配的特点,设计了六轴关节型机器人,见图2。该机器人由6 个转动关节串联而成,机器人主体由机器人底座、机器人底座旋转关节、大臂、小臂、手腕和末端法兰盘构成。机器人底部旋转关节360°旋转控制机器人横向工作,调整大臂与小臂位姿实现不同高度的热电池装配,轴4 旋转关节控制横向与竖向装配,使机器人实现对热电池四周附着单体热电池的固定。通过调整轴5 与轴6 旋转关节来提高装配精度。较长的大臂与小臂结构使机器人运行空间增大,但是这也对机器人的精度造成巨大影响,悬臂式的结构使得机器人工作时振动较大。

图2 机器人三维模型Fig.2 3D model of the robot
2 运动学模型
使用改进D-H 参数法对机器人构建数学模型,构建连杆坐标系,其中X0、Y0、Z0分别为基坐标系的坐标轴,Xi、Yi、Zi分别为各关节坐标系的坐标轴,见图3。

图3 机器人连杆坐标系Fig.3 Robot connecting rod coordinate system
机器人连杆参数见表1。其中di表示相邻关节之间的连杆长度,ai–1表示相邻关节连杆偏移量,αi–1表示相邻关节坐标系之间的扭转角。θi表示相邻关节的关节角。

表1 机器人连杆参数Tab.1 Robot connecting rod parameters
根据改进D-H 参数法构建杆与杆之间的相对变换通式见式(1)。

式中:sθi、cθi、sαi、cαi分别表示θ与α的正余弦值。机器人末端连杆坐标系相对于基坐标系的关系可由上述各连杆变换矩阵相乘得到式(2)。

式中:姿态矩阵R3×3表示机器人末段连杆坐标系各基准轴相对于基坐标系的位置向量;位置矩阵P1×3表示机器人末段连杆坐标系原点相对基坐标系位置。
按照图1 中的热电池组装配螺钉1、2、3、4 的位置,生成机器人末端轨迹,见图4。该轨迹表示机器人的3 种装配情况,分别为上下来回装配、从热电池组上下两端向热电池组四周装配和同一高度平移装配。根据机器人末端的位姿计算各关节角度值对机器人动态特性分析、运动控制等研究有重要意义。

图4 机器人末端轨迹Fig.4 The trajectory of the end of the robot
3 基于改进差分进化算法的逆运动学求解
DE 进化算法是基于实数编码的一种遗传算法,增强了全局寻优的能力,但也暴露出易陷于局部收敛的缺陷。针对此问题,文中在变异过程中提出了新的自适应算子,在边界处理上提出了边界比例映射法。
3.1 目标函数设计
位姿矩阵分为位置函数与姿态函数,因此可将求逆解问题转化为在变量取值范围内求解函数最值的问题,即为求解的机器人末端执行器的位姿和目标位姿之间的误差函数。由式(2)可知,机器人末端执行器的目标位姿矩阵见式(3)。

式中:Ra表示目标姿态矩阵;Pa表示目标位置矩阵。机器人末端执行器的当前位姿矩阵见式(4)。

式中:Rt表示当前姿态矩阵,Pt表示当前位置矩阵。则目标函数计算公式见式(5)。

式中:α、β为位置误差与姿态误差的权重,为使该求解方法能够适用于其他机器人,设计了权重计算见式(6)。

式中:λi表示机器人各轴连杆长度,Pdi表示各轴连杆偏距,该方法根据机器人的结构引入的自适应权重系数不仅能够平衡两种误差的重要性,还提高了普遍适用性。
3.2 算法流程
1)种群初始化。根据关节转角范围随机生成N组关节角,则初始种群个体计算见式(7)。

式中:rand 表示(0,1)随机取值,且服从均匀分布的小数;Uijmax、Uijmin分别为个体i关节角j取值的上下限;Np=200 为种群大小,i=1,2,…,Np、j=1,2, …,6。
2)变异操作。标准DE 算法的变异控制随机性大,使种群差异大,增大了搜索范围,降低了收敛速度,因此文中在保留原有变异方式的同时,引入当前种群最优个体作为初始量,不仅避免局部最优结果,而且能达到提高收敛的速度。则变异个体的计算见式(8)。

式中:xp1、xp2、xp3为种群随机选择的3 个个体,且p1≠p2≠p3;缩放因子F取值为0.8;xb(t)为迭代t次种群中最好的个体,T=1 000 为迭代次数。
3)边界处理。边界处理多以随机再生成的方式,这样的方式将减少父代与子代间的联系,降低收敛速度。文中采用比例映射法,将边界内的值与边界外的值成比例一一对应,保留变异个体的位置信息,一定程度上削弱了随机性,其边界处理见式(9)。

4)交叉选择。交叉选择在增加种群的多样性的同时,保留了优化的个体。其交叉的计算见式(10)。

式中:交叉概率C取值为0.9。
通过变异、交叉产生的实验体采用贪婪的选择策略,其计算公式见式(11)。

5)终止判断。重复步骤2 至4,使迭代次数达到最大值即终止程序,输出最优解。
3.3 实验测试与分析
为验证上述改进DE 算法的稳定性,进行如下实验:将螺钉1 所在位置的机器人位姿矩阵作为目标矩阵,对该位置进行重复100 次求解实验,实验结果绘制见图5。由图5a 可知,改进DE 算法求解平均迭代次数为219.85 次,比DE 算法平均迭代次数少600次,并且每次求解都能得到最优结果。由图5b 可知,改进DE 算法平均求解时间为5.27 s,比DE 算法平均求解时间少1.8 s,并且2 种算法求解均未出现异常值。表2 为100 次实验结果分析,其中改进DE 算法的最优结果平均值为3.337×10–4,求解时间偏差为0.197,说明改进DE 算法收敛速度较快,且精度更高。综合以上结论表明改进DE 算法具有稳定的求解能力并且求解速度更快。

图5 实验结果统计Fig.5 Statistics of experimental results

表2 100 次实验结果分析Tab.2 Analysis of 100 experimental results
为验证改进DE 算法所求的结果是否优于传统DE 算法,研究如下。
将图4 机器人末端轨迹均分为35 个位姿,分别采用DE 算法与改进DE 算法对这35 个位姿矩阵进行求解,所求结果应为一组关节角度,但为了对比位置与姿态,将所求关节角带入式(2)得到位姿矩阵,其结果如下。
标准DE 算法的平均位置误差约为0.01 mm,姿态误差约为1°,位置误差最大值为0.1 mm,出现不满足装配精度的情况,见图6。改进DE 算法的位置误差约为1×10–4mm,位置误差最小值为1×10–8mm,姿态误差约为1×10–5度,满足装配精度。将上述35个点平均位置误差、姿态误差及迭代次数统计于表3中,改进DE 算法求解平均迭代次数为219.857,相较DE 算法结果降低了600 次,效率提高了72.5%。由计算结果的平均值也可以得到改进DE 算法求解精度高于DE 算法,并且迭代次数标准偏差结果显示改进DE 算法求解效率更高,稳定性更好。综上结果表明改进DE 算法相较于标准DE 算法有更高的精度而且收敛速度更快、稳定性更好,完全满足机器人的精度要求。

图6 2 种算法结果对比Fig.6 Comparison of the results of the two algorithms

表3 对比实验数据分析Tab.3 Comparative experiment data analysis
4 仿真实验分析
将上述改进DE 算法所求得的位姿矩阵作为机器人在对应点的动作执行方案,根据五次多项式插值求解各关节角速度、角加速度见图7—8。

图7 机器人各关节角速度Fig.7 Angular velocity of each joint of the robot

图8 机器人各关节角加速度Fig.8 Angular acceleration of each joint of the robot
各机器人各关节角速度曲线变化平滑,表明在理想条件下,机器人能够较好实现整个工作流程。各关节角加速度曲线呈现出类似正弦变化趋势,其中关节2、3 角加速度曲线关于时间轴对称。仅关节1 速度与加速度值较大,但机器人各关节先后运动,且关节1 为底部旋转关节,速度与加速度较大符合机器人快速大范围转动的特点。这说明在整个动作过程中,机器人能够稳定运行,本体未产生较大振动。
为验证前文研究所得到理想情况下关节角速度是否适合实际情况,将图7 的关节角速度作为机器人的实际工作角速度,得到机器人末端实际轨迹,见图9。

图9 机器人末端轨迹Fig.9 The trajectory of the end of the robot
机器人末端仿真轨迹对比图与机器人各关节旋转角速度对比,见图9—10。由图可知,末端执行器运动轨迹与运动学仿真运动轨迹重合,但是在运动中出现了较为明显的波动,对比关节旋转角速度曲线可知,在0.55 s~0.75 s 与3.4 s~3.6 s 时间段内实际速度在理论速度附近波动。在0.55 s 与3.4 s 角速度出现大于3.5 rad/s 的情况时,机器人末端位置产生大幅度偏差,经分析是由于角速度过大引起机器人出现波动。

图10 机器人各关节角速度对比Fig.10 Comparison of the angular velocity of each joint of the robot
因此设计以下仿真实验进行验证,增大关节5 与关节1 角速度切线斜率,降低幅值,使得各关节旋转角度总体不变、时间不变的前提下,避免机器人关节角速度出现大于3.5 rad/s 的情况。
关节角速度优化后的末端轨迹曲线与角速度变化曲线,见图11—12。由图可知,各关节角速度优化之后,机器人末端执行器轨迹的理论曲线与仿真曲线能够基本吻合,出现的偏差也在误差范围内。关节1 到6 的最大角速度均不超过3.5 rad/s,其中机器人关节角提速、降速仅需要0.01 s,其余时间内都保持匀速运动,保证机器人运动的平稳性。

图11 优化后机器人末端轨迹Fig.11 The trajectory of the end of the robot after optimization
5 结语
针对热电池组的装配要求,设计了一种装配机器人。采用改进D-H 参数法进行运动学求解,通过正运动学分析,建立机器人正解的非线性方程,计算出机器人末端轨迹。运用改进DE 算法对机器人进行求逆解,得到平均位置误差为1.4×10–4mm,平均姿态误差为2.4×10–4度,较DE 算法求解精度提高了2 个数量级。平均迭代次数为219.857,较DE 算法求解迭代次数降低了约600 次,计算效率提高了72.5%。通过动力学仿真分析确定此机器人运动过程中的振动主要与速度有关,通过优化关节角速度,将关节角速度降低至3.4 rad/s,机器人能够平稳运行,确定各构件的运动速度最大值为3.5 rad/s。通过运动学与动力学分析,以及构建机器人仿真装配模型可知,所设计的装配机器人能满足异形热电池组装配精度要求,具有较好地稳定性,为模型实际调试提供依据。
文中装配机器人的运动采用各关节依次运动的方式,较容易减小机器人本体运动产生的振动,但增加了机器人装配运动时间,并且在实际生产中机器人末端会与螺钉拧紧工具连接,因此螺钉拧紧工具的振动同样会影响装配机器人的精度。后续研究的重点可放在如何设计机器人整体运动速度以减少装配的时间,以及减小机器人末端工具的振动对机器人精度的影响。

图12 优化后各关节角速度曲线Fig.12 Angular velocity curve of each joint after optimization

