基于深度神经网络的放射性废物桶γ能谱解析方法

王江玮 顾卫国 杨 桧 王德忠

（上海交通大学机械与动力工程学院 上海 200240）

根据我国相关标准［1］，核电厂放射性废物桶在进行贮存或最终处置前需要进行测量，明确桶内所含放射性核素的种类及其活度。对废物桶进行无损测量一般选用γ能谱解析法，利用多道谱仪可以获得γ射线能谱，通过γ能谱全能峰对应的能量和计数率，可识别核素并计算其活度。

对废物桶进行γ能谱解析，关键在于桶内放射性核素种类的准确识别和活度的精确计算。传统的γ能谱解析方法首先需要对谱线进行平滑预处理，然后根据γ能谱中特征峰的峰位能量来确定放射性核素的种类，从而实现定性分析；再根据特征峰的峰面积计算出对应放射性核素的活度，从而实现定量分析［2］。我国核电厂放射性废物桶内典型的γ放射性核 素 有60Co、137Cs、54Mn、58Co、95Nb、110mAg、51Cr和125Sb等［3］。

目前多数寻峰方法均采用Mariscotti［4］提出的二阶导数寻峰法。解谱时预先建立样品核素库，在二阶导数寻峰法的基础上，将寻峰得到的峰位能量值与核素库中各核素的特征γ射线能量值进行比对，从而确定核素种类［5］。此方法简单有效，能识别弱峰，但易识别出假峰，从而造成核素误识别，例如实际解谱中发现商用解谱软件会将137Cs的661.66keV能峰识别为110mAg的657.76keV能峰。刘永刚等［6］提出了联合寻峰法，即先用一阶导数法进行全能峰峰区边界确定；然后用二阶导数法确定峰位；再用斜宽寻峰法寻峰，与二阶导数法找到的峰位对照。此方法结合了各种寻峰方法的优点，灵敏度高，但依然存在核素误识别的问题。Li等［7］提出了基于序列贝叶斯的核素快速识别方法，此方法基于环境本底辐射和目标核素辐射的事件模态序列（EventMode Sequence，EMS）建立了两个概率模型，通过后验模型的序列检测来识别目标核素。此方法能满足不同测量条件下核素快速识别的要求，但仅对137Cs和60Co两种目标核素进行了实验验证。

目前商用解谱软件对于峰面积计算普遍采用函数拟合法，且均用简单的高斯函数描述峰形［8］。通过确定峰函数的各个参数，计算峰区范围内峰函数的定积分即可求得峰面积，但此方法对于有严重拖尾的峰形计算精度较差。Siegert等［9］用高斯函数对γ谱峰进行分段拟合，并根据实际峰形修正峰函数的各个参数，此方法更好地描述了峰形，并提高了计算精度，但依然不适用于非高斯峰的峰面积计算。Qin等［10］对γ能谱信号卷积得到一种新的小波信号，提出了基于小波分析的峰面积计算方法，提高了计算精度。但此方法对γ能谱中的弱峰信号计算精度不佳。

近几年随着人工智能技术迅速发展，国内外也有学者将神经网络等机器学习方法用于γ能谱解析。神经网络是一种模仿生物神经系统结构与功能的，由多层网络节点连接组成的模型。各层节点之间有连接权重，通过对输入数据进行加权求和后，再利用激活函数处理产生输出。神经网络在各个领域都有广泛应用，对非线性模型有较好的拟合能力。Sahiner等［11］利用人工神经网络对人体肾结石的中子活化γ谱进行解析，识别了肾结石的元素组成。Samolov等［12］利用人工神经网络对不同时间段空气样本中7Be的γ谱进行解析，实现了对空气中7Be浓度的预测。核电厂废物桶内的典型γ放射性核素种类确定，理论上可以用神经网络方法进行识别。但由于废物桶内介质密度与核素分布存在差异，测得的γ能谱计数率可能相差很大；且相比于肾结石样本和空气样本，废物桶内核素种类更多，组成更复杂。目前未见报道有将神经网络方法应用于废物桶能谱解析。为了弥补传统方法在废物桶解谱上的不足，本文提出了基于深度神经网络的放射性废物桶γ能谱解析方法。

1 实验与模拟

1.1 实验

实验使用美国ORTEC公司生产的型号为DSPEC-502的数字γ射线光谱仪以及GEM系列同轴高纯锗（HPGe）探测器。谱仪的量程设定为2.9845MeV，全谱道数划分设定为16384道。探测器探头的尺寸参数如表1所示。

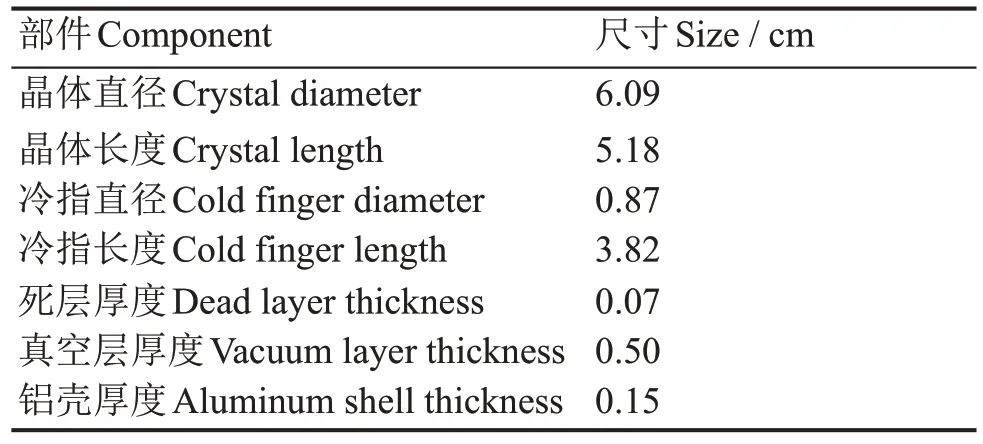
表1 探头尺寸参数Table1 Probesizeparameters

准直器外层为1cm厚的不锈钢，内层灌铅。准直口为方形，长20 cm，高9 cm。探测器探头前端距离准直口25 cm。实验使用秦山一期提供的200 L钢桶，桶高为85 cm，桶内径为56 cm，桶壁厚为0.15 cm。桶内介质分别为空气、水和沙子。秦山一期 能 提供的放 射 源仅有241Am、133Ba、137Cs、60Co和152Eu，且均为各向同性的小体源，实验操作时可视为点源。

实验前首先对实验场地测1 h的环境本底，得到本底谱的计数率。实验时把5个放射源分为单源、双源和多源的不同组合，随机放于桶内不同位置，每种组合都测10 s、30 s、60 s、100 s、300 s工况，共获得75个实验γ能谱，并根据已得的本底谱计数率对实验能谱进行环境本底扣除的处理。

1.2 蒙特卡罗模拟

根据上文ORTEC探测器、准直器和钢桶的尺寸参数，建立蒙特卡罗模型，如图1所示。

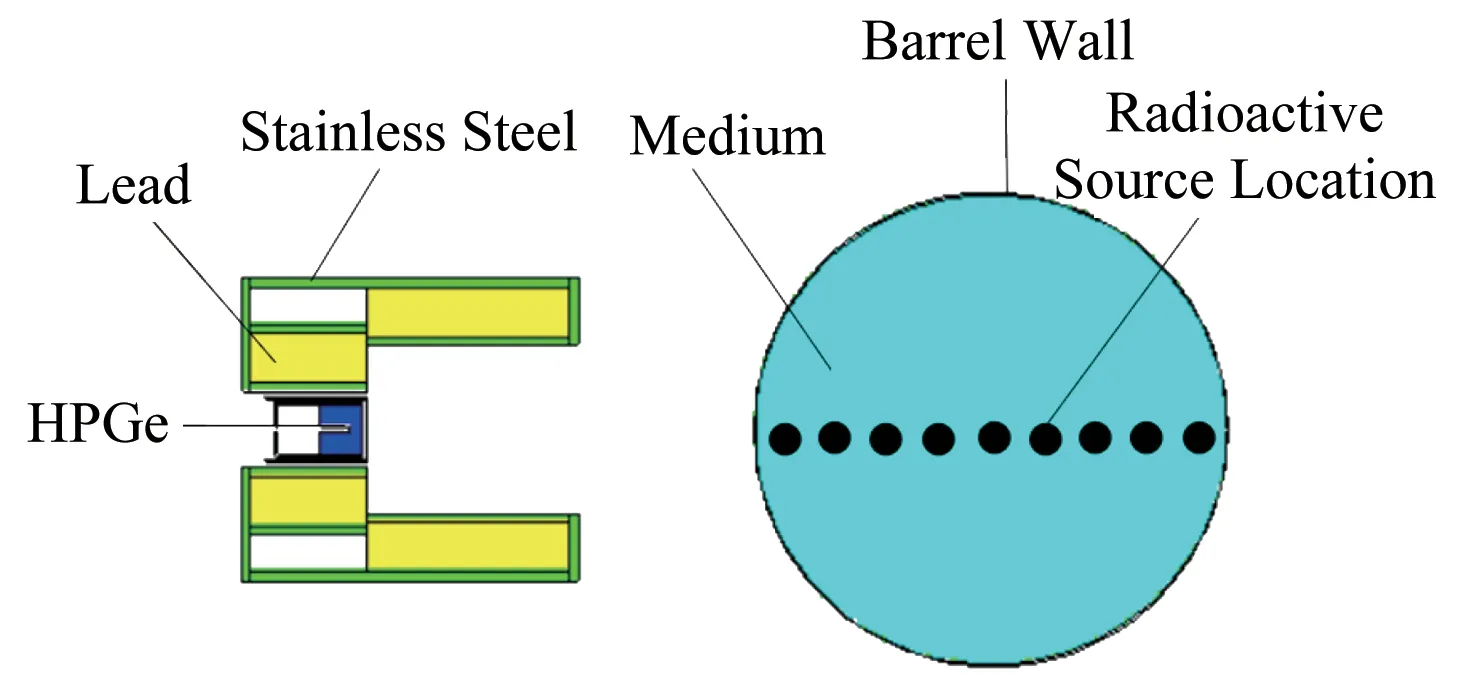
图1 测量系统蒙特卡罗模型图Fig.1 Monte Carlo model diagram of measurement system

由于存在统计涨落的影响，实验测得的γ能谱存在一定的展宽。因此利用蒙特卡罗方法模拟γ能谱时需要设定相应的展宽系数。实验使用的ORTEC探测器出厂时测定的γ射线能量与半高宽（Full Width at Half Maximum，FWHM）对应关系如表2所示。

半高宽与入射γ射线能量之间的关系可以用式（1）表示［13］：

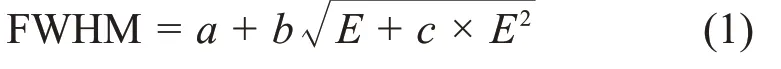
式中：a、b、c为展宽系数；E为入射γ射线能量。根据表2已知的能量及其所对应的半高宽，利用Orgin进行非线性拟合，拟合图线如图2所示。得到拟合值a为0.000 68，b为0.000 62，c为1.07，并将其用于蒙特卡罗模拟的能谱展宽中。

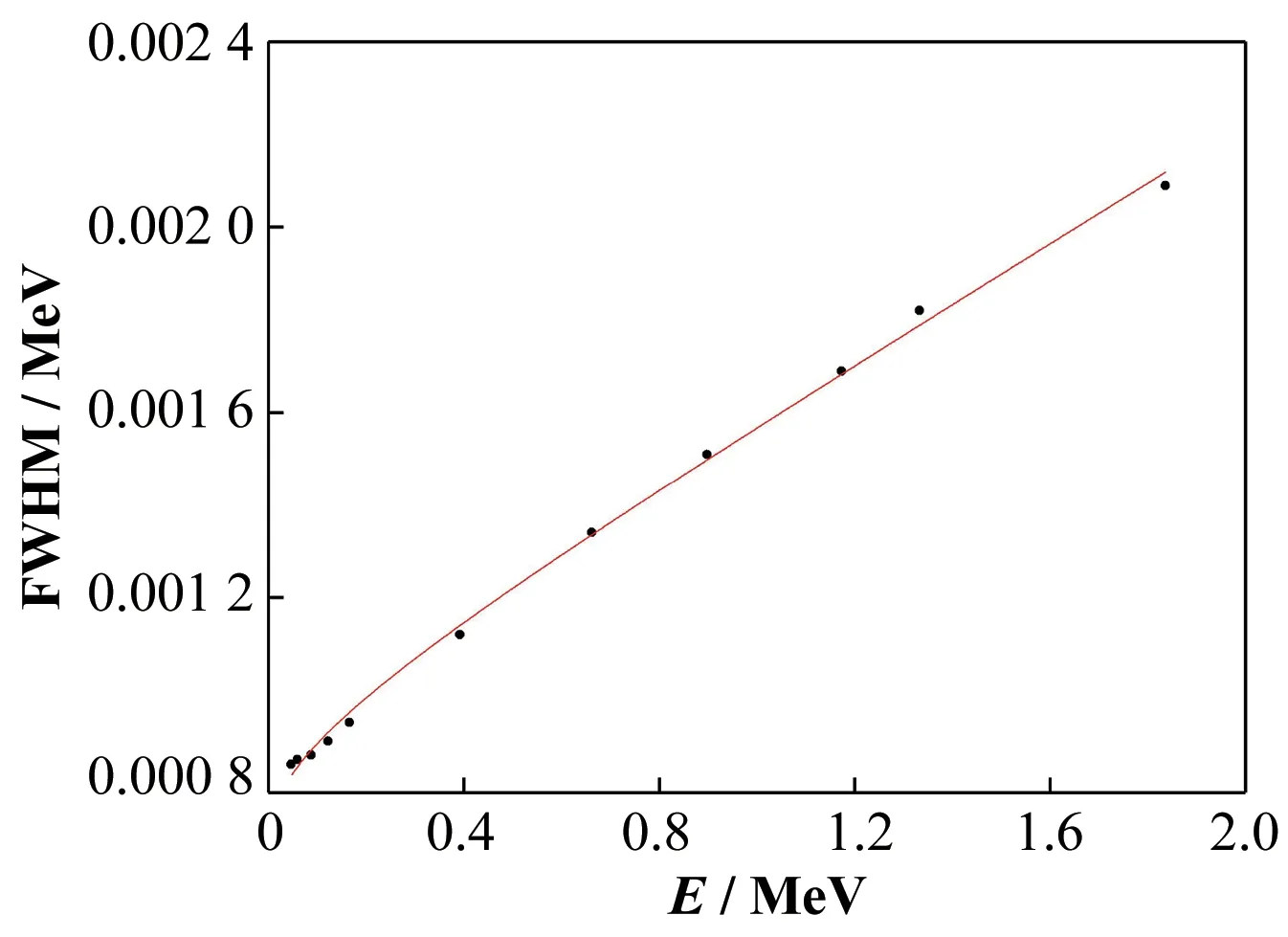
图2 能量-半高宽拟合曲线Fig.2 Energy-FWHM fitting curve

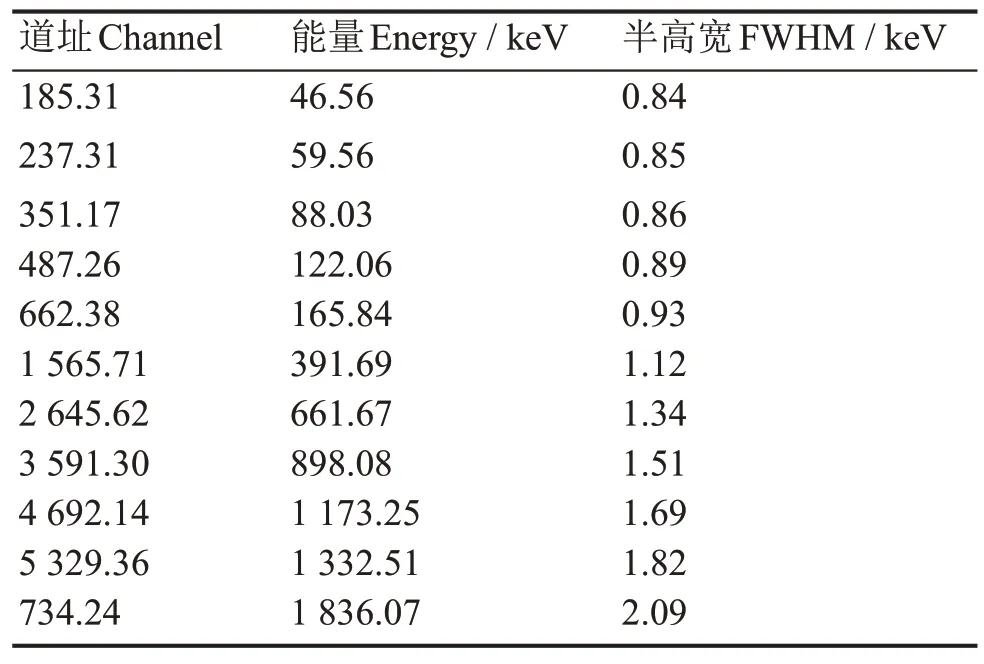
表2 γ射线能量与半高宽对应关系Table 2 Correspondence betweenγray energy andFWHM

实验测得的137Cs谱线和模拟得到的137Cs谱线如图3所示。

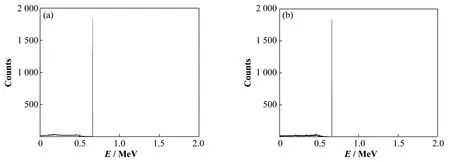
图3 137Csγ能谱曲线 (a)实验曲线,(b)模拟曲线Fig.3 137Csγenergy spectrum curve (a)Experimental curve,(b)Simulation curve

在峰值计数基本相同的情况下，实验测得的谱线峰位能量为0.661 37 MeV，半高宽为0.001 53 MeV；模拟得到的谱线峰位能量为0.661 92 MeV，半高宽为0.001 64 MeV。模拟谱线与实测谱线的相关性系数为0.94，其中使用的相关系数计算公式为式（2）：

式中：相关系数r描述模拟谱线和实验谱线的线性相关程度；x i表示模拟谱线各道址的计数；y i表示实测谱线各道址的计数；-x表示模拟谱线计数平均值；-y表示实测谱线计数平均值。r越接近于1，表示模拟谱线与实测谱线相关度越高。

由此可见，利用蒙特卡罗方法生成的模拟γ能谱与实验γ能谱基本一致，在计算中可以用模拟谱线替代实验谱线。秦山一期提供用于实验的放射源仅有5种，无法涵盖废物桶内典型γ放射性核素，故实验以外的其他核素能谱用蒙特卡罗方法模拟生成。

2 神经网络模型

2.1 神经网络解谱原理

本文使用的深度神经网络模型共有6层。输入层有1 024个节点，以全谱16 384道每道的计数作为输入数据，降维后输入到1 024个节点中。隐藏层1有512个节点，隐藏层2有256个节点，隐藏层3有128个节点，隐藏层4有64个节点，输入层和隐藏层1、隐藏层1和隐藏层2、隐藏层2和隐藏层3以及隐藏层3和隐藏层4之间都采用ReLU函数作为激活函数。隐藏层4和输出层之间采用Sigmoid函数作为激活函数。输出层有11个节点，对应11种核素，如果存在某种核素则相应的节点输出为1，不存在则输出为0。以此方法即可实现核素识别。11个节点的输出构成一个输出向量，不同核素的特征γ射线能量及其能谱对应的输出向量如表3所示。由于γ谱仪是线性时不变系统，多核素混合谱线的输出向量即为对应的单核素谱线输出向量的线性叠加［13］。

表3 核素输出向量及其主要特征γ射线能量Table 3 Output vector and main characteristicγrayenergy of nuclides

根据该ORTEC高纯锗探测器使用手册可知，全能峰峰位左右各1.5倍半高宽即为峰区左右边界［8］。由于蒙特卡罗方法模拟的能谱不存在环境本底的影响，在得到神经网络的输出向量后，即根据输出为1的核素对应的特征γ射线能量以及上文拟合得到的半高宽FWHM与射线能量E的关系式，求得特征峰的半高宽并确定峰区边界，对峰区内所有道址上的计数相加求和即为该特征峰的峰面积。

2.2 神经网络训练方法

利用神经网络进行解谱需要大量能谱数据构造数据集，而实验获取谱线费时费力，因此训练神经网络的γ能谱数据集是根据上文所述的蒙特卡罗方法模拟生成的。

根据上文所述的11种核素以及实验所用的3种不同介质，利用蒙特卡罗软件模拟生成γ能谱，包括单核素谱线及多核素混合谱线。考虑到实验里如果γ射线在介质中经过较长径迹长度的衰减，得到的谱线中可能没有低能峰；以及实验里如果测量时间过短，得到的谱线中会有弱峰。因此在模拟谱线时放射源设置在相对于桶中心在-20~20 cm，一共9个与探测器晶体在同一轴线但距离不同的位置上，如图1所示；模拟谱线的发射粒子数设置为六次方、七次方和八次方三个不同数量级。去掉计数为0没有谱线的情况，一共模拟生成了2 139个γ能谱，随机选取其中2 000个γ能谱作为数据集用于神经网络训练。

本文使用的神经网络模型在训练中使用的损失函数是交叉熵函数。使用的优化函数是Adam函数，学习率设置为0.001。训练过程中把数据集按照七比三的比例随机分为训练集和测试集两部分。模型训练的迭代次数设为500次。

3 结果分析

训练得到的神经网络能够快速收敛，核素识别准确率达到96.47%。核素识别准确率定义为测试集能谱在神经网络中的输出向量和其真实输出向量一致的比例。准确率随迭代次数变化曲线如图4所示。

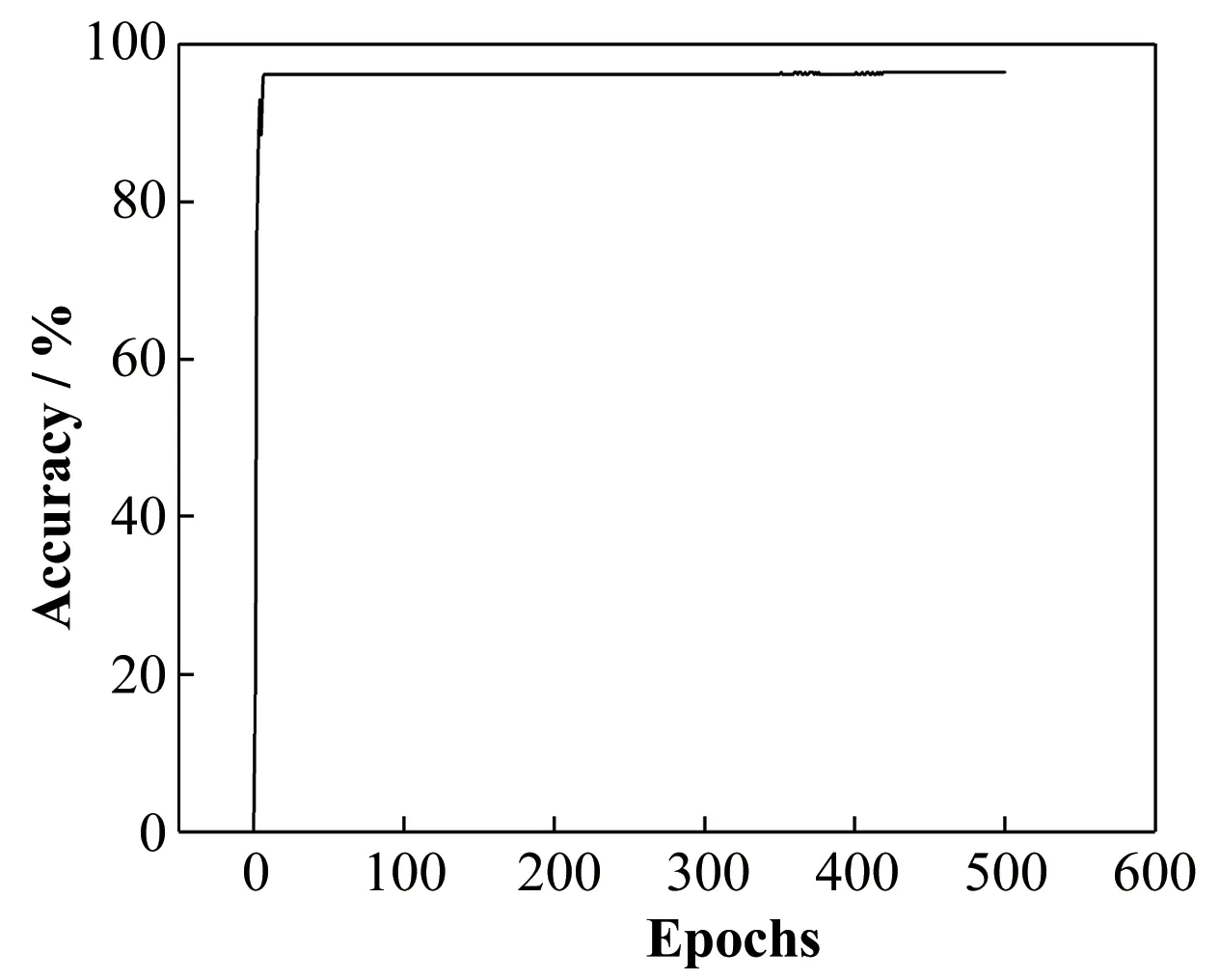
图4 预测准确率随迭代次数变化Fig.4 Prediction accuracy-epochs curve

选取部分实验能谱和部分未经训练的模拟能谱作为验证集，输入到训练好的神经网络进行验证。其 中241Am、60Co、137Cs、241Am+137Cs、60Co+137Cs和241Am+60Co+137Cs 6种不同核素组合的能谱是实验能谱；137Cs+110mAg、95Nb+110mAg和54Mn+95Nb+51Cr三种不同核素组合的能谱是模拟能谱。核素识别结果如表4所示，峰面积计算结果如表5所示。表5中真实峰面积是打开谱线文件将全能峰附近道址的计数手动相加求和得到的，传统方法峰面积计算采用高斯函数拟合法。

表4 核素识别结果Table 4 Results of nuclide identification

由表5可得，神经网络方法和传统方法的峰面积计算误差都与峰面积本身大小相关。为了进一步确认误差与峰面积的关系，选取了不同强度的137Cs实验能谱，分别用神经网络方法和传统方法计算峰面积并比较误差。结果如表6所示。

由表4可得，训练后的神经网络模型预测的输出向量和真实输出向量之间误差很小，不会产生核素误识别。由表6可得，由于传统方法的峰面积计算采用高斯函数拟合法，当谱线计数较低，峰面积较小时，峰形偏离高斯分布，计算误差较大；当谱线计数较高，峰面积较大时，峰形接近高斯分布，计算误差较小。神经网络方法识别核素后根据半高宽确定峰区边界，将峰区内所有计数相加即为峰面积。因此误差来源仅是真实峰的峰区边界与根据半高宽确定的峰区边界之间相差的道址计数，对于不同强度的137Cs实验能谱，峰面积计算误差基本在1%左右，对于弱峰的峰面积计算误差也控制在10%以内。由表5可得，对于不同核素的能谱，基于神经网络核素识别后计算的特征峰峰面积，计算精度均高于传统方法。尤其对于弱峰的峰面积计算，相比传统方法计算精度有很大提高。

表5 峰面积计算结果Table 5 Results of peak area calculation

表6 不同强度137Cs能谱峰面积计算结果Table 6 Peak area calculation results of different intensity 137Cs energy spectrum

4 结语

本文利用深度神经网络进行γ能谱解析，模型的预测准确率达96.47%。且解决了传统解谱方法存在的核素误识别和峰面积计算精度不佳的问题，并用实验γ谱线验证了神经网络方法的有效性。神经网络只对经过训练的核素产生正确的输出，因此用于训练的核素要包含所有用于验证的核素。若要识别更多的核素，则需要修改数据集加入新核素的信息重新训练模型。由于实验中获取大量核素能谱数据费时费力，故可以用蒙特卡罗方法模拟所得的能谱数据进行训练。

作者贡献声明王江玮：直接参与论文研究，负责实验与模拟，负责神经网络模型搭建并撰写论文；顾卫国：指导实验操作和论文修改；杨桧：提供技术支持；王德忠：提供技术支持。