分子筛中碳氢化合物扩散行为的分子模拟研究进展

杨 光，杜钰珏，柯 俊，胡文德，王仰东，王传明，谢在库

绿色化工与工业催化国家重点实验室，中国石油化工股份有限公司上海石油化工研究院，上海 201208

作为一类重要的无机固体材料，分子筛被广泛用于催化、吸附和分离等领域[1]。分子筛由于其规整的孔道结构、独特的择形性能以及适宜的酸性，在石油化工和固体酸多相催化等方面有着极为重要的应用，例如催化裂化、甲苯歧化、甲醇制烯烃（MTO）、丙烯环氧化、生物质转化、NOx选择性还原和合成气一步催化转化等[2-4]。大量研究指出，催化反应中各物质（反应物、中间体和产物）在分子筛孔道内的扩散是影响反应选择性和产物分布等催化性能的重要因素之一，因此分子在限域条件下的扩散行为和动力学研究引起了学术界和工业界的大量关注。

扩散是极其复杂的动态过程，整个扩散受到温度、客体分子结构和负载量、主体多孔材料拓扑结构和组成等多个因素的影响，给实验研究带来诸多挑战。近年来随着高性能计算技术以及模拟计算方法和程序的发展，计算机模拟已成为研究分子筛中客体分子扩散动力学的重要手段。模拟研究可以在分子水平上理解扩散机制，能够深入考察分子筛孔道中客体分子的扩散细节，并且通过使用特定的理论模型，能够对影响扩散的各个因素单独地进行评价，最终实现分子筛扩散动力学的深入研究。

用来研究客体分子在分子筛中扩散行为的理论及模拟研究方法包括分子动力学（Molecular Dynamics，MD)、过渡态理论（Transition State Theory，TST）、过渡路径采样（Transition Path Sampling，TPS）以及动力学蒙特卡罗（Kinetic Monte Carlo，KMC）等[1,5-10]。在分子筛扩散研究领域，多年来基于力场的各种分子动力学模拟最为广泛，系统研究了温度、分子筛拓扑结构和酸性、客体分子结构和负载量等与扩散性能之间的关系。

本文主要关注分子筛扩散的分子动力学模拟，对研究方法、分子筛中单组分碳氢化合物（烷烃、烯烃和芳烃）扩散以及多组分扩散进行综述。

1 分子筛扩散研究方法

扩散的理论研究通常是采用基于经典力场的分子动力学模拟来处理温度、客体分子的运动以及主体骨架结构的刚柔性等因素的影响。分子动力学的基本思想是要跟踪客体分子随着时间运动的轨迹，再通过统计平均获得扩散的平衡性质和运动特性，进而通过各种理论方法获得各种扩散动力学数据。下面将从扩散动力学、分子力场以及“慢”扩散方面对模拟方法进行表述。

1.1 扩散动力学

扩散系数是描述传质过程和扩散性能的一个参数，通常可以分为传递扩散系数（transport diffusion coefficient）、互扩散系数（collective diffusion coefficient）和自扩散系数（self-diffusion coefficient）[11]。传递扩散系数主要通过宏观吸附实验测量，互扩散系数和自扩散系数可以通过分子模拟方法计算得到。互扩散系数将传递扩散中的浓度梯度转换为化学势梯度，其中研究比较广泛的是Maxwell-Stefan（M-S）扩散系数，通过跟踪客体分子扩散的速度自相关函数获得。在多组分混合物中，可以将其中一个组分的速度与所有其它组分（包括该组分）相关联，因此M-S扩散系数适用于多组分混合物扩散的研究[12-13]。本文重点关注分子模拟易于计算的自扩散系数。自扩散系数是标记客体分子在给定时间间隔内产生的均方位移（Mean Square Displacement，MSD）的参数。自扩散系数不考虑浓度梯度的影响，通常在相同条件下低于互扩散系数[14]。在零负载的极限条件下，传递扩散系数、互扩散系数和自扩散系数趋于一致[15]。在脉冲场梯度核磁共振（PFG-NMR）实验中，标记分子的信号衰减与自扩散系数直接相关[11]。Bu等[16]利用MD方法模拟计算了代表生物质热解蒸汽的几种选定分子的扩散系数，发现ZSM-5分子筛中的水、甲醇、乙醇醛和甲苯的自扩散系数与室温下核磁共振（NMR）的表征结果一致[17]。Gao等[18]利用PFG-NMR技术和MD方法计算了甲烷、乙烷和丙烷等烷烃在8元环分子筛（LEV，CHA和RHO）中的自扩散系数，获得的实验结果和模拟结果相近，且扩散系数在3种结构分子筛中的变化规律一致（见图1和图2）。

图1 载量为每笼2个分子的甲烷在分子筛中的自扩散系数[18]Fig.1 Self-diffusion coefficients of methane with 2 molecules per cavity in zeolites [18]

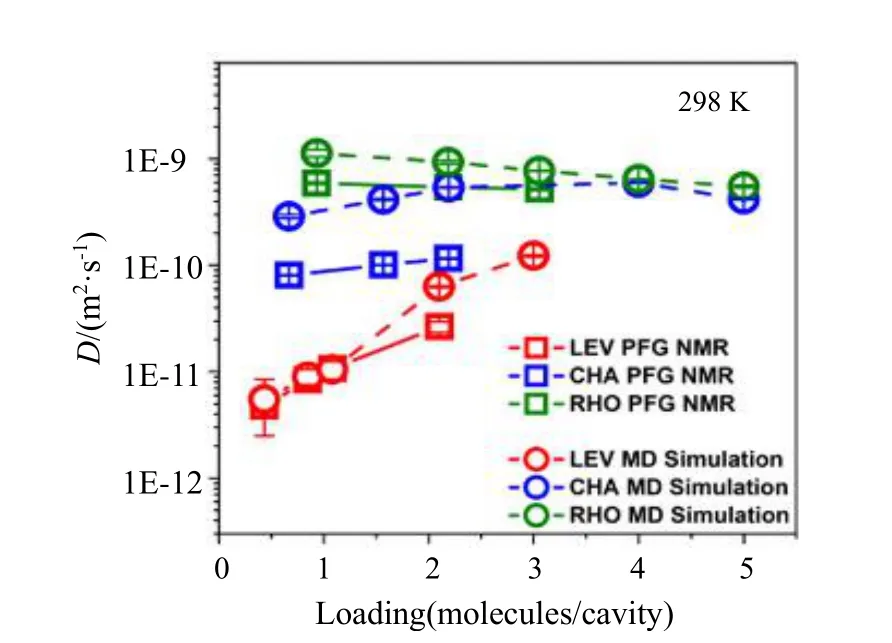
图2 甲烷在笼型分子筛中自扩散系数对负载量的依赖性[18]Fig.2 The dependence of self-diffusion coefficients on loading for methane in cavity-type zeolites [18]

通常，长时间极限下MSD的斜率看作是自扩散系数的倍数。一个客体分子在时间间隔内的MSD是由分子行进的距离来度量的。按照爱因斯坦关系式，将MSD在一定时间区间内进行线性拟合（最小平方拟合），即得到自扩散系数（Ds）：

式中：MSD为均方位移，Å2；τ为时间间隔，s；Ds为自扩散系数，m2/s。在一维方向上扩散时，a=2；在二维平面上扩散时，a=4；在三维空间中扩散时，a=6。b是均方位移在零时刻的偏移，Å2。该公式被广泛用于研究不同分子筛上的各种烃类分子的扩散[11,19-26]。

值得注意的是，由于分子筛结构的非均匀性和各向异性，还会出现反常扩散现象，即客体分子的均方位移与扩散系数、时间之间不再满足爱因斯坦关系，而是表现出反常的幂律趋势：

式中：Dα是反常扩散系数，m2/s；α是反常扩散指数。目前反常扩散现象与分子筛结构关系的研究较少，反常扩散系数和反常扩散指数的确定具有巨大的挑战性，在本文中不展开讨论。

实验表明，客体分子在分子筛孔道中的自扩散遵循阿伦尼乌斯（Arrhenius）方程：

式中：D0为扩散指前因子，m2/s；Ea为自扩散活化能，kJ/mol；R为气体常数，8.314 J/(mol·K)；T为温度，K。通过模拟计算得到不同温度下的自扩散系数，按式（3）将Ds对温度进行拟合可以估算出自扩散活化能和自扩散指前因子。

客体分子通过相邻笼子之间的窗口进行扩散被认为是一个受阻过程，也就是说一个分子跳跃的速率取决于该分子通过窗口需要克服的自由能垒。通过特定窗口的自由能垒（ΔF）可由如下公式计算获得：

式中：P表示分子通过窗口的概率；kB是玻尔兹曼常数，1.380 6×10-23J/K。

此外，非键相互作用能也是影响客体分子在不同结构分子筛中扩散的重要因素。通常采用固定扩散路径的方法，将客体分子在分子筛孔道中沿着预先定义的扩散路径，按照设定的等距步长从一个晶格移动到相邻晶格，在每个位置上计算分子筛骨架和客体分子之间的相互作用能，通过计算沿扩散路径的最低和最高局部能量之间的差异可以确定跨越孔口和孔道的能垒。一般来说，扩散活化能、扩散自由能和非键相互作用能与分子筛结构有很强的相关性，这些参数为考察分子筛的择形性、扩散性能与客体分子尺寸和分子筛孔道结构之间的关系等提供理论基础[18,27]。

1.2 分子力场

分子动力学等分子模拟技术需要准确的力场来描述客体分子与主体分子筛骨架之间以及客体分子之间的相互作用。然而，为特定分子筛体系选择准确的力场并不容易，而且一般来说，为分子筛开发的力场迁移性较差[28]。大量的力场被应用于纯硅分子筛、铝硅分子筛和铝磷硅分子筛的MD模拟，并得到了较好的结果[5,27-32]。在众多力场中，Hill-Sauer力场[33-34]应用较为广泛。Awati等[19]采用Hill-Sauer力场系统建立了LTA，CHA，ERI和BIK 4种具有不同窗口尺寸的8元环分子筛的柔性模型，研究了不同分子筛结构对甲烷扩散性能的影响。Bu等[16]研究二甲苯异构体在ZSM-5中的扩散性质，采用了Hill-Sauer力场描述分子筛骨架，得到的模拟结果与实验结果符合得较好。Boulfelfel等[9]对Hill-Sauer力场中与Si—O—Si和O—Si—O有关的参数进行修改，提高了描述小孔分子筛中孔径和骨架柔性的准确性。此外，经典的COMPASS、CVFF力场已被证明能够准确地预测小分子在不同分子筛材料中的扩散和吸附。Wang等[7]采用COMPASS力场进行MD计算，深入研究了具有8元环、10元环和12元环孔道的CHA，MFI，BEA和FAU分子筛中乙烯和丙烯的扩散动力学。Liu等[35]采用CVFF力场进行MTO反应中的代表性物种（甲醇、多甲基苯和烯烃）在一维ZSM-12和ZSM-22分子筛中扩散的MD模拟。近年来，发现核壳力场[36-37]的MD模拟虽然对计算时间的要求较高，但核壳力场已被证明是再现分子筛结构特性的更为准确的方法。但在很多情况中，现有力场还无法准确描述实际工业中的复杂分子筛体系，如多孔纳米材料中的扩散，因此通过基于第一性原理的密度泛函理论（Density Functional Theory，DFT）构建衍生力场用于MD模拟，可提高力场的准确性和可靠性[1,38-39]。

1.3 “慢”扩散和稀有事件

通过经典的分子动力学方法可以较好地模拟一些低碳烷烃、烯烃的扩散，并定量计算出自扩散系数，但是当客体分子在分子筛内的扩散非常慢，常规的动力学方法就难以适用。例如，传统MD方法对乙烯这种小分子扩散可以在有限的模拟时间内得到较好的结果，然而对于丙烯则较难跟踪其在LTA和CHA等小孔分子筛中的扩散[9,40]，使得分子运动的MSD与扩散时间不能呈现良好的线性关系[7]，这是因为在模拟过程中需要克服的扩散能垒过高，短时间内不能通过MD有效及准确地产生分子的运动轨迹[11,41]。在这种情况下，需要采用其它技术来研究扩散，包括TST，TPS或KMC等，其中TST是用来研究分子筛中“慢”扩散问题较为广泛的方法，采用这种方法可以在MD无法达到的时间尺度上预测客体分子的扩散行为。TST方法将扩散行为看作是分子从一个晶格到另一个晶格的跳跃过程，跳跃过程本身的高能垒使其成为一个稀有事件，且前后跳跃过程不相关。通过基于反应坐标的自由能计算得到跳跃频率，再由跳跃频率获得扩散系数。近年来TST在传统方法上有了发展，例如在纳米多孔材料中，改进了原有的刚性分子筛骨架，将TST应用于柔性骨架中，考察了客体分子尺寸与分子筛孔径大小之间的关系对扩散性能的影响[42-44]。

在最近的报道中，Cnudde等[40]结合第一性原理和高级采样技术在分子尺度上研究了低碳烯烃在SAPO-34分子筛中的扩散，其中乙烯和丙烯通过8元环分子筛窗口的扩散自由能使用从头算分子动力学方法来确定，该方法被称为从头算伞形取样（Ab Initio Umbrella Sampling，AIUS），它为解决分子筛限域下的“慢”扩散问题提供了新思路。

2 单组分扩散

研究单一结构客体分子在分子筛中的扩散是研究复杂扩散过程的基础，单组分扩散的研究对揭示温度、客体分子的负载量（简称负载量）、分子筛结构、酸性位等因素的影响具有重要意义，同时也是测试验证模拟计算方法可靠性的重要手段。目前已有大量工作对水、烃类分子、醇等单组分客体分子在分子筛孔道中的扩散进行了模拟研究，本文主要总结烷烃、烯烃和芳烃等烃类化合物在分子筛中扩散的分子模拟研究结果。

2.1 烷烃扩散

2.1.1 甲烷

从计算的角度来看，甲烷分子相对较小，扩散系数足够高，利用经典的分子动力学模拟可以较为透彻地探讨其扩散行为的影响因素，因此甲烷在各类分子筛中的扩散研究受到广泛关注。

首先，温度是影响客体分子扩散行为的重要因素。在分子扩散运动中，温度的升高加剧了分子的热运动，使分子的扩散速率增加。如果分子跳跃所要克服的自由能垒与温度无关，则扩散系数与温度的变化趋势符合Arrhenius行为。甲烷在很多分子筛体系中的扩散符合这一行为，例如采用MD和TST方法观察到高温和低温下甲烷在8元环分子筛LTA，CHA，ERI和BIK中的扩散行为[19]，以及甲烷在中孔分子筛MFI，MEL，PON，BOF，PSI和ATO中的扩散行为[45]。López等[46]采用MD方法研究负载量较小时甲烷在MFI分子筛中的分布和扩散，发现在高于250 K时呈Arrhenius行为而低于该温度时出现偏差（见图3），并通过能量及自由能变化解释了该Non-Arrhenius行为是熵效应引起的，即甲烷在低温时倾向于吸附在中心孔道位置，而高温下优先吸附在交叉孔道位置，吸附位置的不同导致甲烷在低温和高温下扩散所克服的能垒不同，从而出现了Non-Arrhenius现象。

图3 甲烷在MFI分子筛中扩散时的Non-Arrhenius行为[46]Fig.3 Non-Arrhenius behavior of methane diffusion in MFI zeolite below 250 K[46]

其次，负载量对客体分子在分子筛中的扩散性能有重要影响。前面提到，在无限稀释的极限情况下，自扩散系数与互扩散系数严格等效，这被称为Darken近似，即假设修正后的扩散系数与负载量无关。Skoulidas等[47-48]使用MD方法系统研究了各种分子筛中甲烷的扩散系数，表明Darken假设对于大多数分子筛不成立，甲烷在ITQ-3，ITQ-7和ZSM-12分子筛中的扩散系数随负载量的增加而下降，在MFI分子筛中先增大后急剧下降。Krishna等[49]采用KMC和MD方法研究发现，甲烷在LTA分子筛中的扩散系数随负载量增加先增大后降低，而在FAU分子筛中扩散系数随负载量增加线性下降。Beerdsen等[50-51]采用动态校正过渡态理论方法（dynamically corrected Transition State Theory，dcTST）和MD方法计算了非零负载下分子的扩散行为，发现甲烷在笼型LTA分子筛中的扩散系数随负载量的变化关系极为复杂：先增加到最大值后逐渐降低，再增加到出现第二个较小的极值峰再降低。根据自由能曲线可以得出这一现象是由分子-笼壁相互作用力和分子-分子相互作用力的竞争导致：随着负载量的增加，笼内分子间相互作用力逐渐增强，取代了原来有利的分子-笼壁相互吸引力，导致谷底（笼中心）自由能增加，而窗口区的自由能几乎没有变化，因此绝对自由能垒降低，扩散系数增加，直至出现最大值（每个笼子中大约有10个分子）；随着分子筛慢慢被填满，笼子内的分子变得越来越有序，新的分子间相互作用力占主导，扩散减慢；当每个优选位置都被占据（每个笼子中约有15个分子）时，甲烷分子在笼子内遵循高度有序的模式，再添加另一个分子意味着必须打破这种有序结构，形成新的排序，这种新的排序改变了自由能曲线的形状，扩散系数再次增加；随着新排序中的位置再次被分子填满，扩散系数到达第2个小峰值后再次减少。由于高负载量下的扩散系数第2个小峰值的出现需要非常高的压力，因此很难通过实验观察到。

研究发现甲烷的扩散系数随负载量的变化与分子筛结构密切相关。Beerdsen等[14,52]采用分子模拟研究了甲烷在各种分子筛结构中的自扩散系数和互扩散系数的负载依赖性，并根据计算结果和自由能垒上的跳跃率将甲烷的扩散行为按照分子筛结构进行分类：三维笼状分子筛（SAS，CHA，ERI和LTA）中随负载量的增加先增加后降低；一维孔道分子筛（MTW，LTL和AFI）中随负载量的增加快速降低；三维交叉孔道分子筛（ISV，BOG和MFI）中随负载量增加下降趋势逐渐变缓。并结合甲烷在3种结构分子筛中的自由能随孔道坐标的变化进行了解释，如图4和图5所示。由图可知，笼状分子筛随着负载量的增加，笼中心自由能增加，而窗口区的自由能几乎不变，因此自由能垒降低，扩散系数增加。随着负载量的继续增加，窗口区的自由能增加，导致自由能垒升高，扩散系数降低。一维孔道分子筛的自由能垒随负载量（低负载区）的增加而明显增大，扩散快速减慢。三维交叉孔道分子筛的自由能垒也随负载量的增加而增大，但增大程度较一维孔道分子筛较小。

图4 300 K下甲烷的自由能曲线随负载量的变化[52]Fig.4 Free-energy profiles of methane as a function of loading at 300 K [52]

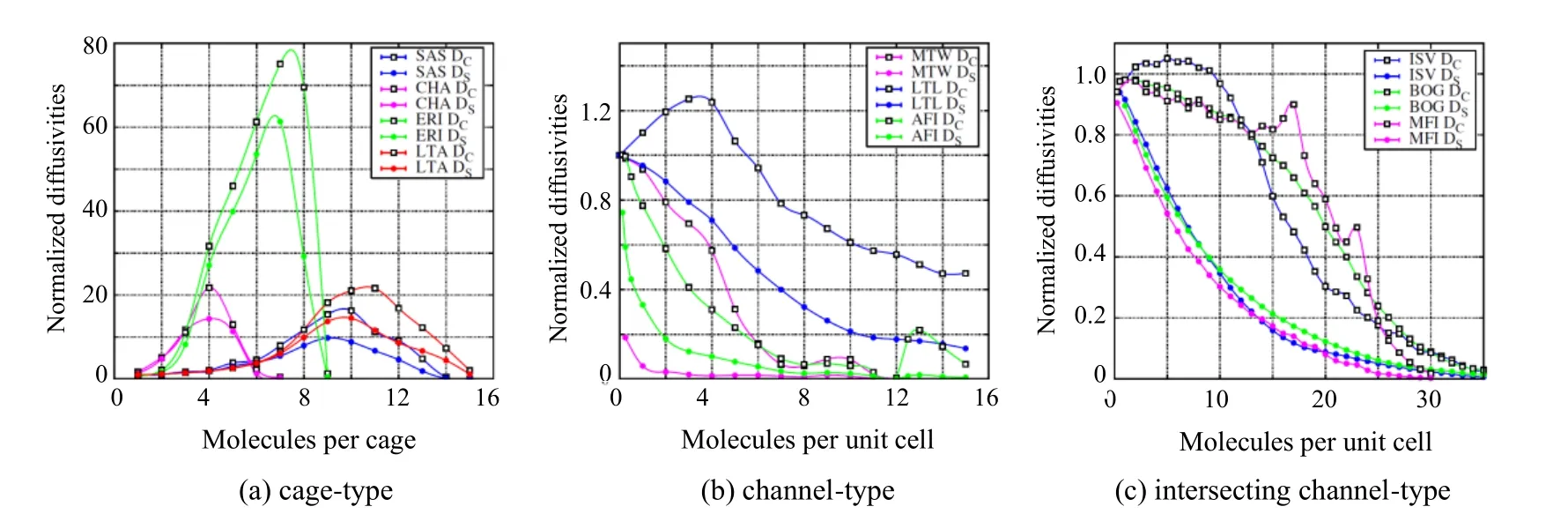
图5 300 K下甲烷的归一化扩散系数DS和DC随负载量的变化[52]Fig.5 Normalized diffusion coefficient DS and DC of methane as a function of loading at 300 K [52]

Krishna等[53]研究甲烷在交叉孔道（MFI，ISV和BEA)、一维孔道（AFI，TON，FER，MOR和LTL）和笼型结构（FAU，LTA，ERI，CHA和DDR）中的扩散也得到类似的结论。Krishna[54]还采用MD方法计算了分子筛、金属有机骨架（MOFs）、共价有机骨架（COFs）、碳纳米管（CNTs）和具有各种孔隙拓扑结构的圆柱形二氧化硅中甲烷及其混合物的M-S扩散系数，并通过自由能计算进行解释：在孔径为2～50 nm的介孔材料中，客体分子与孔壁相互作用对扩散的影响很小，可以忽略不计；在中孔材料中，扩散受分子-分子和分子-孔壁相互作用竞争的影响；在孔径小于2 nm的微孔内，孔壁表面力场对客体分子的影响占主导。Gao等[18]通过MD模拟和PFG-NMR实验表明，负载量对自扩散系数的影响程度是由分子筛孔径的大小决定的，在8元环分子筛LEV，CHA和RHO中，分子筛孔道越小，自扩散系数随负载量的变化越快。Liu等[45]采用MD方法和蒙特卡罗（Monte Carlo，MC）方法相结合，系统研究了短链烷烃在一维直链（PSI和ATO）、一维弯曲（PON和BOF）和三维交叉（MFI和MEL）孔道分子筛中的扩散行为，发现在一维弯曲孔道中烷烃的扩散比在直孔道中的慢；在三维交叉孔道中，自扩散系数是各向异性的并且强烈依赖于每个互连的一维直孔道，且弯曲孔道中自扩散系数对温度更敏感。

此外，分子筛拓扑结构和骨架的刚柔性也是分子动力学研究分子扩散的一个重要方向。Krishna等[20]采用MD方法研究了甲烷及其混合物在8元环DDR，CHA，LTA，ITQ-29和TSC分子筛中的扩散性能，发现甲烷自扩散系数的大小与窗口开口的大小直接相关，窗口孔径每增加0.5 Å，自扩散系数就会增加大约2个数量级。Krishna等[55]研究发现分子筛刚性和柔性骨架对甲烷在CHA和LTA等分子筛中的扩散系数影响较小。而García-Sánchez等[21]则认为在LTA型分子筛中，骨架柔性对甲烷的自扩散影响很大，且影响程度取决于所使用的模型。Awati等[19]系统地表征了骨架柔性对4种具有不同窗口直径的分子筛LTA，CHA，ERI和BIK中甲烷扩散行为的影响，表明对于动力学直径与窗口大小相当（或大于）的分子，完全柔性骨架与刚性骨架的模拟结果可以产生数量级的扩散差异，同时Awati等[19]结合了经典分子动力学和过渡态理论，快速准确地预测了甲烷的扩散系数，与使用完全柔性骨架的MD模拟结果一致，并将这两种新方法应用于多孔有机笼状晶体（POCs）[42]和MOFs[43]中的分子扩散研究中。

2.1.2 乙烷、丙烷和直链烷烃

同甲烷一样，乙烷、丙烷这类小分子能在CHA，AFX和AEI等拓扑结构的小孔分子筛中扩散[6,8]。而对于长链烃类化合物，如丁烷、戊烷、己烷、庚烷、辛烷以及更长的烃类，需要在更大孔径的分子筛中才能表现出良好的分子扩散性能，显示出分子模拟结果与实验数据的合理性和一致性[11]。在经典分子动力学中，为简化计算，通常将烷烃分子以联合原子的形式进行建模，将其中的CH4，CH3和CH2视为单个相互作用单元[44,56-58]。

温度和客体分子的负载量仍然是影响直链烷烃扩散行为的重要因素。Beerdsen等[50-51]采用dcTST方法计算非零负载下乙烷和丙烷在LTA分子筛中的扩散系数，得到与前面甲烷类似的结果，即扩散系数随负载量增加先增加到最大值再逐渐降低。Hussain等[56]采用MD方法研究发现，在300 K和400 K下甲烷、乙烷和丙烷在MFI分子筛中的自扩散系数随温度的升高而增加，随负载量的增加而降低，随客体分子原子数的增加而降低，即甲烷＞乙烷＞丙烷。300 K下，正丁烷在MFI分子筛中扩散系数也随负载量增加而降低[57]。分子间相互作用力随着原子数增加逐渐增强，因此在大多数分子筛中遵循自扩散系数随客体分子原子数的增加而降低的规律。然而共振扩散效应会导致相反的规律出现。Schuring等[59]在采用MD方法研究正烷烃在沸石丝光沸石、镁碱沸石和ZSM-22分子筛中扩散时发现只要扩散分子的长度是主晶格周期的整数倍，就会发生共振扩散效应。Liu等[45]指出在一维弯曲结构BOF分子筛中，丙烷的自扩散系数要大于甲烷和乙烷，这是由于共振扩散导致的。正如前面所述，在较高温度下分子通常扩散得更快，然而Yuan等[58]通过实验和MD模拟观察到在MFI和TON分子筛的限制下，长链分子正十二烷烃的自扩散系数随温度的升高而降低，这种异常扩散是由于长链分子在高温下发生弯曲，产生“热阻效应”而引起的，且在高温下发生弯曲的直链分子的扩散阻力与支链结构分子的扩散阻力相当。在较大孔分子筛AFI和VFI中则不存在“热阻效应”。

刚性、柔性分子筛骨架的理论应用对长直链烷烃的扩散研究尤为重要。Leroy等[57]采用了平衡分子动力学（Equilibrium Molecular Dynamics，EMD）方法研究刚性和柔性骨架对吸附在MFI分子筛中一系列正构烷烃自扩散系数的影响，表明骨架刚柔性对客体分子扩散行为的影响取决于客体分子的长度和负载量：在较短的烷烃（甲烷和正丁烷）和低负载量的情况下，由于客体分子-分子筛势能面的微弱改性导致分子在柔性骨架中的扩散得到增强；在高负载量及长链烷烃（正己烷和正辛烷）下，扩散行为主要由客体分子之间的相互作用控制，柔性骨架对分子自扩散系数的影响不大。该研究还指出，无论在刚性还是柔性骨架模拟中，从甲烷到正己烷的自扩散系数随着烷烃链长的增加平滑降低，对于较长的烷烃（C7以上），该力场下的MD结果则不能再现实验观察到的扩散系数急剧下降的情况。Combariza等[60]分别采用基于BKS力场和PMM力场的MD方法研究了温度对8元环分子筛CHA和SAS中丙烷扩散性能的影响，发现PMM力场预测所选结构分子筛的窗口尺寸更宽，自扩散系数稍大；2种力场下窗口尺寸在较高温度下显著加宽，从而得到较低的扩散活化能；BKS力场描述的窗口尺寸随温度的升高加宽更多，自扩散系数增大明显，得到的活化能比PMM力场低。Sastre[8]进一步计算表明，丙烷在8元环分子筛AFX和AEI中的扩散是一个活化过程。Boulfelfel等[9]采用MD和TPS方法，克服室温下缓慢扩散过程引起的时间尺度问题，计算了C1～C4直链烷烃在LTA分子筛中的扩散系数，表明骨架柔性对丙烷和丁烷扩散行为的影响远大于甲烷和乙烷。此后又首次采用dcTST方法计算了全柔性骨架的金属有机骨架化合物（ZIF-8）中乙烷、丙烷等分子的扩散系数，结果与实验数据相一致[44]。

2.1.3 支链烷烃

由于空间位阻效应，支链烷烃在分子筛孔道中的扩散比直链烷烃更受限制。Smit等[61]通过MC方法分析了直链和支链烷烃在直线-锯齿形（zig-zag）交叉孔道分子筛中的吸附位置和自由能曲线，发现直链烷烃在所有孔道中可以相对自由移动，而支链烷烃大多数时候被困在分子筛的zig-zag孔道和直孔道的交叉处，偶尔会从一个交叉点跳到另一个交叉点，由跳跃率计算出的扩散系数与实验数据具有一致性和合理性。Schuring等[59]采用MD方法研究发现支链烷烃在丝光沸石、ZSM-5、镁碱沸石和ZSM-22分子筛中的自扩散行为也强烈依赖于负载量，并且异丁烷和2-甲基戊烷在丝光沸石分子筛中的自扩散系数比同分子量的线性烷烃慢不到1个数量级，而在ZSM-5和ZSM-22分子筛中，由于体积大的支链烷烃与孔道紧密结合，与线性烷烃自扩散系数差高达3个数量级。Van Baten等[62]采用构型偏倚蒙特卡罗（Configurational Bias Monte Carlo，CBMC）模拟和MD方法研究了己烷异构体和丁烷异构体在MOR，FAU和MFI分子筛中的吸附和扩散，结果见图6。发现分子筛的拓扑结构对直链和支链烷烃的扩散有重要影响：在一维MOR分子筛中，更紧凑的支链异构体具有更小的有效分子长度，在孔道内具有更高的填充效率，因此在低负载量下，细长的直链异构体比更紧凑的支链异构体扩散得更快；而在高负载量下，填充熵效应会导致扩散系数发生逆转，即2,2-二甲基丁烷（22DMB）比正己烷（nC6）扩散得快，异丁烷（iC4）比正丁烷（nC4）扩散得快。对于笼型FAU分子筛，发现直链和支链异构体具有几乎相同的吸附强度，因此扩散系数也彼此接近。对于交叉型MFI分子筛，熵效应的作用方式与MOR分子筛相反，支化的2-甲基戊烷（2MP）更喜欢位于交叉点处，与直链正己烷相比，其扩散系数可以忽略不计。

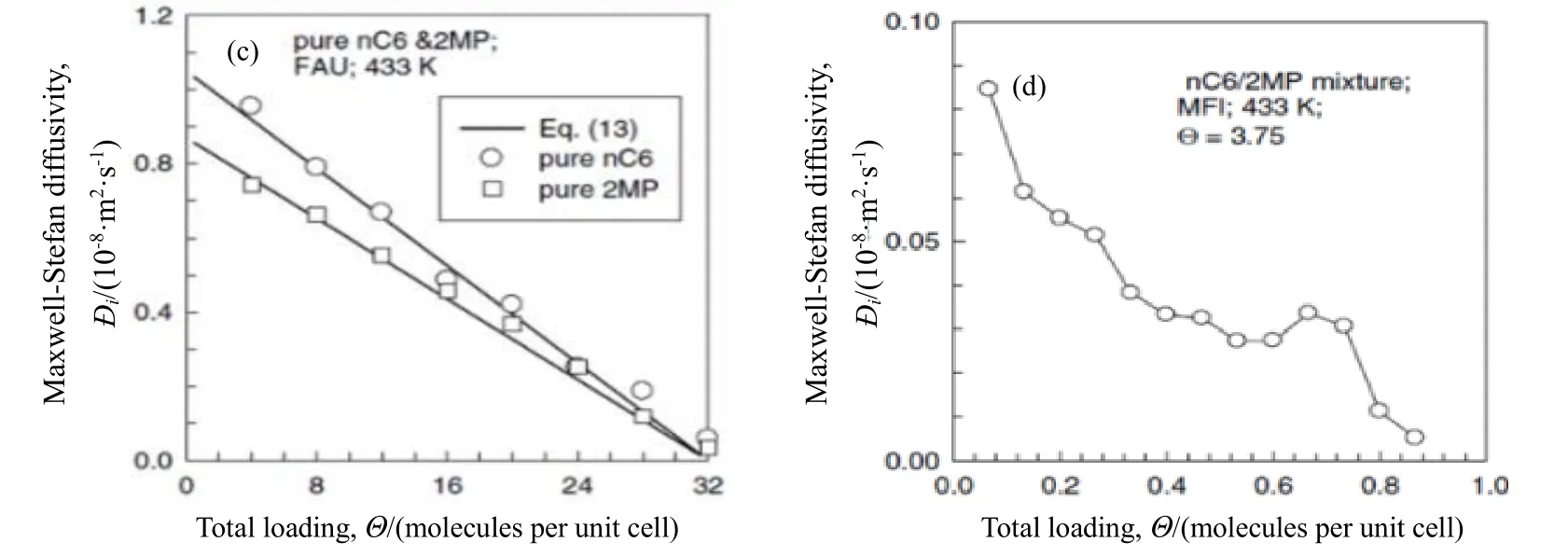
图6 支链烷烃在分子筛中扩散系数的变化[62]Fig.6 Changes of diffusion coefficients of branched alkanes in zeolites [62]

2.2 烯烃扩散

乙烯和丙烯等低碳烯烃是重要的基本有机化工原料，分子筛催化MTO反应提供了一条不依赖石油原料得到烯烃的替代生产路线[2-3]。工业上使用的SAPO-34分子筛的8元环结构是实现高双烯选择性的基础，其对乙烯和丙烯的扩散有显著影响[63]。本文主要总结温度、分子筛结构、酸性位和负载量等因素对低碳烯烃扩散性能影响的分子模拟研究进展。

2.2.1 温度对烯烃扩散性能的影响

Wang等[7]采用基于COMPASS力场的MD方法，研究了不同温度下乙烯和丙烯在4种不同分子筛（CHA，MFI，BEA和FAU）中的扩散行为，发现乙烯和丙烯的自扩散系数随着温度的升高而增大，且乙烯的自扩散系数高于丙烯的。乙烯与丙烯的自扩散系数比值与孔道结构和温度紧密相关，在8元环CHA分子筛中该比值在15以上，且温度越低比值越大，而在10元环和12元环分子筛中该比值在2左右。模拟研究发现丙烯在8元环CHA中的活化能垒超过20 kJ/mol，由此很好解释了小孔SAPO-34分子筛对丙烯等较大烯烃的扩散有较明显的限制作用，因此在MTO反应中表现出较高的双烯选择性。Combariza等[60]在研究中发现，丙烯在8元环分子筛（CHA和SAS）中的自扩散系数随温度的升高而下降。如前面所述，丙烯在8元环的小孔分子筛中扩散很慢，Cnudde等[40]采用常规力场MD方法模拟了乙烯在SAPO-34分子筛中的扩散，发现与AIUS分子动力学模拟相比较沿着扩散方向的自由能曲线相差不大；而常规力场MD模拟没有发现丙烯的扩散，这是因为动力学直径较大的丙烯扩散自由能垒明显高于动力学直径较小的乙烯。采用AIUS模拟可以更准确地定量分析自由能曲线受温度影响而产生的变化，有利于分析丙烯在8元环分子筛中的扩散。研究发现丙烯扩散自由能中的熵的贡献随着温度升高显著增加，从300 K时的19.1 kJ/mol到600 K时的37.7 kJ/mol，导致绝对自由能垒从300 K时的27.8 kJ/mol分别增加到450 K和600 K时的40.9 kJ/mol和49.4 kJ/mol，由于客体分子的动能随温度升高而增加，因此以kBT为单位的扩散自由能垒[见式（4）]比在低温时略有下降，总体扩散系数随温度升高而增加。

2.2.2 分子筛拓扑结构和刚柔性对烯烃扩散性能的影响

分子筛的拓扑结构对烯烃的扩散行为有重要影响，如烯烃的自扩散系数随着分子筛孔径的增大而增大，活化能垒随着分子筛孔径的增大而降低[7]。Ferri等[64]通过静态DFT计算和AIUS分子动力学方法模拟了乙烯和丙烯在CHA结构分子筛中的扩散，结果表明由从头算分子动力学（AIMD）方法得到的乙烯和丙烯的扩散自由能垒在SSZ-13分子筛中比在AlPO-34分子筛中要大（在623 K时，AlPO-34分子筛中乙烯和丙烯的自由能垒分别为38 kJ/mol和59 kJ/mol；SSZ-13分子筛中分别为49 kJ/mol和72 kJ/mol），且AlPO-34中的8元环窗口面积比SSZ-13中的增加约6%～7%，由此说明硅铝磷酸盐较大的8元环窗口面积和骨架柔性是影响SSZ-13和SAPO-34之间双烯选择性差异的重要因素。Ghysels等[65]采用完全柔性力场的MD方法讨论了乙烯和丙烯在一系列同等结构的铝硅酸盐和硅铝磷酸盐分子筛中的扩散，发现乙烯在AlPO/SAPO分子筛中的扩散比在SSZ/H-SSZ分子筛中更快，进一步研究发现窗口最小直径（dmin）这一结构参数不能完全解释分子穿过8元环窗口的次数（Ring Crossings）的所有趋势，因此引入了一个新的描述因子——可接近窗口面积（Accessible Window Area，AWA），将客体分子访问窗口区域和穿过窗口的次数通过指数形式的曲线联系起来，用来解释窗口直径的变化引起的扩散行为的改变，如图7所示。

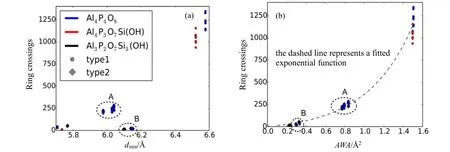
图7 450 K下乙烯分子100 ns内的运动轨迹中穿过SAPO-18分子筛8元环窗口的次数[65]Fig.7 Ring crossings of ethylene molecules through SAPO-18 zeolite in a 100 ns trajectory at 450 K [65]

Zhang等[66]采用基于CVFF力场的MD方法研究了1-丁烯在MCM-22分子筛中的扩散行为，发现在12元环孔道中的扩散比在10元环孔道中要快，并结合蒙特卡洛吸附能分析其原因是1-丁烯在12元环孔道中吸附能更高，容易吸附在12元环孔道中。烯烃的扩散除了与分子筛孔径大小相关外，还与分子筛的孔道形状相关。Liu等[67]采用基于COMPASS力场的MD方法研究了丙烯和丁烯在ZSM-5分子筛中的自扩散系数，发现丙烯和丁烯的自扩散系数在ZSM-5分子筛的直孔道方向的分量要高于在弯曲孔道方向的分量，从而表现出各向异性的扩散性能，而升高温度使丙烯、丁烯在2种孔道中扩散的差异性降低，MD模拟结果很好地解释了实验现象（见图8）。

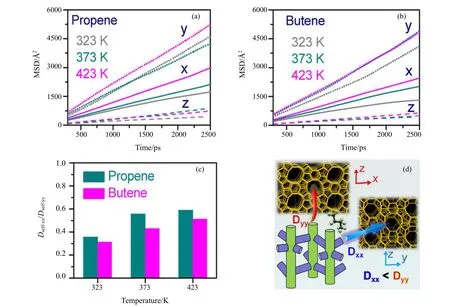
图8 丙烯和1-丁烯分子在MFI结构分子筛中扩散的MD模拟[67]Fig.8 Molecular dynamics simulations on the diffusion of propene and 1-butene molecules in MFI-structured zeolite[67]

此外，研究者对烷烃和烯烃在分子筛中的扩散性能进行了比较。Combariza等[60]采用经典力场的MD方法研究了丙烯在柔性骨架分子筛CHA和SAS中的扩散，发现丙烯在CHA中的自扩散系数比丙烷高2个数量级，这是因为丙烷在穿过窗口时的分子间相互作用能是丙烯的2倍。该研究还指出通过常规MD方法得到的自扩散系数是被低估的，需要通过TST方法进行改进。Boulfelfel等[9]采用TPS方法计算了乙烯和丙烯在柔性骨架LTA分子筛中的扩散系数，发现300 K下乙烯的扩散系数和乙烷相差不大，而丙烯的扩散系数是丙烷的4倍，通过分析分子扩散时窗口大小变化和在窗口的停留时间解释了这一现象。Verploegh等[44]采用dcTST方法研究发现，在ZIF-8分子筛中乙烯的扩散系数高于乙烷的，丙烯的扩散系数高于丙烷的。丙烷在非常规合成的多孔材料中的缓慢扩散归因于材料的结构缺陷，但为什么结构缺陷对丙烯扩散没有显著影响的原因尚不清楚。

2.2.3 酸性位对烯烃扩散性能的影响

包括酸中心强度和酸中心分布在内的分子筛酸性是影响分子筛催化反应性能的重要因素。Ghysels等[65]指出酸性位的存在会使乙烯的扩散变慢。而Cnudde等[40]采用AIUS分子动力学方法研究发现，Brønsted酸性位的存在可以促进乙烯和丙烯在SAPO-34分子筛中的扩散。采用AIUS方法模拟的烯烃通过SAPO-34分子筛中不同酸性位点的8元环的自由能曲线如图9所示，在450 K下，乙烯穿过不存在酸性位（type 0）的8元环时的自由能垒最高，约为30 kJ/mol，当穿过有1个酸性位（type 1）和2个酸性位（type 2）时，自由能垒降低到约为15 kJ/mol。丙烯在450 K和600 K下扩散垒受酸性位存在的影响也具有相似的规律。Cnudde等[40]通过由静态DFT计算得到的烯烃与酸性位间的特定相互作用进行解释：烯烃可以与酸质子相互作用形成π键络合物，由于烯烃在酸性分子筛中的吸附是一个动态过程，烯烃可以相当自由地穿过分子筛并在有限的时间内吸附在酸性位附近，然后再快速脱附。酸性位的存在不仅影响扩散能垒，而且影响自由能曲线的形状，这也是酸性位促进分子扩散的原因之一。Cnudde等[68]用相同的方法研究表明，虽然酸性位对烯烃的扩散有促进作用，但对烷烃的扩散并不敏感，并通过PFG-NMR实验证实了这一观点。该研究为通过改性酸中心分布来调变催化性能提供了思路。Smith等[39]通过DFT方法计算了乙烯、丙烯、顺式2-丁烯、反式2-丁烯、环丁烯、异丁烯、甲醇、苯、对二甲苯、四甲基乙烯和杜勒烯分子在含有酸中心的SSZ-13分子筛上的扩散能垒，发现较小分子（如乙烯和丙烯）、较大分子（如异丁烯）以及最大分子杜勒烯的能垒值分别约为70，200和350 kJ/mol。对于较大分子，扩散能垒可能与扩散分子的范德华半径相关，而具有较小能垒的小分子扩散能垒与范德华半径之间没有明显的相关性。

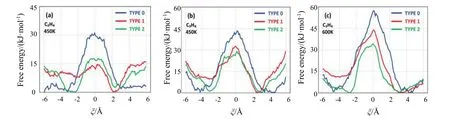
图9 采用AIUS方法模拟的烯烃通过SAPO-34分子筛中不同酸性位点的8元环的自由能曲线[40]Fig.9 Free energy profiles of olefins through 8-membered rings at different acid sites in SAPO-34 zeolite simulated by AIUS[40]

2.2.4负载量对烯烃扩散性能的影响

Verploegh等[44]采用dcTST方法研究发现，乙烯、丙烯和1-丁烯在全柔性ZIF-8分子筛中的扩散系数随负载量的增加而增大。Cnudde等[40]采用AIUS分子动力学方法对乙烯和丙烯在无酸性位的SAPO-34分子筛的8元环中的扩散随负载量增加而加快的现象进行了详细地分析，结果如图10所示，图中蓝色曲线表示没有额外丙烯分子的情况，丙烯分子在A笼和B笼中扩散的自由能曲线，红色曲线表示一个丙烯分子由A笼向含有两个丙烯分子的B笼中扩散以及该分子从B笼向空笼A扩散的自由能曲线，绿色曲线表示在A笼和B笼都额外含有两个丙烯分子的情况下，一个丙烯分子在A笼和B笼中扩散的自由能曲线。由图10可知，当丙烯分子从A笼向有2个丙烯分子存在的B笼扩散时，与没有额外丙烯分子的情况相比，正向扩散自由能垒（红色自由能曲线）几乎不受影响，自由能垒差值小于4 kJ/mol；而当从具有3个丙烯分子的B笼向空笼A扩散时，由于丙烯的负载量较高，降低了客体分子的稳定性以及构象的自由度，从而使得扩散自由能垒显著降低（与没有额外丙烯分子的情况相比，扩散自由能垒降低了近20 kJ/mol）；对于A笼和B笼都有2个额外丙烯分子的最高负载情况下，扩散自由能垒也显著降低（约为15 kJ/mol）。）

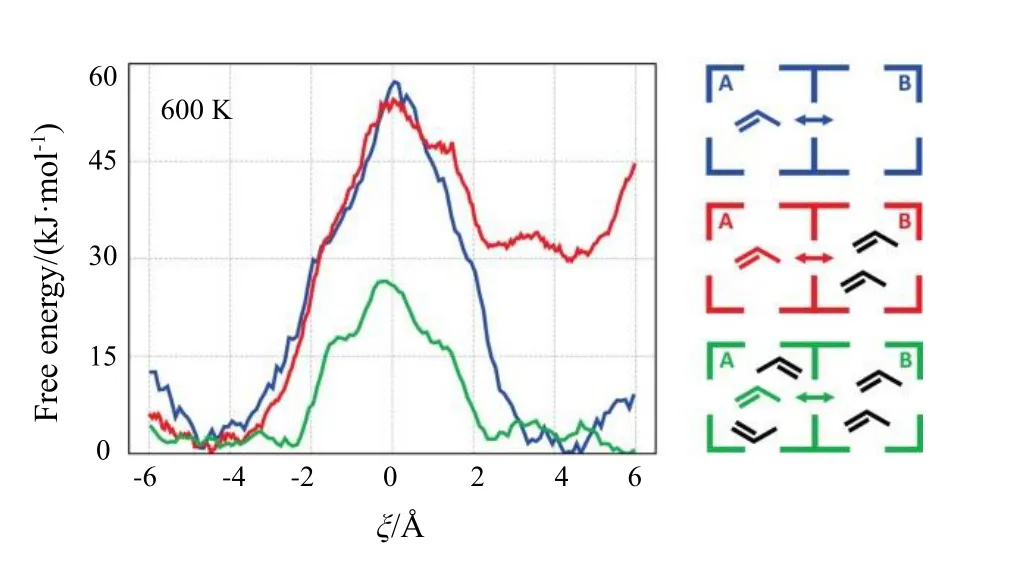
图10 采用AIUS模拟得到的丙烯通过SAPO-34分子筛中无酸性位的8元环扩散的自由能曲线[40]Fig.10 Free energy profiles for propene diffusion through a 8-ring without acid site in SAPO-34 zeolite from AIUS simulations[40]

Ahunbay[69]采用基于CVFF力场的MD方法研究了卤代烯烃在ZSM-5分子筛中的吸附和扩散，得到298 K下三氯乙烯和四氯乙烯的自扩散系数的数量级分别为10-10和10-11，这是首次对分子筛中的卤代烯烃扩散系数的预测，尽管对于CVFF力场的局限性还有待进一步改进。

2.3 芳烃扩散

很多研究者通过分子模拟研究强调了芳烃分子的形状和大小以及分子筛的孔尺寸和结构在有效控制分子扩散特性方面的重要性，大致可以将其分为两类。

（1）不同结构和孔径的分子筛对客体分子的择形性不同。Deka等[70]通过基于CVFF力场的能量最小化方法研究了邻、间、对-异丁基乙苯在大孔分子筛上的扩散能垒，发现对-异丁基乙苯在孔道型分子筛（丝光沸石、菱沸石）比在笼型分子筛（L沸石、8面沸石）的扩散能垒低、选择性高，并结合邻、间-异丁基乙苯在分子筛中的能垒大小得出对-异丁基乙苯选择性的优劣顺序为：丝光沸石＞菱沸石＞L沸石≈8面沸石。Waghmode等[71]研究了甲苯和二甲苯异构体烷基化过程中的扩散机理，通过研究二甲苯异构体与ZSM-5、丝光沸石和MCM-22分子筛的相互作用指出，当分子在ZSM-5分子筛的10元环和12元环孔道中扩散时，会通过有利和不利的吸附位点，使ZSM-5分子筛中对二甲苯比邻二甲苯和间二甲苯具有显著的选择性。Toda等[32]采用更为精确的核壳力场MD方法，研究了烷基转移反应中甲苯、三甲苯和二甲苯分子在包含10元环和12元环孔道的BOG，MSE，IWR，SFS，SOF和UWY纯硅分子筛中的扩散行为，表明UWY允许三甲苯在12元环孔道中反应，能够稳定过渡态，并有利于对二甲苯在10元环孔道中优先扩散。Toda等[72]进一步分析了UWY分子筛中交叉10元环和12元环孔道中甲苯、二甲苯和三甲苯的扩散机理，认为UWY是甲苯和三甲苯烷基转移反应中有较好应用前景的分子筛催化材料。

（2）客体分子在同一种分子筛中扩散的能垒与分子的尺寸和结构有关，从而体现出分子筛的择形性能。Waghmode等[71]研究指出甲醇、苯、甲苯和二甲苯在MCM-22分子筛中扩散能垒的大小是：二甲苯＞甲苯＞苯＞甲醇，与分子直径大小一致。Bu等[16]利用结合Hill-Sauer，OPLS和TraPPE多种力场的MD方法研究了二甲苯异构体在ZSM-5中的扩散机理，得到700 K时二甲苯异构体的自扩散系数比值为：对二甲苯:邻二甲苯:间二甲苯=83:3:1，而它们的临界分子直径相近（分别为6.7，7.4和7.3 Å），说明在分子筛孔径与分子大小相当的情况下ZSM-5中二甲苯异构体的自扩散系数主要是由空间位阻引起的。研究还发现，尽管甲苯和二甲苯的临界直径相同，但是二甲苯的自扩散系数是甲苯的2.5倍，这是因为分子取向影响了扩散速率。如图11所示，对二甲苯分子最长主轴与ZSM-5中直孔道方向之间的角度在0°附近分布最多，而甲苯分子则存在两个宽峰（0°和70°附近），表明在大部分模拟时间内，长轴尺寸较大的对二甲苯在孔径相对较小的分子筛中以其最长轴平行于孔道排列的方式运动，而长轴尺寸较小的甲苯在交叉区域频繁地旋转降低了扩散。

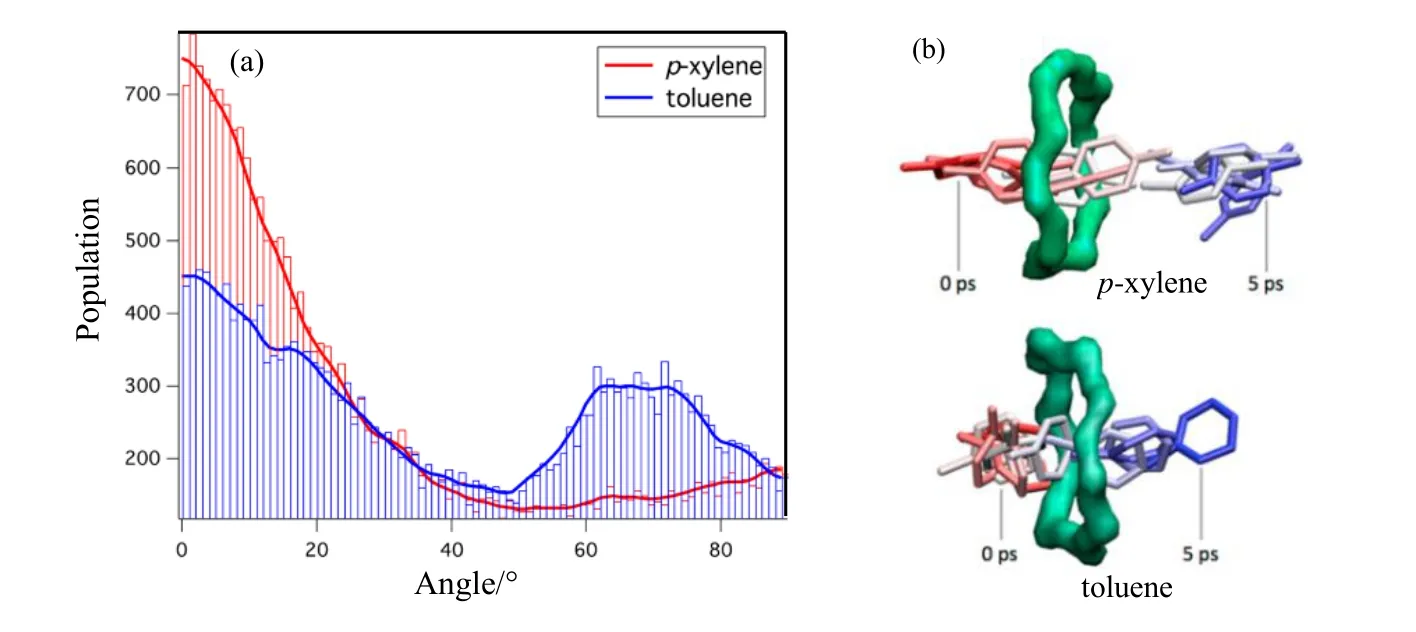
图11 在一定时间内甲苯/对二甲苯分子最长主轴与ZSM-5中直孔道方向之间的角度分布（a）以及对二甲苯和甲苯穿过直孔道的10元环的位置叠加（b）[16]Fig.11 Population of the angles between the longest principal axis of toluene/p-xylene molecule and the direction of the straight channel in ZSM-5 as a function of time(a) and superimposition of positions of a p-xylene and Toluene molecule crossing a 10-member ring via a straight channel(b) [16]

此外，Amirjalayer等[73]结合了DFT计算扩展了MM3力场，并采用新力场正确预测了苯在MOF-5中的扩散性能，提高了计算准确性。Liu等[27]通过基于TraPPE力场的MD方法对一系列分子筛进行了筛选，发现具有连续性交叉孔结构的SCM-15分子筛与传统交叉孔结构（非连续离散型交叉孔道，如MFI）性能完全不同，对二甲苯在高负载下依旧保持较高的扩散性能。在低负载情况下，对二甲苯主要沿着具有强吸附位点的非连续（离散）交叉孔方向扩散；随着负载量增加，对二甲苯逐渐吸附到具有较低扩散能垒的连续交叉孔方向，有效克服了高扩散能垒带来的不利因素。Bu等[74]采用MD方法研究了苯、萘和蒽在多级孔ZSM-5分子筛中的扩散行为，考察了温度和介孔大小对所选客体化合物扩散性能的影响。研究表明，在低温下，分子主要在微孔和介孔ZSM-5的外表面上进行扩散，而在高温下分子基本上是沿中孔进行扩散的。Sastre等[75]通过MD方法模拟纯硅ZSM-5分子筛中苯的吸附和释放速率，建立了同时包含分子筛表面扩散和内部扩散的模型，表明扩散动力学是由表面阻力（外表面的孔阻塞）和晶胞内扩散阻力的组合效应控制的，分子筛晶体表面的有限渗透率（即表面阻力）为分子吸附和扩散提供了动力。

3 多组分扩散

研究多组分扩散的方法包括MD、KMC以及适用于多组分扩散的M-S理论等。由于多组分扩散不仅包括主客体之间的相互作用，还包括不同客体分子之间的相互作用，同时不同客体分子之间的扩散动力学差异，使得多组分扩散的研究具有很大的挑战性，需要从扩散机制、相互作用、构效关系等多方面进行探讨。

3.1 相关效应

Skoulidas等[48-49,76-77]通过KMC，MD和M-S理论方法深入研究了多组分混合物的扩散机理，发现混合物中有些分子的扩散系数比纯组分增大，有些分子的扩散系数则减小，认为不同混合物组成分子的加速/减速可归因于相关效应（correlation effect），这是混合物分子跳跃快慢不同改变了附近空位情况而引起的。相关效应会导致扩散较快的分子减速，而运动较慢的分子加速。例如，MFI结构硅质岩中CH4/CF4混合物中CH4的扩散随CF4的加入逐渐变慢，而CF4的扩散随着CH4的加入逐渐变快[48,76-77]；在交叉孔道MFI、一维孔道MOR以及笼型结构FAU分子筛中都发现由相关效应引起的甲烷/丙烷混合物的加速和减速比甲烷/乙烷混合物的更严重[53]；Liu等[45]通过MD和M-S方法也发现甲烷与乙烷、丙烷或正丁烷共混时扩散系数降低的现象；Yue等[78]采用MD方法研究了苯/CO2混合物在MFI分子筛中的扩散行为，发现CO2分子在混合物中的自扩散系数比纯组分体系低1个数量级，这种相反的行为主要是由较大的共吸附苯分子的阻塞或捕获效应引起的。Krishna等[49]研究指出相关效应的强度不仅与负载量紧密相关（即在高负载量下相关效应变得更强，加速/减速效应也会增加），而且还取决于分子筛的拓扑结构。

3.1.1 负载量和温度对混合物扩散性能的影响

多个研究证明，混合物扩散性能随负载量的变化以及扩散性能对负载的依赖性随温度的变化与纯组分相比相差不大[12,49,77]。但也有相反的情况，Yue等[78]发现苯/CO2混合物在MFI分子筛中，CO2的扩散系数随着CO2的加入而增加，这与纯CO2体系的观察结果相反，研究还发现在接近饱和的高负载量下，由于客体分子的熵效应而出现扩散速率的不同。Smit等[77]采用构象偏倚蒙特卡洛方法（Configurational-bias Monte Carlo，CBMC）、KMC和MD方法研究线性和支化烷烃在MFI分子筛中的吸附和扩散行为，发现在高负载量（饱和负载量，Θmix）下构型熵效应导致己烷异构体的等物质的量混合物在MFI分子筛中的吸附量大小为：线性＞单支化＞双支化（见图12），从而可以从单支链烷烃中分离出双支链烷烃，研究还发现熵效应和相关效应存在相互竞争的关系。Hussain等[56]通过MD方法研究了甲烷、乙烷及丙烷的混合物在MFI分子筛中的扩散，发现对于大小相似的分子（例如甲烷/乙烷和丙烷/乙烷的混合物，分子的自扩散系数随着负载量的增加而降低。由于在更高的负载量下尺寸熵效应占主导地位，导致尺寸较小的组分更容易分离出来。对于具有不同尺寸大小的二元混合物，例如甲烷/丙烷，虽然较小的甲烷在整个负载范围内扩散得更快，但由于相关效应占主导，随着负载量的连续增加，甲烷的自扩散系数逐渐降低，而丙烷的自扩散系数在整个负载范围内几乎保持不变。

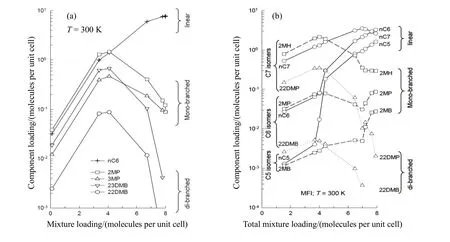
图12 CBMC模拟得到的MFI分子筛中等物质的量直链烷烃和支链烷烃混合物各组分负载量随总混合物负载量的变化[77]Fig.12 Component loadings simulated by CBMC for equimolar mixture of straight chain alkanes and branched chain alkanes in MFI zeolite as a function of total mixture loading [77]

混合物在分子筛中的扩散性能还受到温度的影响。Hussain等[56]研究指出，当温度升高时分子之间的相关效应更加明显。对于甲烷/乙烷/丙烷3元混合物，300 K时甲烷在孔道内扩散得更快，而400K时乙烷在弯曲孔道中的自扩散系数最高，这可能是由于晶格振动有助于改变分子筛孔道中客体分子的扩散行为。前面提到，在MFI和TON分子筛的限制下，长链分子正十二烷在高温下发生弯曲而导致“热阻效应”，自扩散系数随温度的升高而降低，可以将其从短链烷烃中分离开来[58]。

3.1.2 分子筛拓扑结构对多组分扩散性能的影响

Krishna等[53]研究发现，相关效应强烈依赖于分子筛的拓扑结构，在不同结构的分子筛中混合物的扩散选择性不同，甲烷、乙烷和丙烷的混合物在被8元环窗口隔开的笼型分子筛中（CHA，DDR，ERI，LTA）的相关效应可以忽略不计，而交叉孔道结构（MFI，ISV，BEA）和一维孔道（AFI，TON，FER，MOR，LTL）中的二元甲烷/乙烷和甲烷/丙烷混合物，由于存在扩散更迟缓的乙烷或丙烷，扩散性能更强的甲烷分子的扩散系数显著降低，运动缓慢的分子扩散性能得到增强。van Baten等[62]发现己烷异构体和丁烷烃异构体在不同结构分子筛中扩散系数的大小会发生逆转，这为不同结构分子的扩散和分离提供了理论依据。

混合物的扩散系数与窗口直径的大小直接相关。Krishna等[20]采用MD方法的研究表明，由3.4～4.6 Å的8元环窗口隔开的DDR，CHA，LTA，ITQ-29和TSC分子筛可用于分离各种混合物，例如CO2/CH4、CO2/H2、H2/CH4和丙烷/丙烯，且窗口孔径越小，混合物自扩散系数的差异越大，越容易分离。Krishna等[13,54]还研究指出，MOFs，COFs和CNTs等其它材料中甲烷及其混合物的扩散适应于相关相应。Liu等[79]通过EMD方法研究了CO2/CH4和CH4/H2混合物在ZIFs分子筛中的扩散行为，表明CH4/H2混合物的扩散符合相关效应，即CH4的自扩散系数随着CH4/H2混合物中H2负载量的增加而增加，而H2的自扩散系数随着CH4负载量的增加而减少；但CO2/CH4混合物的扩散则相反，CH4的自扩散系数基本上与CO2/CH4混合物中CO2的负载量无关，而CO2自扩散系数随着CH4负载量的增加而降低，CH4的自扩散系数明显大于CO2的自扩散系数。这种不寻常的现象可以用电荷相互作用导致的吸附位点偏好差异来解释。

3.2 基于多组分扩散的分子筛积炭失活

多组分扩散除了与产物的选择性和吸附分离有关外，还可以研究分子筛催化反应的积炭失活机制。Liu等[35]通过MD方法探究了ZSM-12和ZSM-22在催化MTO反应中各物质的自扩散系数，指出分子筛拓扑结构引起的扩散差异可以导致不同的催化反应。在MTO反应中，甲醇和烯烃在ZSM-12和ZSM-22分子筛上都能自由扩散，但在ZSM-12孔道（6.0 Å）中的自扩散系数是ZSM-22（5.7 Å）中的2～3倍左右（见图13），因此在ZSM-22中更慢的扩散造成更长的接触时间会促使烯烃和甲醇的进一步反应；对于芳烃循环，孔道较大的ZSM-12限制住的是四甲基苯，其进一步甲基化得到的五甲基苯是高活性的中间体，可以通过消去或侧链路线生成烯烃，而ZSM-22分子筛限制住的是三甲基苯，其进一步甲基化得到的四甲基苯活性并不高。因此由分子筛拓扑结构导致的不同分子的扩散行为影响了双循环反应路线。

图13 不同分子的自扩散系数和等量吸附热的关系（a）以及分子筛中客体分子的自由能曲线（b）[35]Fig.13 Relation of the diffusion coefficients and isosteric heat for different molecules(a) and free energy for guest molecules in zeolites(b)[35]

Gao等[80]开发了一种基于双循环机制和M-S扩散理论的建模方法，研究了SAPO-34分子筛MTO过程中的反应和扩散，结果表明该模型可以预测烯烃循环和芳烃循环反应过程中的活性积炭（activated coke）和非活性积炭（non-activated coke）的演化，非活性积炭的形成会导致SAPO-34分子筛内部的孔隙堵塞，并在不同程度上限制了不同客体分子的扩散。Cnudde等[40]采用更为准确的AIUS分子动力学方法模拟了接近真实MTO环境中，即在甲醇和不同芳烃物种（六甲基苯、甲苯）存在下，丙烯在SAPO-34分子筛中的扩散行为，并进行了自由能分析。结果表明，丙烯进入充满六甲基苯和甲醇的笼中会受到强大的阻力，因此丙烯立即扩散到相邻的空笼子中；在甲苯存在的情况下，丙烯进入笼子的障碍虽然也相对较大，但仍然有相对较高的移动性，而且丙烯可以与甲苯吸附在同一个笼子中至少80 ps。并根据模拟结果认为，如果乙烯和丙烯在包含烃池物种的笼子中形成，将很容易扩散到没有烃池物种的下一个笼子中，因此空笼的存在可防止催化剂堵塞。

4 结语和展望

研究烷烃、烯烃和芳烃等客体分子在分子筛中的扩散行为是分子筛领域的重要方向，关系到分子筛择形催化、吸附分离、催化材料失活和稳定性等关键问题。以分子动力学为代表的分子模拟技术在分子筛扩散研究中发挥极为重要的作用，可以在分子水平上深入研究扩散机制，并计算得到扩散动力学参数。本工作总结了经典和从头算分子动力学、过渡态理论、动力学蒙特卡罗等模拟计算方法在分子筛扩散研究中的应用，综述了温度、负载量、分子筛孔道结构和刚柔性、酸性位等因素对限域条件下单组分和多组分碳氢化合物分子扩散性能的影响。随着高性能计算能力和扩散动力学模拟方法的进一步发展，使得模拟更为复杂的体系和更真实的条件成为可能。a）以从头算伞形取样和基于机器学习势函数为代表的高精度分子模拟方法在探索“慢”扩散过程上比传统过渡态理论方法更为准确，且适用于研究复杂分子筛结构模型。b）分子筛拓扑结构对分子扩散行为有重要影响，特别是产物的择形与扩散息息相关，如何能够通过模拟研究总结出分子筛拓扑结构与扩散动力学参数之间的定量关系，并提出简单有效的衡量扩散性能的结构描述因子，将对分子筛材料设计和筛选提供重要指导意义。c）分子筛中多组分扩散是一个难点，不仅关系到主客体之间的相互作用，还关系到不同类型客体分子之间的相互作用，精确描述它们之间的相互作用至关重要。d）在分子筛催化反应中，反应物、产物以及中间体的扩散与基元反应之间紧密相关，如何将反应动力学与扩散动力学联系起来将是分子筛催化反应多尺度模拟研究的重要内容。