基于粒子群优化算法的烯烃聚合反应动力学参数估计

田 洲，洪华平，石 杰，王振雷

1.华东理工大学能源化工过程智能制造教育部重点实验室，上海 200237；

2.同济大学上海智能科学与技术研究院，上海 200092；

3.中国石油化工股份有限公司镇海炼化分公司，浙江 宁波 315207

聚烯烃大分子链中不同类型单体的连接方式导致了链结构的多样性，使其具有丰富的物理特性。聚烯烃产品的宏观性能取决其微观链结构分布，如分子量分布（molecular weight distribution，MWD）、化学组成分布（chemical composition distribution，CCD）、短链分支（short chain branch，SCB）和共聚单体序列长度分布（comonomer sequence length distribution，SLD）等[1-2]。聚合反应动力学对生成聚合物的微观结构有着重要影响，但是目前缺少直接有效的方法测量动力学参数，尤其是多活性位Ziegler-Natta催化剂催化烯烃聚合过程。

动力学参数估计是烯烃聚合过程建模与优化的重要步骤。目前，动力学参数估计的方法主要分为两种：一种是通过烯烃聚合反应动力学小试实验获得反应速率曲线，采用拟合回归方法估计出链活化、链增长、链失活等表观聚合反应速率常数[3-5]；另一种是通过聚合物链结构检测表征技术获得链结构分布曲线如MWD和SCB等，结合操作条件、聚合产率等对该曲线做去卷积分析获得详细的反应动力学参数[6-8]。郑征等[9]由丙烯/1-丁烯共聚实验过程中的丙烯消耗速率估算了不同类型活性中心的活化、丙烯链增长以及链失活的速率常数。Chen等[10]对乙烯/α-烯烃聚合反应中不同停留时间下乙烯消耗速率、聚合物产率以及MWD采样分析，运用最小二乘方法估计了聚合反应动力学参数。Zhang等[11]提出了一种多步估计乙烯均聚反应动力学参数的方法。安许锋等[12]利用改进的广义动态模糊神经网络估计了活性位个数、数均分子量等参数，并实现了分子量分布的软测量。Hornchaiya等[13]对实验测得乙烯/1-己烯的二元MWD和CCD同时去卷积分析，实现了对催化剂活性位个数、聚合物数均分子量以及平均共聚组成的估计，但未对动力学参数进行计算。多活性中心催化剂作用下，共聚反应动力学参数如竞聚率、交叉链增长速率常数等参数估计一直是具有挑战性的问题。Al-Saleh等[14]对由多活性中心催化剂所生成聚合物的SLD估计了竞聚率。Mehdiabadi等[15]基于单体消耗速率曲线模型，使用Mayo-Lewis方法和交叉链增长速率估计了聚合过程不同单体的竞聚率。但以上两者均未对交叉链增长等共聚反应动力学参数直接估计。为了克服均聚物MWD去卷积分析中采用常规方法（如非线性最小二乘法）需要精确初始值的问题，本团队石杰等[16]提出采用免疫算法（IA）对分子量分布曲线进行去卷积分析，获得了各活性中心产生聚合物的质量比以及数均分子量，也未对动力学参数进行估计计算。

聚烯烃的MWD，SCB和CCD等微观链结构与聚合反应动力学参数密切相关。目前聚烯烃工业中Ziegler-Natta催化剂占比80%以上，其多活性中心的特征以及复杂的动力学行为使得其聚合反应动力学参数估计，尤其是共聚体系的动力学参数估计，仍然是挑战性的课题。本研究从烯烃聚合反应原理出发构建聚烯烃MWD，SCB和CCD的预测模型，以及均聚、共聚反应动力学参数估计的优化模型。以三种不同微观链结构为优化目标，以动力学参数作为优化变量，采用IA算法和粒子群优化算法（PSO）直接求解聚合反应动力学参数，并比较两种算法的求解效果。

1 动力学参数估计优化模型构建

1.1 烯烃聚合反应动力学

Ziegler-Natta催化剂催化烯烃聚合反应本质上是多活性位配位聚合反应，基元反应包括链活化、链增长、链转移和链失活，典型的共聚反应式如下：

链活化：

链增长：

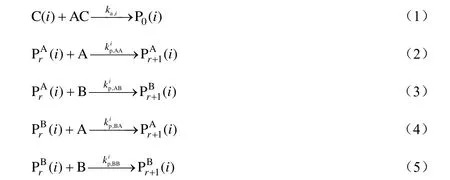
链转移：

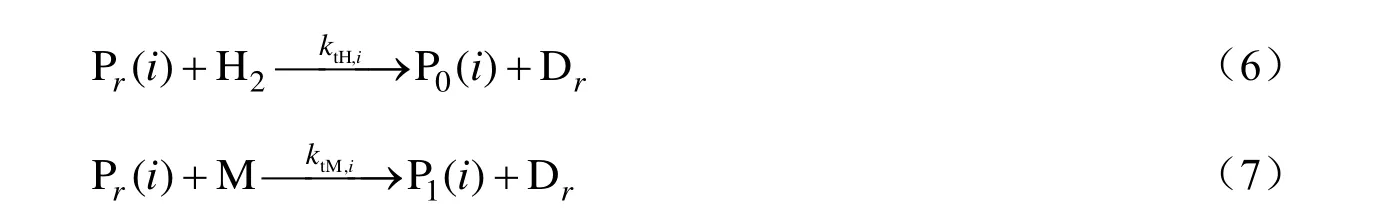
链失活：

式中：i为催化剂第i个活性位，C为潜在催化剂活性中心，AC为助催化剂，A为聚合单体，B为共聚单体，M为单体（包括A和B），Pr为不分链末端单元类型的链长为r的活性链，PrA为链末端为单元A的链长为r的活性链，PrB为链末端为单元B的链长为r的活性链，Dr为链长为r的死链，Cd为失去活性的催化剂活性中心。聚合反应动力学参数ka,i，kpi，ktH,i，ktM,i和kd,i分别为第i活性位的链活化速率常数、链增长速率常数、向氢链转移速率常数、向单体链转移速率常数和链失活速率，其中ka,i，kpi，kd,i与聚合反应速率相关，kpi，ktH,i，ktM,i与分子量分布、短支链分布和共聚组成分布等聚合物链结构密切相关，是本研究参数估计的对象。

对于共聚合反应，单体竞聚率为：

式中：rA和rB为单体竞聚率，无因次；kp,AA，kp,AB，kp,BB和kp,BA为交叉链增长速率常数，L/(mol·s)。

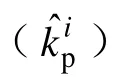
其中：

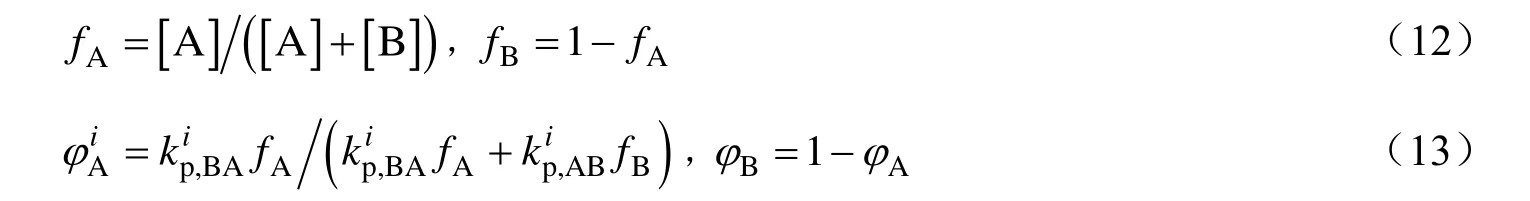
式中：[A]和[B]分别为聚合单体和共聚单体的浓度，mol/L；fA和fB分别为单体A和B在反应体系中的摩尔分数；φA和φB分别为以单体A和B摩尔分数表示的瞬时共聚组成。

1.2 分子量分布模型

MWD是聚合物基本微观链结构质量指标之一，其分布的多样性使得聚合物具有不同的物理特性与化学性质。由多活性中心Ziegler-Natta催化剂制得的聚合物MWD由多个活性中心加权求和所得，因而一般具有较宽的分子量分布。每一个活性中心产生的聚合物MWD都服从Flory-Schulz最可几分布[1]：

式中：wMW,i为第i个活性位所生成聚合物的分子量分布；Mn,i为聚合物的数均分子量，g/mol；MW为聚合物的分子量（自变量），g/mol。其中，Mn,i与聚合动力学速率常数的关系为：

式中：[M]为单体总浓度（[A]+[B]），mol/L；[H]为聚合体系中氢气浓度，mol/L。

1.3 短支链分布模型

不同活性中心催化乙烯/α-烯烃共聚反应表现出不同的α-烯烃插入能力，因此总聚合物中共聚单体含量随聚合物的分子量而变化。多活性中心催化剂所生成的聚合物的共聚组成（FB,MW）与分子量分布的关系如下：

式中：NS为催化剂活性中心数；FB,i为第i个活性中心生成聚合物的平均共聚单体组成。体积排除色谱结合红外分析（SEC-IR）表征技术可提供每1 000个碳原子的短链分支数（SCB/1000C）的信息。对于已知的共聚单体，该数据可以直接转化为共聚单体组成[1]：

式中：FB为聚合物中B的含量，无因次；nc为共聚单体中碳原子数目。

1.4 共聚组成分布模型

共聚组成分布（CCD）描述共聚物中平均共聚单体含量的分布，反映了分子间的异质性。CCD的分布模型采用Stockmayer方法[17]，如式（18）所示：

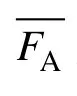
对公式（18）中的分子量MW进行积分可得一维CCD关于聚合单体A含量[W(FA)]的表达式：

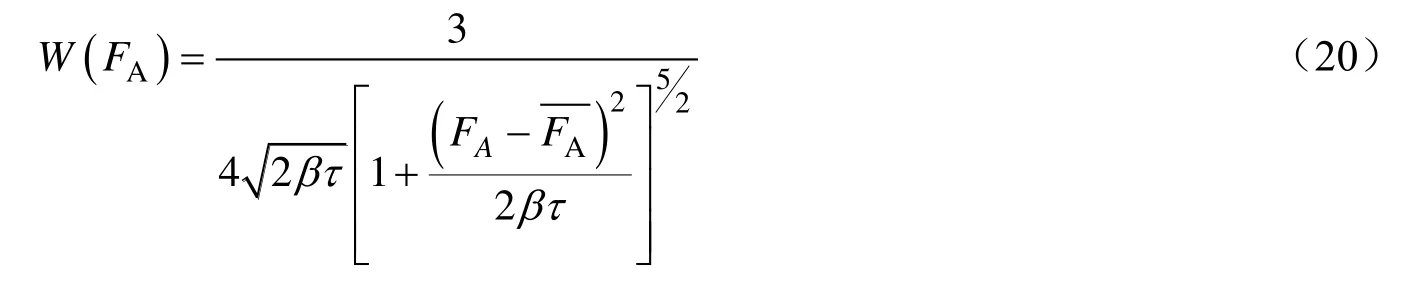
式中：τ为链转移速率与链增长速率之比，即数均分子量的倒数，Mn,i-1。

多活性中心催化剂制备的聚烯烃二维CCD为每一个活性中心所生成聚合物CCD的加权求和：

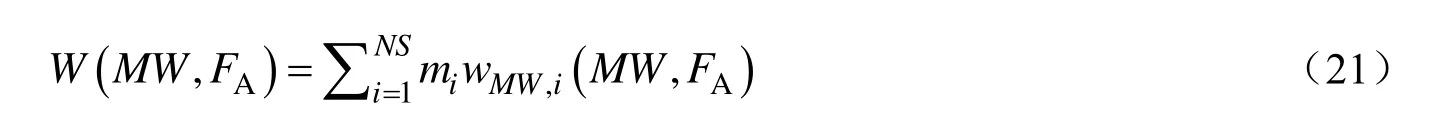
式中：mi为每个活性中心所生成聚合物占的质量分数。

1.5 优化目标函数

动力学参数估计与去卷积分析密切相关，实质上即为优化问题的构建与求解。不同的微观链结构去卷积分析具有不同的优化目标函数。以MWD曲线作为去卷积分析对象，其优化目标函数（E）为：

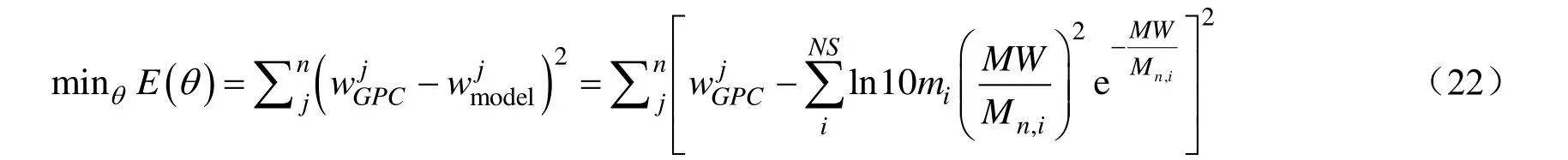
以MWD和SCB作为去卷积分析对象，其优化目标函数为：

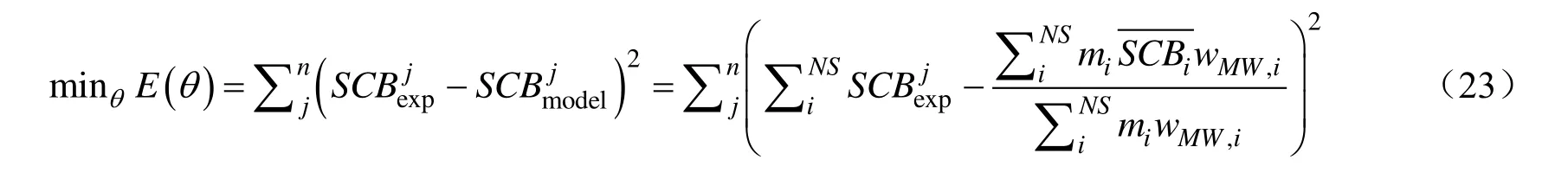
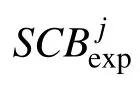
以MWD和CCD作为去卷积分析对象，一维CCD与二维CCD优化目标函数（χ2）如下：

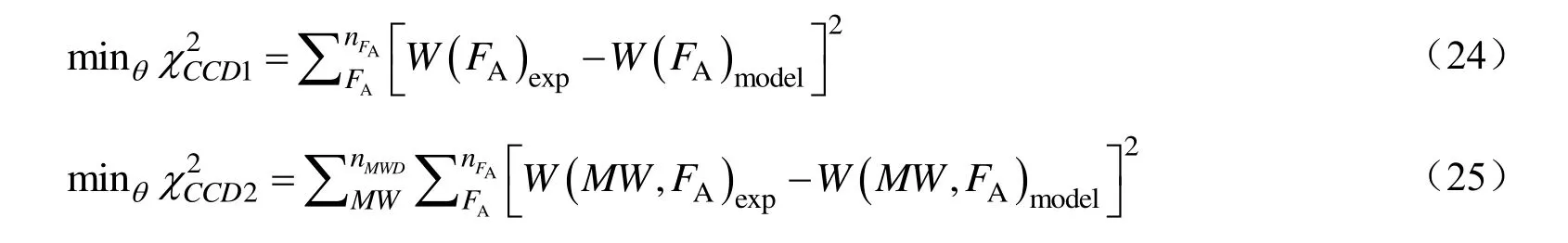
式中：θ可取mi，Mn,i，FA,i和βi；nAF为FA采样点数；nMW为分子量MW采样点数；W(FA)exp与W(FA)model分别为实验所测与模型预测的一维共聚组成分布曲线；W(MW,FA)exp与W(MW,FA)model为实验所测与模型预测的分子量与共聚组成二维分布曲线。

2 粒子群优化算法

粒子群优化算法的主要步骤为（1）初始化：初始化粒子种群，随机给定粒子的速度和位置；（2）计算粒子适应度：根据适应度函数，计算每个粒子的适应度值；（3）求解个体和群体最优值：对每一个粒子，将其当前的适应度值与历史最优值对比，若优于历史最优值，则更新种群的全局最优解；（4）根据公式更新粒子的速度和位置信息；（5）终止：判断是否满足结束条件，不满足则转步骤（2），满足则结束计算，当前的全局最优位置则是粒子种群的最优解。其中，在PSO算法中第i粒子的速度和位置由如下公式更新：

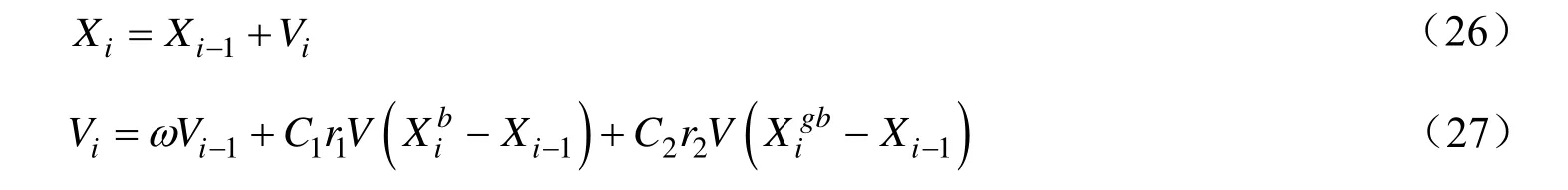
式中：Xi为粒子种群i的位置；Vi为粒子种群i的速度；n为粒子种群的维数；C1和C2为大于0的速度常数；ω为速度的惯性权重，代表前一个粒子的速度对当前粒子速度的影响比重；r1和r2为0～1的随机变量；Xb为当前粒子的个体最优解；Xgb为整个种群的全局最优解。

从公式（27）可知，粒子的更新速度主要包含记忆项、自身认知项和种群认知项三个方面。记忆项主要代表粒子的上一次速度和位置对当前速度的影响；自身认知项代表从当前粒子的位置到粒子自身最优位置的方向矢量；种群认知项表示当前粒子的位置到粒子种群最优解的方向矢量。

3 结果与讨论

本文计算所需反应体系组分浓度数据以及MWD，SCB和CCD数据取自文献[18]，催化剂浓度[C]、助催化剂浓度[AC]、聚合单体浓度[A]、共聚单体[B]以及氢气浓度[H]等组分浓度如表1所示。

表1 反应体系中的组分浓度[18]Table 1 Concentration of components in reaction system[18]

3.1 以MWD为目标的均聚动力学参数估计

单独对均聚物MWD分子量分布曲线进行去卷积分析可以估计催化剂活性位中心数目、每个活性中心生成聚合物的质量分数（mi）及其数均分子量[16]。在此研究基础上，数均分子量采用公式（15）表示，以MWD作为优化目标函数，以mi，kp和ktH作为优化变量，直接采用IA算法和PSO算法进行求解，结果如图1所示。由图1可知，总聚合物MWD是四个活性中心所生成聚合物MWD的加权组合。活性中心从1到4，聚合物的数均分子量依次增大。活性位2与活性位3的分子量占整个聚合物的比重较大，与催化剂本征特性相关。采用IA算法去卷积分析的结果在分子量较高时模型与实验数据误差较大，意味着对活性位4所生成聚合物的质量分数预测值偏高，而采用PSO算法去卷积分析的结果在整个分布曲线上与实际吻合程度较好。

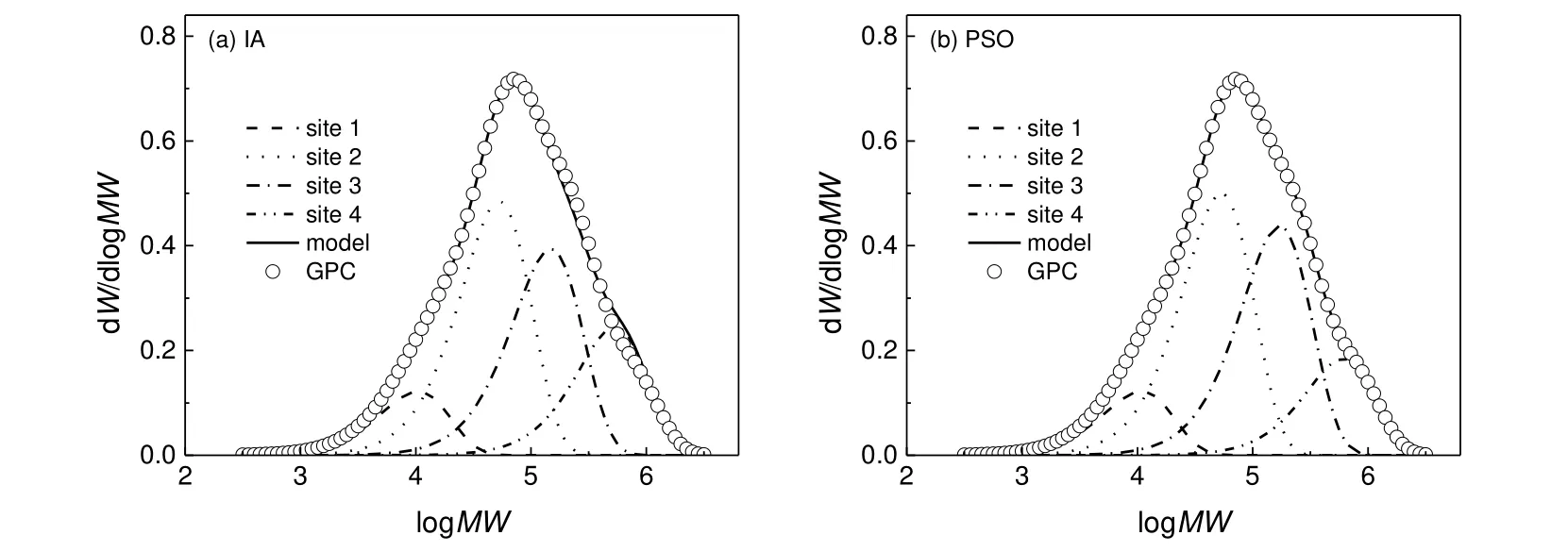
图1 以MWD为目标的去卷积结果Fig.1 Results of deconvolution with target MWD

以MWD为目标的均聚动力学参数估计的详细结果见表2。由表2可知，采用IA算法获得的活性中心4所生成聚合物的占比为0.196 6，比实际值0.148大近33%，验证了前面对分子量分布曲线预测的判断。采用PSO算法估计的mi，kp，ktH与实际数据的最大误差均比采用IA算法求解的结果误差小，表明了PSO算法在此优化问题求解中的优越性。

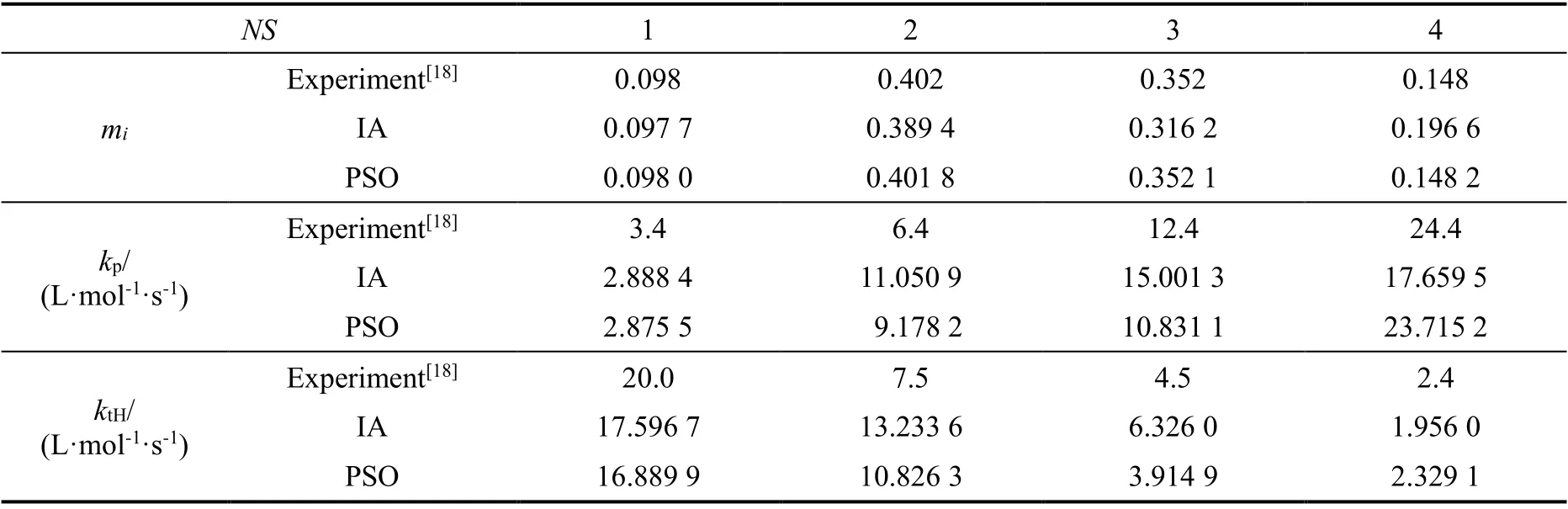
表2 以MWD为目标的均聚动力学参数估计结果Table 2 Estimated kinetics parameters of homopolymerization with target MWD

3.2 以MWD-SCB为目标的共聚动力学参数估计

对于聚乙烯共聚物而言，由于共聚单体的加入改变了聚合物的链结构，对聚合物的性能产生至关重要的影响。例如高密度聚乙烯，加入α烯烃后（1-丁烯、1-己烯、1-辛烯），由于聚合物链中引入了短支链SCB，对聚乙烯链的结晶、链缠绕以至聚合物聚集态结构产生影响，进而对聚合物的长期力学性能（如耐慢速裂纹增长性能）起决定性作用。SCB是聚乙烯类共聚物重要微观链结构指标之一。以MWD-SCB曲线作为优化目标函数，即以模型预测的MWD和SCB和实验曲线之间的误差平方和最小为目标，以共聚反应动力学参数为决策变量进行优化求解，去卷积分析的结果如图2所示。由图2可知，由于在MWD去卷积的基础上加入了对SCB的考虑，使得估计的动力学参数能够同时满足聚合物的MWD和SCB。随着活性位从1到4变化，聚合物的数均分子量依次增大，而平均短支链逐渐减小，也即聚合物的平均共聚组成随分子量的变大而逐渐减小，表明产生高分子量聚合物活性中心的共聚能力较弱。相较IA算法，采用PSO算法的模型预测MWD-SCB结果与实际更为吻合。

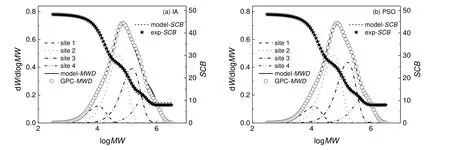
图2 以MWD-SCB为目标的去卷积结果Fig.2 Results of deconvolution with target MWD-SCB

表3给出了以MWD-SCB为目标的共聚动力学参数估计结果。由表3可知，采用PSO算法估计每个活性中心kp,AA最大相对误差不超过5%，而IA算法则为23.5%；采用PSO算法估计每个活性中心ktH最大相对误差6.39%，IA算法则为18.3%。总体上，以MWD-SCB为目标采用PSO算法预测估计动力学参数的结果优于IA算法的值。需要指出的是，原文献[18]中对kp,AB和kp,BB在每个活性中心的数值都设置为1，这里可以作为等式变量约束减少优化变量的个数直接从竞聚率求出另两个交叉链增长速率常数kp,AA和kp,BA。

表3 以MWD-SCB为目标的共聚动力学参数估计结果Table 3 Estimated kinetics parameters of copolymerization with target MWD-SCB

续表3

3.3 以MWD-CCD为目标的共聚动力学参数估计

CCD是表征共聚物微观链结构的另一重要参数，描述共聚物在聚合物中的含量分布。图3是采用不同算法对MWD和CCD曲线去卷积分析的结果。由图3可知，聚合物中共聚单体B含量基本分布为0～0.15，并在共聚单体B含量为0～0.05时呈现双峰分布特征，而且共聚单体B含量处在此区间的聚合物较多。由图3（a）和图3（b）可知，同时以MWD和CCD作为优化目标，采用IA算法去卷积分析得到的MWD与GPC实测的MWD相去甚远，得到的CCD也不能准确描述实际CCD，尤其FA为0.85～0.95时的预测值与实际值之间差距较大。但从图3（c）和图3（d）可以看出，采用PSO算法的去卷积分析得到的MWD和CCD曲线与实际值吻合较好，表明该方法可以准确描述两者的分布趋势。

图3 以MWD-CCD为目标的去卷积结果Fig.3 Results of deconvolution with target MWD-CCD

表4是以MWD-CCD为优化目标的共聚反应动力学参数估计结果。由表4可知，采用PSO算法预测的各活性中心产生聚合物质量比例、数均分子量、平均共聚组成的最大相对误差分别不超过3%，10%和1%，预测精度均远高于IA算法。采用PSO算法估计的交叉链增长速率常数、向氢气链转移速率常数的精度也高于IA算法，表明PSO算法在直接以MWD-CCD为目标的动力学参数估计优化求解过程中表现优异，可以作为多活性位烯烃聚合反应动力学参数估计的通用方法。

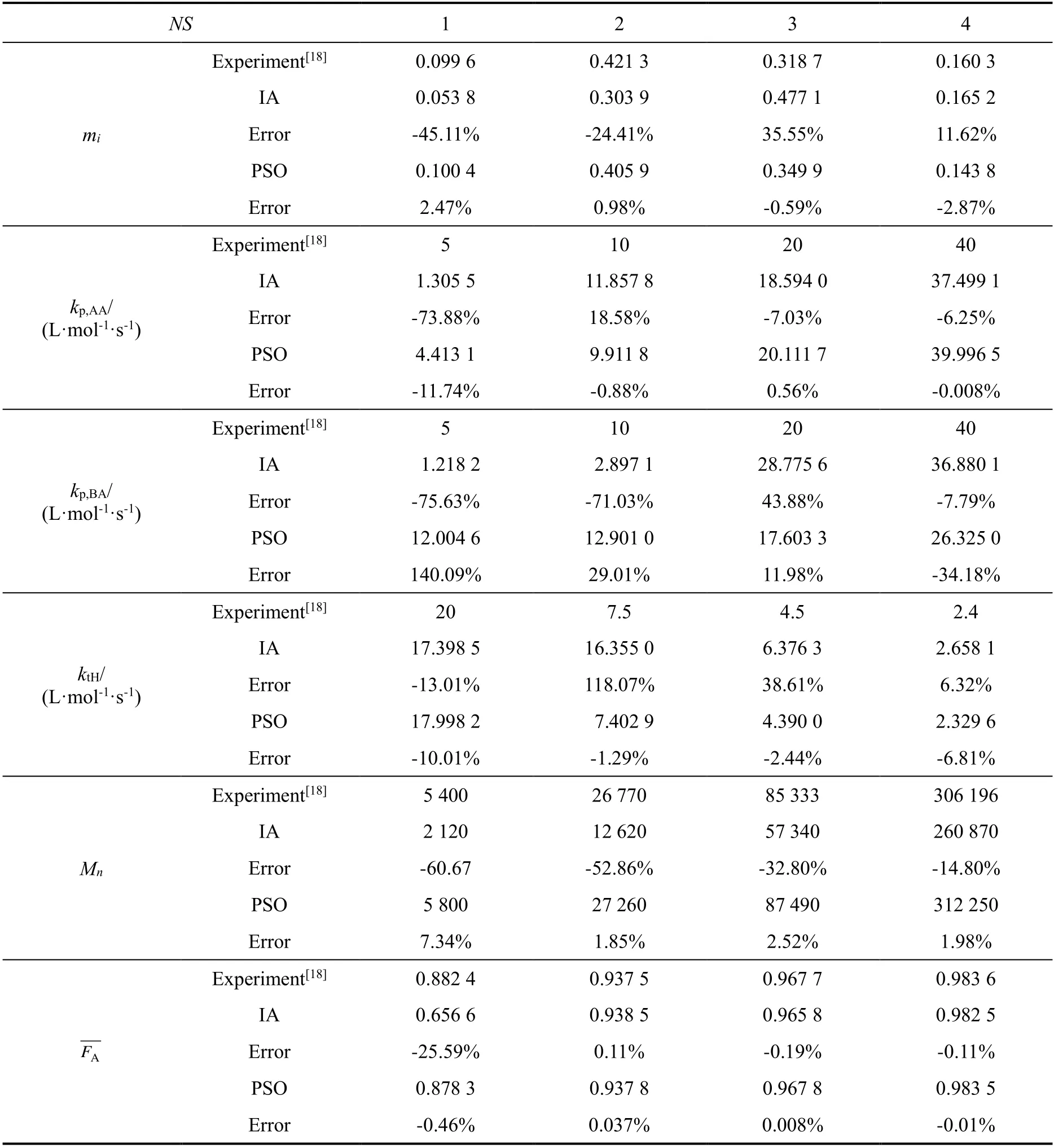
表4 以MWD-CCD为目标的共聚反应动力学参数估计结果Table 4 Estimated kinetics parameters of copolymerization with target MWD-CCD

采用IA算法与PSO算法对以MWD，MWD-SCB和MWD-CCD为目标的动力学参数估计计算所需的时间见表5。由表5可知，PSO算法的求解时间至少比IA算法快一倍以上，显示了该算法在动力学参数估计中的优势。

表5 IA算法与PSO算法的求解时间对比Table 5 Comparison of the computation time between IA and PSO

4 结 论

基于烯烃聚合反应动力学机理，建立了烯烃聚合过程多活性位Ziegler-Natta催化剂制备聚烯烃微观链结构的MWD，SCB和CCD预测模型。并以上述三种链结构分布曲线为优化目标、以催化剂各活性中心所产生聚合物的质量分数、链增长速率常数、链转移速率常数、竞聚率等聚合反应动力学参数为决策变量，采用IA算法和PSO算法分别进行了优化求解。两种算法均实现以MWD为目标的均聚反应动力学参数的估计，其中PSO算法的估计结果与实际数据更吻合。直接以模型预测的MWD-SCB、MWD-CCD和实际数据的误差和最小为目标，PSO可以准确实现去卷积分析并估计出共聚反应动力学参数，预测精度明显优于IA算法，且求解速度比IA算法快。