汽车门锁锁止机构棘轮棘爪磨损寿命可靠性研究

钟传磊，杭鲁滨，王 炎，黄晓波，曲志洋，吴柏锐

(上海工程技术大学 机械与汽车工程学院, 上海 201620)

汽车门锁是汽车的重要配件，其操作性、寿命和寿命可靠性直接关系到汽车的使用和安全等问题[1]。在闭锁和解锁过程中，棘爪与棘轮、棘轮与卡板、棘爪与缓冲块相接触，经过多次开闭锁后，棘轮棘爪都会产生一定的形变和磨损，而微小形变将会改变棘轮棘爪的啮合状态和接触应力，对门锁机构寿命和磨损寿命可靠度都产生影响。由于其磨损过程存在诸如载荷变化、温度变化等不可预测因素，寿命可靠度难以从理论分析给出确定值。

李春风[2]28,[3]以失效树进行了汽车门锁可靠性分析，得出了汽车门锁主要失效形式是棘轮棘爪磨损；运用ANSYS软件对汽车门锁开锁和解锁2种工况下的棘轮棘爪等机构进行了有限元分析，得到了其在不同工况下的应力和应变值，并提出了改进方案。冯元生等[4]对机构磨损可靠分析作了较深入的研究，以磨损量与时间的关系建立了磨损可靠性分析的基础模型，为便于建立显式功能函数表达式的机构系统可靠性提供了参考。

针对功能函数难以显式表达的复杂机械系统，特别是具有高次非线性特征系统，蒙特卡罗法成为解决该问题的常用方法之一，可用于磨损失效概率计算[5-7]。

机械构件磨损过程存在诸如载荷分布不均、温度变化和载荷变化等不可预测因素并具有随机性[8]，难以从理论分析给出确定值。故需通过引入概率分布统计，以磨损寿命可靠性描述构件实际使用寿命是可行方法之一。文献[9-11]提出了新的磨损数学模型以及可靠度估计方法，对于更精准地预测磨损寿命具有重要意义。

课题组通过分析所研制汽车门锁棘轮棘爪机构不同工况下的受力情况，基于Achard粘着磨损模型，推导开闭锁过程中棘轮棘爪磨损深度；以棘轮棘爪有效啮合距离作为判断指标，利用蒙特卡罗法进行有效啮合距离数值求解；导出对应磨损寿命可靠度，构造其与寿命的关联函数。该方法为汽车门锁棘轮棘爪实际使用寿命提供参考。

1 汽车门锁棘轮棘爪工况及磨损深度

汽车门锁作为车门系统内部一个复杂机械系统，可分为操动模块与执行模块，如图1所示。

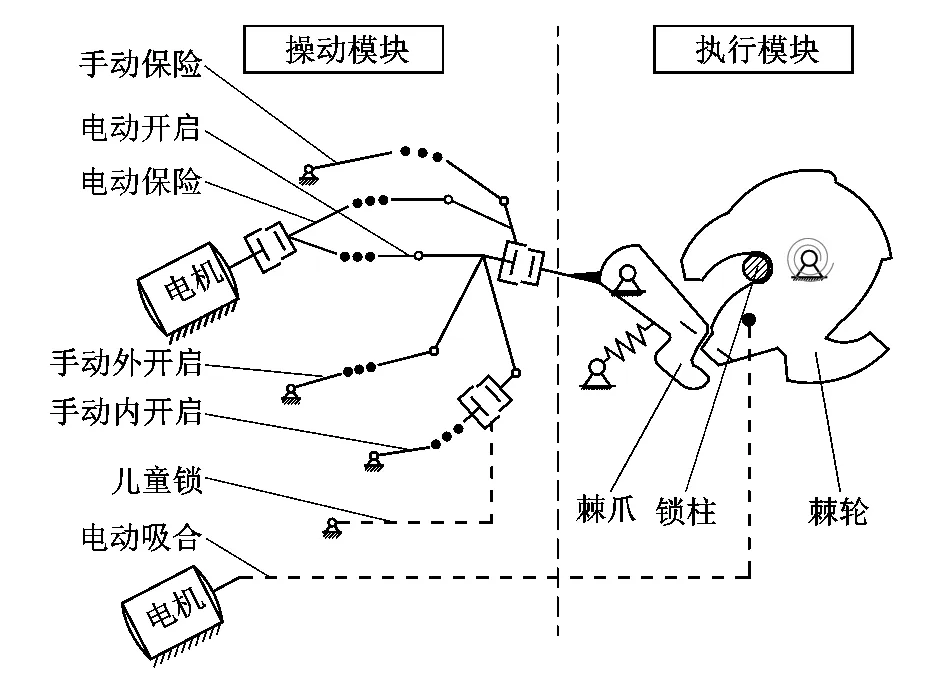
图1 汽车门锁多支链机构示意图

操动模块由多条刚柔耦合机构支链构成，其多条支链可实现汽车门锁不同功能需求；电动开启支链与电动保险支链可直接驱动执行模块并与其他支链兼容；执行模块主要由锁止机构棘轮棘爪和复位弹簧构成，是实现车门锁止及解锁的关键部分，其在闭锁工况与电动开启工况中由于受到较大接触力，啮合面会产生磨损。

棘轮棘爪磨损是新型汽车门锁的主要失效形式，其可靠性直接关乎到汽车门锁的寿命及功能。

汽车门锁在闭锁过程中一般设有全锁止与半锁止功能[2]6，决定了汽车门锁启闭过程棘轮、棘爪的磨损次数：汽车门锁在闭锁过程中，棘爪锁止啮合处经历2次磨损，棘轮锁止啮合处经历1次磨损；在电动开启过程中，棘轮棘爪啮合位置均为1次磨损。其具体解闭锁磨损过程如图2所示，其中M1和M2分别是棘轮与棘爪轴心处复位扭簧提供的复位力矩，Fs是锁体闭锁状态下所承受的密封反力。

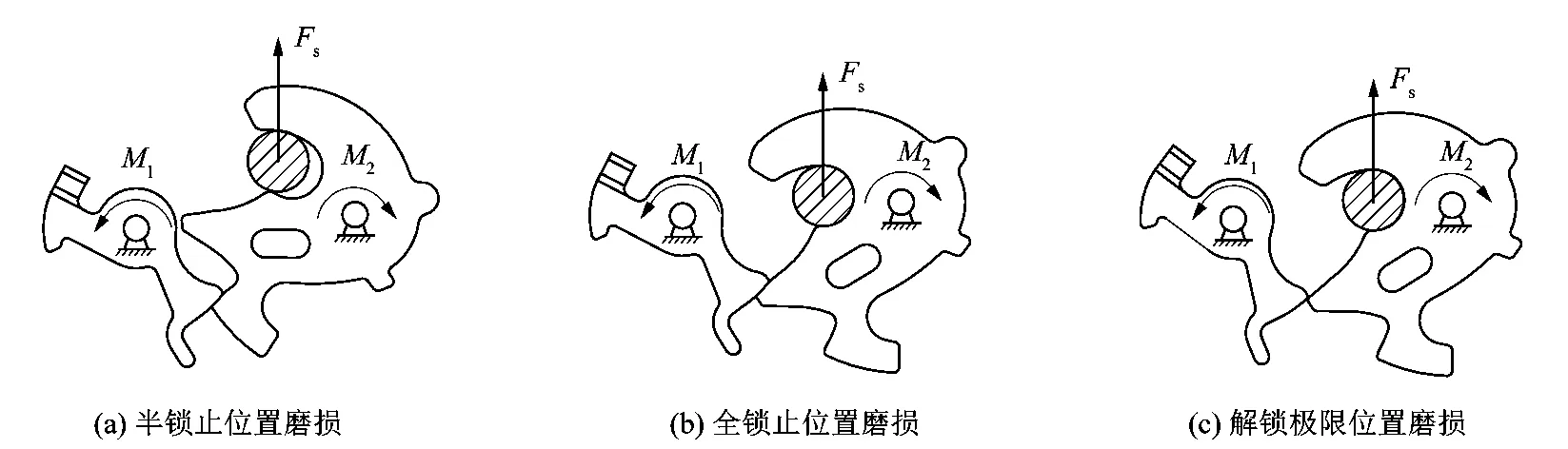
图2 汽车门锁开闭锁过程中棘轮棘爪磨损过程

汽车门锁棘轮棘爪在开闭锁过程经历多次磨损，棘轮棘爪闭锁与解锁工况下的接触力、磨损量和磨损深度是确定有效啮合距离及寿命可靠性的重要参数。

1.1 汽车门锁闭锁过程棘轮棘爪接触力

在汽车门锁闭锁过程中，分析半锁止位置对汽车门锁棘轮棘爪闭锁过程受力状况，如图3所示。

图3 汽车门锁棘轮棘爪半锁止位置受力分析

图3中：棘爪复位扭簧作用力矩为M1;啮合点处棘轮对棘爪的法向作用力为F1,摩擦力为f1；棘轮复位扭簧作用力矩为M2;接触点处棘爪对棘轮法向作用力F2,摩擦力为f2；锁柱密封力Fs。

棘爪、棘轮此接触状态瞬间的力矩静平衡方程为：

(1)

式中：F1，F2为一对作用力和反作用力；且f1=f2=μF1=μF2,其中摩擦因数μ=0.1。

由式(1)可求得半锁位置下，棘轮棘爪法向接触力F1=F2=122.92 N。

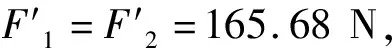
1.2 汽车门锁解锁过程棘轮棘爪接触力

汽车门锁解锁过程中，刚柔耦合机构电动开启支链驱动棘轮棘爪动作，实现汽车门锁解锁。此过程中，电动开启支链对棘爪施加的开启力矩受复位扭簧旋转角度、开启支链压力角、动力效率以及棘轮棘爪不规则外形轮廓的多因素影响，整个电动开启过程机构动力学难以解析求解，棘轮棘爪的接触力需由仿真求解。

某型包含电动开启支链与电动保险支链的汽车门锁[12]仿真模型如图4所示，其电动开启支链控制棘轮棘爪动作，实现汽车门锁电动开启功能。

图4 某型汽车门锁仿真模型

基于表1扭簧参数刚度和预载荷等参数，可进行该型汽车门锁电动解锁动力仿真。

表1 某型汽车门锁内部扭簧参数设置

电动解锁过程，棘轮棘爪接触力仿真结果如图5所示，棘轮棘爪啮合初期，接触力在150 N附近区域波动，随着棘轮棘爪有效啮合长度逐渐减少，其接触力波动愈发剧烈，会在构件末端造成更多磨损。

图5 解锁过程中棘轮棘爪接触力变化曲线

1.3 汽车门锁棘轮棘爪磨损量及深度计算

根据Achard粘着磨损体积计算公式[13]，可得棘轮棘爪磨损量Wv：

Wv=KFS/H。

(2)

式中：F为棘轮棘爪间的法向接触力；S为棘轮棘爪间的相对滑移距离；H为布氏硬度；K为磨损系数，2者与棘轮棘爪的材料有关，根据现有棘轮棘爪材料，取K=1.5×10-5N/mm2,H=165 N/mm2。

基于汽车门锁解锁过程棘轮棘爪接触力仿真分析可知，棘轮棘爪啮合末端附近的微距离元VL受力大且波动剧烈，磨损严重，其平均磨损深度可表示为：

(3)

式中：b为棘爪啮合面的厚度，取5 mm。

同理可得，汽车门锁闭锁后，棘轮棘爪的平均磨损深度为：

(4)

2 汽车门锁棘轮棘爪磨损可靠性分析

汽车门锁棘轮棘爪磨损过程存在诸如载荷变化及温度变化等不可预测因素，寿命可靠度难以从理论分析给出确定值。为简化棘轮棘爪啮合磨损数学模型以计算磨损寿命可靠性，提出以下假设：

1)棘爪受损后的锁止位置与受磨前位置保持平行，且棘轮在复位弹簧作用下，受磨损后新表面重新与棘爪啮合，即啮合表面基本形状不变。

2)假设棘爪磨损主要发生在闭锁过程中，棘轮磨损主要发生在解锁过程中。

3)假设棘轮棘爪处于正常的磨损阶段，其磨损深度与磨损次数成正比。

4)棘轮棘爪开闭锁过程中，磨损深度符合正态分布。

基于以上假设，将棘轮棘爪磨损量分析转化为对磨损前后啮合曲线变化的研究，并设立判断准则，利用蒙特卡罗法[14]求解计算磨损寿命可靠度，建立棘轮棘爪磨损寿命可靠度函数。

2.1 汽车门锁棘轮棘爪可靠性分析方法

对机械零件进行可靠性分析和评估，需模拟实际使用环境，进行大量试验数据来评估零件的可靠性。该方法经济性低、时间成本大且具有一定的技术难度。

为研究棘轮棘爪磨损寿命可靠性，课题组基于Achard粘着磨损公式，计算棘轮棘爪磨损深度；以正态分布模拟生成磨损深度，分析磨损前后棘轮棘爪啮合处曲线方程变化；选择有效啮合长度为判断准则建立磨损寿命可靠度数学模型，其具体流程如图6所示。

图6 建立磨损寿命可靠度数学模型流程

2.2 汽车门锁棘轮棘爪磨损寿命可靠度计算

以棘爪的旋转中心O点为原点，建立直角坐标系如图7所示，其有效啮合距离由虚线表示。

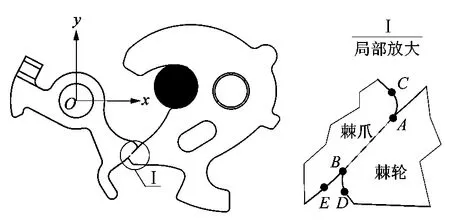
图7 棘轮棘爪磨损模型坐标系建立

从图7所示的局部放大图中可知，上极限啮合点A和下极限啮合点B之间的距离|AB|为有效啮合距离。

棘轮棘爪每次开闭锁磨损后，受扭簧力约束作用回到初始位置，圆弧CA圆心坐标保持不变；啮合线段AB磨损点沿垂直各自平面向里的方向进行磨损。设每次开闭棘爪磨损深度为Δy1；棘轮啮磨损深度为Δy2。

棘轮棘爪间的有效啮合长度|AB|是其原始尺寸和磨损量的复杂随机函数，难以精确求出其解析表达式。

经过n次开闭锁磨损后，A点坐标(xA,yA)满足棘爪边界圆弧CA和棘爪边界直线AE曲线方程，即通过联立方程(5)进行求解：

(5)

式中：棘爪边界圆弧CA圆心坐标(15.34,-12.18)，半径0.8 mm；棘轮边界圆弧BD圆心坐标(15.13,-15.30),半径1.3 mm；A点初始坐标(15.97,-12.67)，B点初始坐标(13.91,-14.88)，E点初始坐标(13.31，-15.44)。

同理，B点坐标(xB,yB)可通过联立棘轮边界圆弧BD和棘轮边界直线BE曲线方程进行求解。

(6)

由上得出啮合极限点A与B，可求出有效啮合距离|AB|：

(7)

为保证汽车门锁锁体有足够强度，有效啮合距离需大于2.0 mm[15]。考虑制造误差、安装误差和安全系数等因素[16]，课题组取有效啮合距离|AB|<2.1 mm作为门锁机构的磨损失效判断准则；棘轮棘爪磨损寿命可靠度可由有效啮合距离|AB|求解。

根据式(7)计算出一系列|AB|值，从而估算棘轮棘爪在不同开闭次数下的磨损寿命可靠度：

(8)

式中：n1为|AB|符合有效啮合长度的数据点数，n2为总模拟数据点数。

2.3 汽车门锁棘轮棘爪寿命可靠度关联分析

将门锁开关次数n依次取1.0×105,1.1×105,1.2×105代入到上述方法中，利用MATLAB编程计算求解有效啮合长度分别为：2.370 0，2.328 6和2.277 2 mm。此时，门锁机构磨损寿命可靠度均为100%，不会失效。

如表2所示，列出了开闭次数n取120 000至170 000时，以5 000为步长模拟计算的结果。

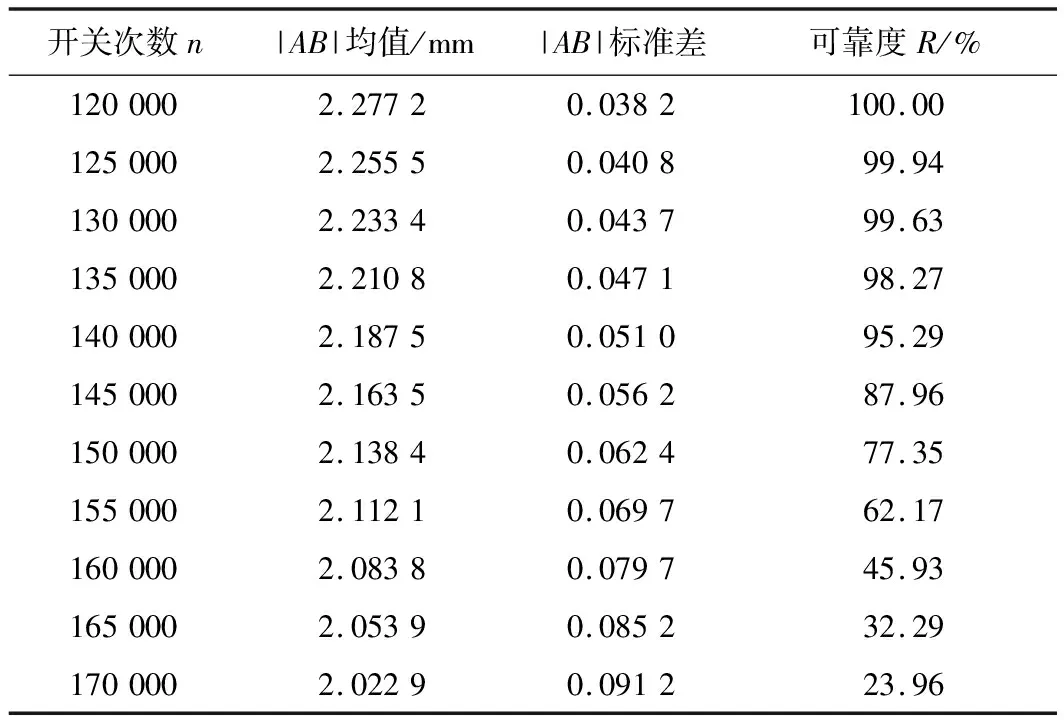
表2 棘轮棘爪磨损寿命可靠度

根据表2的计算结果,用最小二乘法拟合出棘轮棘爪机构的磨损寿命可靠度函数：

R=6.289×10-17n4-3.587×10-11n3+7.591×10-6n2-0.707 4n+2.463×104。

(9)

其拟合曲线如图8所示，不但可以预测磨损寿命的可靠度，还可根据可靠度目标估算棘轮棘爪使用寿命，为新型汽车门锁产品质量提升及行驶安全性提供参考基础。

图8 棘轮棘爪磨损寿命与寿命可靠度曲线

3 结论

课题组通过分析汽车门锁棘轮棘爪机构不同工况下受力情况，基于Achard粘着磨损模型，利用蒙特卡罗法进行有效啮合距离数值求解，构造磨损寿命可靠度函数，主要工作及创新点如下：

1)根据开闭锁过程中棘轮和棘爪半锁、全锁关键接触位置的受力分析和仿真，得出了车门棘轮和棘爪锁止机构平均接触力。

2)基于汽车门锁棘轮棘爪半锁、全锁工况啮合接触力，结合零件磨损Achard理论，分别计算了门锁、棘轮棘爪的磨损深度，并分别代入对应啮合面曲线方程，计算棘轮棘爪有效啮合距离。

3)以有效啮合距离作为判定指标，通过正态分布生成磨损数据，利用蒙特卡罗法求得棘轮棘爪磨损寿命可靠度并求得使用寿命与磨损寿命可靠度关联函数。通过对标门锁实际使用寿命，本方法可大大节省磨损试验的时间成本。