基于麻雀算法的Web服务组合
杨宏伟,薛富城,李 莉
(长春理工大学 计算机学院,吉林 长春 130022)
0 引 言
目前解决Web服务组合问题的方法可以分为两类:一类是根据服务质量属性值(QoS)通过智能算法进行寻优求解模型[1];另一种是通过Petri网工具进行建模求解[2]。如果单纯采用Petri对服务组合进行求解,当服务数量过于庞大时,复杂度过高;如果单纯采用智能算法对QoS模型进行求解时,智能算法大都会在接近最优值时陷入局部最优值并且不能具体表达出各组合服务间的逻辑关系。
在本文中,我们将介绍一种基于Petri网的Web服务组合模型,并通过麻雀算法对模型进行求解,该方法对解决Web服务组合问题有良好的效率和准确度,并且在面对复杂问题时能更清晰表现出各组合服务之间的逻辑关系。本文的主要贡献如下:
(1)为了清楚地描述服务之间约束关系和执行逻辑,本文提出了基于Petri的服务组合模型对组合过程进行建模,将服务组合所有逻辑关系在Petri网进行映射,对Petri网的结构和行为进行分析验证,可对服务组合的可行性、有效性、逻辑合法性进行验证以及冲突解决,获得服务质量更优的组合序列;
(2)如果单纯采用Petri对服务组合进行求解,当服务数量过于庞大时,复杂度过高,因此在Petri网模型基础上,本文提出了麻雀(SSA)算法的服务组合模型,采用自适应步长调节的方法,避免了算法陷入局部收敛导致局部最优的结果。考虑服务质量可靠性、可用性、执行时间、性能和成功率对服务组合进行多目标优化,通过Petri网对服务组合的合法性进行验证,得出最优服务组合序列。
1 相关工作
根据服务质量属性(QoS)的方法已经受到广泛的研究关注。解决大规模服务组合问题时,改进的遗传算法(GA)[3-5]、改进的蚁群优化算法(ACO)[6-8]和改进的粒子群优化算法[9,10]可以高效解决服务组合问题。但是这些算法都是将多目标问题转化为单目标问题,会出现局部最优值情况。文献[11]提出了一种多目标蜂群算法的Web服务组合优化方法,文献[12]中的作者使用改进的万有引力搜索算法解决问题,文献[13]提出了一种融合遗传聚类的可靠Web服务组合优化方法。文献[14]对基于QoS的Web服务组合多目标算法进行了比较分析。huo等[15]提出了一种Eliteguided多目标人工蜂群算法有效解决了Web服务组合问题。一种改进的遗传算法(CGA)[16]使用一种真正的编码方法来解决基于QoS的服务选择问题,避免了算法中长染色体的负面影响。
Petri网建模和模拟的能力非常强大,能够直观地表示出系统中的关系,可以通过网的运行对系统的可达性、活性、有界性进行分析。所以目前很多学者使用Petri网理论来解决Web服务组合问题。Groefsema H等[17]使用有色Petri网将服务组合映射到Kripke结构。Entezari-Maleki等[18]提出了一种基于定时彩色Petri网(TCPN)的模型,用于评估多云环境中的服务组合,同时最大程度地减少服务于组合服务请求的云数量。Sha等[19]为了提高服务发现的准确性和效率,提出了一种基于Petri网的面向用户需求的Web服务发现方法。
对于现有的研究,服务组合问题已取得了一定的成果,但大部分的研究都很少考虑到服务QoS属性计算方式与组合顺序有密切关系,较少地考虑了基于QoS属性评估的同时对服务组合的合法性、可行性以及服务执行的逻辑合理性的分析验证。因此本文针对这些问题在基于Petri网的服务组合方法基础上结合改进的麻雀算法对服务组合进行合法性判断,并通过逻辑顺序对服务组合的QoS进行计算,选择出最优的服务组合序列。
2 基于Petri网的服务组合模型
Petri网[20]的概念是德国科学家Carl Adam提出的,用于描述系统结构及执行逻辑的一种网状模型。云环境中存在很多应用,通过这些应用能够高效率地完成用户所提出的请求。所以本文以其中某服务作为例子,用户发出请求R,首先将其分解为多个子任务R=(Task1,Task2,…,Taskn)完成,其中每个子任务Taski,(i=1,2,…n)完成某一特定功能。任务R由该子任务集合按照一定业务逻辑完成任务,在执行每个子任务的过程中,通过服务发现,每个子任务Taski,(i=1,2,…n)都可由多个候选原子服务来完成,假设子任务Task有m个候选原子服务表示为Si=(si1,si2,…,sim),在这些候选服务集合中,通过对比服务非功能属性选择一个综合性能最优的Web服务Sik,(k=1,2,…,m)来执行子任务Task。当所有的子任务都选择了对应的原子服务,则可进行服务组合。通过服务选择,计算每个组合服务的QoS值,最终选择出性能最优的服务组合方案,最后的组合方案按照请求的一定逻辑顺序执行。为了完成用户的请求,需通过服务组合将每个任务的相关特定功能的原子服务集合进行集成。由于不同服务之间存在着执行逻辑关系,为了能够了解服务之间的相互关系,本文采用Petri网进行建模对网系统进行动态分析和验证。
定义1 定义一个原子服务,其可表示为四元组cs={s_id,s_function,s_type,s_status,s_constr}。其中s_id表示服务的标识,s_function表示服务具有的执行功能,s_type表示服务类型,s_status表示该服务状态,s_constr表示服务之间约束关系或者评价指标值。
定义2 定义一个服务组合优化Petri网(service composition petri net,SCPN),其由十一元组P={P,T,E,L,I,O,F,Eth,Lth,S,Mcs} 组成,其中当且仅当:
(1)P={p1,p2,…,pm} 表示库所的有限集合,其中,pi,(i=1,2,…,m)表示候选原子服务集合的第i个原子服务;
(2)T={t1,t2,…,tn},(n>0)表示变迁的有限集合,其中P∩T=∅,P∪T≠∅;
(3)E={e1,e2,…,em},(m>0)表示原子服务响应时间评估值的有限集合,表现出服务组合中原子服务的执行效率;
(4)L={l1,l2,…,lm},(m>0)表示原子服务失效频率的有限集合;


(7)F⊆(P×T)∪(P×T)表示SCPN网有向弧的有限集合;
(8)Eth={eth_1,eth_2,…,eth_m} 表示服务响应时间临界值的有限集合;
(9)Lth={lth_1,lth_2,…,lth_m} 表示服务失效频率临界值的有限集合;

(11)dom(F)∪cod(F)=P∪T;

3 基于麻雀搜索算法的Web服务组合
3.1 标准的麻雀搜索算法
麻雀搜索算法(sparrow search algortihm,SSA)是一种受到麻雀觅食和被捕食预警的新的群体智能算法,它的搜索精度和收敛速度等比其它群体智能算法更为优秀,并且其参数较少,稳定性高[21]。麻雀算法可根据其觅食的过程表示为发现者-加入者模型,在此基础模型中还加入预警报告机制。
在SSA中,模拟麻雀觅食过程获得优化问题的解。由n只麻雀组成的种群可表示为如下形式
(1)
其中,d为问题维数,n是麻雀的数量,所有麻雀的适应度值如下
(2)
其中,f表示适应度值。
发现者一般占到种群的10%~20%,位置更新公式如下

(3)
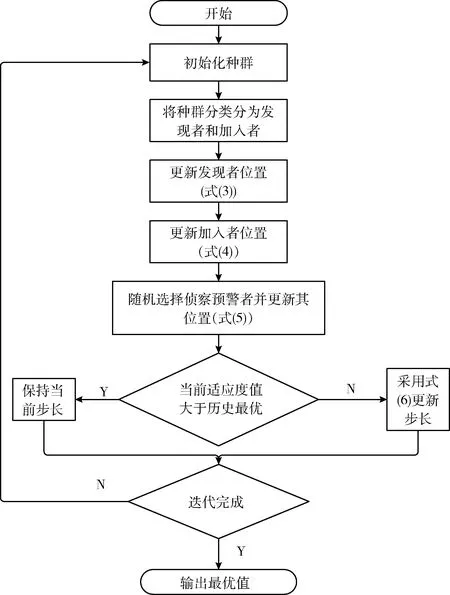
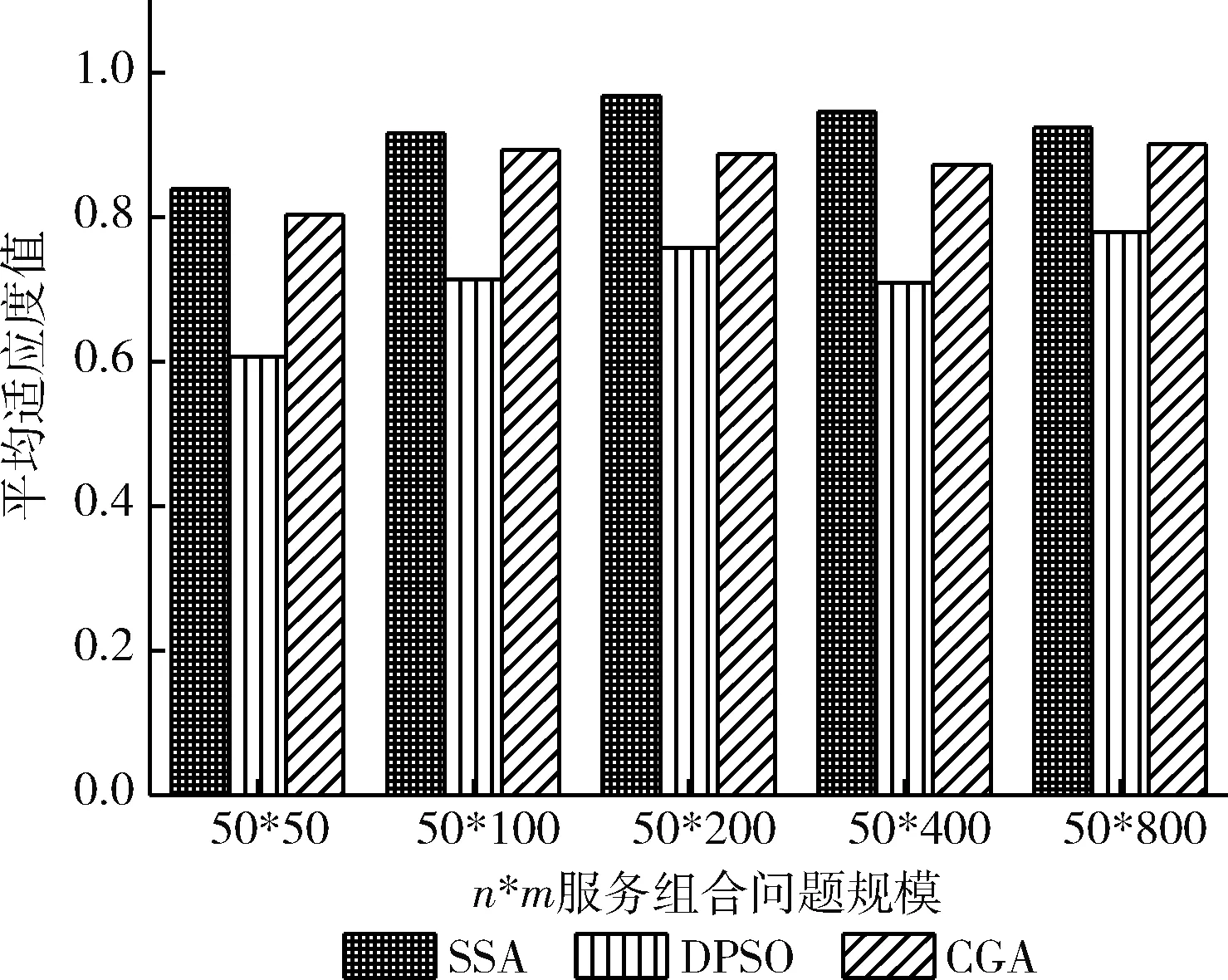
其中,t代表当前迭代次数;α为0到1之间取值的随机数;T为最大的迭代次数;L表示大小为1*d的单位阵;Q是服从标准正态分布的随机数;R0∈[0,1]和YJ∈[0.5,1]分别表示预警值和安全值。当R0 除了发现者,其余的麻雀都为加入者,并根据下式进行位置更新 (4) 侦察预警麻雀占到种群的10%~20%,其位置更新公式如下 (5) 其中,β表示步长参数,取值为一个正态分布的随机数,并且均值为0,方差为1;e是无限接近于0的一个常数;K的值在[-1,1]之间随机确定,表示麻雀飞行的方向;fi表示第i只麻雀的适应度值,fg是当前种群最佳适应度值;fw表示当前种群最低适应度值。预警麻雀的位置更新可分为两种情况:①当fi≠fg时,表示当前麻雀的位置偏离群体,容易被捕食者猎食,应当发出警告,此时算法容易陷入局部最优,可根据公式进行调整;②当fi=fg时,表明当前麻雀的位置在群体之中,可以通过预警,及时调整觅食的搜索路线,避免被捕食者猎食。 步长因子是控制算法收敛的关键。如果步长衰减过快,麻雀搜索算法可能无法获取最优解;反之,麻雀算法可能陷入局部最优解。为了使算法获得更好的优化能力,本研究提出了一种动态改变步长因子的改进方法。在麻雀算法前期,采用较大的步长控制因子来扩大解空间中的整体搜索范围并加快搜索速度;在优化的后期,解空间趋于稳定,此时应该提高解的精度,减小步长控制因子。基于以上的考虑,本研究对麻雀搜索算法的步长控制因子β进行改进 β=α-0.2·((i+1)/5·Gmax)+0.5),fi (6) β=α,fi≥fpbest (7) 其中,Gmax为最大迭代次数,fi是当前适应度值,fpbest是历史最佳适应度值,i是当前迭代次数,α是默认步长因子,β是当前步长。 算法流程如图1所示。 图1 自适应步长麻雀算法流程 服务组合的评价标准主要是通过服务各个属性指标对服务组合性能进行综合评价。根据Petri网SCPN的变迁规则以及各个指标计算方法来确定麻雀搜索算法的适应度函数。但在确定适应度函数之前,由于不同的指标其标准不同,需对各个指标进行标准化。Web服务QoS的多个属性对QoS综合值的正负影响不同,因此提出了两种服务属性:正服务属性和负服务属性。 正服务属性:针对本文所考虑的QoS属性,其中可用性、可靠性、性能以及成功率都属于正服务属性。对于用户而言,Web服务的可靠性越高,其QoS值越高,更值得用户信任。 负服务属性:负服务属性表示属性的取值与服务质量成反比,比如执行时间,执行时间越长,用户的体验度就会越差,服务质量越低。 为了能够统一标准,便于计算,对QoS各个属性进行标准化处理,将其值转换至区间[0,1],其QoS值越大服务质量就越高,标准化处理后的服务质量QoS的二维矩阵表示如式(8)所示 (8) 其中,Qt表示标准化后的矩阵,矩阵的行代表各种QoS属性值,矩阵的列代表各个属性的值。矩阵可以适当扩展。每当添加属性时,都应在矩阵中添加一列。 QoS属性标准化公式如下 (9) (10) 通过对各个服务质量属性进行了标准化后,可得到适应度函数公式如式(11)所示 (11) 对于服务组合的问题中,采用二进制编码会使得问题更加复杂,假设有R个服务需要进行组合,每个服务都具有K个候选原子服务,采用二进制编码的解将有R×K个二进制位,表示成SV={r11,r12,…,r1k;r21,r22,…,r2k;…;rr1,rr2…,rrk}。其解空间过于庞大,对于系统来说在计算的过程中太浪费内存和时间。因此本文采用十进制进行编码大大缩减了解空间,具体编码方式如下: 假设Web请求R需要W个子任务(Task1,Task2,…,Taskw)一起完成,其每个子任务都需要一个服务完成,其每个服务都有一个候选服务集合Si=(si1,si2,…,sim),(i=1,2,…,w),则编码方式可表示成SV={r1,r2,…,rk…,rw},由W个整数组成的解空间,其中,rk∈{1,2,…,m},m∈N*,每个服务的候选服务数量可能不同,因此m的取值也可能不同。 为了验证本文提出的Petri网模型的可行性,本文采用了Petri的可达标识图分析方法[21]对Petri网TBPN进行动态性能分析,对于系统服务执行逻辑进行死锁判断。为了能够获得全局最优的服务组合,本文在Petri网SCPN描述多约束的基础上,结合本文提出的SSA算法有效避免了出现复杂度高或者随机性大的问题。本研究的作者使用QWS真实数据集对顺序结构进行了大量实验[22]。QWS数据集是由Guelph大学的Eyhab Al-Masri教授收集的Web服务数据集。QWS中的所有数据集都是从各个服务网站收集的真实数据集。该数据集包含2507个实际服务和9个QoS值。实验环境如下:Intel(R)Core(TM)i5-8300H CPU@2.30 GHz 2.30 GHz,16 GB ddr4 2666 MHz memory,64 bit Windows 10 OS,and MATLAB R2015b。 通过可达标识图对SCPN网络可达状态进行分析。该实例的初始标识状态为M0={1,0,0,0,0,0,0,0,0},其可达集见表1,其中所有状态标识供9种,模型标识为PBTPN={p1,p2,p3,p4,p5,p6,p7,p8,p9},其每一行代表一个标识。 表1 SCPN网可达集合 网络可达状态分析结果如图2所示。 图2 可达状态分析结果 对BTPN的可达状态标识图进行分析,以状态序列(M0,M1,M4,M6,M7,M8)为例进行分析,其结果如下。其中,Stat表示状态,Tran表示变迁。 (1)M0={1,0,0,0,0,0,0,0,0},Stat={M0},Tran=∅; (2)M1={0,1,0,0,0,0,1,0,0},Stat={M0,M1},Tran={t1}; (3)M4={0,0,0,1,0,0,0,0,0},Stat={M0,M1,M4},Trasition={t1,t4}; (4)M6={0,0,0,0,0,0,1,0,0},Status={M0,M1,M4,M6},Trasition={t1,t4,t6}; (5)M7={0,0,0,0,0,0,0,1,0},Status={M0,M1,M4,M6,M7},Trasition={t1,t4,t6,t7}; (6)M8={0,0,0,0,0,0,0,0,1},Status={M0,M1,M4,M6,M7,M8},Trasition={t1,t4,t6,t7,t10}。 从运行结果可知,从系统最初状态M0通过变迁序列总能到达系统结束状态M8,因此网系统不存在死锁,所有的状态都包含所有库所和变迁,因此该网系统具有活性和全覆盖性,服务组合之间逻辑结构具有正确性以及有效性。 本节实验用来验证不同用户偏好对服务组合评估的影响,用来对比本文提出的方法在服务组合优化领域的有效性,排除用户偏好对算法进行组合服务选择的干扰性。本文将提出的SSA算法与DPSO算法和文献[16]中的CGA算法进行对比。本文选取文献[23]给出20组的不同的用户偏好进行了实验对比,实验参数为:选取可用性、吞吐量、响应时间和可靠性4种QoS属性,迭代次数500次,子任务数为10,候选服务集的规模为100个,用户偏好的具体值见表2。 表2 用户体验 具体实验结果见表3,根据组合服务的目标函数计算方式,在不同的用户偏好下,使用改进的SSA算法寻找的组合服务适应度值高于其它算法,本节实验可以排除用户偏好对于SSA算法进行服务组合的影响。 表3 每个用户体验的适应度值 本节将对所提出算法解决服务组合问题的有效性进行分析。对比使用SSA、DPSO和CGA这3种算法计算适应度函数100次求得的适应度值的平均值,适应度值大的算法有效性高。选取服务规模为n*m,n为服务请求数,m为候选服务数。分别取n为10,20,50;分别选取m为50,100,200,400,800。迭代次数设置为100。实验结果如图3~图5所示。 图3 n=10时3种算法的平均适应度值 图4 n=20时3种算法的平均适应度值 图5 n=50时3种算法的平均适应度值 从实验结果图中得出,无论服务组合规模如何增长,SSA始终保持着比另外两种算法高的平均适应度值,说明SSA算法解决服务组合问题的有效性;当问题维度升高时,在n达到50时,SSA仍然有着比另外两种算法高的平均适应度值,表明SSA算法在面对高维度问题时的有效性和高精确性。 智能算法的重要性能指标之一就是其收敛性[24]。算法的收敛是指经过多步迭代之后得出的数值不应该无限增大, 而是趋于某个数值,不能收敛的算法是没有使用价值的。本节将分析实验结果,重点讨论SSA算法的收敛性。 为了更清晰表现算法的收敛性,本节将迭代次数设为100,服务规模n*m设为:10*10,20*20,50*50;选取不同规模服务组合50次实验后的平均适应度值。实验结果如图6~图8所示。 图6 10*10服务规模 图7 20*20服务规模 图8 50*50服务规模 从图6~图8中可以看出,当服务规模为10*10、迭代次数为10时,SSA算法的平均适应度值已经明显高于另外两种算法;随着迭代次数的增加,SSA开始收敛,当迭代次数到达50时,SSA算法已经收敛。同理,随着服务规模的增长,SSA在迭代50代左右,同样会趋于最优值。这表明SSA算法有着良好的收敛性能。 智能算法的稳定性是在面对复杂问题时能否准确得出最优值的关键。本节为了验证SSA算法解决不同规模的Web 服务组合的稳定性,将SSA、DPSO和CGA算法在问题维度为10*10、20*20、30*30、40*40和50*50这5种情况下运行50次,记录各算法所得适应度值并计算其标准差。在同等情况下,平均适应度值标准差低的,算法稳定性强。 从图9中可以看出,SSA算法的标准差明显小于另外两种算法。随着服务规模的增长,3种算法的标准差都在增长,这是因为问题的维度在不断扩大,算法的稳定性都受到了影响。在50*50规模时,算法的标准差明显高于在10*10规模时,但SSA算法仍然低于另外两种算法,并保持在较低的水平。这表明SSA的算法稳定性良好。 图9 算法标准差 针对Web服务组合现有的模型单一、无法清楚表示出各服务组合间的逻辑关系和当问题规模变复杂时智能算法效率低下等问题,本文首先提出了基于Petri网的服务组合模型SCPN网,并对所提出的模型进行了可行性验证。然后提出了基于自适应步长调节的麻雀搜索算法对模型进行了求解。通过实验验证了所提出的SCPN网模型对解决服务组合问题的可行性,同时验证了所提出改进的SSA算法具有收敛速度快、搜索精度高、算法性能稳定和解决服务组合问题的有效性。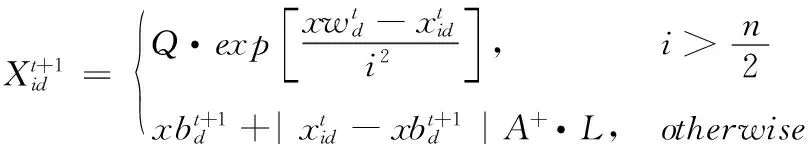
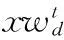
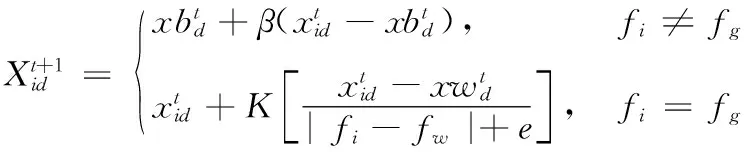
3.2 自适应步长调节的麻雀搜索算法
3.3 适应度函数设计


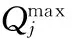

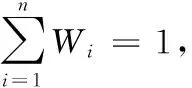
3.4 编码方式
4 实验与结果分析
4.1 实验环境
4.2 Petri网系统的服务组合验证与分析


4.3 用户偏好设置


4.4 有效性分析


4.5 收敛性



4.6 算法稳定性

5 结束语

