体育馆双层圆柱面网壳结构抗火研究

万 杰

（武汉船舶职业技术学院，湖北武汉 430050）

网壳结构由于受力性能合理、建筑造型优美、应用跨度广泛及施工快速便捷，已广泛应用于体育馆等大空间建筑结构中。但在高温作用下，结构杆件的力学性能指标会发生显著降低，建筑可能在极短的时间内发生坍塌。而且此类建筑通常人员高度密集，一旦发生火灾必然造成大量人员伤亡，因此网壳结构的抗火研究对减少结构的火灾危害、保护人员和财产安全具有非常重要的意义。

目前针对网壳结构抗火设计主要参考《建筑钢结构防火技术规范》（GB 51249-2017）[1]，通过对结构进行承载力极限状态验算来保证钢结构在设计耐火极限时间内的承载安全。耐火承载力极限状态验算又包含基于整体结构的耐火验算和基于构件的耐火验算，但针对不同的结构采用何种验算方法规范并未明确说明，如何基于整体对结构进行耐火验算也未详细叙述。

本文以某体育馆主跨双层圆柱面网壳结构为例，选用ISO834 标准升温曲线通过ANSYS 数值模拟软件分析了结构在不同温度下的力学性能，明确了双层圆柱面网壳结构耐火承载力极限状态验算方法，分析了不同支座约束条件对结构的影响。

1 有限元模型

1. 1 工程概况

双层圆柱面网壳结构以武汉某学院体育馆为工程背景。该工程为老工业厂房改造项目，结构形式为正放四角锥球壳网架。建筑物设计主结构基准期为50年，建筑设计使用年限为50年，建筑结构安全等级为二级，耐火极限不小于1小时。

网架屋面为双层压型钢板复合保温板，采用外板0.8mm 压型钢板，中间采用高级别阻燃岩棉100mm，内板0.6mm，采用镀铝锌基板。网架荷载包括：（1）上弦恒载（标准值）：0.30kN/m2（不含网架自重）；（2）上弦活载（标准值）：0.50kN/m2；（3）下弦恒载（标准值）：0.15kN/m2（不含网架自重）；（4）温度荷载。

1. 2 材料属性

钢材的密度为7850kg/m3，泊松比为0.3。弹性模量和屈服强度随温度变化很大，不同温度下参数的折减参考《建筑钢结构防火技术规范》（GB 51249-2017）[1]，如表1所示。钢材的应力—应变关系参考《Eurocode3-Design of Steel structures—Part 1-2 - General rules - Structural fire design》[2]，如图1所示。

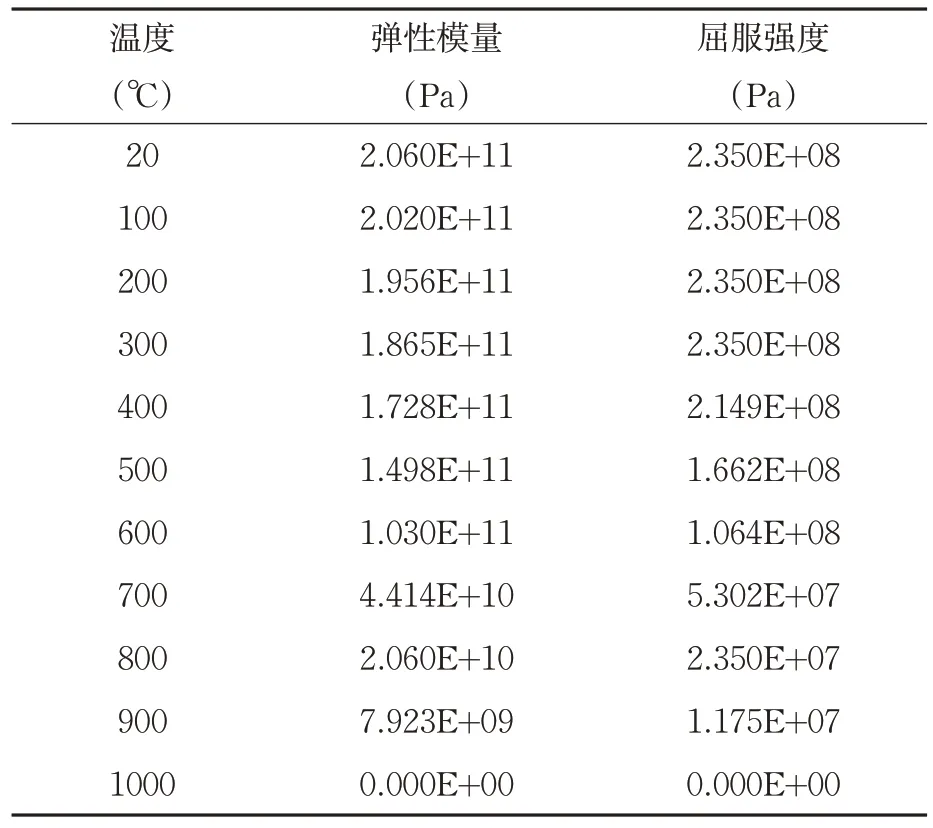
表1 不同温度下钢材弹性模量和屈服强度

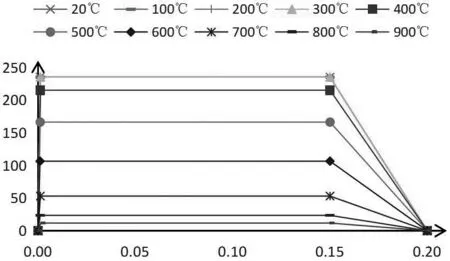
图1 钢材的应力—应变关系曲线

1. 3 有限元模型

双层圆柱面网壳结构所有杆件采用LINK180单元模拟，如图2 所示，共计998 个单元。上弦恒载、上弦活载和下弦恒载均采用等效节点荷载方式施加。即在程序中建立表面效应单元SURF154，对所有节点施加三个方向约束，再在该表面效应单元上施加各类恒载和活载，求解得到的节点反力大小即为等效荷载的值。

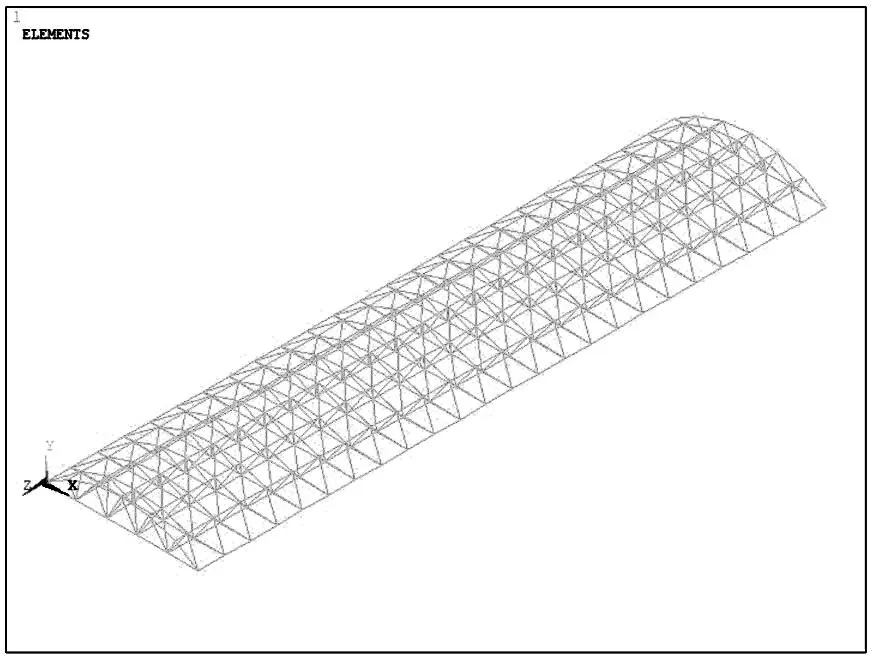
图2 有限元模型

不同的边界约束对结构的抗火能力有着显著影响[3]，因此本文考虑两种不同的理想约束条件，分析结构在火灾作用下的各种受力和变形情况。

方案一：X轴方向约束、Z轴方向约束；

方案二：X轴方向释放、Z轴方向释放；

实际火灾的发展取决于可燃物种类、数量及分布情况，而构件温度又受建筑物空间、形状及通风等情况所影响，本文采用ISO834 火灾标准升温曲线评定结构的耐火极限。在无防火保护条件下火灾中钢杆件的温度值参考《建筑钢结构防火技术规范》（GB 51249-2017）[1]计算公式，温度—时间关系曲线如图3 所示。从曲线中可以看出，前1800s杆件温度相对于环境温度有一定延迟，1800s 以后杆件温度和环境温度基本一致。

图3 温度—时间关系曲线

2 计算结果及分析

2. 1 方案一约束计算结果

在X轴和Z轴方向同时约束条件下，程序运行至900s 后计算不收敛，此时作用于结构上温度为705℃，表明结构在此温度作用下突然发生大变形而垮塌。因此程序计算不收敛时的时间可作为结构整体破坏的耐火极限时间，但需要注意排除数值计算不收敛的情况。

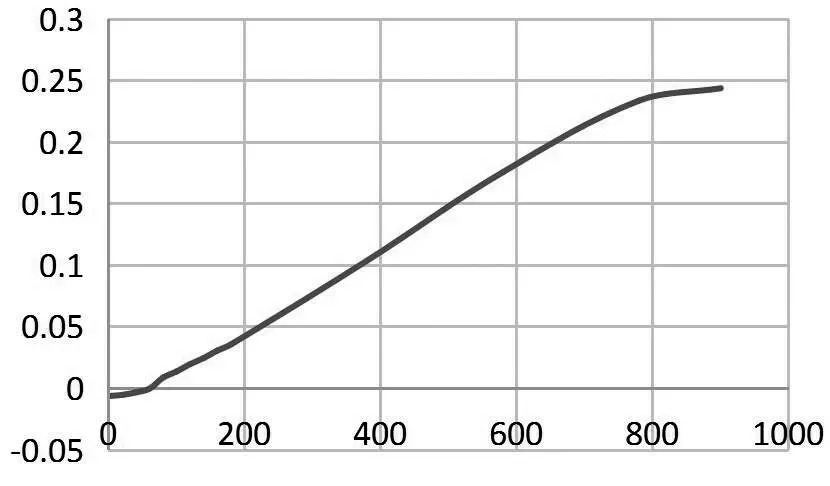
图4 结构竖向位移随时间变化曲线

在0s 时结构处于常温20℃作用下，竖向位移为-0.006m。当温度随着时间逐步升高，由于支座的约束作用，结构在拱形上弦杆的带动下位移逐渐减小。在60s 时结构竖向位移为0m，随后转为正值并逐渐变大。在大约800s 后，正向位移变化趋于平缓，说明结构开始进入塑性变形阶段。因此在在X轴和Z轴方向同时约束条件下，整体升温荷载对结构竖向位移有利。

网架结构基于构件耐火验算需进行轴心受拉杆件的强度验算和轴心受压杆件的稳定性验算，本文将各个时刻下验算未通过的受拉和受压杆件数分别统计列于图表中，如图5所示。从图中可以看出受拉杆件强度验算失效数在180s前为0根，整个过程最高时为12根，占杆件总数比例仅1.2%。而受压杆件稳定性验算失效杆件数在60s就突破零根，180s达到374根，并维持了一段时间，然后在660s继续上升最高至470根，占杆件总数比例达47.1%。

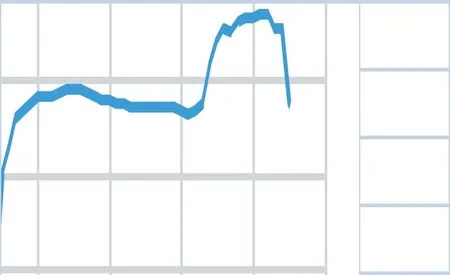
图5 验算未通过杆件数随时间变化曲线

2. 2 方案二约束计算结果

在X轴和Z轴方向同时释放情况下，程序运行至780s 后计算不收敛，此时作用于结构上温度为667℃，表明结构在此温度作用下突然发生大变形而垮塌。相比于双向约束情况，双向释放方案不收敛时间提前了120s，此指标下临界温度降低了38℃。

结构竖向位移随时间变化分为三个阶段，如图6所示。第一阶段从0s到160s，竖向位移一直维持在-0.013m 左右不变；第二阶段从160s 到640s，竖向位移随时间呈线性变化趋势；第三阶段从640s到780s，竖向位移呈指数变化趋势，最大达到-1.083m。因此在在X 轴和Z 轴方向同时释放情况下，整体升温荷载对结构竖向位移不利，可以将第二阶段结束的时间640s作为位移控制的耐火极限时间，此时临界温度为599℃。

图6 结构竖向位移随时间变化曲线

图7 验算未通过杆件数随时间变化曲线

基于构件耐火验算情况列于图表7 中。从图中可以看出，在620s 之前轴心受拉杆件的强度验算和轴心受压杆件的稳定性验算失效数都为0根。在620s后，受拉杆件的强度验算失效数为101根，受压杆件的稳定性验算失效数最大为201根。

2. 3 两种方案计算结果对比

通过以上计算结果可以看出：双向同时约束条件下，无论是计算不收敛的时间指标还是竖向位移指标都是优于双向释放情况。但由于强约束作用构件升温热膨胀产生了很大的温度内力，在较低温度时就有较多受压杆件稳定性验算失效。而失稳破坏作为脆性破坏，结构中出现一定构件失稳破坏有可能造成结构连续破坏甚至倒塌。

双向同时释放情况下，虽然计算不收敛的时间相对于双向同时约束短了120s，竖向位移指标也缩短了结构的耐火极限时间，但基于构件的耐火极限时间大大延长，和基于整体结构的耐火极限时间处于同一水平。因此为了避免局部杆件失稳影响整体结构，双层圆柱面网壳结构的支座设计应尽可能释放水平方向约束。

3 防火涂料计算

防火涂料计算模型支座约束采用X轴和Z轴方向同时释放方案，耐火极限时间根据最不利情况基于构件耐火验算情况确定为620s，此时临界温度为587℃。

项目设计耐火极限不小于1小时，因此必须采取防火措施。考虑采用膨胀型防火涂料，火灾下有防火保护钢构件的温度计算公式参考《建筑钢结构防火技术规范》（GB 51249-2017）[1]。通过取值防火保护层不同的等效热阻，得到临界温度为587℃下耐火极限时间，如表2所示。因此本双层圆柱面网壳结构的防火涂料等效热阻最小取值为0.19m2·℃/W。

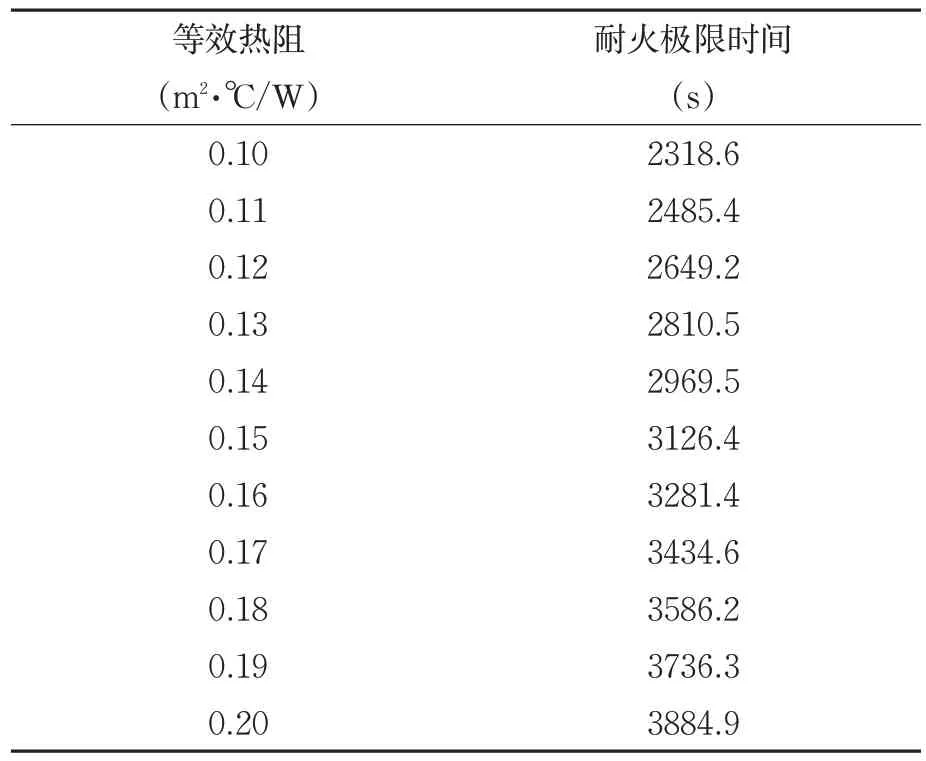
表2 不同等效热阻对应极限耐火时间表

4 结 论

本文以某学院体育馆为工程背景，分析了不同支座约束条件下双层圆柱面网壳结构抗火性能，得到以下结论。

（1）双层圆柱面网壳结构的防火设计应同时基于整体结构耐火验算和基于构件耐火验算，取最不利情况作为耐火极限。

（2）基于整体结构耐火验算可采用考虑屈服阶段的本构关系，将计算不收敛时的时间作为结构整体破坏的耐火极限时间，但需要注意排除数值计算不收敛的情况。

（3）由于钢结构耐火验算是基于承载力极限状态，火灾下允许钢结构发生较大的变形，因此将竖向位移作为结构整体失效指标时需作出竖向位移随时间变化曲线，选取拐点处时间作为耐火极限时间。

（4）为了避免局部杆件失稳影响整体结构，双层圆柱面网壳结构的支座设计应尽可能释放水平方向约束。