基于突变理论的水上交通安全状态评价体系

刘进来 杜子俊 李 磊

（武汉理工大学，湖北武汉 430063）

全球海洋面积占地球表面积的75%左右，海洋是人类生存和持续发展的重要基础[1]。海洋经济作为我国经济的重要组成部分，其研究意义不言而喻[2]。水路运输相较于其他运输方式具有运力足、运量大、运费低等优势[3]。我国作为海洋大国，其国际贸易货物运输总量的90%以上是由水路运输的。《全国海洋经济发展“十三五”规划》提出要扩大海洋经济领域开放合作，建设海洋强国[4]。在此背景下，特定水域内的船舶密度显著升高，港口、码头和内河航道尤为突出，随之而来的是水上交通事故的发生风险日益增加。船舶一旦发生碰撞、搁浅等水上交通事故，将对船舶自身、船员和周边环境造成巨大的损害。因此，建立有效的船舶水上交通安全状态评价体系尤为重要。

在以往研究中，将突变理论用于水上交通安全状态预警的相关研究暂时较少。王焕新[5]等利用N-K 模型对海上交通风险因素的耦合进行分析，得到风险耦合因素与海上交通事故发生率的关系。谷磊[6]等将案例推理技术引入水上预警指挥系统，并建立相应的水上应急案例数据库。冯如[7]等将FDA事故致因模型应用于海上船舶事故安全管理，完整表达了海上船舶碰撞事故的发生过程及机理。李政良[8]等结合马尔科夫模型建立GM-Markov 模型用于船舶水上交通事故的预测。陈婷婷[9]等为解决传统故障树分析方法的灰色性和模糊性的问题，引入灰色模糊关联分析方法以计算船舶搁浅事故模糊故障树的模式与事件关联度。万兴岳[10]等将多源信息融合技术运用于水上交通安全预警。高宁[11]等基于HFACS和Apriori 算法对船舶碰撞事故的致因进行分析，识别了从显性原因到隐性原因的致因因素。国内学者在此前运用突变理论对各领域进行了深入的研究但将其引入对水上交通安全状态评价的研究相对较少。船舶水上交通安全状态在事故发生前后具有非连续的特点，突变理论可以很好的描述这一过程，通过对各指标进行归一化运算得出不同时刻下船舶的安全状态。

1 突变理论

1. 1 突变理论简介

突变理论出现于1972 年，由法国的数学家Thom 率先提出，是数学学科的一个新分支。其主要目的是用来研究自然界的不连续现象或状态。该理论所采用的方法是在不同的拓扑结构中先将各种突变进行规范化运算，并根据所采用的势函数对间断点进行分类，再对间断点附近函数的连续性进行讨论，基于此思想，诞生了蝴蝶、抛物、双曲、椭圆、燕尾、折叠、尖点共七种突变模型。突变理论拥有深厚的数学理论基础，其衍生的范围包括了拓扑学、流形、群论以及奇点理论等众多领域。近年来利用突变理论对各领域进行的研究也日新月异，栾婷婷[12]等利用突变-流变理论对滑坡预警体系进行研究。范忠洲[13]等将突变理论引入海底隧道通航安全评价体系并验证了其有效性。王小金[14]等基于突变-流变理论对受困人员的心理进行了研究。赵鹏飞[15]等利用突变理论对突发事件的群体心理发展规律进行描述。谢学斌[16]等基于突变理论验证了采空区群系统的稳定性。杨亚东[17]等用突变理论分析了道路交通事故的致因机理。杨旭[18]等基于突变理论建立了人车碰撞风险实时预警模型。胡华[19]等用突变理论对软土加速流变滑移失稳实验进行分析。

表1 常用突变模型

1. 2 初等突变类型

任何一个系统总有向新的稳定状态转变的趋势，某个系统由旧的平衡状态变迁到新的平衡状态时，在转变的这一时刻就发生了突变，可以用一个光滑的平衡表面（突变流行）来描述这个突变的过程。千差万别的突变现象，以其平衡曲面来分类。经过严密的数学推导，Thom论证了在逐渐变化的控制状态中出现了状态变量的突变，在不超过4维的控制变量和不超过2维的状态变量下，即诞生了蝴蝶、抛物、双曲、椭圆、燕尾、折叠、尖点共七种突变模型，其中应用最广的是尖点模型。

1. 3 尖点突变

尖点突变模型作为最常见、应用最广泛的突变模型，其只有一个状态变量和两个控制变量，计算平衡状态时方程的解较为简便，故采用该模型建立水上交通安全状态评价体系，对不同时刻船舶的安全状态进行描述。尖点突变模型的势函数的计算公式为：V(x)=x4+ux2+vx公式中，状态变量是x，控制参数的变量是u、v，势的函数值是V(x)，即在x状态时，整个系统所包含的能量。当系统状态没有突变，即在平衡态时，有V(x)′=0，即平衡曲面方程为4x3+2ux+v=0, 此三次方程的实根为一个或三个，其判别式为：Δ=8u3+27v2,计算Δ,若其大于0，方程有一个实根；若其小于0，方程有三个不等的实根；若其等于0，则方程至少有两个不等实根（u、v均不为零）或者三个相等的实根（u=v=0）。突变流形图是由曲面方程V(x)＇=4x3+2ux+v=0 所确定的，图1 描绘了当x处于不同状态时函数值V的变化情况，其中三个可能出现的平衡状态由上页、中叶、下页来表示，当函数值V处于上页或下页时，系统是稳定状态，而函数值V处于中叶时，系统处于不稳定状态。任何一个系统从上叶到达下页或从下叶到达上页必须要经过中叶，那么此时系统就是由稳定阶段经过突变达到不稳定阶段的突变过程。

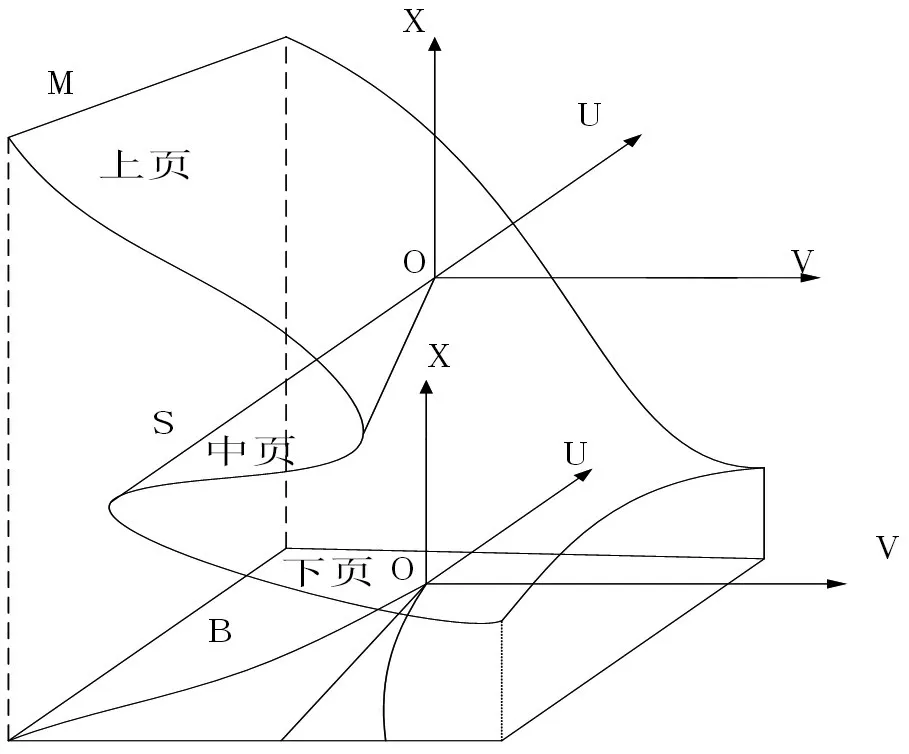
图1 尖点突变模型图

1.3.1 规范化（标准化）公式

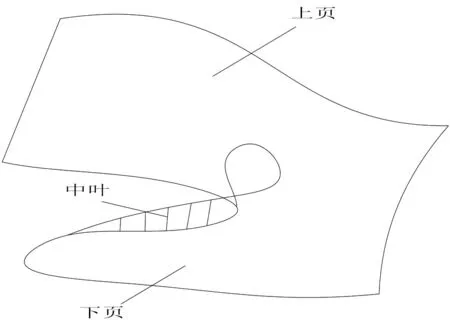
图2 突变流形图

在初等模型的基础上，将各个分歧方程进行汇总，从而得出最终的规范化（标准化）模型，然后运用规范化（标准化）模型对各级指标体系规范化运算得出上一级指标值，循环此计算过程直至得出最终的系统状态变量。规范化（标准化）公式是突变级数的另一个名称，二者本质相同。在不超过四个系统控制变量且只有一个系统的状态变量时，有三种模型可以适用，分别是尖点突变模型、燕尾突变模型和蝴蝶突变模型。

机制所采用的尖点突变模型的规范化（标准化）计算公式为：Xu=u1/2，Xv=v1/3，燕尾突变模型归一公式为：Xu=u1/2，Xv=v1/3，Xw=w1/4，另一种蝴蝶突变模型的规范化（标准化）计算公式为：Xu=u1/2，Xv=v1/3，Xw=w1/4，Xt=t1/5。公式中，u、v、w、t为控制变量，Xu、Xv、Xw、Xt为各控制变量相应的突变级数。

1.3.2 方案优选的计算过程

（1）首先对所评估的系统进行全面的分析研究，在此基础上建立各个层次的由一级指标到二级指标的分层次的评价机制；

（2）对最低层次的指标（二级指标）的数据进行标准化计算，使其变为介于0和1之间的状态值，此状态值即为上一级指标的状态值；

（3）从最低层次的二级指标依次向上利用规范化（标准化）计算公式计算上一级指标的状态值，重复此计算过程直到计算出最顶层的变量状态值。

（4）第（3）步得到的顶层变量状态值就是描述系统此时是否稳定的变量，根据不同需求，即可对所需的方案做出挑选。

由上至下建立从顶层到最低层的多指标评价机制时，若一个一级指标下包括2 个二级指标，则两个二级指标就是状态变量，依次建立尖点突变系统。同理，若一个一级指标下包括3 个二级指标，即可建立燕尾突变系统。如果一个一级指标包括4个二级指标，即可建立蝴蝶突变系统。当一个一级指标下包含的二级变量多于4个时，就要对二级变量在进行下一级的划分，进一步分为子指标的控制变量在4 个以内的突变系统。由于突变模型的规范化（标准化）计算公式所采取的是互补的原则，即可弥补其他控制变量的不足。当各个控制变量不可相互弥补时，则选取控制变量中最小的一个作为变量值。若系统各变量可相互弥补，则取各个控制变量的平均值，这就是“互补”原则。

2 基于突变理论建立安全状态评价体系

2. 1 水上交通风险因素的耦合

根据安全学原理采用人-船-环境-管理四个因素间的耦合来计算船舶的安全状态。

2.1.1 人为因素

现已广泛认同人的因素是大多数水上交通事故发生的主要原因[20]。人为因素包括船员的理论和技术水平、交流沟通能力、身体和心理状况等。理论和技术水平低的船员将不能准确按照《避碰规则》的要求采取行动，无法掌握和使用良好船艺[21]。船员的交流沟通能力差则会导致无法准确传达关键信息，可能会造成相互间的行动不协调。身体和心理状况则会直接影响船员是否能全身心地投入到船舶驾驶工作中。

2.1.2 船舶因素

船舶因素也是导致水上交通事故的重要原因，包括船舶种类、船舶尺度、船龄船况等。

2.1.3 环境因素

环境因素是导致水上交通事故的重要诱因，主要包括天气状况、交通环境、航行水域等。天气状况主要是指航行时的风、流、浪、能见度等因素。交通环境主要包括航行水域的船舶密集程度和助航设施等因素。航行水域主要指可航宽度、航道水深等条件。

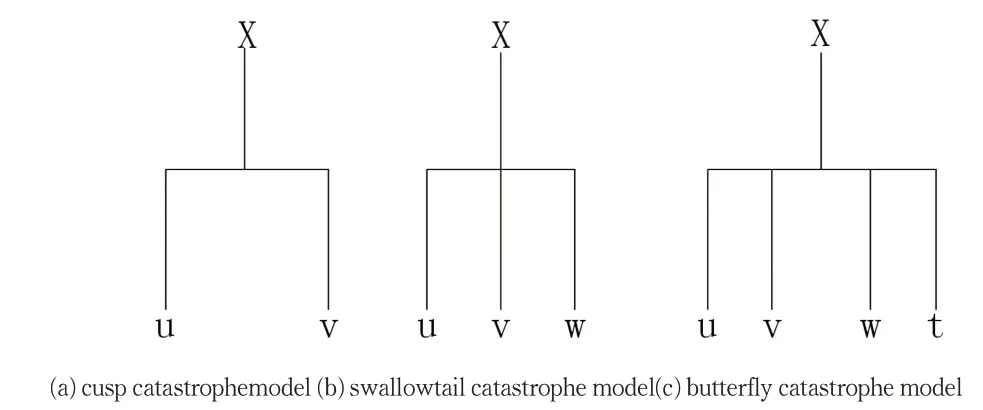
图3 突变模型示意图

2.1.4 管理因素

管理因素同样是导致水上交通事故的重要原因之一[22]，其主要包括内部管理和外部管理等因素。内部管理因素主要是船舶管理，其又包括船舶的安全管理体系和船员的培训演习等。外部管理则主要是海事机构管理和航运企业的管理。

2. 2 风险评价体系

基于上述突变理论，建立水上交通安全状态评价体系，各个子指标通过尖点突变或燕尾突变归一公式无量纲化耦合后得到上一级指标的状态，由下至上循环此过程，可得到船舶在不同时刻的安全状态。构建各控制变量指标集合时应遵循一些共同的原则，包括目的性、全面性、层次性、可行性、独立性等。

图4 水上交通安全状态评价体系

2. 3 基层评价指标的结构重要度和概率重要度分析

2.3.1 结构重要度计算人、船、环境、管理四个一级指标相互独立，显然一级指标下的十一个二级指标也是相互独立互不干扰的。现将十二个二级指标依次命名为X1-X11, 得到最小径集分别为：{X1X4X7X10}、

2.3.2 概率重要度分析

2. 4 评价体系的有效性分析

对构建完成的水上交通水上交通安全状态评价体系进行有效性分析和验证。检测评价指标的有效度和信度。

2. 4. 1 效度计算

各控制变量指标的效度主要是由内容效度比CVR（Content Vadlidity Ratio）来衡量的。其计算公式为：

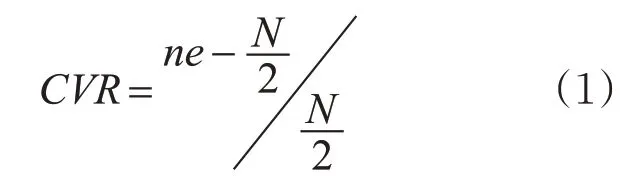
式中N 为参与此次效度评价的总人数，ne为所有参加评价的人员中肯定该指标的预警作用的人数。对于所建立的评价指标，共咨询15 位水路运输领域专家意见，专家的可信度主要从其行业经历、科研成果两方面进行衡量。最终计算得各指标的内容效度比如下：

表2 水上交通安全状态评价指标的CVR值

由计算所得的CVR值以及评价结果定义表分析可知，约91%以上的指标的内容效度比大于等于0.7，即该指标的选取得到了14 位及以上专家的认可。由表3 所列安全状态指标评价结果定义说明专家一致认为所选评价指标符合实际情况。

表3 安全状态指标评价结果定义

2.4.2 信度检测

水上交通水上交通安全状态风险评价体系指标的效度计算完成后，需计算克朗巴赫内部一致性系数来检测评价体系指标的信度。克朗巴赫内部一致性系数的计算公式为：

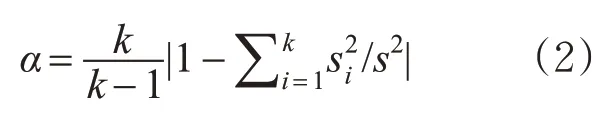
公式中，k为所建立的风险评价机制中所包含的指标个数，Si为计算所得的各指标的标准差，S2为整个样本的方差，Si2为第i个指标的方差。计算得出所建的风险评价体系的克朗巴赫内部一致性系数大约为0.82，由信度评价等级表（表4）可知构建的预警指标体系信度高，符合风险评价指标的构建要求。

表4 信度评价等级

2.4.3 水上交通风险级别评价标准划分

为了对水上交通安全的状态进行最终评价，此处引入一个风险等级的概念，将风险等级由低到高划分为五个等级，等级越高表示风险越大。各个等级对应的隶属度的值分别是0-0.2，0.2-0.4，0.4-0.6，0.6-0.8，0.8-1。但此方法由于逐一向上做标准化计算后，各层的突变隶属值较大，且各等级之间区分度不高，故此处将所得分数变换对隶属值进行修订，可提高评价结果的准确性。

3 案例验证

3. 1 “东方之星”事故发生前的水上交通安全状态评价

鉴于水上交通安全状态的评价是一个相对模糊化的过程，且受到各方面因素的影响无法实地调研某一特定水域以验证所提出评价体系的准确性，故在此采用2015年发生的“东方之星”事故，根据事故调查报告等官方文件中的数据，采用问卷调查和专家打分的方法，对事故发生前各个指标的状态进行模糊评价，并取评语所占比例最大者为最终评语，进行标准化运算后得出各指标无量纲值，见表6。本次问卷发放共30份，主要面向国内航海院校教师和资深航院安全专家发放，有效问卷数为25 份，有效率超过80%。

表5 x-y对应关系表

表6 东方之星事故部分数据

表7 各指标无量纲值

3. 2 评价结果及分析

结合表8 和表5，可知东方之星事故发生之前该水域的安全状态总突变隶属值为0.9982，仅低于1，风险等级为1 级，即风险极高，且各二级指标中环境因素的突变隶属值最大，达到了0.9999，这也与官方发给出的结论：“东方之星”号客轮翻沉事件是一起由突发罕见的强对流天气（飑线伴有下击暴流）带来的强风暴雨袭击导致的特别重大灾难性事件相一致。与传统评价方法相比，突变理论对各指标的重要性排序较为注重，消除了传统评价方法主观性较大的不足，可以相对客观地对水上交通安全状态进行评价。

表8 各指标突变函数值

4 结 论

在总结各界学者对突变理论的理解和应用后，提出采用突变理论对水上交通安全状态进行评价，理论上来说可以基于此方法采用合理的评价指标对水上交通的安全状态进行实时监控和评估。由于数据受限，此处只计算了信度和效度以证明所建立的评价指标符合实际需要，而并未用实际案例对所建立的系统进行规范的验证，诚望读者给予批评指正。

（1）根据水上交通运输的环境特性，选取目前广泛采用的人、船、环境、管理四个风险要素作为一级指标以及船员的理论和技术水平等十一个具体化因素作为二级指标，构建隶属度值与总突变级数的拟合函数f=8×10-6·e11.836x,式中x为总突变级数，f隶属度值，依此建立水上交通安全状态评价体系，对船舶的安全状态进行描述。

（2）结合尖点突变模型和燕尾突变模型对人-船-环境-管理下的各个子指标进行耦合归一化运算，以输出结果来评价水上交通（船舶）的安全状态，通过计算各指标的效度和信度，证明所建立的评价体系基本符合预期。

（3）以“东方之星”事故为例表明该事故发生前的安全风险处于较高等级，采用所建立的评价体系对其进行评价与官方调查报告的结论基本吻合，侧面论证了所建评价体系的正确性和可行性。