改进GWO-RBF神经网络的高频地波雷达海杂波预测模型
何康宁,尚 尚,杨 童,刘 明
(江苏科技大学 电子信息学院,镇江 212100)
高频地波雷达探测海上目标时主要噪声干扰是海杂波,提升雷达目标探测性能的关键在于海杂波的抑制,而海杂波的精确预测是抑制的重要前提.早期,通过研究海杂波概率分布特性,提出了诸多统计模型[1],但从精度和泛化能力方面来说都不足以准确预测海杂波[2].进一步研究发现,海杂波具有混沌特性[3],在短时间内具有实际的可预测性,如果能够生成海杂波内在的混沌动力学模型,就能对其进行非线性预测.从混沌特性出发,对海杂波进行预测和抑制已经取得很多较好的效果[4-5].径向基函数(radial basis funcation,RBF)神经网络强大的非线性函数逼近能力,也给海杂波的非线性预测提供了有力工具.目前,为提高RBF网络性能,各种元启发式算法被用来优化网络的参数[6-7],网络的总体性能得到进一步提升.
灰狼优化(grey wolf optimization, GWO)算法[8]收敛速度快,参数少,易于实现.文中对GWO种群的搜索策略进行改进,提出一种改进灰狼算法优化RBF神经网络的海杂波预测模型.改进的灰狼种群在迭代过程中始终兼具大范围搜索和局部探索的能力,加快了收敛速度和精度,用改进的灰狼算法对RBF神经网络的数据中心、数据宽度和网络权重进行寻优,提高了神经网络预测模型的精度.
1 改进灰狼优化算法
灰狼优化算法采用3个灰狼个体对预估的最优值进行包围,共同引导其他个体向最优值靠近,方向性更强,收敛速度更快.但是整个狼群对全局和局部搜索没有明确的分工,容易陷入局部最优.改进的灰狼优化算法解决了搜索分工上的问题,增加了灰狼搜索最优值的灵活性.
1.1 标准灰狼优化算法
灰狼算法模拟狼群的狩猎行为,首先将狼群按照等级划分为α、β、δ、ω4类灰狼,α狼是狼群中的最高决策者,β和δ狼协助α狼共同引导ω狼向猎物靠近,最终做出进攻.用数学语言描述:每一个灰狼个体的位置都是解空间当中的一个解,前三个最优解分别表示α、β和δ狼的位置,其余解均为ω狼位置.每次迭代,用前3个最优解估算最优值位置,引导灰狼在最优解周围随机更新位置,不断逼近最优解,图1为寻优示意图.

图1 灰狼算法寻优示意图
灰狼个体的位置更新为:
(1)
(2)
(3)
式中:A和C为随机量系数,为:
A=a(2r1-1),C=2r2
(4)
式中:r1,r2为[0,1]之间的随机数向量;a为收敛因子,a的值从2线性递减到0,a越大,搜索范围就越大.狼群在寻优过程中,可以通过调整A和C值控制搜索的步长,由于A和C中均含有随机数,所以灰狼可以向最优值周围的任意方向进行搜索[9].每一次迭代之后,都要根据适应度值重新分配灰狼等级,多次更新之后,最后一代的α狼所在位置即为寻得的最优解.
1.2 改进灰狼优化算法
标准灰狼算法中,收敛因子a的值从2线性递减到0,所有灰狼个体的搜索范围都遵循着同样的策略,前期所有灰狼都进行大范围搜索,阻碍了收敛速度;后期所有灰狼个体都进行小范围探索,忽略了周围解的信息,容易陷入局部最优.种群中没有明确的关于搜索范围的分工,搜索缺乏灵活性.
为了增加灰狼搜索的灵活性,设置适应度阈值ε,将种群分为精英狼群和非精英狼群两个子种群,阈值设置为:
(5)
式中:μ为筛选权重,控制精英狼的个数;m为种群中灰狼个数;fi为当前第i个灰狼的适应度值.适应度值小于阈值的灰狼为精英灰狼,否则为非精英灰狼.
精英狼更靠近最优值,所以应该保持小范围搜索,收敛因子a1从1递减到0;而非精英狼因为远离最优值,故需要保持大范围搜索,收敛因子a2从2递减到1.
(6)
式中:t为当前迭代步数;MaxIter为最大迭代步数.
文献[10]提出动态权重策略的改进灰狼算法(improved grey wolf optimization algrorithm,IGWO),处理单峰问题时收敛速度快.为更好的处理单峰问题,在式(3)中加入新的动态权重,为:
ω=6·(|Dα|+|Dβ|+|Dδ|)
(7)
(8)
在实际应用中,通过阈值划分,每一代灰狼个体之间均有明确的分工,精英狼的个数根据平均适应度值动态变化,有利于提高搜索的灵活性,进一步提升算法的收敛速度和精度.
2 改进算法的性能测试
2.1 选取测试函数
对改进算法进行测试,选取6个标准测试函数用于仿真测试,测试函数如表1.为体现文中改进算法的泛化能力,选取的6个测试函数为3个不同类别:f1和f2是单峰函数,f3和f4是多峰函数,f5和f6是固定维数的多峰函数.

表1 6个测试函数的描述
2.2 改进灰狼算法与其他经典算法的对比分析
粒子群算法是较为经典且在多领域均取得卓越成效的优化算法[11-12],将改进PSO算法[13]、标准GWO算法和动态权重灰狼算法(IGWO)3种算法与各种群灰狼优化算法(multi-grey wolf optimization algorithm,MGWO)作对比.4种算法均设置种群规模为30,最大迭代步数为500,改进算法中筛选权重设置为0.2.图2给出了不同算法在测试函数当中的收敛曲线.

图2 测试函数图及其收敛曲线
从仿真结果可以看出,动态权重有利于提升单峰函数的收敛速度和精度,但对于多峰函数,动态权重的加入使得狼群更容易出现“早熟”现象.文中提出的改进算法,对单峰函数采用分工搜索和动态权重策略,对多峰函数仅采用分工搜索策略.与其他三种优化算法相比,所提算法在处理三类不同函数时,均有着优越的收敛速度和精度.为直观的比较算法性能,每种算法独立运行20次,计算每种算法最优值的均值和方差如表2.
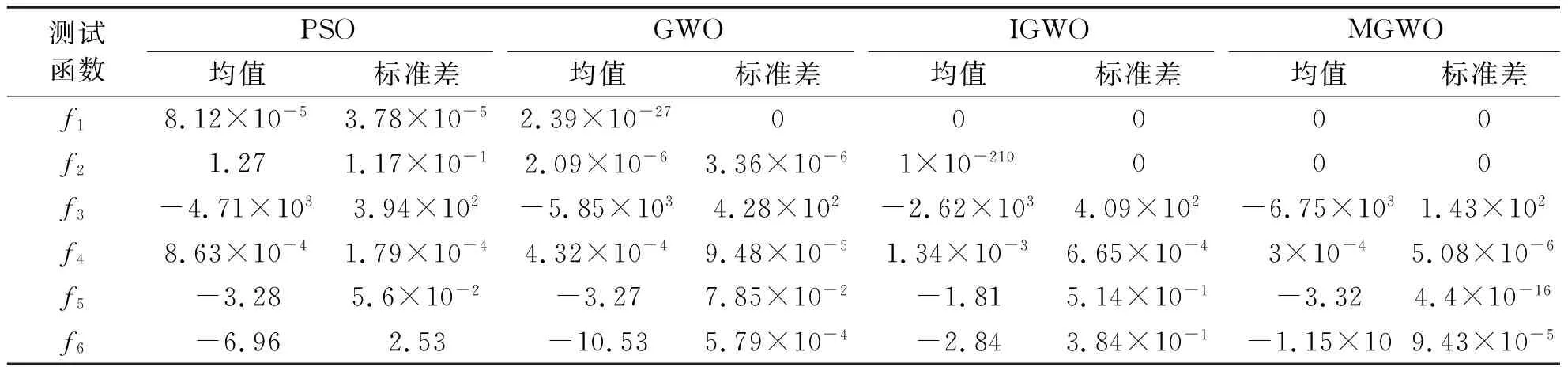
表2 不同算法对测试函数的寻优结果述
从均值的角度来说,改进算法处理单峰函数时可以收敛到0,处理多峰函数时,精度均高于其他三种对比算法.另外,改进算法在处理各类函数时,标准差都明显小于对比算法,说明改进算法的稳定性更高.
3 改进MGWO-RBF模型用于海杂波预测
3.1 预测模型的构建
通过相空间重构的方法,生成海杂波混沌动力学系统在重构的高维相空间中的一条轨迹,该轨迹即为产生海杂波非线性系统状态转移方程F的样本,即yi+1=F(yi),又可以写成:
(xi+τ,xi+2τ,…,xi+mτ)=F(xi,xi+τ,…,xi+(m-1)τ)
(9)
式(9)中等式左边任意一项都受到等式右边所有项的影响,故又可以写成:
xi+mτ=f(xi,xi+1,…,xi+(m-1)τ)
(10)
为了能使方程具有更大的灵活性和函数概括能力,文献[14]在等式右边加入更多的过去变量,得到海杂波的预测方程:
xi+mτ=f(xi,xi+1,…,xi+mτ-1)
(11)
式中:τ和m分别为相空间重构的两个重要参数,即时间延迟和嵌入维数.
利用RBF神经网络学习式(11)的复杂映射关系,通过训练网络得到海杂波的预测模型.采用文中改进的灰狼算法对网络的初始参数进行寻优,从测试函数实验中看出,MGWO算法寻优的精度更高,因而种群寻得的网络初始参数更加接近最优的初始参数,在此基础上,训练得到的网络模型预测精度可以得到进一步提升.算法寻优的对象包括数据中心、数据宽度和网络权重.MGWO迭代过程中根据网络的误差来评估适应度值,适应度值为:
(12)

海杂波预测模型的建立步骤如下:
(1)确定网络模型结构,将数据中心c、数据宽度σ以及网络权重ω编码生成灰狼的位置矢量.设置灰狼种群规模,对灰狼个体的空间分布进行混沌初始化.
(2)用文中改进的灰狼优化算法,在解空间中搜索适应度最小值,将最后适应度值最小的灰狼个体对应的位置矢量还原成网络参数,作为网络的初始参数.
(3)将不含目标的海杂波信号进行归一化处理,从处理后的海杂波时间序列中构造训练数据.
(4)设置期望达到的网络精度与最大训练次数,训练网络直到满足预设条件后停止,训练得到的MGWO-RBF神经网络模型即为海杂波的预测模型.
(5)用预测模型对临近距离单元的海杂波进行预测.
网络模型的预测精度为:
(13)

3.2 实验结果及分析
采用威海高频雷达的海杂波实测数据进行实验.雷达的工作频率为3.7 MHz,采样间隔为0.149 s.实测数据分为I通道和Q通道,这里以I通道的数据为例.用第30个距离单元的数据构造训练数据,分别以第35、第45个不同距离单元的数据作为测试数据.
由经典的C-C算法[15]计算得到海杂波的时间延迟τ=4,嵌入维数m=3,故网络的输入节点数为mτ=12,输出节点数为1,设置隐层数为4.用优化算法对网络初始参数寻优时,设置种群规模为25,最大迭代次数为300.在相同条件和环境下进行实验,图3给出了不同优化算法在寻找网络最优初始参数时适应度值的收敛曲线.
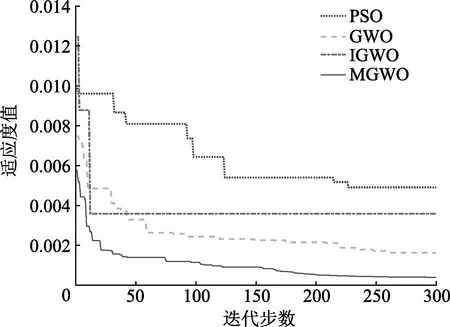
图3 适应度值收敛曲线
所要求解的问题是一个多峰问题,图中IGWO算法过早的进入稳定,进一步暴露了动态权重策略面对多峰问题的劣势.标准的灰狼算法相比于经典的粒子群算法,无论是在收敛速度,还是在精度方面都有较大的提升.文中MGWO算法在GWO先天优势的基础上,进一步提升性能,寻优的精度更高,在几种算法中表现最好.
不同优化算法寻优得到的最小适应度值不同,因而得到的网络初始参数也不同.为了验证最小适应度值对预测精度的影响,以及表现各类模型的预测性能.用第30个距离单元的数据构造500组训练数据训练网络,期望精度MSE=0.01,训练次数为1 000次.将训练得到的神经网络预测模型分别用来预测两个不同距离单元的海杂波,不同算法均独立实验20次取结果的均值,表现效果如表3.

表3 预测效果比较
实验过程中,不经过优化的网络模型在训练的时候稳定性不高,影响最终的预测效果.从表3中可以看出,优化后的RBF神经网络预测模型在稳定性和精度上均有提升.最小适应度值的大小反映了寻优得到的网络初始参数的优劣,适应度值越小,说明得到的网络初始参数越好,最终训练得到的模型预测精度越高.表中MGWO优化算法得到的适应度值最小,因而MGWO-RBF网络模型的预测精度最高,在预测第35个距离单元的海杂波时,精度较RBF预测模型提升了10.97%,较PSO-RBF预测模型提升了5.06%,较GWO-RBF预测模型和IGWO-RBF预测模型分别提升了2.67%和3.72%.可见,文中改进的灰狼优化算法优化RBF神经网络,使得模型的预测精度明显优于对比算法.另外,预测模型对第35个距离单元海杂波的预测精度总是略高于对第45个距离单元海杂波的预测精度,这与训练数据的选取有关,说明两个距离单元相距越远,海杂波的内在动力学特征的差异性就越大.
图4为训练好的MGWO-RBF神经网络预测模型对两个不同距离单元海杂波的预测效果.MGWO-RBF神经网络预测模型能够很好的对海杂波实现预测,预测精度较高,为海杂波的抑制提供了重要依据.

图4 海杂波的预测效果
4 结论
(1)根据灰狼种群的平均适应度值设置阈值,动态的将种群分为两个子种群,执行不同的搜索策略,提高了灰狼算法的收敛速度和寻优的精度,减小了灰狼算法陷入局部最优的概率.
(2)用改进的灰狼算法优化RBF神经网络初始参数,构造MGWO-RBF预测模型预测海杂波,通过与对比模型比较,发现MGWO-RBF神经网络预测模型预测精度最高,达到96.23%.
(3)文中提出的海杂波预测模型能够较为准确地对海杂波进行预测,在进一步的海杂波抑制方面有着良好的应用前景.

