结合“鸡兔同笼”问题看数学作业设计与实践
葛慎双
摘要:数学课程标准要求鼓励解决问题策略的多样化,用不同的知识和方法解决问题。“鸡兔同笼”问题是我国广为流传的数学趣题,文章从“鸡兔同笼”问题出发,看数学作业设计与实践。
关键词:鸡兔同笼;数学作业;设计与实践
“鸡兔同笼”问题是我国民间广为流传的数学趣题,大约一千五百年前,我国古代数学名著《孙子算经》中就有记载。同时,这个问题传到日本变成了“龟鹤问题”等等,有许多类似的问题需要我们用相应的方法去解决。“鸡兔同笼”是个很抽象的问题,学生该用什么方法来解题呢?
《数学课程标准》指出:“教学中应尊重每一个学生的个性特征,允许不同的学生从不同的角度认识问题,采用不同的方式表达自己的想法,用不同的知识与方法解决问题。鼓励解决问题策略的多样化,是因材施教、促进每一个学生充分发展的有效途径。”立足小学数学学科实际,深入开展学生作业设计研究,不断增强作业的开放性、关注学生的个性差异,不断增强作业的层次性、适应性、可选择性、满足学生的不同需求。
《孙子算经》中记载的问题是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。问笼中各有几只鸡和兔?结合此题作为例题,进一步探究数学作业的设计与实践。
例题:有若干只鸡、兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。问笼中各有几只鸡和兔?
一、用画图的方法解题
先让学生画35个圆圈表示35个头,再在每个动物下面画两条腿,35只动物只用了70条腿,还多出24条腿,把剩下的24条腿要给其中的几只动物添上呢?(一只鸡是两条腿,一只兔子是四条腿;一只兔子比一只鸡多两条腿。12只动物分别各添2条腿正好是24条腿)。这12只就是兔子,另外的23只就是鸡。接着老师问能把动物都看成是4条腿的吗?自己再动手画画:画35个圆圈表示35个头,再在每个动物下面画四条腿,35只动物共用了140条腿,这时少了46条腿,这46条腿是其中哪几只动物少的呢?(23只动物分别各少2条腿正好是少46条腿)。这23只就是鸡,另外的12只就是兔子。
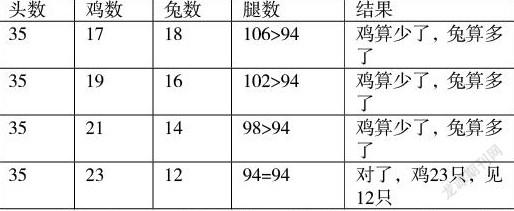
二、用列表的方法解题
用列表的方法解题,把头数平均分,使鸡和兔的数量一样多(如果不能平均分的,它们只能相差一只),这样试算才能较快找到正确的答案。在试算时,鸡和兔的数量有时一个一个地增减,也可以二个或多个地增减,要看正确的腿数与试算的腿数的差是多少来决定,如果这个差越大,增减的数也就越大;反之就小。
三、用假设法解题
(一)解法一:
假设都是鸡,35只鸡应有脚:35x2=70(只)
与实际比少算的脚数:94-70=24(只)
有一只兔当一只鸡就少算脚数:4-2=2(只)笼中实际有的兔数:24÷2=12(只)笼中实际有的鸡数:35-12=23(只)
(二)解法二:
假设都是兔,35只兔应有脚:35x4=140(只)与实际比多算的脚数:140-94=46(只)
有一只鸡当一只兔就多算脚数:4-2=2(只)笼中实际有的鸡数:46÷2=23(只)笼中实际有的兔数:35-23=12(只)
运用假设法解题时,要根据题意正确的进行假设,并要依据假设按照题目所给的数量关系正确的进行推算。在解答这类題目时,要求学生把思考的过程全部写下了,找到解题的方法。
四、可用解方程方法解题
1、解:设兔有X只,那么鸡就有(35-X)只。4X+2(35-X)=94
2、也可设:设鸡有X只,那么兔就有(35-X)只。2X+4(35-X)=94,可求出23只是鸡,12只就是兔子。
通过上述的讲述,这就要求教师在作业的设计时要从培养学生多种能力和创造精神的目标出发,从实际生活出发,多层次,多角度地设计作业。通过课堂检测把握每个学生的学习结果,布置作业时根据学生掌握情况分层次布置作业。在内容上,坚持定量与定性的结合,在需求上,不得利用教辅资料布置作业。让学生有较充裕的时间,进行其多样化、个性化的学习。使作业真正起到促进学生学习的作用,从而充分发展学生的天性,锻炼学生的能力。
五、注重作业设计的实践性
作业设计要符合素质教育要求,紧密结合课程标准和学习内容,既要体现小学数学学科整体的计划性,又要体现课时目标的针对性,还要体现认知水平的层次性;要关注学生的个体差异和发展需求,要充分考虑学生心理特点、生理特点、认知特点和承受能力,精心筛选、难易适度、总量控制,要有创造性、科学性、趣味性,努力提高学生完成作业的兴趣,减轻学生心理负担,达到以点带面、举一反三、触类旁通的目的。要沟通知识间的内在联系,鼓励学生进行探究,发展学生的思维能力,提高学生动手操作能力。
六、注重数学思想的渗透
“鸡兔同笼”是我国民间广为流传的数学趣题,教学中揭去了它令人生畏的奥数面纱,还其生动有趣的一面。通过学习,不仅使学生感受祖先的聪明才智,而且体会到解题策略的多样性以及其中蕴含的丰富的数学思想方法,培养学生的学习兴趣和能力。作业设计既关注了学生解决问题的结果,更关注了学生解决问题的过程与方法,并在不断提升学生解决问题的技能技巧。
作业设计与布置实践的过程实际上是对理论认识的再现过程,同时也是一个不断修改、提高、完善的过程,从理论的学习中进行作业设计,从作业设计中加深对理论的理解。只有掌握了一定的解题策略,才会在遇到问题时,找到问题的思考点和突破口,迅速、正确地解题,因此在教学中我们要适当加强数学解题策略的指导,优化学生的思维品质,提高解题能力。

