基于扰动观测器和重复控制的转速脉动抑制

陈九霖，郭昊昊，刘彦呈，于春来，李冠桦

(大连海事大学 轮机工程学院，辽宁 大连 116026)

0 引 言

永磁同步电机由于具有结构简单，功率密度高的优点得到了越来越广泛的应用[1]。然而由于转速脉动的存在严重影响了永磁同步电机在要求高转速精度工况下的应用，且转速脉动还会降低电能利用率和元器件的使用寿命，给系统带来不稳定的隐患，因此对于转速脉动抑制的研究具有重要意义[2]。

转速脉动产生的原因主要有：逆变器的死区效应，电流测量误差，磁链谐波，齿槽转矩等[3]。而对于死区效应和电流测量误差这两种非理想因素带来的转速脉动的抑制，国内外学者做了大量研究。其中对于死区效应的解决方案主要为电压补偿法。文献[4]通过修正SVPWM基本矢量作用时间来消除死区的影响，但功率器件开关时间随负载电流变化可能导致修正有误。文献[5]将补偿电压前馈到电压给定来抑制死区效应带来的影响，但补偿电压的计算依赖于相电流极性的精确检测，实现困难。文献[6]仅通过开环扰动观测来提取死区时间，文献[7]利用广义二阶积分器提取死区造成的电流谐波并进行消除，但两种方法皆存在补偿不准确和实时性差的问题。且仅补偿死区电压仍然会使转速中残留电流测量误差带来的转速脉动。

解决电流测量误差的主要方法为定子电流补偿。文献[8]通过低通滤波器和谐振环节提取转速中电流基频的1次、2次谐波并计算出误差量补偿至电流给定前，但是同样会给系统带来滞后。文献[9]利用电流测量误差引起的电流环控制器输出误差进行补偿量的计算，但提取正负相序电流的环节中仍需低通滤波，这同样会降低系统的快速性。

本文详细分析了死区效应和电流测量误差使得稳态转速产生脉动的机理。提出一种基于扰动观测器的死区时间补偿算法解决死区效应导致转速脉动问题，其中扰动观测器对死区补偿时间进行在线识别，克服了IGBT通断时间随负载电流变化导致补偿不准确的问题，并用重复控制的方法对于电流测量误差导致的残余转速脉动进行了进一步的抑制。仿真结果表明抑制效果良好。

1 死区效应及电流测量误差谐波分析

1.1 死区效应谐波分析

IGBT通断延时可能造成逆变器某相桥臂直通，因此通常需要人为设置死区时间。而设置死区时间会给系统带来一系列的负面影响，即死区效应[10]。用电压源型三相逆变器分析死区效应，以A相桥臂为例，其结构如图1所示，Udc为直流母线电压，Sa+，Da+，Sa-，Da-分别为A相上、下桥臂IGBT和续流二极管。定义电流流入电机的方向为正，此时iAN>0，逆变器通过Da-续流，反之iAN<0并通过Da+续流。

图1 逆变器A相结构图

图2 仅考虑IGBT存在死区时间时的PWM及输出电压波形图

图3 考虑开关时间和通态压降时的PWM及输出电压波形图

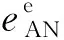
图4 等效偏差电压波形图

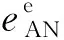
(1)

式中，fe为相电流基频，n取1,3,5,7…。由于电机可近似看作对称负载，因此相电流不存在3次谐波，若忽略高次谐波的影响，则相电压的畸变必然使相电流中含有5次负序和7次正序谐波。为进一步研究畸变的相电流对电机转速的影响，将相电流变换到同步旋转坐标系下，再将5、7次谐波电流d，q轴分量分别投影到基波旋转坐标系中，各次谐波电流d，q轴分量及其投影关系如图5所示。

图5(a)中，d1，q1，d7，q7，d-5，q-5分别为基波电流和5、7次谐波电流的d，q轴分量，且各自以角速度ωe，7ωe，-5ωe沿箭头所示方向旋转，其中θe1=7ωet-ωet=6ωet。将5、7次谐波电流d，q轴分量分别投影到基波旋转坐标系中，各次谐波电流d，q轴分量及其投影关系如图5(b)所示，其中d7,d1表示7次谐波电流d轴分量在基波d轴上的投影，其它各投影分量的命名以此类推。因此，根据图5有：

(2)

图5 向量图

(3)

式中，I7,d1，I7,q1，I-5,d1，I-5,q1分别为相电流中7次和5次谐波在基波同步旋转坐标系中的d、q轴分量。因此，以A相电流为例，其在基波同步旋转坐标系下的d、q轴分量应为

(iA,d=d1+I7,d1+I-5,d1=d1+(d-5+d7)cosθe1-
(q-5+q7)sinθe1
iA,q=q1+I7,q1+I-5,q1=q1+(d7+d-5)sinθe1-
(q7-q-5)cosθe1)

(4)

因此，由式(4)可以看出逆变器的死区效应会给q轴电流带来6次谐波，这将会使电机转速产生6次谐波分量。

1.2 电流测量误差谐波分析

永磁同步电机矢量控制系统需要实时将定子电流采集到DSP中参与控制运算。而实际情况中由于电流传感器供电电压的不平衡及非线性，调理电路中电阻的热漂移，测量噪声等会影响电流的测量精度，导致测量误差的产生。通常将电流测量误差分为增益误差和偏移误差[11]。

含有测量误差的相电流iA_AD和iB_AD在静止坐标系为

(5)

其中iA和iB分别为实际的A相和B相电流，kA和kB分别表示A相增益和B相增益。ΔIA_off和ΔIB_off是偏移误差，I是瞬时电流振幅。那么可以推导出每相电流的测量误差ΔiA，ΔiB，ΔiC为

(ΔiA=iA_AD-iA=(1/kA-1)iA+ΔIA,off
ΔiB=iB_AD-iB=(1/kB-1)iB+ΔIB,off
ΔiC=iC_AD-iC=(1-1/kA)iA+
(1-1/kB)iB-ΔIA,off-ΔIB,off)

(6)

再将ΔiA，ΔiB，ΔiC变换到同步旋转坐标系下，由于表贴式电机电磁转矩只与q轴电流有关，因此只考虑q轴电流误差Δiq为

(7)

其中，

由式(7)可以看出，电流测量误差最终会给q轴电流带来1次，2次谐波。而根据永磁同步电机的转矩方程可知q轴电流谐波会产生周期性的扰动转矩，这样的扰动转矩最终会使电机稳态转速产生脉动[11]。

2 基于扰动观测器的死区时间补偿

2.1 死区补偿时间的计算

由图3可以得出理想死区补偿时间Tc应为

(8)

式中,td，ton，toff，Ts分别为死区时间，IGBT导通和关断时间以及PWM周期。定义udp为IGBT通态压降uS和续流二极管通态压降uD的平均值，即，

(9)

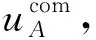
(10)

(11)

(12)

2.2 基于扰动观测器的死区补偿时间估计

永磁同步电机旋转坐标系下的电压方程为

(13)

式中，ud，uq，id，iq分别为d、q轴电压和电流，R、L为定子电阻和同步电感，ψi为永磁体磁链。

令耦合电压ud0，uq0为

(14)

(15)

根据式(15)列写当前系统状态方程，不考虑输出方程，有:

(16)

由式(16)易知系统完全可观测。则观测器状态方程为式(17)，其中观测器增益矩阵K=[k1,k2]T。

(17)

即，

(18)

设观测器的两个极点为γ1和γ2，则推出，

(19)

将式(19)带入到式(18)，不考虑输出方程，则观测器状态方程为

(20)

3 基于重复控制的转速脉动抑制

3.1 重复控制器谐波抑制机理

死区效应引起的电机转速脉动已通过死区时间补偿得到了有效抑制，但是电流测量误差引起的转速脉动仍然影响着转速的平稳性和精确性。单靠带宽有限的PI控制器无法完全抑制周期性的扰动转矩，必须使用重复控制器来对残余转速脉动进行抑制。由于转速环的惯性远大于电流环，因此可以有充足的时间产生重复控制命令[13]。加入重复控制器(Repetitive Controller，RC)的系统控制框图如图6所示，图7为方便后续的参数设计及分析而简化的系统控制框图。

图6 加入RC的矢量控制系统结构图

图7 简化系统控制框图

图8 RC结构图

krc为重复控制器增益，z-N为延时环节，N为扰动电流基波周期与系统采样周期的比值。Q(z)为鲁棒滤波器，C(z)为相位补偿器，其传递函数为

(21)

(22)

理想情况下，鲁棒滤波器Q(z)取值为1，假设系统稳定，当扰动信号为频率为Nωe(N=1,2,3…)的周期信号时，根据欧拉公式有z-N=e-2Nπj=1，可推出此时E(z)为零，扰动得到完全抑制。

3.2 重复控制器参数设计

根据离散系统稳定条件，式(22)分母的根应全部位于z平面单位圆内。令去掉重复控制器后的系统传递函数M(z)为

(23)

认为M(z)稳定，且系统稳定时必有|zN|<1。因此若要系统稳定，只需要满足：

|Q(z)(1-krcC(z)M(z))<1|

(24)

因此要设计的参数有：重复控制增益krc，鲁棒滤波器Q(z)和相位补偿器C(z)。

鲁棒滤波器Q(z)的作用为将对系统影响不大的高频谐波滤除增加系统稳定性，由于滑动平均滤波器具有零相移的特点，因此选择Q(z)为

Q(z)=0.45z-1+0.1+0.45z

(25)

相位补偿器C(z)的作用是补偿系统产生的相位滞后，进一步增加系统鲁棒性。选用线性相位补偿的方式，即C(z)=zm,这种补偿方式可以为系统在ω频率处产生(mω/ωN)×180°的相位补偿，ωN为奈奎斯特频率。将式(24)变成如下向量形式：

|(NQejθQ)(1-krcNMej(θM+mω))|<1

(26)

其中NQ、θQ和NM、θM分别为Q(z)和M(z)的幅值和相角，式(26)右侧第一项恒大于零，因此有：

(27)

即，

|θM+mω|<90°

(28)

因此，可根据式(28)计算相位补偿器的m的值，再根据式(27)选择krc的值，值得注意的是krc的值越大，转速偏差收敛的速度越快，但也会产生较大的超调，一般选择0～1之间的某个值。

4 实验结果

为验证上述基于基于扰动观测器和重复控制的电机转速脉动抑制策略的有效性及动静态性能，搭建基于Matlab/Simulink的永磁同步电动机矢量控制系统模型。系统结构如图9所示。

图9 带有重复控制器和死区时间补偿的系统结构图

表1 永磁同步电机参数

给定转速150 r/min，在0.1 s突加负载0.14 Nm，对称设置死区11 μs，kA和kB分别设为1.15和0.85，ΔIA_off和ΔIB_off分别设为0.2 A和-0.1 A,仅加入死区补偿算法时的仿真结果如图10所示。

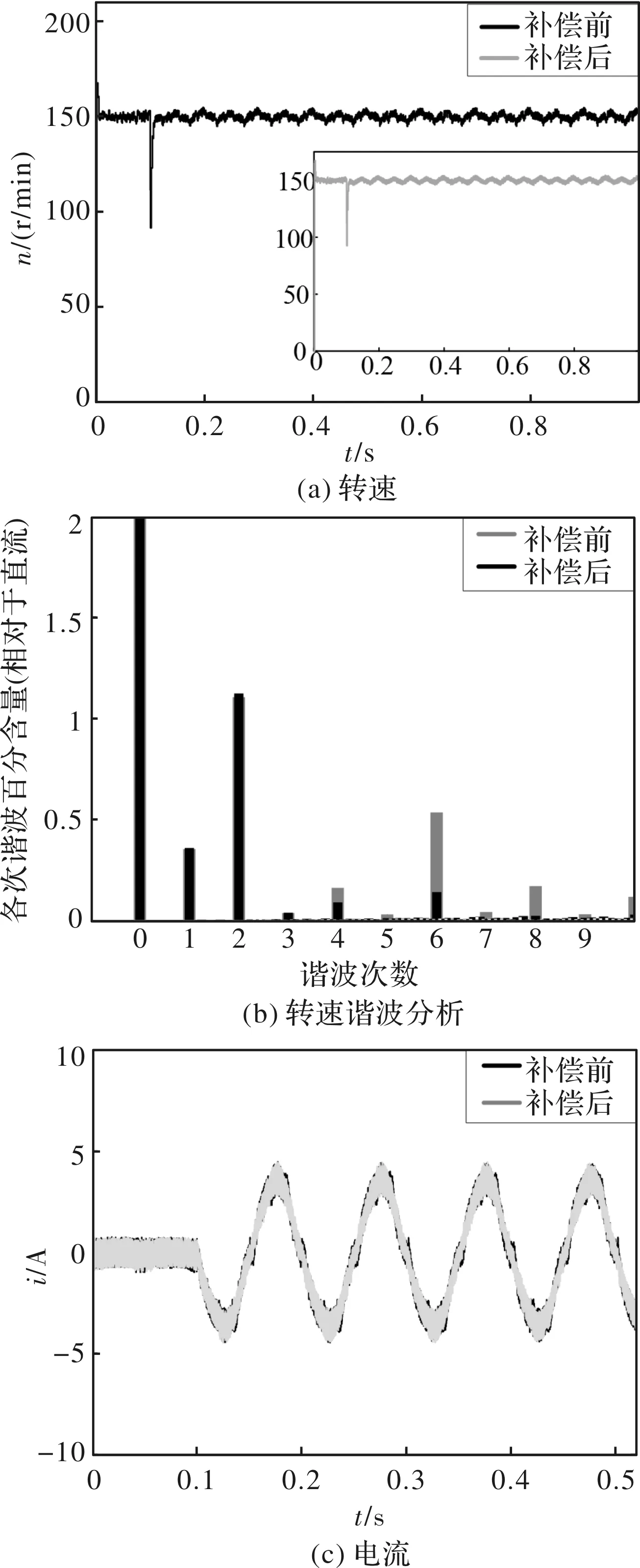
图10 仅加入死区补偿算法时的仿真结果

由图10可以得出所提死区补偿算法对转速中由于死区效应导致的6次谐波具有良好的抑制效果，且对相电流的畸变也有一定的平滑作用，但仍然不能抑制由于电流测量误差造成的1次、2次谐波，因此仍需用RC进一步抑制。加入RC后的仿真结果如图11所示。

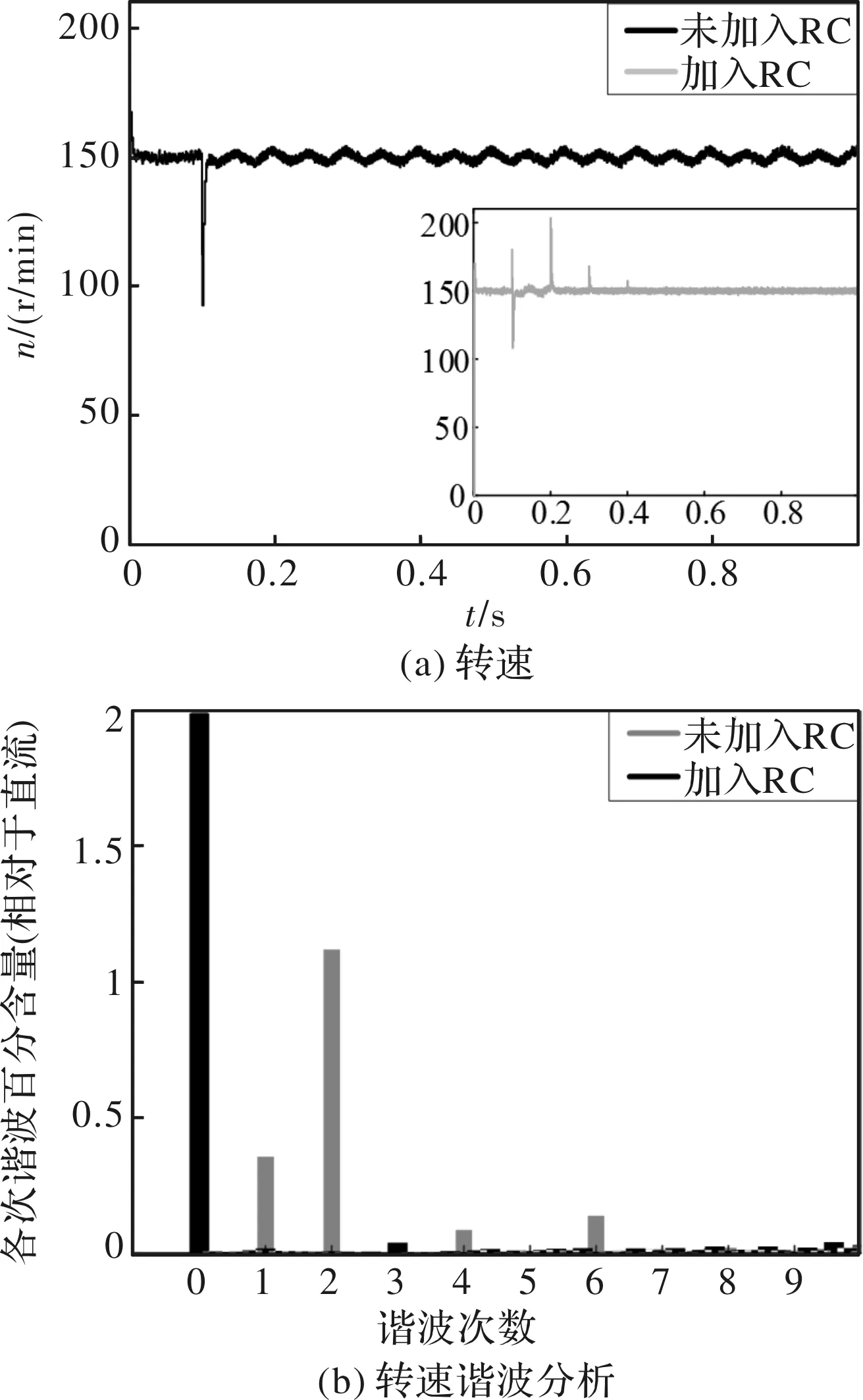
图11 加入RC时的仿真结果

由图11可以得出RC能够有效抑制转速中残余1次、2次谐波，且能够在0.1 s内收敛至给定转速，动静态性能较好。更改给定转速分别为为300 r/min，600 r/min和1500 r/min并设定kA和kB为1.25和0.8，ΔIA_off和ΔIB_off为0.25 A和-0.15 A，仿真结果如图12至图14所示，如图12至图14所示，所提方法仍然能够有效抑制转速中1次、2次和6次谐波。

图12 给定转速为300 r/min时的仿真结果

图13 给定转速为600 r/min时的仿真结果

图14 给定转速为1500 r/min时的仿真结果

5 结 论

本文对逆变器死区和电流测量误差产生转速脉动的机理进行了深入分析，并提出一种扰动观测器与重复控制器相结合的方法对此两种实际工况中必然存在的非理想因素导致的转速脉动进行了抑制。

仿真结果表明，所提方法能够克服传统方法由于IGBT通断时间随负载电流变化导致的补偿不准确的缺点，对逆变器死区导致的转速脉动具有较好的抑制效果。RC也能够快速有效地抑制电流测量误差带来的残余转速脉动，进一步增强了转速的平稳性。该方法提高了永磁同步电机在需要转速高精度工况下的可应用性，具有一定的理论价值和实际应用价值。