三角形中45°角的处理策略

文／沈飞鸿

（作者单位：江苏省苏州市太仓市浮桥中学）

三角形问题大都从“线段”“角度”和“运动方式”这三种角度给出条件和求解，相比于“线段”，诸如30°、45°、60°等特殊的“角度”是同学们在解题中经常会遇到的。本文以2021 年江苏省连云港市的中考题为例，剖析45°角的不同处理方法，帮助同学们用类比的方法了解特殊角的处理策略。

例如图1，抛物线y=mx2+（m2+3）x-（6m+9）与x轴交于点A、B，与y轴交于点C，已知B（3，0）。

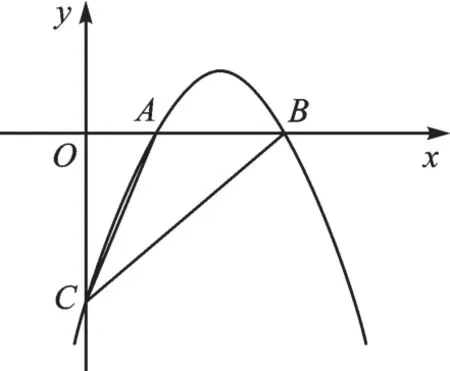
图1

（1）求m的值和直线BC对应的函数表达式；

（2）P为抛物线上一点（与点A不重合），若S△PBC=S△ABC，请直接写出点P的坐标；

（3）Q为抛物线上一点，若∠ACQ=45°，求点Q的坐标。

【解析】（1）（2）两问的答案为：（1）m=-1，直线BC的表达式为y=x-3；（2）P的坐标为（2，1），（。

第（3）问如果从构造等腰直角三角形、构造相似三角形和构造全等三角形这三个角度处理45°角，可以有三种不同的解法。

解法一：如图2，过点A作线段AC的垂线，交射线CQ于点M，过点M作MD⊥AB于点D。

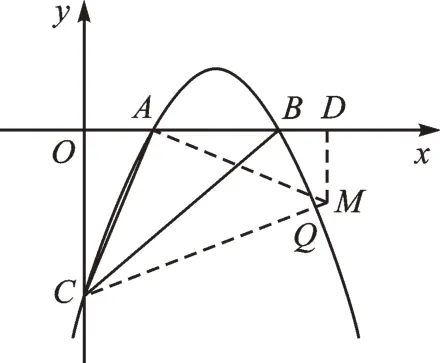
图2

∵A（1，0），C（0，-3），∴M（4，-1），

∴直线CM的表达式为。

∵点Q是抛物线y=-x2+4x-3 与直线CM的交点，∴联立两个方程，解得。

【点评】在直角坐标系中出现等腰直角三角形，很容易想到构造“一线三直角”的“K 字相似形”，等腰又能带来边相等，把相似进一步转化为全等。因此，“构造K 字相似形”和45°角配合起来，有“1+1＞2”的效果。

解法二：如图3，在y轴上取点M、N，使∠AMC=∠QNC=45°。

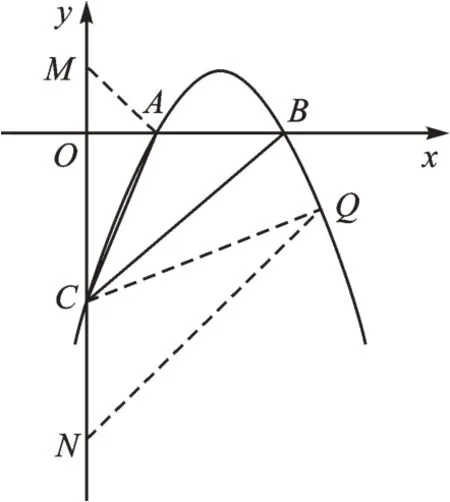
图3

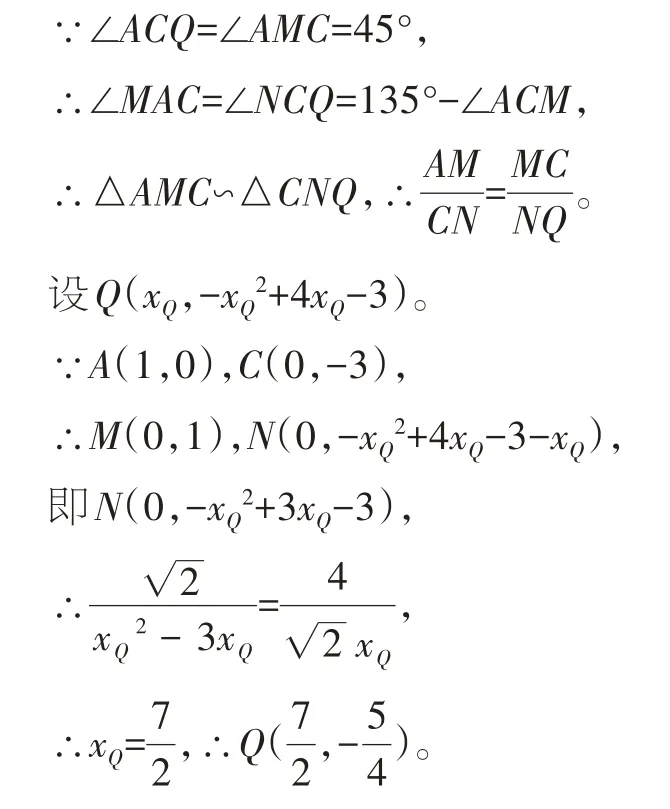
【点评】在y轴上找到点M（点C上方）、点N（点C下方），使得∠AMC=∠ACQ=∠CNQ=45°，则△AMC∽△CNQ，这是常见的构建“一线三等角”相似形的方法。

解法三：如图4，将△AOC绕点C顺时针旋转45°得△A′O′C。

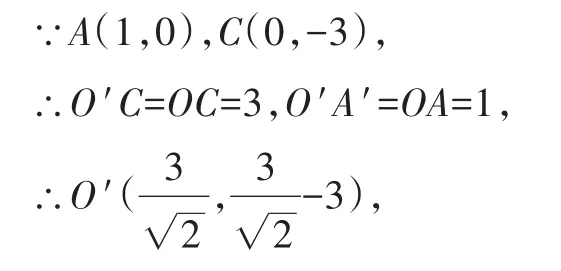
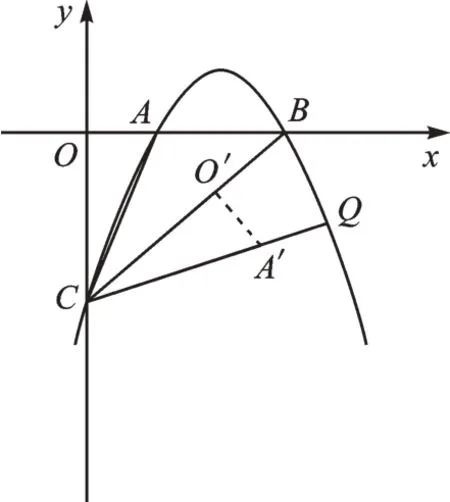
图4

【点评】本题除了有∠ACQ=45°外，还隐含了∠OCB=45°，因此，我们可以把△AOC绕点C顺时针旋转45°，即可求出直线CQ上的一点A′的坐标，从而借助直线CA′的表达式得到点Q的坐标。本解法中的45°角，除了是两条线段的“夹角”外，也可以是三角形旋转前后的“旋转角”。

上面介绍的前两种解法，都是通过构造“一线三等角”的全等形和相似形，把不方便计算的线段AC、CQ，转化成“横平竖直”的或斜向45°的方便计算的线段之间的关系，从而建立方程求解。解法三则是通过旋转45°，将斜向△A′O′C和两边“横平竖直”的容易计算的△AOC建立起全等关系，从而解决问题。这里，变的是45°角的处理方法，不变的是“化斜为直”从而化繁为简的思想方法。