三角形问题中的易错点分析

文／崔曾如

（作者单位：江苏省太仓市双凤中学）

三角形作为几何图形中的基本图形，在初中数学的学习中占有非常重要的地位。很多四边形以及复杂的直角坐标系中的几何图形问题最后都是转化为解决三角形的问题。在解决三角形问题中，同学们容易忽略三角形三边关系、角的分类讨论以及实际问题中隐含的边角关系。下面老师针对三角形问题中的一些易错点进行分析，希望能够帮助同学们避免再次出现这类错误。

一、忽视三角形三边的隐含关系

例1若菱形ABCD的一条对角线长为8，边CD的长是方程x2-10x+24=0的一个根，则该菱形ABCD的周长为（ ）。

A.16 B.24

C.16或24 D.48

【分析】已知条件是菱形，要求菱形的周长，只要计算出菱形的边长即可。求解一元二次方程可以得到线段CD的长度，而线段CD与菱形的对角线刚好构成一个三角形。脱去菱形的外衣，此题其实就是三角形的三边关系。同学们应关注两点：①三角形的任意两边之和大于第三边，②解决几何问题最好画出示意图。

解：画出示意图如图1。

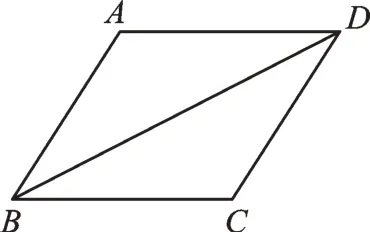
图1

∵四边形ABCD是菱形，

∴AB=BC=CD=AD，

∴菱形ABCD的周长=4CD。

又∵x2-10x+24=0，

∴（x-4）（x-6）=0，

解得x=4或x=6。

①当CD=4 时，4+4=8，不能构成三角形；

②当CD=6 时，6+6＞8，满足三角形的三边关系，符合要求。

二、忽视三角形角的分类讨论

∴菱形ABCD的周长为4CD=24。

故选B。

例2在△ABC中，AD是BC边 上 的高，∠BAD=25°，∠CAD=55°，则∠BAC=______。

【分析】很多同学做错的原因是只考虑了BC边上的高在三角形内部的情况。由于△ABC的形状不确定，所以就不能确定BC边上的高是在三角形的内部还是在三角形的外部，因此本题需要分类讨论。

解：①如图2，高AD在△ABC的内部，则∠BAC=∠BAD+∠CAD=25°+55°=80°；

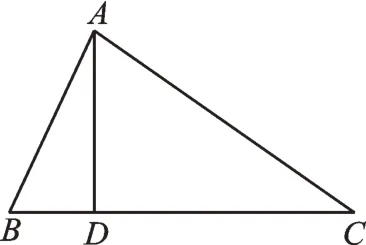
图2

②如图3，高AD在△ABC的外部，则∠BAC=∠CAD-∠BAD=55°-25°=30°。

图3

因此，∠BAC的度数为80°或30°。

三、对三角形变换问题的性质不清楚

例3如图4，在△ABC中，∠BAC=108°，将△ABC绕点A按逆时针方向旋转得到△AB′C′。若点B′恰好落在BC边上，且AB′=CB′，求∠C′的度数。

图4

【分析】本题是三角形旋转运动问题，很多同学在遇到这类题型时弄不清谁在旋转，绕着哪个点旋转，旋转后得到了什么等问题。旋转变换给我们带来的是线段和角的关系。本题中△ABC绕点A按逆时针方向旋转得到△AB′C′，我们应获知对应线段相等，对应角相等，旋转角相等，即AB=AB′，∠C=∠C′。因此，求∠C′的度数就是求∠C的度数。问题就转化为在△ABC中，求解∠C的大小。

解：∵△ABC绕点A旋转得到△AB′C′，

∴AB=AB′，∠C′=∠C，

∴∠AB′B=∠B。

又∵AB′=CB′，

∴∠B′AC=∠C。

设∠C=x，则∠B′AC=∠C=x，

又∵∠AB′B是△AB′C的外角，

∴∠AB′B=∠B′AC+∠C=2x，

∴∠B=∠AB′B=2x。

∵∠B+∠C+∠BAC=180°，

∴2x+x+108°=180°。

∴x=24°，

∴∠C′=∠C=24°。