高中数学教学中的数学文化融入
——以定积分的微元法为例
韩新方,范雅婷,黄柏梅,刘孟锌,马 丽*
(1.海南师范大学 数学与统计学院,海南 海口 571158;2.数据科学与智慧教育教育部重点实验室 海南师范大学,海南 海口 571158;3.藤县中学,广西 梧州 543300;4.达州天立学校,四川 达州 635000)
极限理论是现代微积分学的基础,对于高中阶段的学生来说该内容过于丰富且难以理解。在高中阶段讲解定积分的概念时,不可避免要用到极限理论或思想,使得定积分的概念变得晦涩难懂,导致定积分应用等变成无源之水的套路或模式化,使学生产生不严谨的困惑和陷入不知对错的窘境。为避免“以未知讲新知”的不伦循环及数学学习中的不严谨,本文提出在高中阶段讲解定积分时强化微元法教学,在学生简单了解定积分定义后,用微元法来代替定积分严格定义,给出适用定积分计算的3个前提条件以及应用的3个基本步骤。本文从定积分的思想和微元法入手,给出若干经典几何问题建模的前提和具体步骤,近似严格地证明立体几何中圆的面积、球的体积等常见的公式,旨在培养学生具备一般到特殊的哲学观点,提高其抽象到具体的数学思维能力和严谨的数学逻辑推理能力,在数学课堂教学中渗透数学文化。
基于《普通高中数学课程标准(2017 年版)》,现代数学中有关微积分的基本知识[1-6]引入到了初等数学中,尤其是关于函数导数、定积分及其应用方面的内容,并日益被一些中学教师和学者所关注并研究。在高中阶段讲解定积分的概念时,通常通过求曲边梯形面积和变速直线运动路程的过程得到“分割、近似、求和、取极限”4个步骤,然后将其归结为一个特定形式和(黎曼和)的极限,进而得到定积分。这样处理比较严谨,符合现代数学的公理化体系,但太精细反而显得繁琐,而且学生并没有学习极限理论的相关知识,如此用未知的极限知识来讲解定积分会使得学生在学习定积分的时候存在不少的困难。因此,基于作者的教学实践和之前的讲究积累[7-8],本文提出在高中阶段淡化定积分的定义,达到知道“是什么”的程度即可。“怎么做”这一环节引入微元法,强调微元法中“以直代曲,以常代变”的思想,讲授适用定积分模型的前提条件以及写出定积分的基本步骤。这样既可以避免未知内容的循环论证,又可以明晰定积分应用的具体操作步骤或流程,保证数学知识的逻辑性和相对严谨性,同时也减少学生的学习困惑,提高了学生解决问题的建模能力。
利用定积分证明高中阶段(立体)几何中的基本公式是定积分的一个重要应用。对于这部分内容,本文阐述并利用微元法,期望使学生体会定积分中分割、近似求和的思想。基于此,本文选取了几组特殊的平面和立体图形进行微元法求面积或体积,分析各公式之间的联系,并探究平面及立体几何中3 个常见基本量(平面几何图形周长、面积及立体几何图形的体积)。最后指出针对学有余力的学生可以探讨微元法求平面曲线的曲线长,增加该部分内容的创造性、高阶性和挑战度。
1 微元法
从某种意义上来说,微元法是由定积分定义中“精简”出来的一种方法。它在一定程度上避开了定义中“取极限”的步骤和积分可积的必要条件(十分基础且必要,但对大部分中学师生来说确实难懂),避免循环论证发生,但是它并没有解释为什么可以将和式转化为定积分,因此微元法是具有相对的严谨性。但鉴于中学生的年龄和思维特征,使得学生学习这部分内容应更加注重应用,因此在学生简单了解定积分的定义并掌握了“精简”的微元法后,应该让学生明确微元法的适用条件以及具体的操作流程。
1.1 微元法的适用条件
定积分的应用中,如果某一实际问题中的所求量U符合下列条件[9-10],
(i)U是与某个变量(比如x)的变化区间[a,b]有关的量;
(ii)U在变化区间[a,b]上具有可加性,即如果把区间[a,b]分成许多小区间,则U相应地分成许多部分量,而U等于所有部分量之和;
(iii)根据以直代曲的思想,部分量ΔUi的近似值可以表示为f(ξi)ΔXi,
那么就可以用定积分来表达U。
1.2 微元法的具体操作步骤
写出U的积分表达式的步骤如下:
(i)根据具体问题,选定一个合适的积分变量(比如x),并确定它的变化区间为[a,b];
(ii)把区间[a,b]分割成无数个小区间,取其中任一小区间并记作[x,x+ dx],求出这个小区间的部分量ΔU相应的近似值。若ΔU能近似地表示成[a,b]上的一个连续函数在x处的值f(x)与dx的乘积,且ΔU与f(x)dx近似相等,就称f(x)dx为变量U的微元且记作dU,即dU=f(x)dx;

上述方法通常称为微元法,是一种重要的数学方法,同时也是定积分“以直代曲”思想的具体体现,因此寻求实际问题中的“微元”是利用积分解决实际问题的关键一步。
2 举例演示、化抽象为具体
在系统地讲解微元法之后,结合以下具体例子向学生演示微元法的具体操作步骤。这里选取椭圆和圆的面积和椭球的体积公式以及它们的特殊形式举例说明,目的是使学生进一步认识应用微元法的操作规范,并加深对一些特殊图形的面积以及体积公式的理解。
2.1 圆面积公式


图1 微元法求椭圆的面积Figure 1 The area of a ellipese by infinitesimal method
(1)判断是否符合微元法的应用条件:
(i)所求量S椭是与变量x的变化区间[ -a,a]有关的量;
(ii)S椭在变化区间[ -a,a]具有可加性,也就是说把区间[ -a,a]进行分割得到多个小区间,相应的S椭被分成多个部分量,则有S椭等于所有部分量之和;
(iii)取S椭其中任一小区间[x,x+ dx],则对应部分量ΔS椭的近似值为ydx。
因此,可以运用微元法求椭圆面积。
(2)利用微元法计算椭圆面积

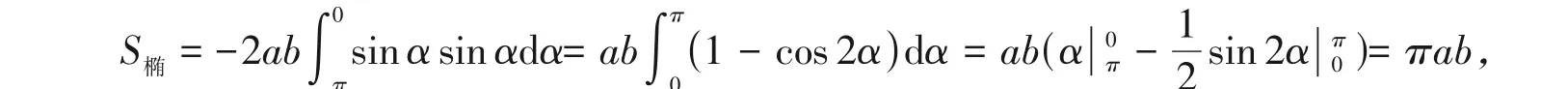
即得椭圆的面积为S椭=πab。
(3)一般到特殊的思想
已知圆是最特殊的椭圆,当a=b=r时椭圆的面积公式转化为圆的面积公式πr2。
2.2 圆柱体积和圆锥体积公式
如图2所示,圆柱的体积V柱是与圆柱的高H的变化区间有关的量,同时V柱在该变化区间具有可加性,即把该区间分割成无数个小区间,得到V柱的部分量ΔV柱(相当于把圆柱分割成无数个半径为r的小圆片),则圆柱的体积等于这些部分量的总和。其中ΔV柱的近似值可以表示成πr2dh(其中dh为分割后任意小区间的长度)。则所求量V柱满足微元法的应用条件,下面应用微元法计算圆柱的体积。


图2 微元法求圆柱体的体积Figure 2 The volume of a cylinder by infinitesimal method
在高中阶段,通过实验知道圆柱的体积是等底等高圆锥体积的三倍,但是这个结论是通过实验得出的,缺乏严谨的论证。在得出圆柱体的体积公式后,仿照圆柱体积的求法引导学生思考如何利用微元法来计算出圆锥体积。


图3 微元法求圆锥体的体积Figure 3 The volume of a cone by infinitesimal method
至此,得到圆锥体积严谨的证明。从中可以发现同规格圆柱与圆锥的体积比是3∶1。
2.3 球体体积公式
如图4所示,椭球体的体积V椭是与x的变化区间有关的量且在变化区间上具有可加性,即把该区间分割成无数个小区间,得到V椭的部分量△V椭(相当于把椭球体用垂直于x轴的平面分割成无数个小椭圆片),椭球体的体积等于这些部分量的总和,则所求量V椭符合运用微元法的条件。

图4 微元法求圆锥体的体积Figure 4 The volume of a ellipsoid by infinitesimal method
下面应用微元法计算椭球体的体积。
将x看作是积分变量,它的变化区间为[ -a,a],任取一小区间记作[x,x+ dx],在每个小区间上椭球体体积的部分量△V椭的近似值为S椭dx。其中,所截得椭圆的表达式如下:
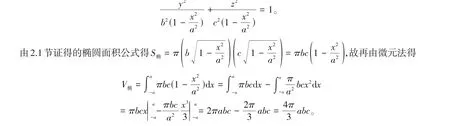
因此,椭球的体积为

此外,在证明一般图形的面积及体积公式后,还可以借助微元法向学生介绍如何计算平面曲线的长度,在“不可度量”到“可计算”的过程中感受微积分中“以直代曲”的思想并领略数学知识的魅力。这一部分内容对于提升学生数学思维的逻辑性和严谨性有重要作用,但对学生的基础要求较高,建议教师适当引导,体现数学知识的延展性及课堂的高阶性、创造性和挑战度。
3 教学建议与总结
本文意在通过讲解微元法来推广定积分的应用在高中阶段的普及,使得更多中学生感受到数学严谨性并提高其学以致用的思维能力和建模能力。由于学生的年龄特征和思维水平的局限,中学生仅适用于“相对严谨”的证明并注重应用。文中展示了3组几何公式的证明,让学生明确微元法的适用条件以及具体的操作流程,让学生从实际运用的层面体会其依据。通过分析几组公式的关系,也让学生体会到由一般到特殊的哲学思想,感受数学区别于其他学科的逻辑性和严谨性,使高中数学课堂融入整体到部分、特殊到一般、追求严谨和真理的思政元素,富有数学文化张力。

