一种基于节点路径信息相似性的预测方法

黄寿孟

（1.三亚学院 信息与智能工程学院，海南 三亚 572022；2.三亚学院 陈国良院士团队创新中心，海南 三亚 572022）

许多现实世界的复杂系统可以通过复杂网络来表示，其节点表示实体，链路表示节点之间的交互[1]。因此复杂网络被人们广泛研究与应用，其中研究复杂网络的链路预测是学者们热点问题之一，它的研究目标是估计两个尚未连接的节点之间存在链路的可能性[2]。目前，许多链路预测算法关注的都是基于节点相似性的思想[3]，利用节点的基本属性定义节点相似性，也就是说如果两个节点具有许多共同的拓扑特征，那么它们就被认为是相似的[4]。比如共同邻居算法[5]、Adamic Adar[6]、Jaccard系数[7]等局部相似度量算法可以非常有效地计算，并在许多情况下都有良好的性能；还有全局度量算法[8-9]、基于本地路径信息算法[10]都有良好Katz指数、通勤时间、节点信息的预测性能。文献[11]针对加权网络综合考虑网络中边的聚类和扩散特性提出基于链接拓扑权重的含权预测指标的预测方法。文献[12]提出一种基于社团节点相关性的链路预测算法，把节点对扩展到二阶局部社团获取更多的网络结构信息。文献[13]根据复杂网络样本邻接矩阵化处理以及采用AdaBoost 算法进行分类训练获取权重投票预测结果。文献[14]设计开发了结合网络拓扑特征、基本特征和附加特征的TNTlink模型，并结合物理学和计算机科学的领域知识，利用深度神经网络将这些特征集成到一个深度学习框架中从而解决链路预测问题。为了优化现有的基于路径预测方法，本文提出了两个节点u和v之间的新相似性索引，该索引是根据距离u和v固定距离内的节点的局部信息计算得出的。换句话说，索引信息不仅包含了直接连接到u与v的节点，还合并了位于u到v的所有可能长度较小的路径上的节点信息，最后比较两个使用最广泛的相似性指标，Adamic Adar和Katz Index的性能。

1 相关工作

网络G=(V,E)由节点的有限非空集合V和无序顶点对（称为链接）的有限集合E组成。网络可以是有向的（在每个边缘都分配有方向的地方），也可以是无向的（没有为边缘分配任何方向的地方）。本文只考虑无向简单网络，其中不允许多个链接和自环。顶点的度数v∈V是与v相连的邻居数。网络G=(V,E)中的行走w是一系列交替的顶点和边v0,e1,v1,e2,v2,…,ek,vk。其中vi∈V和ei=(vi-1,vi)。该行走具有长度k，其定义为行走中的顶点数。无向简单网络G=(V,E)的邻接矩阵类型是|V| × |V|。如果u和v有链接，则邻接矩阵（u，v）值为1，否则为0。邻接矩阵(A k)uv的第k次幂表示行走的次数，即从u到v的链接路径的长度为k。目前常用的本地和准本地/全局链接预测方法有：

1.1 公共邻居(CN）

如果两个节点存在许多公共邻居，则它们最有可能具有链接，用这种方法计算两个节点的公共邻居数[5]，其计算公式为

CN算法在许多情况下是评估其他方法性能的基准，CN也可以表示为CN(u,v) =(A2)uv，其中A是网络的邻接矩阵。

1.2 Adamic Adar（AA）

该算法目标是在通过为较少联系的邻居分配更多权重来提高普通邻居的准确性[6]，计算公式为

其中w是u和v的共同邻居。在社交网络中，此算法可以计算不受欢迎的人（朋友数量较少的人）可能更容易将一对特定的朋友彼此介绍。

1.3 Jaccard（JC）

Jaccard算法是从两个节点的公共邻居计算出的另一种相似性度量[7]，它定义为

JC的值可以解释为节点u和v的公共邻居的概率。

1.4 Katz

该算法基于整个网络的拓扑考虑节点对之间所有路径的集合[10]。路径的长度会以指数方式衰减，从而为较短的路径赋予更大的权重，它计算公式为

其中0 <β< 1是控制不同长度路径的权重的参数。β的值非常小将导致惩罚较长长度的路径，并且在这种情况下将度量减小为CN。注意，相似度矩阵S也可以计算为(I-βA)-1-I，其中，I表示大小为|V|×|V|的单位矩阵。

1.5 局部路径（LP）

为了在准确性和复杂性之间取得良好的平衡，考虑较短长度的局部路径的LP算法[15]，计算公式为

其中A是网络的邻接矩阵。与Katz 算法一样，β设置为较小的值，以便较短的路径获得更大的权重。请注意，如果β= 0，则该算法会退化为公共邻居。实际上，由于其计算较复杂，该度量通常在L = 3时使用，从而将其减小为LP(u,v) =A2+βA3。

1.6 优先联系PA

该算法表示在社交网络中有很多朋友的用户将来倾向于获得更多的联系[16-19]，其计算公式为

2 预测模型

2.1 设计背景

基于相似度的链接预测方法通常取决于网络的拓扑结构，这种方法的目的是基于节点的本地连接结构预测一对节点之间的丢失链接。本地链路预测方法使用两个节点的直接邻居的节点信息来预测它们之间的链接。例如，AA算法将较高的权重分配给程度较小的公共邻居。直觉是，度数较小的公共邻居在预测两个节点之间的链接时更为重要。虽然局部相似性算法仅考虑直接连接到查询节点的那些节点，但是全局方法（例如Katz算法和LP算法）考虑整个网络的拓扑。但是全局方法不考虑连接节点的程度。因此需要一种可以同时利用局部和全局相似性指标来测量相似性的链路预测方法。

2.2 PSI预测方法

若未加权网络G=(V,E)存在(u,v) ∈E'，如何预测两个节点u和v之间的链接。为了估计节点u和v之间潜在连接的可能性，考虑到网络中所有与节点u和v处于固定距离内的节点，笔者提出一种相似性指数（简称为PSI）计算方法。

定义1 若Γk(u)代表与节点u的最短距离为k的所有节点的集合，即节点u和v之间的相似性指数PSI(u,v)定义为

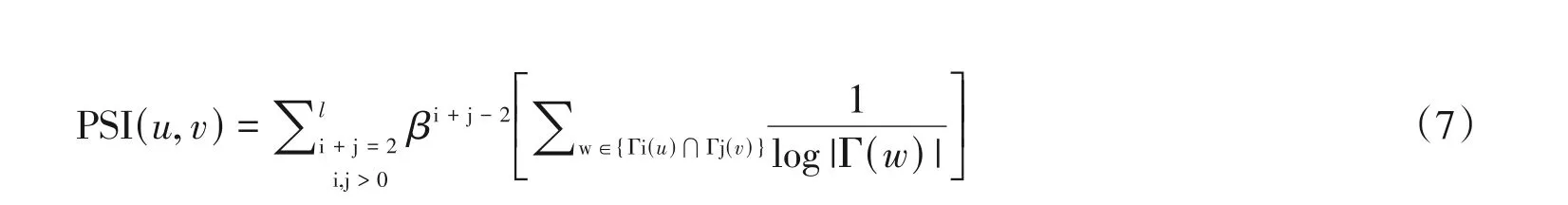
其中β是权重系数，若距离大于1的节点的权重较小，则L是在计算PSI(u,v)时考虑的最长路径的长度。此方法结合了Adamic Adar 和LP 算法的优点，考虑水平范围比AA 宽的本地路径（AA 仅考虑两个节点的直接邻居），同时也考虑了每个节点的程度（LP算法仅计算本地路径，而忽略程度）。

由于网络中一对可达节点之间的最短距离始终是唯一的，因此建议在相似性指数PSI计算中每个节点仅被考虑一次，从而得出PSI的等效定义。

定义2 两个节点u和v之间的相似性指数PSI(u,v)定义为

其中δ(u,v)表示节点u和v之间的最短距离。

2.3 PSI算法

对于L= 2，PSI简化为AA，LP指数简化为CN。因此假设L> 2，PSI(u,v)的值计算如下:

若节点u和v未连接，首先确定节点u和v的公共邻居，并通过取其度的对数的倒数来计算其分数。该分数被添加到相似性指数PSI(u,v)。接着计算连接到两个节点u和v中的一个但距另一个节点的最短路径恰好是两个的节点。它们的分数是以类似的方式计算的，即取其度的对数的倒数。但是它们在预测得分的计算中分配的权重较小。这是通过将他们的分数乘以β(0 <β< 1)来完成的，然后将其值添加到PSI(u,v)。该过程一直持续到计算出与节点u和v的距离小于或等于L的所有节点的分数。

注意这时L的最大值可以是2d，其中d是网络的直径，其定义为网络中所有节点对之间最短路径中的路径最大长度。

下面是计算相似性指数PSI的算法过程，其中GT表示用于训练学习的网络集合，ET表示用于训练学习的邻接节点对集合：

1：输入：网络GT=(V,ET)，具有邻接矩阵A，距离长度L值和权重参数β。

影响消费者购买叶类蔬菜行为关键因素分析………………………………………………………… 张 标，徐 娜，张领先（128）

2：输出：相似度得分矩阵S。

3：s←0

（将相似矩阵初始化为0）

4：δ←All Pair Shortest Paths(GT)

（计算最短路径）

5：for (u,v) ∈EETdo

6：forw∈V{u,v}do

8：ifd≤1 then

9：PSI(u,v) ←PSI(u,v) +βd-2(log|w|)-1（更新相似性得分）

10：end if

11：end for

12：end for

在PSI算法中，接受网络GT的邻接矩阵作为输入，该矩阵是通过去除EP中的链接而获得的。它还接受权重参数β和L（L的最大值为最大路径的长度）。首先计算网络中所有节点对之间的最短路径，for循环（第5至12行）遍历所有未连接的节点对，将来可能会链接起来。通过考虑网络中所有节点的相似性得分，这些节点从两个节点到最短路径的总和小于L，而相似性得分根据等式在第11行中更新。

3 实验结果

3.1 数据集

3.2 评估指标

为了估计预测算法的准确性，本文使用标准度量AUC精度指标[1]。如果在n个独立预测比较中，n'是缺失链接具有较高分数的次数，n''是缺失链接和不存在具有相同分数的链接的次数，则将精度AUC = (n' +0.5n'')/n如果所有链接分数均根据独立的概率相同分布随机生成，则预测算法的AUC精度指标应约为0.5。因此，若AUC > 0.5，即表示该算法的预测性能效果好，且AUC值越接近1表示预测效果越好。

3.3 结果

本文将数据集网络的链路集合E随机分为两组，即训练集ET和测试集EP。训练集包含90%的链接，而其余10%的链接用于测试目的，使用相同的集合ET和EP来评估各种预测方法的性能。同时在PSI，Katz 和LP算法中参数值β= 0.005，L= 3，每个数据集进行100次实验，从而得到每个算法平均精度AUC值见表2。

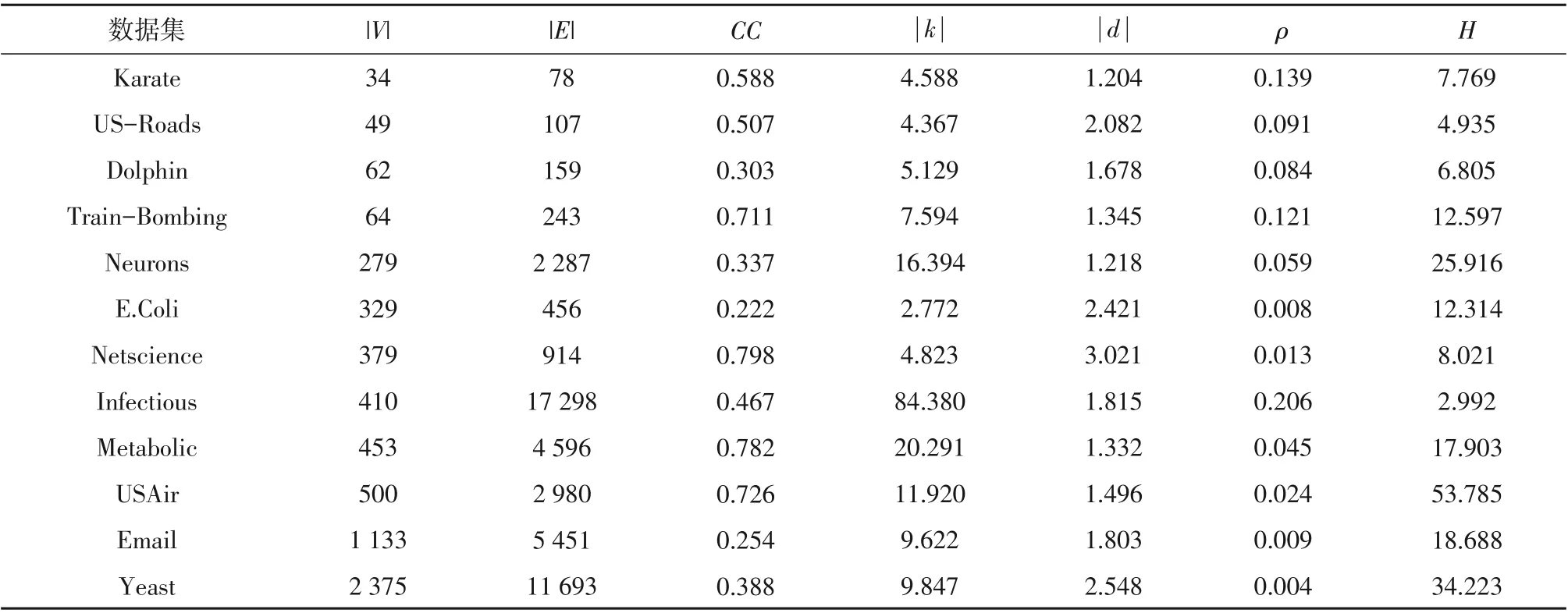
表1 数据集网络的拓扑特性Table 1 Topological characteristics of the data set network

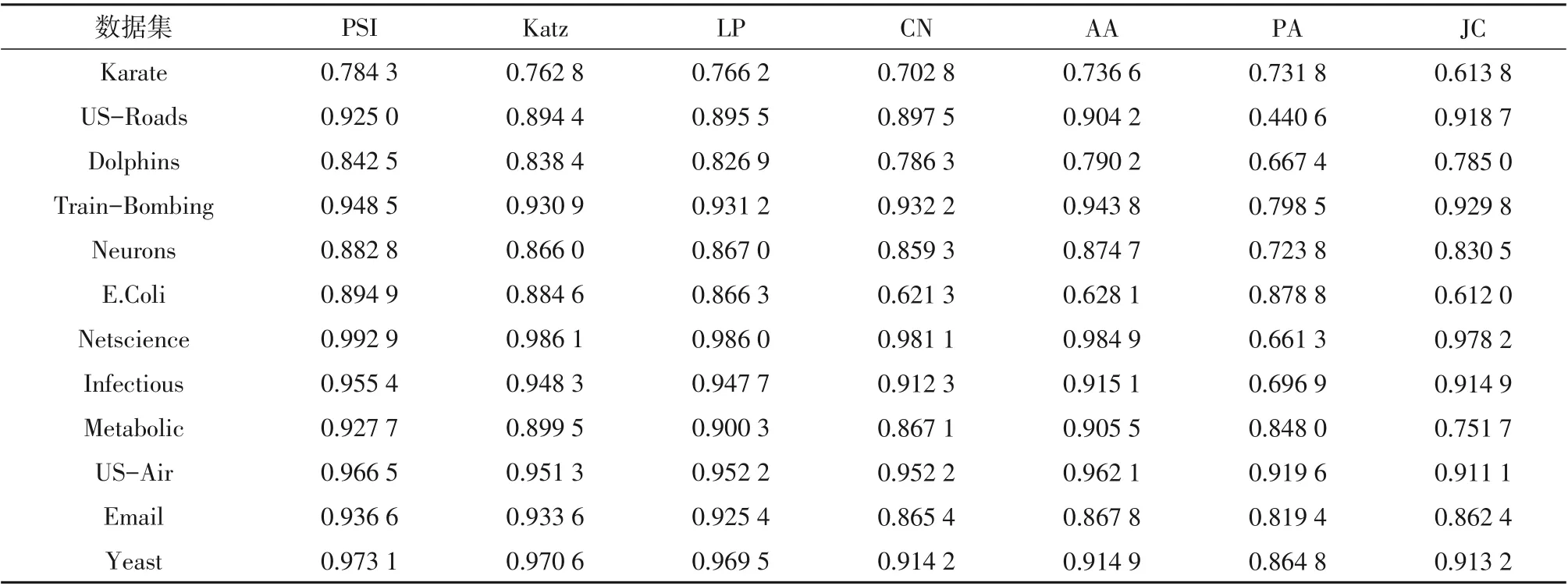
表2 各算法在不同数据集下的预测精度AUCTable 2 AUC for each algorithm under different data sets

从表2中明显得出，PSI算法在不同的数据集中的预测精度AUC 值均高于其他算法在同一数据集上所得到的AUC值，预测效果较好，其通过合并有关可达节点的信息使预测算法的准确性大大提高。

4 结论

链路预测是复杂网络分析中最重要和最具挑战性的领域之一。链路预测算法的目标是基于网络中的现有链路来估计丢失链路的可能性。本文设计了一种基于本地路径索引的链接预测方法，结合有关路径上的节点信息预测网络中两个节点之间存在链路的可能性。与基于本地路径的频率来预测丢失链接的本地路径索引不同，本文提出的方法合并了有关路径上的节点信息，最后利用真实数据集进行实验分析，证明该方法比原有的方法具有更高的准确性。