基于图的覆盖决策信息系统属性约简新算法

张 杰，张燕兰*，林艺东

（1.闽南师范大学 计算机学院，福建 漳州 363000；2.厦门大学 数学科学学院，福建 厦门 361005）

由Pawlak[1]提出的粗糙集理论是一种处理不确定信息的重要工具，在数据挖掘、机器学习和知识发现等领域有重要的应用。在粗糙集理论中，数据通常由信息系统来表示，并且由一组特征来描述。然而，这些特征中有许多是冗余的，这使得分类过程更加困难。因此，通过选择相关的特征来减少冗余的特征的数量是很有必要的。属性约简的主要目的是去除数据集中的冗余信息，这不仅可以减少学习算法的运行时间，在某些情况下还可以提供更好的分类精度。

在经典的粗糙集中，很多学者已对属性约简作了深入的研究[2-4]并取得了重要的结果。例如，钱宇华等提出了4种寻找属性约简的加速算法[5]。然而，基于经典Pawlak粗糙集模型的属性约简方法只适用于离散型数据，并不能直接应用于连续型数据。换句话说，属性约简之前需要对连续型数据进行离散化，而这会造成信息损失和丢失[6]。为此，很多学者提出了覆盖粗糙集、相似关系粗糙集和邻域粗糙集等广义粗糙集模型[7-13]。Chen等提出了一种基于覆盖粗糙集模型的属性约简方法[14]，此方法可以用来处理数值型数据，而且不需要对数值型数据离散化，只需转化为一个覆盖决策系统即可。在此基础上，Chen等又提出了另一种基于覆盖粗糙集模型的属性约简方法[14]，但是，该算法非常耗时。为了克服这个缺点，Wang等简化了文献[14]中辨识矩阵的构造，提出了一种更有效的寻找属性约简的CDA算法[15]。CDA算法可以有效地处理中等规模的数据集，然而，CDA算法的计算复杂度随着样本和属性的增加呈指数增长，且CDA算法可能会得到一个空的特征子集，因此，对于较大数据集，需要更有效的属性约简方法。于是，Chen等提出了一种基于图的覆盖决策信息系统属性约简的CDG算法[16]，结果表明CDG算法比文献[15]中CDA算法更高效。

本研究在文献[15]的基础上研究覆盖决策信息系统属性约简的问题，并在文献[16]的约简理论框架下研究基于图的覆盖信息系统属性约简的新方法，采用的策略是：首先计算覆盖决策信息系统的辨识集，进而得到一个超图的关联矩阵；然后，基于贪心法求该超图的极小顶点覆盖；最后，通过连续型数据实验分析得知新算法的时间复杂度为O(|U||A|)，其中|U|与|A|的含义分别是论域的大小、属性集的大小，这比CDG算法的时间复杂度O(|U|2|A|)更低。

1 预备知识

1.1 覆盖决策信息系统的属性约简

在本节中，先介绍覆盖粗糙集和图论的几个基本概念。称S=(U,A)是一个信息系统，其中U和A分别是非空有限论域和属性集。对于任意属性a∈A，称a:U→Va是信息函数，其中Va称为属性a的值域。决策信息系统的形式为S=(U,A,{d})，其中(U,A)是一个信息系统，A是条件属性集，d:U→Vd是决策属性，且d∉A。

众所周知，经典粗糙集只能用于处理离散型数据。然而，在许多实际的情况中经常要面临连续型数据的情况。现在回顾相关文献中处理连续型数据的属性约简方法[14-15，17]。

定义1[17]设U为论域，C是U的子集族，如果C中不含空集，且∪C=U，则称C为U的一个覆盖。

定义2[14]设C={K1,K2,...,Kn}为U的一个覆盖，对于每一个x∈U，令Cx=∩{Kj|Kj∈C,x∈Kj}，则Cov(C) ={Cx|x∈U}也是U的一个覆盖，称Cov(C)为C诱导的覆盖。设Δ ={Ci|i= 1,2,…,m}为U的一族覆盖，∀x∈U，记Δx=∩{(Ci)x|(Ci)x∈Cov(Ci) ,i= 1,2,…,m}，那么Cov(Δ) ={Δx|x∈U}也是U的一个覆盖，称Cov(Δ)为Δ的诱导覆盖。∀X⊆U，X相对于Δ的上、下近似算子定义如下：

通常，对每个数值型属性a∈A，可以定义每个样本x∈U的邻域。Na(x,ε) ={y∈U|d(x,y)ε}，其中d( ⋅, ⋅)是一个距离函数，ε是指定的阈值。通常，d(x,y) =|a(x) -a(y)|。显然，Na={Na(x,ε)|x∈U}是U的一个覆盖，Δ ={Na|a∈A}是U的一个覆盖族。因此，可以获得一个覆盖决策信息系统S=(U,Δ,{d})。

例1 设S=(U,A,{d})为一个由连续型属性组成的决策信息系统（见表1），其中U={x1,x2,x3,x4,x5}，A={a1,a2,a3,a4}，d是决策属性。

表1 数值型数据表Table 1 Table of numerical data

令阈值ε= 0.20，可以获得以下覆盖决策信息系统S=(U,Δ,{d}):

另外，U/d={{x1,x3},{x2,x4,x5}}，记D1={x1,x3}，D2={x2,x4,x5}。

例2（续例1） 覆盖决策信息系统S的辨识矩阵如表2所示。为简单起见，我们对集合使用无分隔符形式，例如，用C1C2C4表示{C1,C2,C4}。

表2 覆盖决策信息系统S的辨识矩阵Table 2 Discernibility matrix of S

在覆盖决策信息系统S=(U,Δ,{d})中，覆盖C1,C2,…,Cm分别对应于m个布尔变量C*1,C*2,…,C*m，则定义辨识函数fS如下:

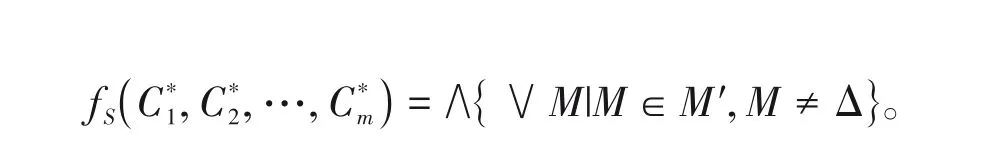
这种简化析取形式的每一个合取式被称为主蕴涵[18]。Wang等通过析取和合取运算证明了覆盖决策信息系统的约简计算可以转化为布尔函数的主蕴涵的计算[18]。

表3 点的邻域Table 3 The neighborhood of a point

1.2 超图的顶点覆盖

超图是传统图的泛化，超图里的边可以连接任意数量的顶点。一般，超图H可以表示为(V,ε)，其中V是所有顶点元素的集合，ε是V的非空子集族，ε的元素被称为超边或者边，用E表示。而超图H的顶点覆盖K是一个集合K⊆V，且K与H的每条边交非空。换句话说，顶点覆盖是一组覆盖所有边的顶点集合。如果K的任意子集均不是顶点覆盖，则顶点覆盖K是极小的。极小顶点覆盖是顶点数目最少的顶点覆盖。超图H的所有极小顶点覆盖的集合用T(H)表示。与粗糙集中的属性约简方法相似，超图的所有极小顶点覆盖也可以通过逻辑表达式得到。

2 基于图的覆盖决策信息系统的属性约简

从引理1和引理2可以看出，覆盖决策信息系统的属性约简与超图的极小顶点覆盖之间存在联系。在本节中，我们首先介绍由覆盖决策信息系统诱导出的超图，然后讨论导出超图的极小顶点覆盖与覆盖决策信息系统属性约简之间的关系，最后，提出一种基于图的覆盖决策信息系统属性约简的近似算法。

2.1 覆盖决策信息系统中的超图

定义5[16]设S=(U,Δ,{d})为覆盖决策信息系统，其中Δ ={C1,C2,…,Cm}，Μ′是S的可分辨识集，M*={M∈M′|M≠Δ}。令V= Δ,ε=M*，称H=(V,ε)为S的诱导图。

定义5是在文献[3]的基础上给出的，仅适用于分类数据。回想一下，超图是传统图的泛化。覆盖决策信息系统的诱导图H可能是一个传统的图，但在大多数情况下，它是一个超图。因此，如果不存在歧义，我们就把定义5中的诱导图称为超图。

例5（续例1） 易知：M*={{C2,C4},{C1,C2,C4},{C1,C3,C4}}。S诱导的超图H=(V,ε)为：ε={{C2,C4},{C1,C2,C4},{C1,C3,C4}}，V={C1,C2,C3,C4}。

通过引理1、引理2以及定义5，可得到下面的结果。

定理1[16]设H=(V,ε)为覆盖决策信息系统S诱导的一个超图，则Red(S)=T(H)。

定理1给出一个覆盖决策信息系统属性约简的图模型。可以看到，求一个覆盖决策信息系统的所有约简可以看作是求一个超图极小顶点覆盖集，这为我们提供了获取覆盖决策信息系统属性约简的新方法。

例6（续例5） 知：Re d(S) ={{C4},{C1,C2},{C2,C3}}。从例4 诱导的超图所有极小顶点覆盖集合为：T(H)={{C4},{C1,C2},{C2,C3}}。

因此，有Red(S) =T(H)。

2.2 覆盖决策信息系统的属性约简算法

在实际应用中，没有必要找出覆盖决策信息系统的所有约简，只需要找到一个约简。此外，相较于效率来说，找到约简是否为最小并不是很重要。在大多数文献中，粗糙集属性约简算法得到的是次优约简。在本小节中，将给出一种新的基于图的覆盖决策系统属性约简的近似算法，其中生成覆盖决策表的超图是构造上述约简算法的关键步骤之一。接下来将用关联矩阵的简单表示设计一个快捷计算超图的算法。超图H=(V,ε)的关联矩阵是一个m×n的矩阵MH=(mij)m×n，其中|ε| =m，|V| =n。若边Ei和顶点vj是关联的，则mij= 1；否则，mij= 0。

例7（续例4） 例4 所示的超图关联矩阵是一个由3 行(对应于3 条边E1～E3)和4 列(对应于4 个顶点V1～V4)组成的矩阵，见表4。

表4 例4中超图H的关联矩阵Table 4 Incidence matrix of hypergraph H of example 4

下面给出生成覆盖决策信息系统的超图的算法：

算法1 生成覆盖决策信息系统的超图（CDG1）

输入：一个决策信息系统S=(U,Δ,{d})和ε；//ε是一个阈值；

输出：超图MH。

1.forx∈Udo

2.if d(x)≠d(y)then

3.M'(x,y) ={|data - title(data)| >ε}//title(data)对原数据集的每一行复制并平铺

4.MH G(M'(x,y))

5.end if

6.end for

7.删除MH多余的行，且删除和等于0或|A|的那一行。

由于CDG1算法仅有一层循环，其计算的时间复杂度为O(|U||A|)，相较于文献[16]中算法1的时间复杂度O(|U|2|A|)更低。值得注意的是由算法1生成的辨识集M' ={M'(x,y)|x,y∈U}与定义4中定义的辨识集不一样。但是，M′比定义4中M更容易实现，因为对于任何覆盖C∈Δ都不需要再计算Cx。事实上，它们有如下关系：

命题2[16]令H=(V,ε)和H' =(V,ε')是两个超图，满足任何E∈ε，E' ∈ε'，则E' ⊆E。如果K⊆V是H'的极小顶点覆盖，那么K也是H的一个顶点覆盖。

根据命题1和2，得到以下结果：

定理2[16]设S=(U,A,{d})为决策信息系统。M'和M分别是由算法1和定义4生成的两个辨识集。如果P⊆Δ是M'的一个约简，则POSP(d)= POSΔ(d)。

定理2为我们构造新的属性约简算法提供了基础。结合定理1可知，由算法1导出超图的极小顶点覆盖可以得到一个决策表的近似约简。根据上述结果，我们设计一种新的覆盖决策信息系统属性约简近似算法2。

算法2 基于图的覆盖决策信息系统的约简算法（CDG2）

输入：一个决策信息系统S=(U,A∪{d})和ε；

输出：一个约简Red。

1.生成超图MH=(V,ε)；//参见算法1

2.令Red= ∅

3.whileε≠∅do

4.v0= arg max{dMH(v)|v∈Vx}，

Red[Red,v0]；//去掉E中被Red所覆盖的边，并仍记为E

5.end while

6.if Red -{v}//能覆盖简化图G的所有边

7.Red Red -{v}

8.end if

9.输出Red。

该算法的主要思想是基于求超图极小顶点覆盖的贪心法[9，14]，步骤1～8 的时间复杂度为O(|U||A|)。因此，CDG2的时间复杂度为O(|U||A|)，比文献[16]中算法2的时间复杂度O(|U|2|A|)更低。为了验证该算法的有效性，将其与文献[16]中的CDG的算法进行了比较。比较的指标有：生成辨识集的运行时间、生成约简集的运行时间、约简的程度。

3 实验结果与分析

3.1 数据准备

所有的算法都是在Python3.6中实现的，并在装有Windows 7的个人电脑上运行，其他要素为：双核处理器，采用串行编程，CPU 主频为2.4 GHZ，睿频为3.0 GHZ，内存为10 GB。实验选用10个公开的数据集进行验证。具体的数据集描述见表5。

3.2 实验比较

表5记录了从UCI公开数据集中选取10个常见的数据集，有小样本，也有高维小样本，以检验本文算法在真实数据集上的有效性。具体实验结果如表6～8所示。

表5 实验数据集Table 5 Experimental data set

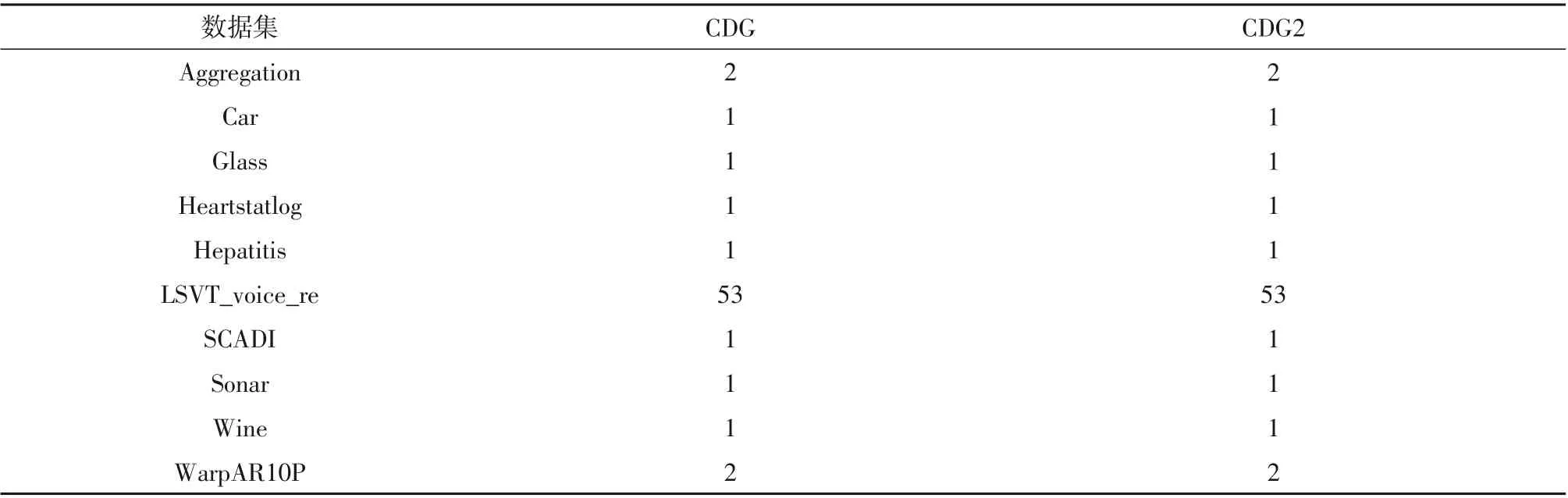
表6 约简后的属性数量Table 6 Number of attributes after reduction

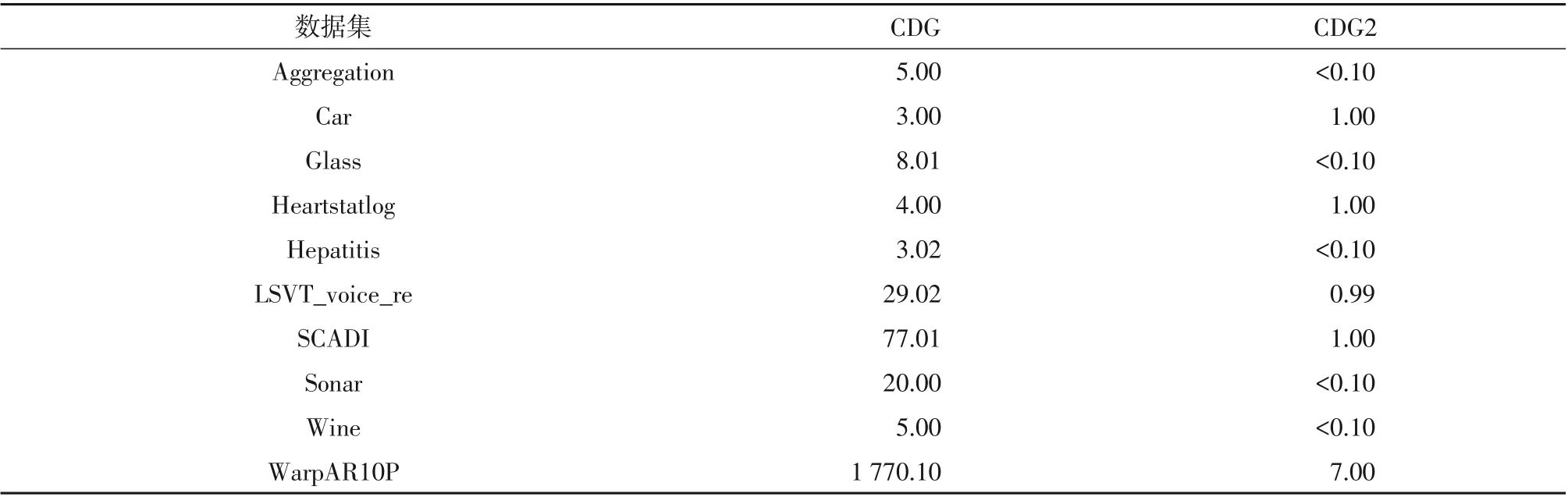
表7 辨识集的运行时间Table 7 Running time of identification data set ms

表6为CDG2算法和CDG算法对10个数据集具体的约简结果。从表中可以看出，本文提出的CDG2算法和CDG算法都可以获得极小的属性子集，CDG2算法在获得的极小属性子集的数目上也保持着优势，实际上它们均能获得一个真正的约简集。

表8为CDG2算法和CDG算法在8个数据集上产生约简集的运行时间。从表中可以看出，本研究提出的CDG2算法在Aggregation 数据集上得到约简集的时间是CDG 算法的14.24%，在Car 数据集上得到约简集的时间是CDG算法的21.23%，在Glass数据集上得到约简集的时间优势更加明显。由此可见，CDG2算法计算约简运行时间均小于CDG算法，这些数据结果进一步表明CDG2算法是一种高效的属性约简方法。综上可知，CDG2算法优于CDG算法。

表8 约简集的运行时间Table 8 Running time of reduced set ms

4 结论

属性约简是粗糙集领域重要的研究内容之一。本研究提出了一个基于图的覆盖决策信息系统属性约简的贪心算法，该算法可以直接处理数值型数据。此外，与文献[16]的CDG算法相比，CDG2算法方法更适合处理高维大数据集，同时，CDG2算法有较低的时间复杂度，并通过实例和数值型实验验证了该算法的有效性，该方法可以看作是一种局部逼近最优的特征选择策略。然而，如何进一步获得最小顶点覆盖以生成一个尽可能接近最优解的最小特征子集，这是我们后续的主要研究方向之一。