基于AHP耦合TOPSIS的铁路线路方案优选模型

杨 雪，王 龙

（1.中交铁道设计研究总院有限公司 线路站场设计处，北京 100088；2.中国铁路经济规划研究院有限公司 运输研究所，北京 100038)

0 引言

铁路线路方案比选和评价是新建铁路前期设计的一项基础性工作，不仅直接关系到项目建设工程难度、投资费用和建成后的运营成本，同时也对沿线地区的社会经济和生态环境产生重要影响。因此，对于铁路线路方案的评价和比选，是一项综合考虑各方面因素的多目标决策问题。

在铁路线路方案评价方面，国内外专家学者进行了较为深入的研究和探索，取得了丰硕的理论成果。吴小萍等[1]基于线性分配法和消去与选择转换法建立了线路方案多目标决策优选模型，以解决有限线路方案的排序问题。李远富等[2]将铁路线路方案优选视为多目标决策系统模糊优化问题，并建立了相应的模糊优化模型。罗园等[3]通过引入变权理论以弥补选线方案评价和比选工作中由于指标差异性过大而导致最后评价结果偏重于极端的情况。高康[4]应用层次分析法对敦化至白河铁路线位走向进行分析，实现了不同方案的量化比较，从而为敦化至白河铁路选线提供参考和依据。陈俊等[5]应用物元可拓理论，并结合层次分析法权重确定方法，依据优选评价等级划分标准，提出了铁路选线设计方案物元优选综合评价模型。

上述文献针对铁路线路方案评价和比选问题，采用不同的模型和算法予以解决，但均存在一定的缺陷和不足，或未能有效实现定性指标的量化，或难以消除常权赋值所引起的评价结果偏差等。铁路线路方案比选是一项复杂的多目标决策问题，对此，拟融合相关理论方法的优点，提出层次分析法(AHP)耦合逼近理想排序法(TOPSIS)的方法对铁路线路方案进行比选，从而提高线路方案评价的科学性与合理性。研究思路为：①通过对铁路选线影响因素的筛选和聚类，将线路方案评价指标归结为技术条件、经济条件、社会条件、环境条件4大类，并根据实际项目情况选择相应的评价指标。②对选取的指标采用AHP计算得出表征不同指标重要程度的权重，为最优方案的选择提供依据。③通过云模型理论对其中的定性指标进行量化处理，从而使得方案评价更具直观可比性。④考虑到对于不同线路方案，若应用统一的常权权重进行评价，将难以避免与实际要求相背离的方案“被优选”的极端情况，对基于AHP所得的常权权重进行变权处理，使得指标权重随指标取值状态不同而变化，采用TOPSIS计算各方案与理想方案贴近度，从而使得最优方案更具实际合理性。

1 基于云模型量化定性指标

对于铁路线路方案的评价，不免会选取部分定性指标纳入考量体系，例如铁路建设对地方经济的促进作用、对自然保护区的影响等，对其进行合理量化处理是确定最优方案的重要前提。而云模型即为将定性概念转换为定量数值的有效解决方法。

1.1 云模型量化定性概念的步骤

设定一个用精确数值表示的定量论域空间U以及对应该论域的定性概念C，设定量数值x∈U为模糊概念C的一次随机实现，x对C的确定度为μ(x)∈ [0，1]是一个随机数且具有稳定倾向，则在值域U上x的分布C(x)即为云，其中每一个x即为1个云滴。

通过云模型的3个数值特征来实现定性概念的定量表示，输入数值特征C(Ex，En，He)，生成N个云滴(xk，yk)，其中k= 1，2，…，N。其中，熵En表示定性概念随机性的度量，反映代表这个定性概念的云滴的离散程度，即论域空间可被定性概念接受的云滴取值范围；超熵He是熵En的熵，反映每个数值隶属这个语言值程度的凝聚性，即云滴的凝聚程度；xk为定性概念在论域空间U对应的数值；yk为属于这个语言值的程度的量度[6]。

步骤1：以En为期望、He2为方差，生成正态随机数Es。

步骤2：以Ex为期望、Es2为方差，生成正态随机数xk。

步骤4：重复步骤1到步骤3，直到产生N个云滴(xk，yk) (k= 1，2，…，N)，并取yk(k= 1，2，…，N)均值作为定性指标的量化数值。

1.2 铁路选线中定性指标的量化处理

影响铁路线路方案评价的定性指标，部分为正向指标，即影响越大，线路功能越优，比如对地方经济的促进作用、吸引货流能力等；而另有部分定性指标为负向指标，影响越大，线路功能越差，比如对城市规划的影响、对自然保护区的影响等。为便于处理，将定性指标全部定义为正向指标，并依据专家经验采用“好、较好、一般、较差、差”5个等级水平予以模糊评价，相应地，定性指标即统一划归为正向指标。由此，参考既有相关研究成果[5,7]，对定性指标的不同评价水平进行云模型表述，对应的论域U、期望Ex、熵En(取值U/6)与超熵He(取值0.02)赋值，定性指标评价水平与云模型表述的对应关系如表1所示。

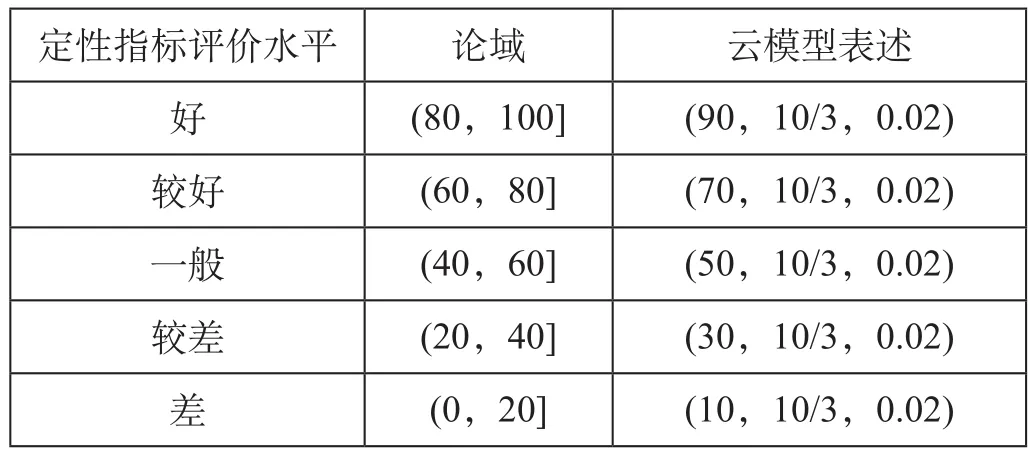
表1 定性指标评价水平与云模型表述的对应关系Tab.1 Evaluation level of qualitative indicators and corresponding relationships of cloud model expressions

2 基于AHP确定初始常权

根据对实际设计工作中铁路线路方案影响因素的总结和归纳，构建线路方案评价指标体系，共计包括4个方面，即一级指标：技术条件、经济条件、社会条件和环境条件，其中任意一级指标所包含的二级指标根据实际案例情况选取。采用AHP确定各指标的初始常权。

2.1 构造判断矩阵

标度反映决策者对同层指标相互间重要性的主观感觉。利用1-9比例标度法对同层中任意2个评价指标间的相对重要性进行量化赋值，其中，“1”表示2指标具有同等重要性，“9”表示前者相比于后者极度重要，其余中间数字表示与其值大小相对应的重要程度。另外，同层中指标rs相对于指标rt的标度为rt相对于rs的标度的倒数，由此，即可充分结合专家经验，对各层中任意2个指标的相对标度进行标定，从而构造出各层的判断矩阵B，即

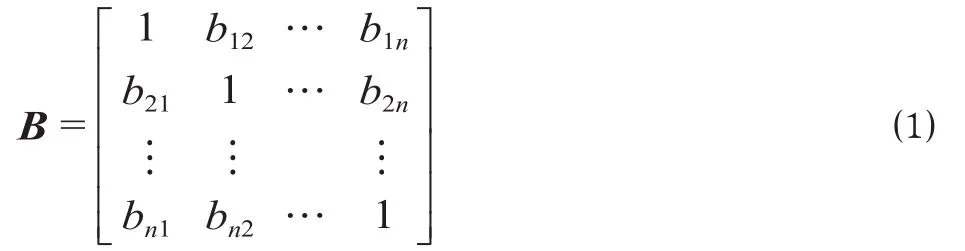
式中：n为判断矩阵阶数；bst为指标rs相对于指标rt的标度。

2.2 计算权重

对于每一层，利用方根法计算各指标的权重，计算步骤如下。

首先，计算判断矩阵第s行元素乘积的n次方根，即

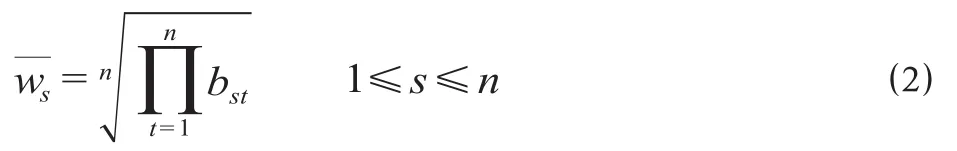
式中：ws为指标s的权重。

由公式 ⑴ 可见，判断矩阵B具有正定互反性质，则其存在唯一的最大特征根，即

式中：λmax为判断矩阵的最大特征根；W为由指标s的权重ws构成的矩阵。

2.3 一致性检验

为了规避因人为设定判断矩阵中标度值而出现的不合理性，需通过对判断矩阵进行一致性检验来进行甄别。

首先，计算判断矩阵的一致性指标，即

式中：CI为判断矩阵的一致性指标。

其次，进一步计算判断矩阵的一致性比例，即

式中：CR为判断矩阵的一致性比例；RI为平均随机一致性指标。

若CR<0.1，则表明判断矩阵满足一致性检验要求，则w= (w1，w2，…，wn)T为指标权重，否则需对判断矩阵进行修正。

3 基于TOPSIS评价线路方案

TOPSIS是一种逼近于理想解的排序法。其基本原理是通过检测评价对象与最优解、最劣解的距离来进行排序，若评价对象靠近最优解同时又最远离最劣解，即为最优。其中，最优解为其各指标值均达到各评价指标的最优值，最劣解则其各指标值均为各评价指标的最差值[8-9]。

3.1 建立初始评判矩阵

设铁路线路方案集由m个备选方案构成，每个方案均包含n个评价指标，由此构建初始评判矩阵A如公式 ⑺ 所示。

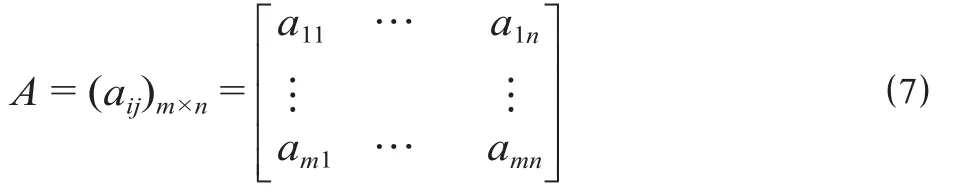
式中：aij为第i个方案的第j个评价指标，1 ≤i≤m，1 ≤j≤n。

3.2 标准化评判矩阵

由于各评价指标的数量级和单位各不相同，无法直接进行比较，因而需要对评判矩阵进行标准化处理，以使不同指标之间具有可比性和共度性。根据评价指标数值大小对线路方案评价结论的影响可将评价指标分为正向指标和负向指标2类，则正向指标和负向指标的标准化处理公式分别如公式 ⑻和公式 ⑼ 所示 。

式中：βij为标准化处理后的方案i指标j取值，1 ≤i≤m，1 ≤j≤n。

3.3 惩罚型变权处理

为避免使用常权而出现“状态失衡”，导致评价结论出现偏重于极端的情况，这里在常权基础上，通过引入变权思想实现权向量的动态调整，使得指标权重随取值状态而变化，不仅可以满足各指标的相对重要次序，也能够保证指标间的均衡性。

以常权为基础的惩罚型变权公式如下。

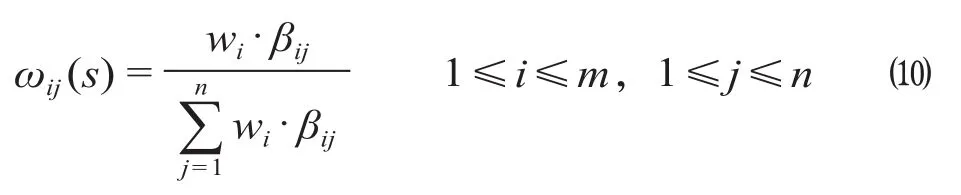
式中：ωij为方案i指标j的变权权重；wi为基于AHP 求得的指标j初始常权 ，1 ≤i≤m，1 ≤j≤n。

经变权处理后，得到加权的规范化矩阵L=(lij)m×n，即

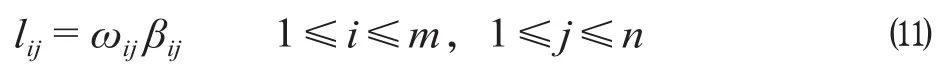
式中：lij为加权规范化后的方案i指标j取值，1 ≤i≤m，1 ≤j≤n。

3.4 计算方案贴近度

步骤 1：以加权规范化矩阵L为基础，比选各方案的第j个指标，分别计算出相应的正理想方案和负理想方案如下。

步骤2：计算各方案与正、负理想方案的距离如下。

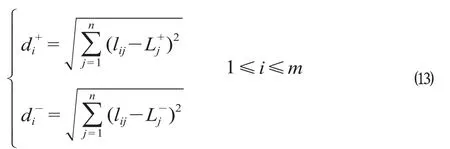
步骤 3：计算各方案与正理想方案的贴近度如下。

式中：Ei为方案i与正理想方案的贴近度，1 ≤i≤m。

Ei值越大，则表明方案i距离正理想方案越近、距离负理想方案越远，即方案越优。

4 案例分析

以上述模型为内置算法，基于Visual Studio 2010平台开发了铁路线路优选系统，下面结合新建新交口至安泽铁路实际案例对模型有效性及实际应用价值进行验证分析。

新建新交口至安泽铁路位于山西省长治市和临汾市境内，本项目建成后将成为区域内煤炭外运的重要径路，是能源大通道瓦塘至日照铁路集运系统的重要组成部分。在项目可行性研究阶段，根据区域内地形情况、既有和在建车站情况及车流方向，并结合地方政府意见，共提出3个线路方案，即西线方案、中线方案和东线方案，3个方案比较起点为和川站，比较终点为集运站。

西线方案线路起自在建永鑫铁路专用线的预留和川站，利用永鑫铁路专用线，至唐城站小里程咽喉以18号道岔引出后，与在建唐城站并行1.2 km横列设置本线到发场后向东北以2.2 km隧道绕避太岳煤焦化厂规划位置，随后跨过中唐路，后以2.3 km隧道穿山至中峪乡，之后跨过县道X643和乌木村村道后线路以短隧道穿过山脉，跨过国道G341，沿沁河西侧向北而行，至比较终点。

中线方案总体走向与西线方案总体一致，差异之处为线路自中峪站引出后跨过县道X643，之后线路以长隧道穿过山脉，局部绕避中峪煤矿首采区后跨过国道G341，沿沁河西侧向北而行，至比较终点。

东线方案线路自在建永鑫铁路专用线预留和川站引出，折向东以0.9 km，2.8 km，2.1 km隧道至沟口西侧，后转向北，以0.9 km隧道行至小南川，预留小南川站位置，之后跨越柏子河继续向北而行，至沁源县北侧，跨过国道G341到达比较终点。

3个方案的选线方案示意图如图1所示。

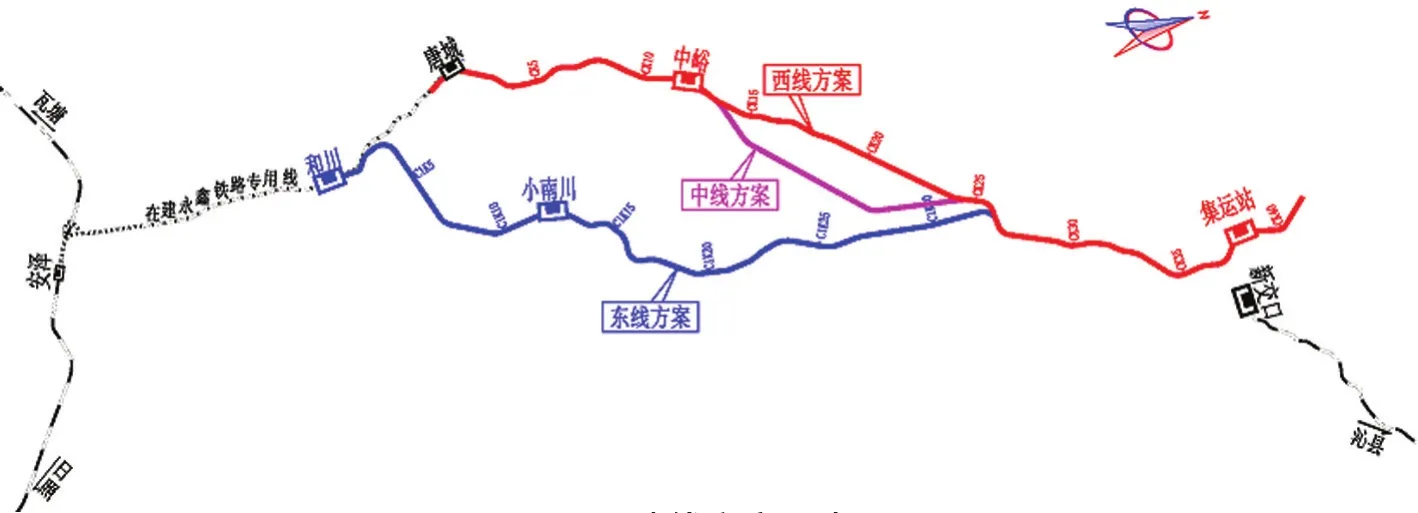
图1 选线方案示意图Fig.1 Selection schemes for railway alignment

根据新交口至安泽铁路线路方案的比选需要，将方案比选的分层指标集及其相应的定量指标数值与定性指标评价水平录入系统，线路方案指标数值及评价水平如图2所示，共计20个指标，按图2中顺序分别标记编号为C1至C20。

由图2中各线路方案的指标表现来看，3个方案各具优缺点，线路方案优缺点分析如表2所示。

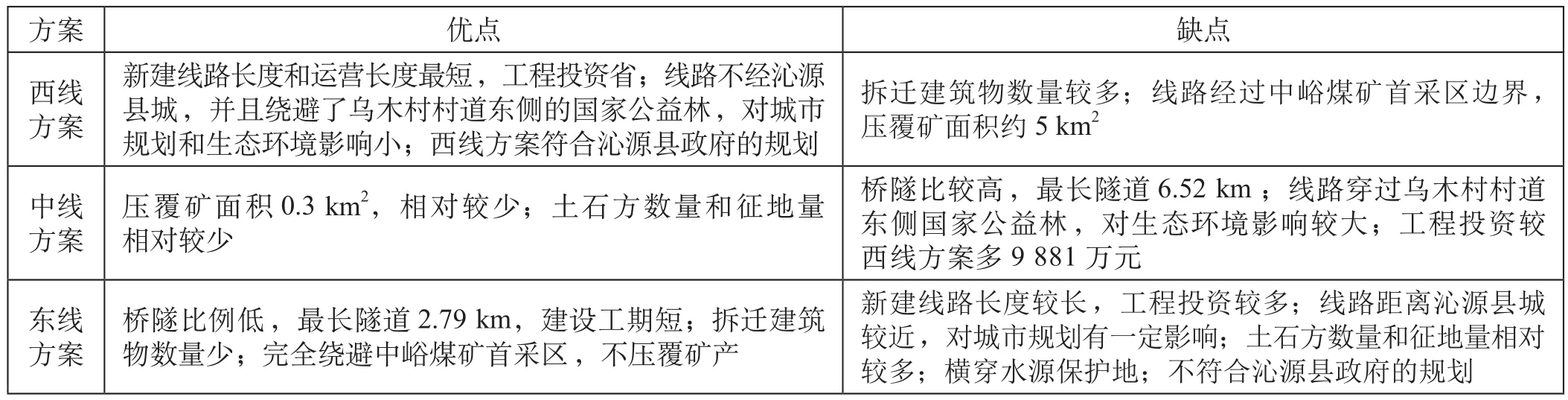
表2 线路方案优缺点分析Tab.2 Advantages and disadvantages of each railway alignment scheme

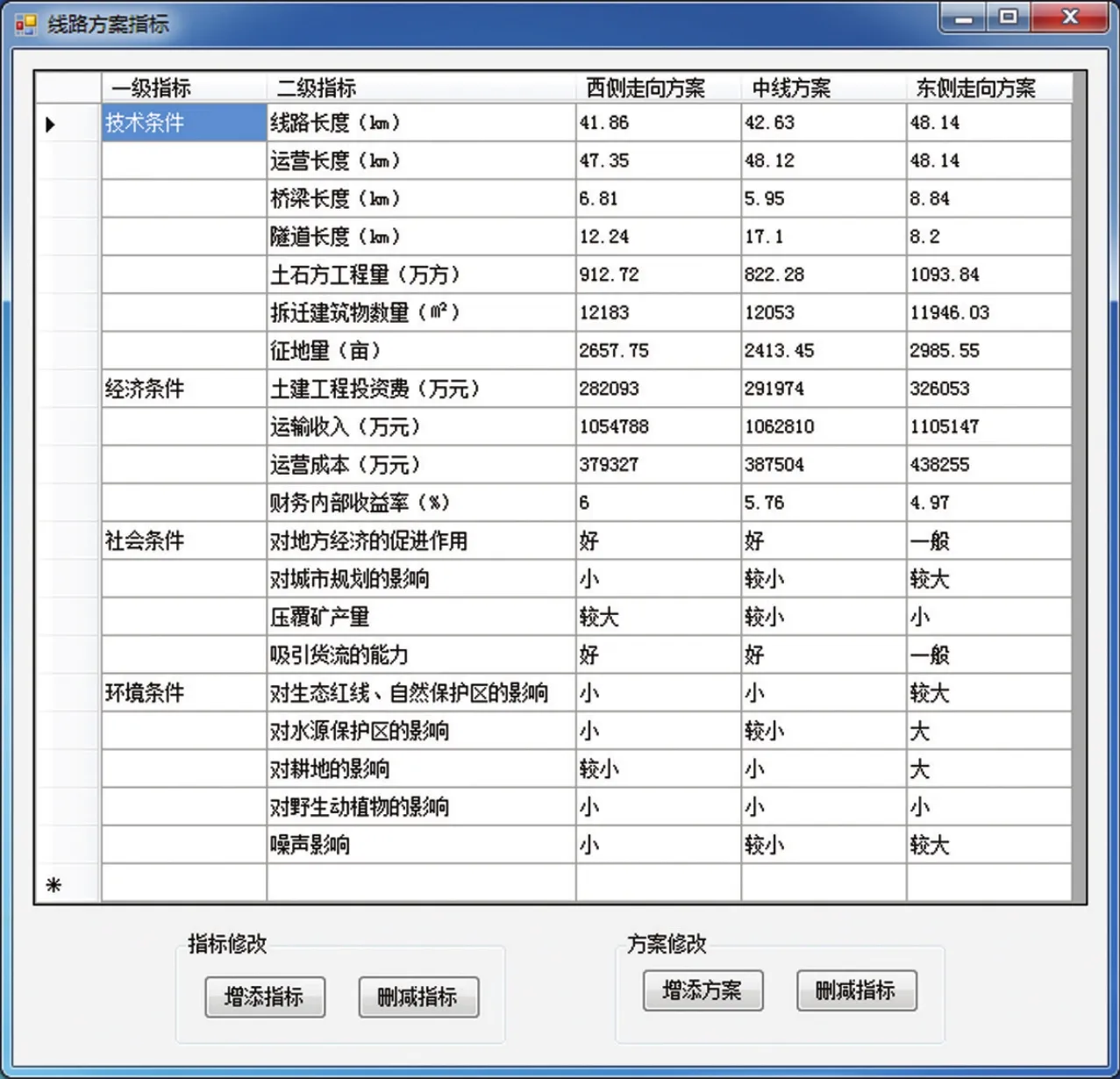
图2 线路方案指标数值及评价水平Fig.2 Values and evaluation levels of indicators for each railway alignment scheme

不同线路方案的优缺点兼具且差异明显，因缺乏明确的指标权重导致难以直接判定各方案孰优孰劣，且部分定性指标也增加了方案评价的困扰。因此，需利用云模型对定性指标进行量化处理，进而基于AHP耦合TOPSIS模型对线路方案进行优选。

由图2可见，影响新建新交口至安泽铁路线路方案优选的20个指标中，技术条件和经济条件指标均为定量指标，而社会条件和环境条件的相关指标均为定性指标，采用云模型理论对其进行量化处理，即根据表1分别对应各指标的期望、论域和熵，根据2.2节的算法，取N= 500，即生成500个云滴，并取其平均值，分别得到社会条件和环境条件中9个铁路线路定性指标的量化取值，由此得到线路备选方案的定量决策矩阵如下。

以上述指标量化矩阵为基础，利用AHP对各指标进行初始常权赋值，即：首先，参照公式 ⑴对同层中指标间的相对重要性进行标度，得到判断矩阵，列举P2—C8 ~C11判断矩阵如表3所示；其次，利用公式 ⑵、公式 ⑶ 计算指标权重，并利用公式 ⑷ 计算各判断矩阵的最大特征根，利用公式 ⑸、公式 ⑹ 对判断矩阵进行一致性检验，各判断矩阵层次分析结果如表4所示。

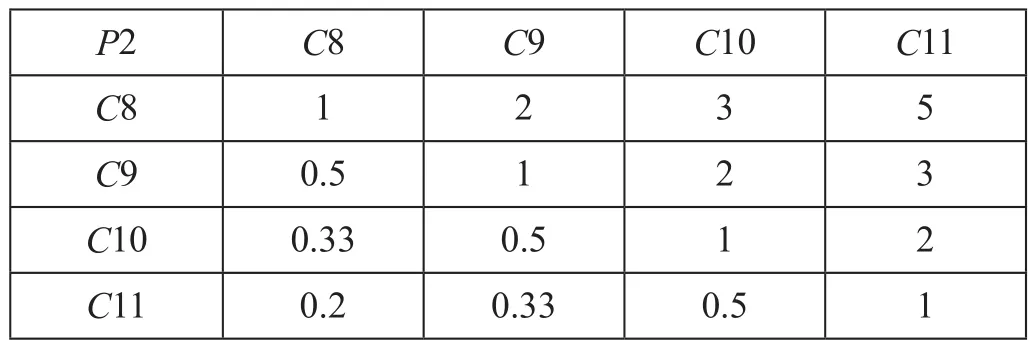
表3 P2—C8 ~ C11判断矩阵Tab.3 P2—C8 ~ C11 judgment matrix

由此，根据表4可得底层指标的权重值，即各指标的初始常权如下。

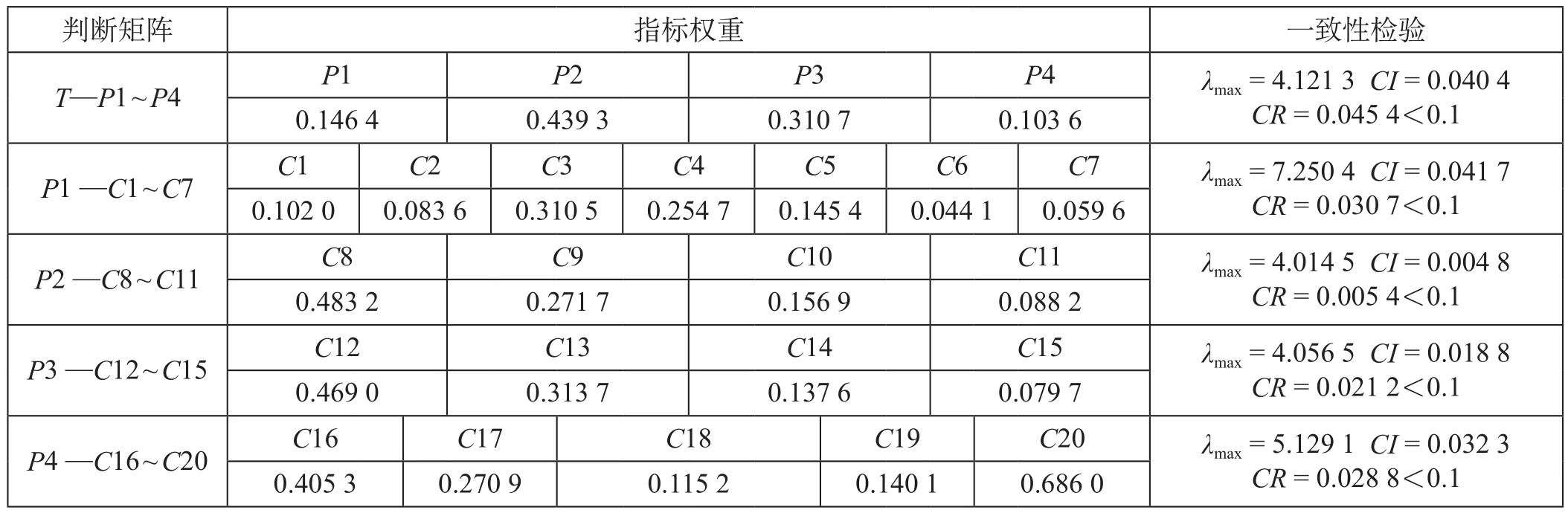
表4 各判断矩阵层次分析结果Tab.4 AHP results of each judgment matrix

图2中，C9，C11 ~C12，C15为正向指标，C1 ~C8，C10，C13 ~C14，C16 ~C20为负向指标，则分别按照公式 ⑻ 和公式 ⑼ 进行标准化处理，并利用公式 ⑽ 计算变权权重如下。

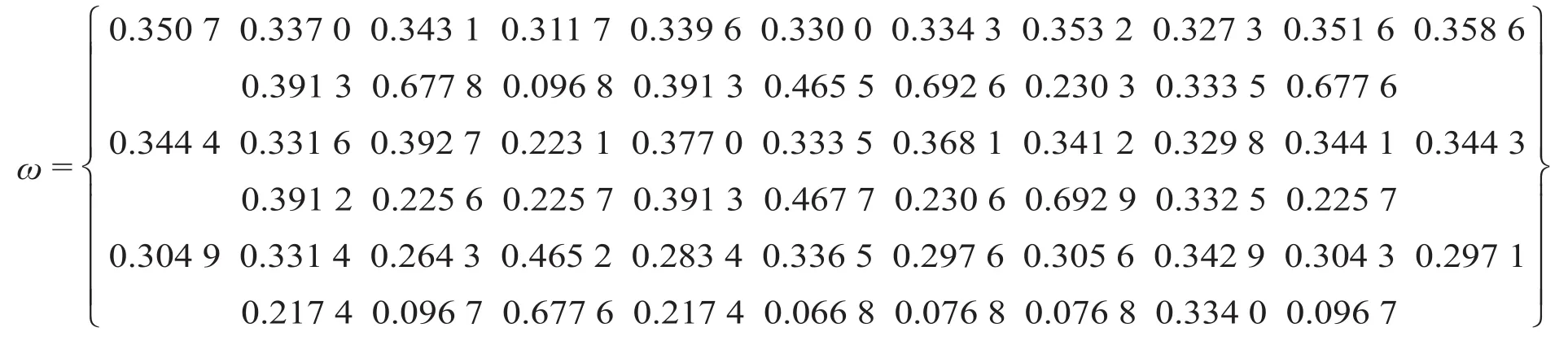
从而，经过变权处理后，进一步利用公式⑾计算得到加权的规范化矩阵，系统输出的加权规范化矩阵如图3所示。

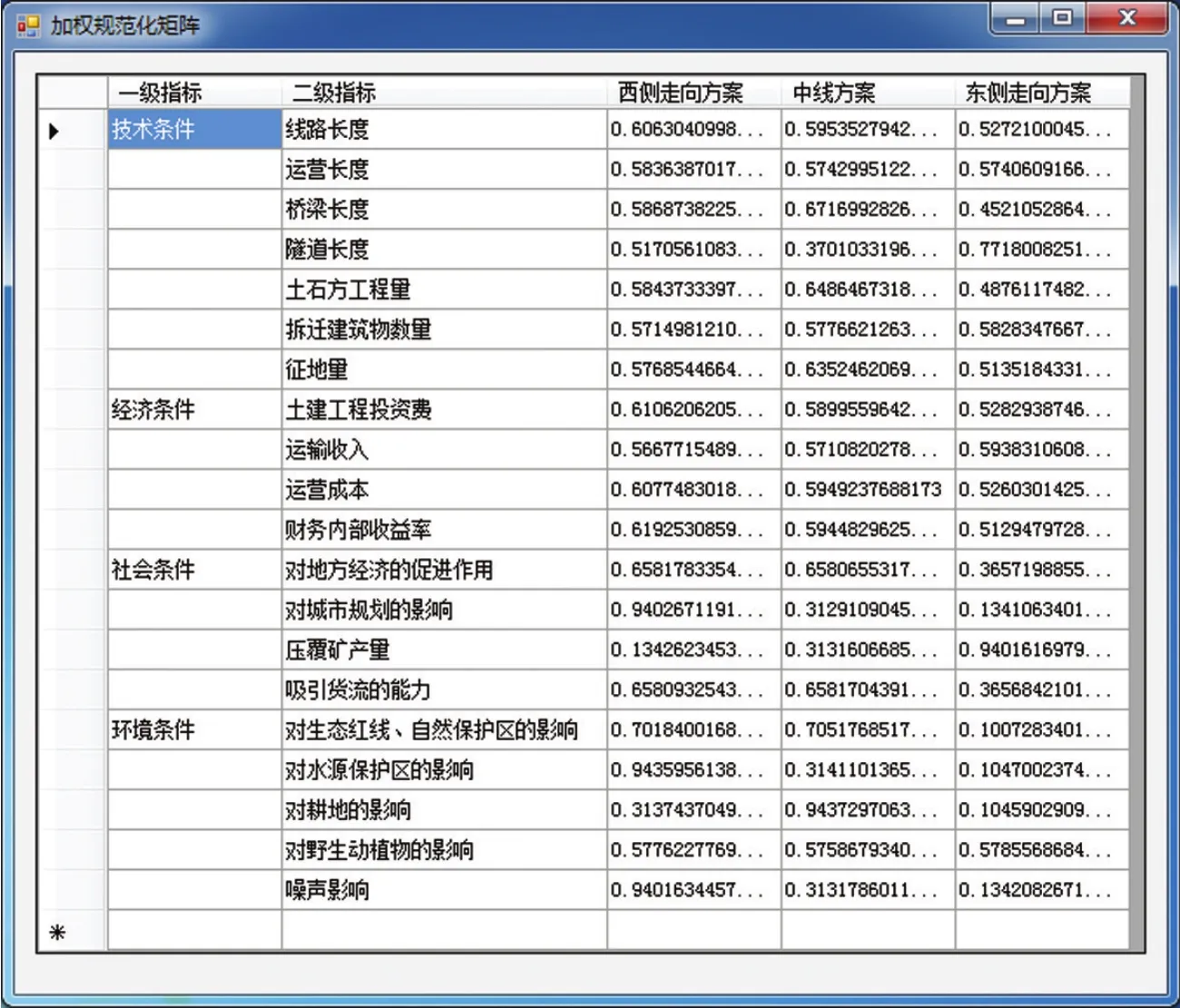
图3 加权规范化矩阵Fig.3 Weighted normalized matrix

基于TOPSIS，按照公式 ⑿、公式 ⒀ 计算各线路方案与正、负理想方案的距离如表5所示。

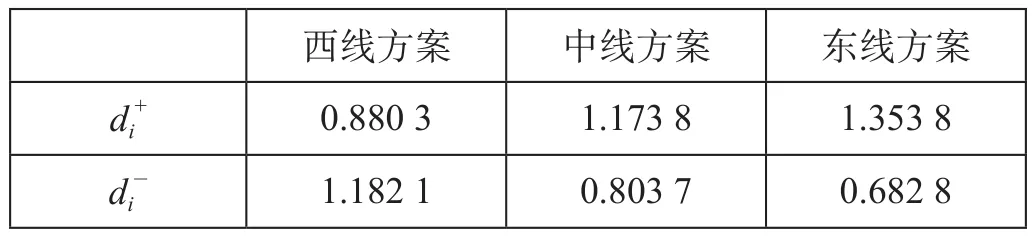
表5 各线路方案与正、负理想方案的距离Tab.5 Distance between each railway alignment scheme and the positive/negative ideal one

最后，利用公式⒁计算各选线方案与正理想方案的贴近度分别为：E1= 0.573 2，E2= 0.406 4，E3= 0.335 3，即新建新交口至安泽铁路西线方案、中线方案、东线方案的综合优越度分别为：57.32%，40.64%，33.53%。因此，通过测算比选，3个线路方案中，西线方案的综合优越度最高，为最佳推荐方案，其次中线方案，再次东线方案，线路方案评价结论如图4所示。

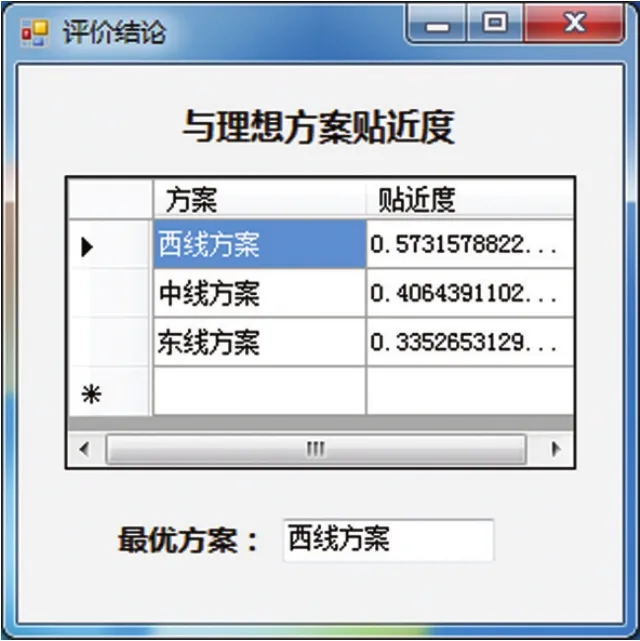
图4 线路方案评价结论Fig.4 Evaluation conclusion of railway alignment schemes

考虑到各线路方案的工程投资差别并不十分明显，其他指标对方案选择的影响同样较为显著，因而实际决策中存在很大不确定性。例如，虽然西线方案里程相对较短、工程投资相对节省，但相比之下，东线方案桥隧比低、工程难度更小，且拆迁量小、压覆矿产少、协调难度更低；而中线方案各方面指标在3个方案中较为折中。这些都成为干扰决策的重要因素。根据模型的综合权衡，通过计算结果可得清晰的评价结论，即西线方案与理想方案的贴近度最近，为3个方案中的最优方案。

基于模型所建立的参数和方法体系，同样可移植应用于其他项目，仅需在针对具体项目的评价指标选取或参数标定方面略作调整即可。

5 结束语

针对铁路线路方案优选问题，充分吸收前人在铁路选线及其他多目标决策领域的研究成果，提出了AHP耦合TOPSIS的解决方法，在铁路线路设计实例中进行应用并取得了较好的决策效果。铁路线路方案优选是一项投资巨大、关系国计民生的基础设施投资重要决策，所需考虑的因素和指标极为复杂，针对特定案例所构建的评价指标体系具有一定的局限性，更具普适性的铁路线路方案评价指标体系仍需进一步完善；另外，所提出的技术方法在AHP的指标间标度设定和定性指标评价打分等方面仍存在一定的人工干预，后续宜进一步结合数据挖掘、人工智能等理论与技术，消除人工干预的影响，进一步提升铁路选线的客观性与科学性。