基于多品类多车种的铁路网重空车流径路联合优化研究

刘海涛，张 巍，秦 胜

（1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081)

0 引言

铁路车流径路贯穿于计划编制、作业组织与成本核算等多个环节，是运输组织的一项重要内容。近年来，随着国家产业结构升级、运输结构调整的持续推进，铁路货源市场形势发生较大变化，货运供需结构波动幅度增大、频率加快，使得路网车流结构发生明显变动[1]；另一方面，货运新线开通、既有线扩能改造以及高速铁路成网建设，提升了既有铁路网的货运能力供给水平。在新的市场格局和路网环境下，统筹考虑运输能力供给与货运需求变化，及时优化车流运行径路，对进一步降低运输综合成本、提高铁路货运市场竞争力具有重要意义。

车流径路优化调整的相关研究起步较早，成果已较为丰硕。刘兰芬等[2]基于最小费用最大流的增广链搜索思想，设计了车流备选调整径路的求解方法，并利用遗传算法实现车流径路调整方案的优选。武威等[3]通过历史统计数据确定车流在途和在站时间消耗参数，基于K短路算法求解出单OD间的合理径路集，并采用Vague集对车流径路进行评价；何世伟等[4]提出点线能力协调的度量方法，并将其纳入车流径路优化的目标函数中；高明瑶等[5]针对既有点—弧模型可能拆分车流且难以准确获取径路的缺陷，对模型进行改进；温旭红等[6]结合铁路车流具有“合而不分”的运行特征，提出基于树形结构的车流径路优化方法；赵娟[7]考虑不同的车流组织模式，构建0-1规划模型实现装车地始发直达车流和零散技术车流的综合优化；孟凡江等[8]针对现行车流径路算法的不足，提出适应铁路运输企业经营管理发展需要的多路径分配模型；刘畅[9]基于公铁运输结构调整与铁路车流组织间的相互影响机理，以公铁两网综合物流成本最小化为目标，对公铁货流转移与铁路车流径路实现联合优化。

既有研究仅侧重于考虑重车车流，而忽视空车车流径路及流量分配的客观存在，具有一定的局限性，特别是在有点线能力限制的路网上，重空车流可能同时运行在同一径路上，空车流不但会占用路网部分能力，而且会影响重车车流径路的选择。此外，路网中重空车流混合运行时，不同品类货物所需的车种类型存在差异，多车种间不可完全代用，故还需兼顾货种与车种间的相互组合[10]。为此，将重车车流按品类进行细分，并引入车货关联辅助系数，以路网中重空车流输送总成本最小为目标，在满足空车车流生成、车流径路唯一性及路网区段能力约束的前提下，构建基于多品类多车种的铁路网重空车流径路联合优化模型，以期从整体上优化路网重空车流走行，进一步提高运输效率效益。

1 基于多品类多车种的铁路网重空车流径路联合优化模型

1.1 建模思路

货物运输需求受经济发展、资源分布以及生产力布局等多种因素的影响，在时空分布上呈现出一定的不均衡性，使得货物运输具有明显的周期性和方向性，进而引起铁路车站的装卸差，正是这种车站间的装卸不平衡造成空车在路网上的流动。空车流作为一种随重车输送而产生的派生需求，尽管在运输时不产生经济效益，但却同样占用路网资源能力，故其会制约重车需求的满足以及货物运输径路的选择。因此，在规划车流径路时，有必要从整体性的角度出发，将重空车流进行统筹考虑。

铁路车流径路和流量分配属于最小费用多商品网络流问题，目前常用的优化模型根据变量定义方式的不同可分为点－弧模型与弧－路模型2类[11]。点－弧模型是以路网的站点和弧段为对象设置变量的，而弧－路模型则是以路网弧段和OD径路为研究对象，将决策变量定义在各个OD车流的可行径路上，这为空车流生成与径路分配创造了有利条件。因此，针对既有车流径路寻优时将重空车流相分离的局限性，将弧－路模型与空车调配模型进行底层融合，构建重空车流径路和流量分配的一体化优化模型，从而使新模型考虑因素更加全面，优化效果更加显著。

1.2 模型构建

受车流径路优化问题业务关联程度高、计算规模庞大、数据来源不畅等因素制约，为简化实际问题的复杂程度，提出以下假设：①铁路网络与OD车流均已完成归并，形成了支点间的路网结构与车流集合；②模型中的弧段服务能力是综合该区段内线路、车站、机务等设备，并扣除旅客列车占用后计算得出的；③相同OD间的车流径路具有唯一性，不可对车流进行拆分运输。

在给定铁路网图G= (V，E)的条件下，定义模型相关符号及含义如表1所示。

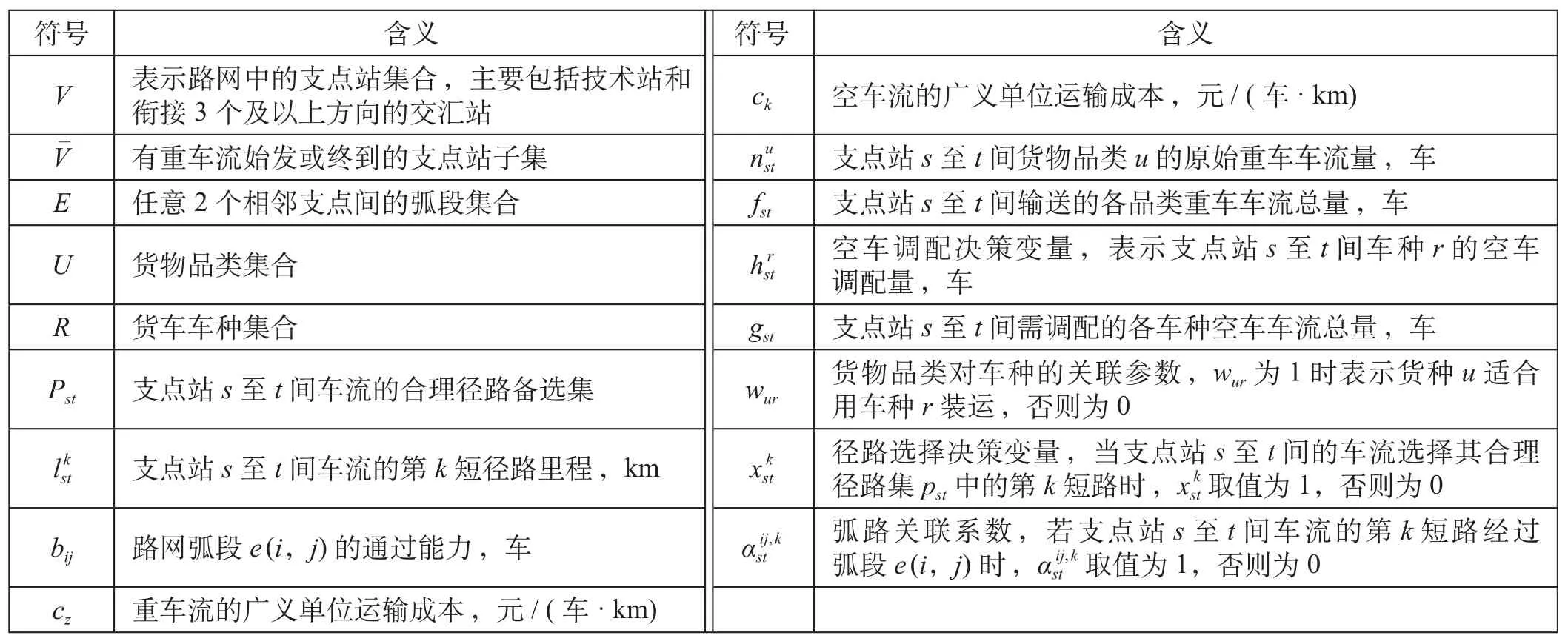
表1 模型相关符号及含义Tab.1 Symbols and meanings of the model

铁路网重空车流径路联合优化模型综合考虑了重车流和空车流间的相互转换关系，以路网重空车流流量与其单位运输成本乘积之和最小化为目标，实现重空车流径路以及分车种空车调配方案的优化生成，目标函数为

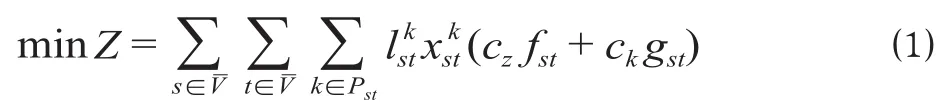
重车的形成需要充足的空车保障，故将重车流的起始站视为空车需求站，而重车流在终到站卸后又会产生空车，所以将重车流的终到站视为空车供给站，同时车货关联系数wur的引入体现了不同品类货物与空车车种的适装关系，能够满足分车种实行空车调配的需要。因此，空车流的生成条件为

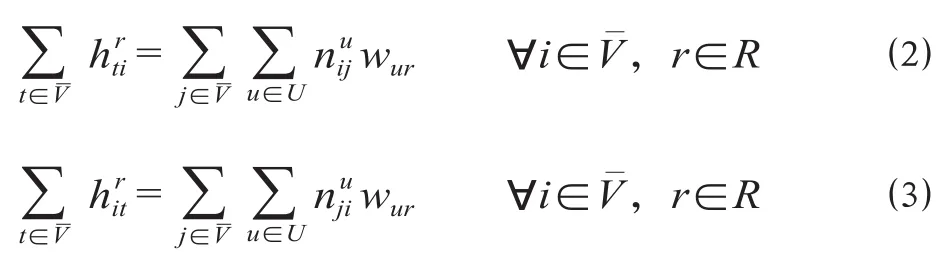
任意两支点站间的重车总流量等于各品类重车流量之和，空车总流量等于各车种空车流量之和。

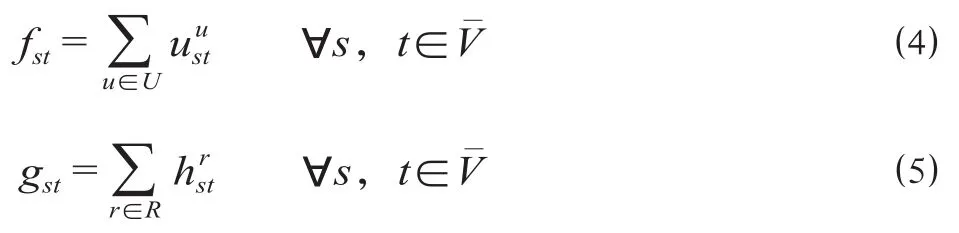
相同OD间的车流在起始站到终到站的输送过程中，只能够选择备选径路集中的1条路径，不可对其进行拆分运输。

路网各弧段需满足一定的负荷要求，即应保证各弧段的重空车流流量不得超出其能力限制。

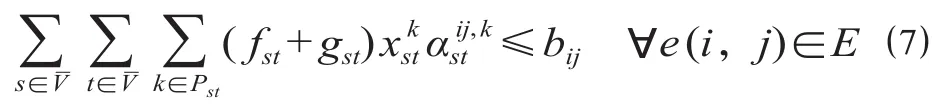
由此可见，该模型依据空车流的形成机理，对铁路网空车调配和车流径路优化2个问题进行了巧妙融合，在弧－路模型的基础上添加决策变量可以生成空车流的流量流向，结合原模型的径路决策变量又能够保证同时获取路网重空车流径路。此外，引入车种和货物品类间的关联系数wur，体现了不同品类货物对空车类型的选择，使得所构模型能够满足多品类多车种的重空车流径路联合优化的需求。

1.3 模型求解

针对构建的重空车流径路联合优化模型，设计求解思路具体如下。

步骤1：重构车流OD集合。将支点站集合中的元素两两组合，重新构造重空车流OD集合以缩减模型求解规模。

步骤2：生成合理备选径路集。根据给定的路网结构和弧段参数，调用双扫描算法(Double Sweep)，计算车流fst的广义K短路里程，并生成相应OD车流的合理备选径路集P= {pst=

步骤3：建立弧—路关联矩阵。遍历合理径路集P，依次判断车流fst的第k短径路是否包含弧段e(i，j)，若包含则取1，否则取0，据此建立弧段与径路间的关联关系矩阵其中card(E)。

步骤4：参数输入求解计算。将路网结构、重车流与合理径路集等数据导入数学规划优化软件中进行编码求解。

2 算例分析

以我国东北地区局部铁路网为例，模拟分品类的货运OD需求数据，基于软件平台编程实现对模型的精确求解，得出优化的重空车流径路及空车调配方案，并与分步优化结果进行对比分析，从而验证构建的重空车流径路联合优化模型的有效性。

2.1 基础数据

算例中的货运支点网络图如图1所示，包含14个支点车站和20条弧段，假设每条弧段的上下行能力均相等。为体现模型对重车品类与空车车种的考虑，模拟生成该地区煤炭、金属矿石、矿建材料、粮食和石油5种货运品类的OD运量，同时在不考虑车种代用的前提下，按照货种与车种最适宜的组合关系，对于煤炭、金属矿石和矿建材料用敞车装运，粮食用棚车装运，石油则用罐车，分品类的重车OD车流量如表2所示。根据重空车流间的相互转换关系，结合各品类OD重车流数据，汇总得出各支点站分车种的装卸车数量如表3所示。路网中重空车流的单位运输成本cz与ck取值分别为1.2和0.6。

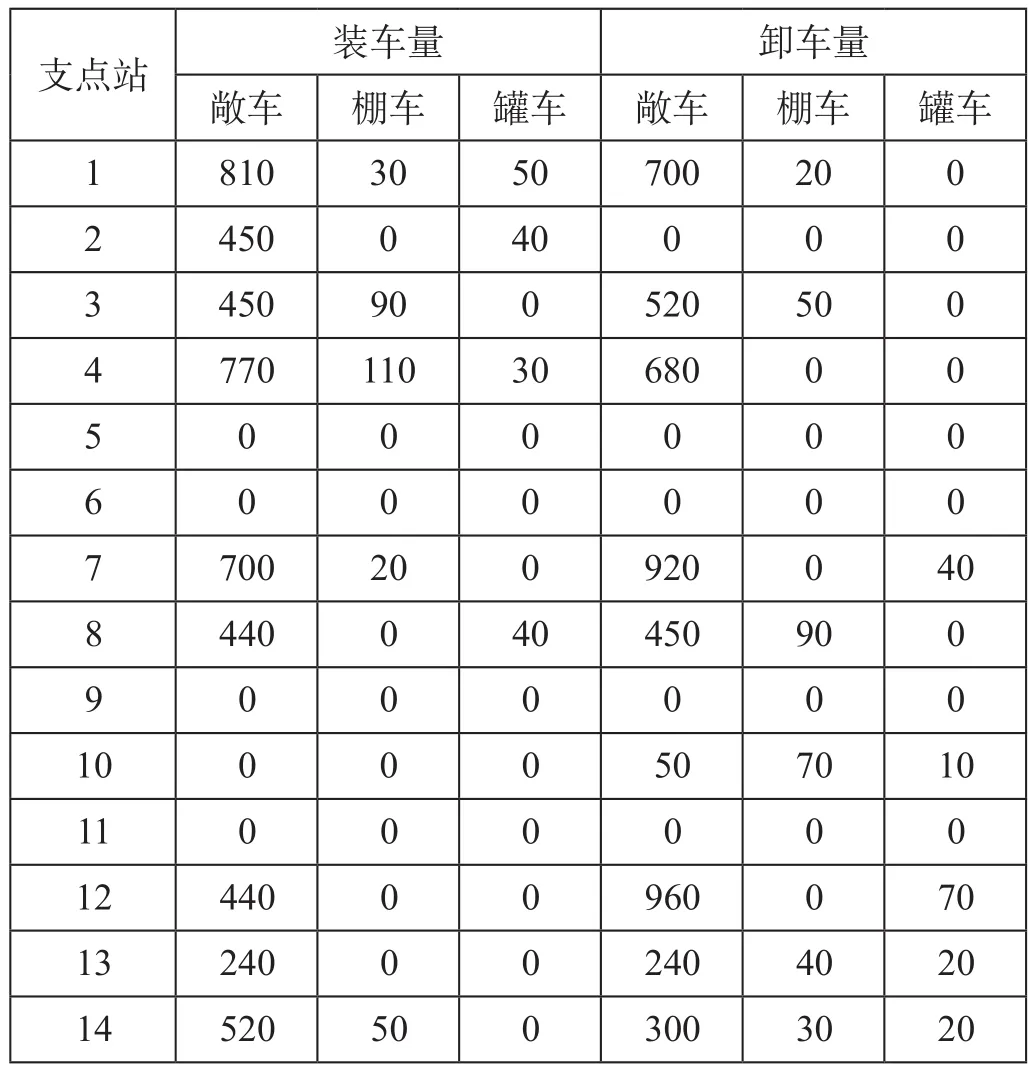
表3 各支点站分车种的装卸车数量 车Tab.3 Number of loading and unloading wagons at each fulcrum station by wagon type

图1 货运支点网络图Fig.1 Network of freight fulcrum

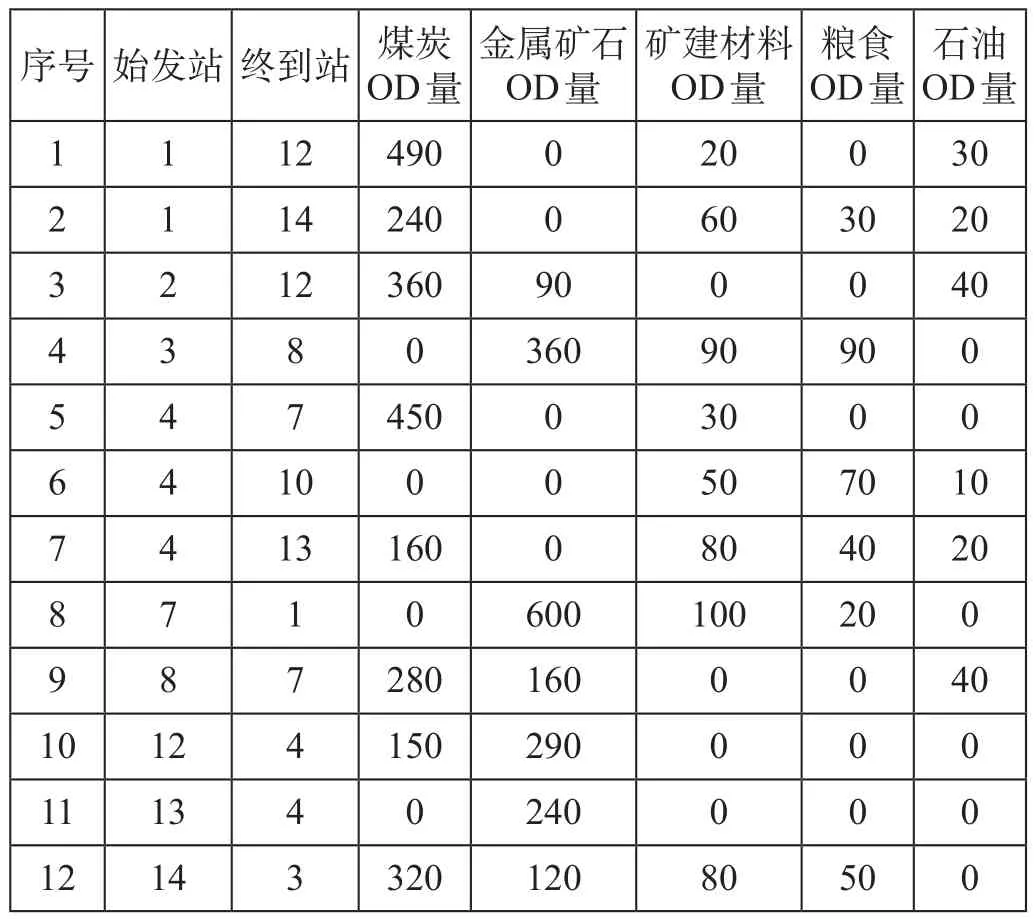
表2 分品类的重车OD车流量 车Tab.2 OD traffic flow of loaded cars by freight category

2.2 结果分析

基于数学规划优化软件中的全局最优求解器，实现对联合优化模型的精确求解。计算结果显示，根据各品类重车流的流量流向情况，优化形成了路网中较为合理的空车调配方案，生成21对不同站点间的空车供需OD关系，各OD间分车种别的空车调配结果及运行径路如表4所示。由表4推算出，区域路网共计5 280车的重车运量需求中，有3 710车可以通过本地卸后形成的空车就地装车，自装自卸占比为70.27%。空车调配方案中并没有产生同种空车的对流运输现象，且符合多车种调配的现实需求，例如支点站4日均发送110车粮食，所需的棚车可由支点站8，10和13共同提供，而日均发送30车石油所需的罐车则可由支点站12和13提供；又如重车流14—3日均520车的敞车需求中，有300车来源于本站的自卸空车，剩余220车分别来源于支点站10，12和13。

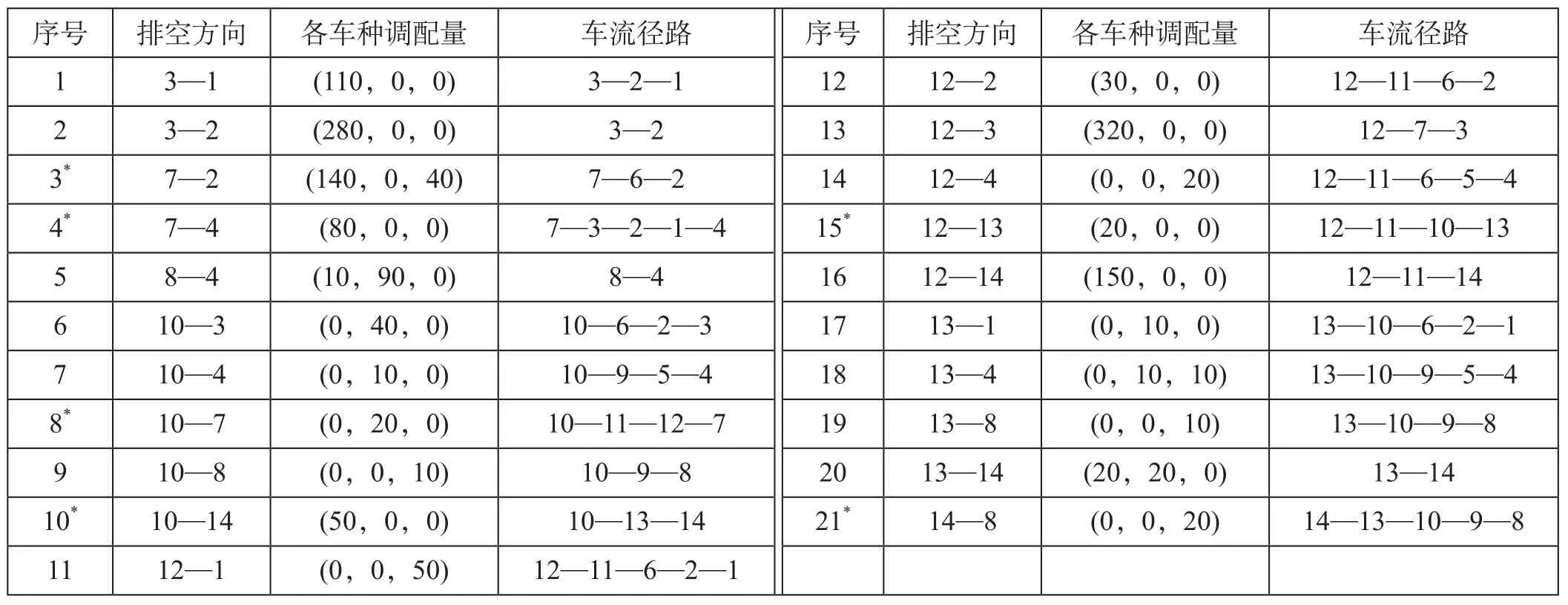
表4 空车调配结果及运行径路Tab.4 Empty car distribution results and operation routing

在路网局部弧段能力受限的情况下，部分重空车流将无法走行最短径路，而需绕行至特定的径路进行运输。重车车流径路优化方案如表5所示，可以看出，重车流2—12，4—10，7—1，8—7和14—3均存在不同程度的绕行，绕行距离分别为38 km，101 km，55 km，164 km及199 km。除重车外，空车流7—2，7—4，10—7，10—14，12—13和14—8也无法按最短径路输送。重空车流总运输成本为529万元，相较于无能力限制条件下完全按最短径路运输总成本的498万元，车流绕行带来成本增加为31万元，也从侧面反映出缩短车流径路对降低运输成本具有重要作用。

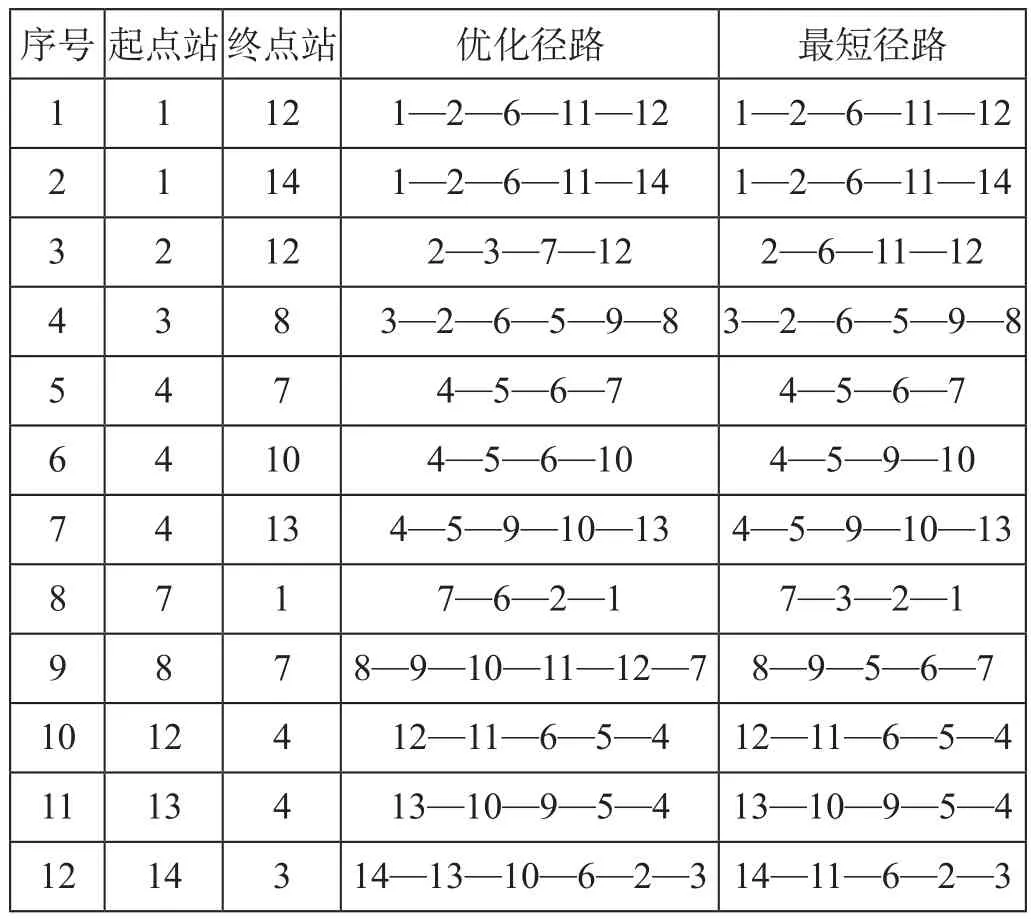
表5 重车车流径路优化方案Tab.5 Optimization scheme of loaded car flow routing

按优化生成的径路对重空车流进行流量分配，得出各弧段能力利用情况如图2所示。可以看出，大部分区段的能力得到了充分利用，但受资源分布不均衡的影响，使得路网货源货流呈现出明显的方向性，故会存在部分区段上下行能力利用不平衡的现象。同时，配流结果也更直观地反映了区段瓶颈状况，可以为路网的扩能改造及货源吸引提供参考依据。

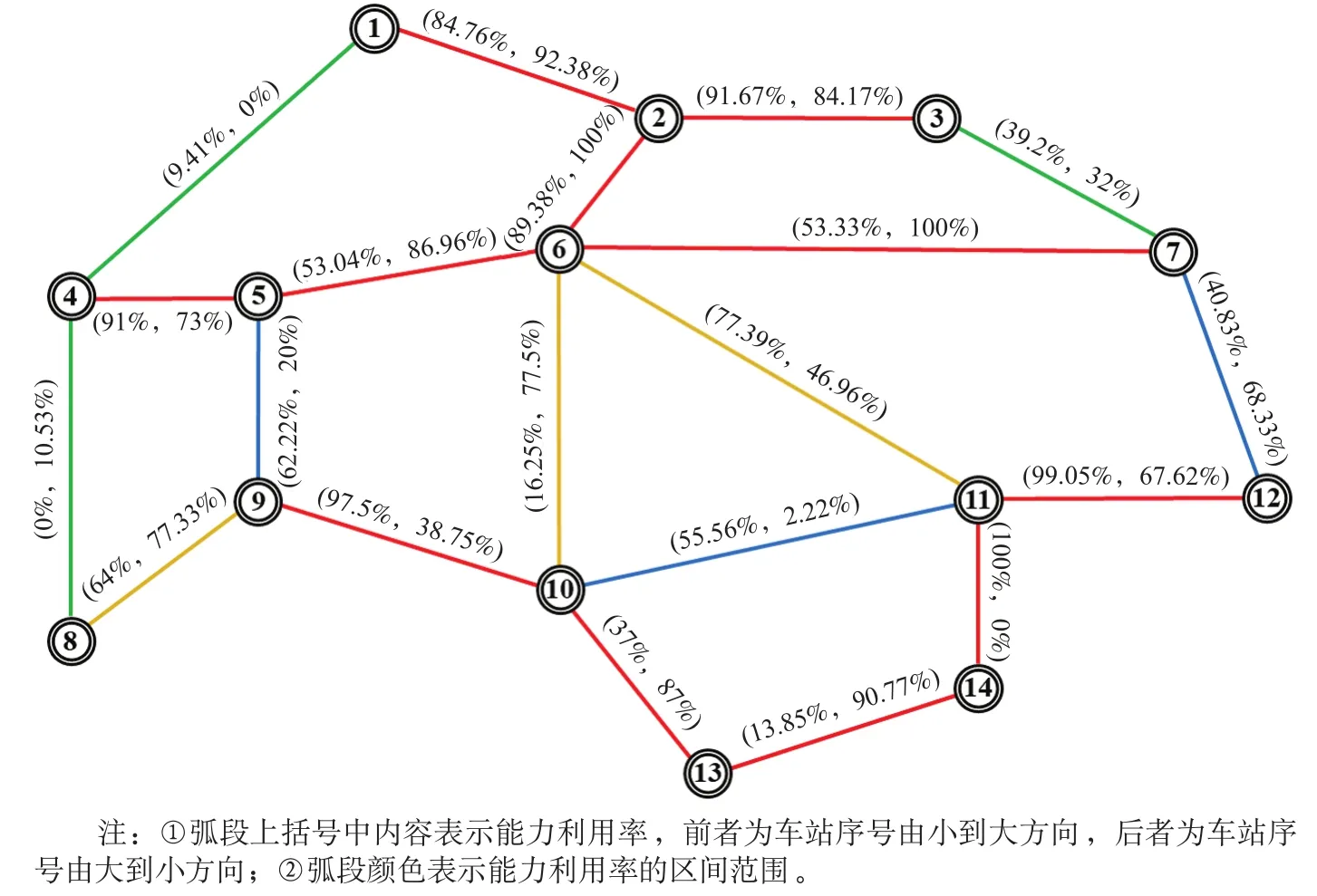
图2 各弧段能力利用情况Fig.2 Capacity utilization of each arc

在规划重车车流径路时，若不考虑空车流的影响，可能会导致高估路网能力，使得部分重车流最终无法按规定的径路输送，而以往研究往往采用分步优化的处理方式，即先按最短路扣除相应空车能力占用，再进行重车流径路的优化。基于此，为体现联合优化模型的优越性，对2种优化策略下的相关统计指标进行对比，相关指标对比情况如表6所示。可以看出，联合优化虽小幅增加了空车走行公里，但使得重车平均绕行率从10.67%降低至6.93%，总运输成本从541万元降低至529万元，对缩短重车流绕行，降低总运输成本具有积极作用。

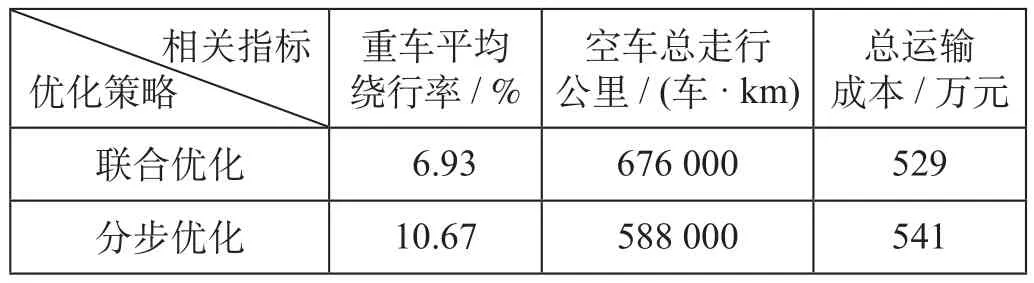
表6 相关指标对比情况Tab.6 Comparison of related indicators

综合分析可知，研究提出的联合优化模型在求解后不仅能够同时获取分车种空车调配方案以及重空车流径路方案，还能掌握路网区段的能力利用情况。相较于以往仅针对重车流的径路优化分配方法，基于多品类多车种的铁路网重空车流径路联合优化模型考虑因素更加全面、优化效果更加显著，具有较强的应用前景。

3 结束语

车流径路是指导铁路车流组织的重要依据，在新的市场形势与路网环境下，统筹考虑运能供给与货运需求的动态变化，及时对车流径路进行优化调整，对提高路网能力利用水平、降低运输综合成本、提高铁路货运市场竞争力具有重要意义。针对既有车流径路优化模型的局限性，将多车种空车调配纳入车流径路优化体系，实现重空车流径路和流量分配的一体化寻优，使得优化结果更加贴近实际情况，具备较强的实践应用前景。在今后的研究中，亟需从车流径路精细化管理需求入手，探索车流径路与货运营销、计费径路和编组计划等协同优化技术。