前馈补偿和自适应遗传算法的空调系统优化

杨世忠，李善伟，孙崇国

(青岛理工大学信息与控制工程学院，山东 青岛 266520)

1 引言

变风量空调起源要追溯到上世纪80年代的美国，变风量空调凭借其节能、高效、使用灵活等特点广受人们的青睐[1]。随着变风量空调系统的发展，一些弊端也逐渐显露出来，例如当多个回路同时工作时，系统存在较强的耦合，严重影响了系统的稳定运行[2]。传统的变风量空调系统采用PID控制，PID控制算法原理简单、使用方便、鲁棒性好，但是其控制品质对被控对象变化不敏感，控制精度和快速性都不高[3]；随着科技的发展，越来越多的智能算法应用到实际的工程实践当中，比如模拟退火算法、遗传算法、粒子群算法，神经网络算法等。基本遗传算法是通过模拟达尔文生物进化理论中的自然选择和遗传学中的计算模型相结合的全局优化寻找最优解的算法[4]。文献[5]提出了一种基于粒子群优化算法和遗传算法相结合的多子群混合算法(HGA-PSO)。该算法采用分层结构，底层由一系列遗传算法组组成，提高了算法的全局搜索能力。上层由各子群最优个体组成，采用粒子群优化算法的初速来提高局部搜索的精度。研究分析表明，该算法具有全局收敛性，并对七个典型的高维Benchmark函数进行了测试，仿真结果也同样表明该算法的优化性能优于其它测试算法[5]。文献[6]提出了一个基于嵌入的永磁同步电动机的数学模型的一种基于遗传算法的参数辨识方法。该方法使用的信号都是可以直接检测到的状态变量，从而减少了其它扰动对电机参数辨识的影响，提高了参数辨识的精度。仿真结果表明，通过使用遗传算法进行参数辨识鲁棒性好，收敛性好[6]。遗传算法因其对种群优化目标要求低和全局性收敛好而被大量应用，但是其全局搜索能力较弱，容易使算法早期陷入局部最优解[7]。

针对遗传算法的缺点，采用自适应遗传算法进行弥补，主要从初始种群分析、个体适应度缩放、交叉、变异概率的自适应调整、保留优良个体这四个方面进行改进。将基本遗传算法优化的PID控制器和改进的自适应遗传算法优化的PID控制器分别对变风量空调系统的冷冻水流量-送风温度、房间VAVOX风阀开度-房间温度、风机频率-风管静压这三个控制回路进行仿真研究。仿真结果表明，改进的自适应遗传算法相比较传统遗传算法在寻找最优化问题上的效率和准确性都有了大幅度的提高，减少了系统的超调量和调节时间，同时具有较强的抗干扰性和鲁棒性。

2 基本遗传算法

基本遗传算法是通过模拟达尔文生物进化理论中的自然选择和遗传学中的计算模型相结合的全局优化寻找最优解的算法。基本遗传算法的运算过程主要包括染色体编码、产生初始种群、适应度函数、选择、交叉、变异六部分[8]。

1)染色体编码

遗传算法解决问题的关键是染色体编码，因为不同的编码方式将决定染色体的排列顺序。此外，不同的染色体编码方式还将对交叉、变异算子和选择算子产生一定的影响[9]。

2)产生初始种群

随机生成N个串结构数据组成一个种群，遗传算法以这N个串结构数据进行迭代运算，设置计数器最小数字0，设置最大进化代数；

3)适应度函数

用来衡量个体适应度值的函数称为个体适应度函数[10]，适应度函数值的大小与遗传给下一代的个体数成正比，所以适应度值非负，把目标函数化为适应度函数尤为重要。为了对适应度函数进行优化，通常采用指数、线性、代数等变换方法来调节适应度函数的大小以此来提高遗传算法在实际运算过程中的收敛速度。

当求解待优化问题的全局最大值时，按式(1)进行转化；

(1)

4)选择

根据个体适应度值的大小进行选择，适应度值大的个体将会有更高的几率传给下一代，而适应度值较低的个体根据优胜劣汰准则很大概率将会被淘汰[11]。通过选择可以避免优良性状的缺失，从而提高全局收敛性。假设种群大小为M，其中个体I具有适应度值为Fi，则该个体I被选中的概率P为

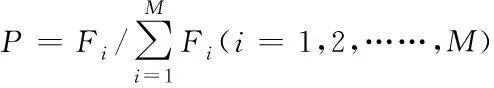
(2)

5)交叉

遗传算法的核心内容是交叉运算，通过不断的交叉操作可以得到新的个体，将种群中的每个个体进行交叉运算有利于提高遗传算法的优化效率。

6)变异

种群中个体以一定的概率转换为该基因座的其它等位基因形成新个体的过程称为变异。通常变异概率Pm非常小，在0.01～0.1之间，变异为新个体的生成提供了机会。

遗传算法因其对种群优化目标要求低和全局性收敛好而被大量应用，是一种全局搜索最优解的自适应算法。其次，遗传算法通过适应度函数和优胜劣汰机制对个体进行选择。其运行过程具有随机性、广泛性、并行性等特点，但也具有诸多缺点：

1)本遗传算法全局搜索能力较弱，容易使算法在早期陷入局部最优解，控制精度不高。

2)基本遗传算法的初始种群是随机的，故而后期算法运行效率很低。

3)基本遗传算法很难确定变量精度和编码长度何者为最优，为二进制编码增加了难度。当增加编码长度，变量精度能满足要求，但运算量会增加；降低编码长度，变量精度就很难得到保证。

4)交叉算子和变异算子在整个算法运行过程中保持不变，这与实际应用相矛盾，同样会对算法的运算效率产生不利影响。

3 自适应遗传算法

针对以上遗传算法的缺点，采用自适应遗传算法进行弥补，主要从初始种群分析、个体适应度缩放、交叉、变异概率的自适应调整、保留优良个体这四个方面进行改进。

3.1 初始种群分析

基本遗传算法的初始种群大都是随机生成的，这样会影响后期算法的运算效率，下面将用两种方法改变初始种群。

1)人为设定初始种群规模

该方法是基于有一定的经验知识的基础上，通过函数运算等方法来获得初始种群，这样提高了初始种群的质量，为后续算法运算提供了基础。

2)小规模群体竞争

该方法初始种群是随机生成的，然后在利用个体适应度函数将个体适应度值大的个体挑选出来组成新的种群，提高了种群的质量。

3.2 个体适应度值的缩放方法

假设某个个体的适应度值为Fi，那么该个体被选中的概率Pi为

(3)

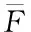
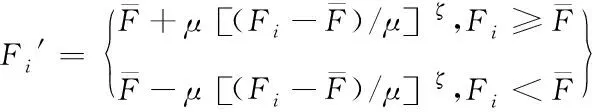
(4)

上式(4)中，ζ代表缩放度，取值范围为(0.5～1)，而μ则按式(5)计算

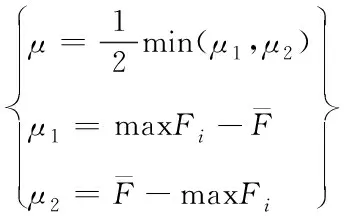
(5)

3.3 交叉、变异概率自适应调整

随着遗传算法运算代数的逐渐增加，交叉、变异概率在这个过程中不断自我调整的过程称为自适应遗传算法[12]。交叉算子Pc和变异算子Pm的值将直接影响遗传算法的收敛速度。Pc越大，种群中新个体产生的速度就越快，但是如果Pc过大，遗传算法的优良模式将会被破坏。与此同时，如果Pc过小，遗传算法的搜索速度就会变得缓慢，甚至停止不前；Pm过大，遗传算法就成了一种随机的搜索算法，失去了遗传算法的优势[13]。但当Pm过小，遗传算法产生新个体的能力减弱，不容易产生新的优良的个体。自适应遗传算法能够根据算法运行的不同阶段调整交叉算子Pc和变异算子Pm的值，不仅能够保证种群进化的多样性，而且算法的收敛性也得到了保证[14]。

交叉算子概率Pc和变异算子概率Pm的调整公式为

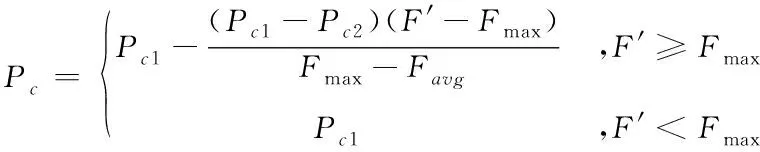
(6)

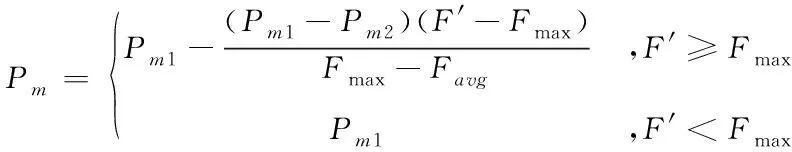
(7)

式中，Fmax为进化过程中个体适应度函数最大值；

Favg为进化过程中个体适应度平均值

F′为两个个体中较大个体的适应度函数值；

F为待变异运算的个体适应度函数值；

Pc1>Pc2>Pc3，Pm1>Pm2>Pm3且为区间(0，1)内的某个值，在优化过程中自适应调整。

3.4 保留优良个体

种群中的个体在进行交叉、变异运算结束后，再计算个体的适应度值。根据适应度值的大小进行淘汰。适应度值大的个体保留下来，小的个体就被淘汰。交叉和变异用于生成新的个体，但不是所有新的个体都是最优个体，所以本文采用优良个体保留策略。只有这样算法产生的所有个体都是最优个体，使算法按照进化方向进行。

4 变风量空调系统建模

图1是本文所要研究的变风量空调系统结构示意图。风系统主要由系统由空气处理单元(AHU)、新风阀、回风阀、排风阀、变风箱和风道网组成。控制循环是由四个控制回路组成：它们分别是送风机频率-风管静压回路、冷冻水流量-送风温度回路、1#VAVBOX阀门开度-1#房间温度、2#VAVBOX阀门开度-2#房间温度，四个循环回路。

图1 变风量空调系统组成

首先，根据机理分析可得到每个回路的机理模型，其次，采用阶跃响应法结合机理模型的结构和阶次可得到相应的特性参数，最后得到该系统的数学模型。该模型是一个四输入四输出的矩阵结构：冷冻水阀开度u1(输入1)，送风机频率u2(输入2)，1#房间VAVBOX风阀开度u3(输入3)， 2#房间VAVBOX风阀开度u4(输入4)，送风温度y1(输出1)，风管静压点静压y2(输出2)，1#房间室内温度y3(输出3)，2#房间室内温度y4(输出4)。由上面可知：输入向量为：U=[u1，u2，u3，u4]T，输出向量Y=[y1，y2，y3，y4]T。则该系统的传递函数矩阵为

(8)

式中，Gij(s)(i=1，2，3，4；j=1，2，3，4)为输入量i和输出量j之间的传递函数，该矩阵的结构为4×4型，共有16个传递函数，改变其中一个输入uj，同时使其它输入量保不变的情况下，由yi对uj的响应得到Gij(s)。

5 前馈解耦控制器设计

图2是带有解耦补偿单元的变风量空调系统多变量解耦的控制框图。D(s)可由(9)给出。

(9)

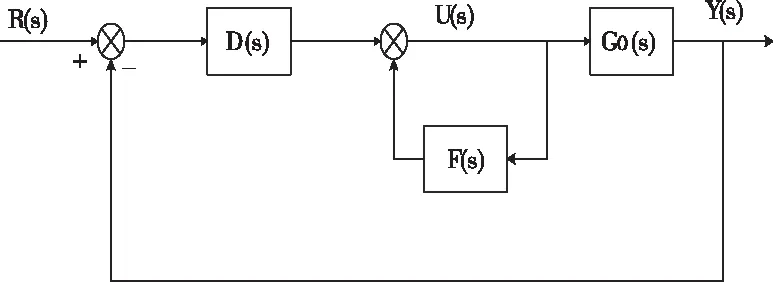
图2 变风量空调系统解耦控制框图

F(s)可以描述为

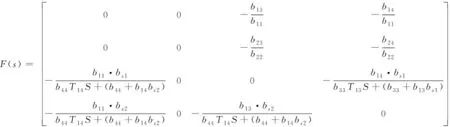
(10)

传递函数矩阵WKD(s)可由式(11)得出

WKD(s)=G0(s)[E-F(s)]-1D(s)

(11)

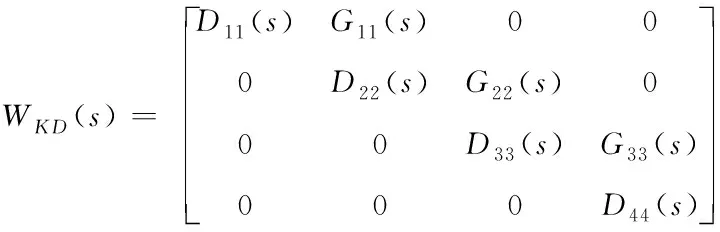
(12)

传递函数矩阵WBD(s)可由式(13)得出

WBD(s)=[1+WKD(s)]-1WKD(s)

(13)

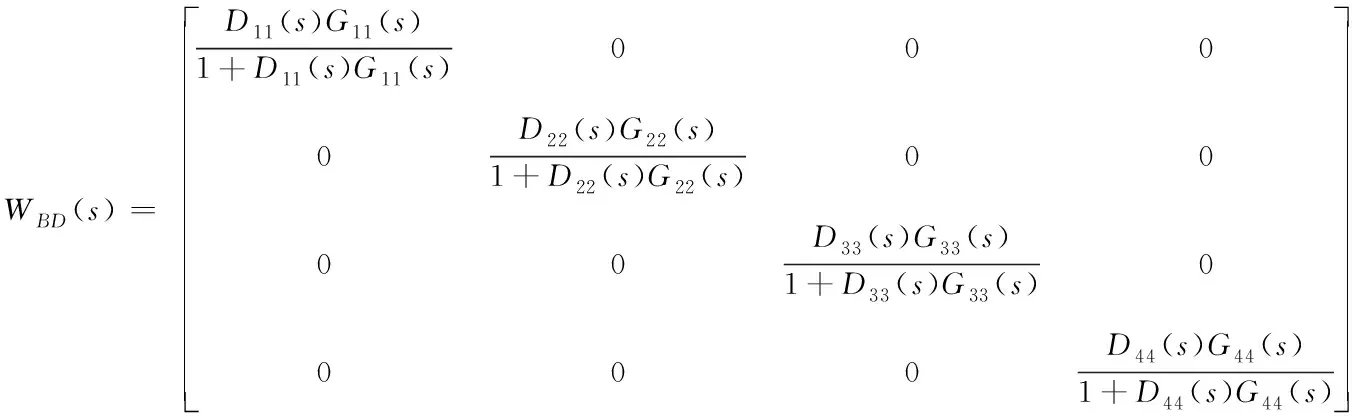
(14)

为矩阵G0(s)的主对角元素。由以上可知，前馈补偿解耦单元可以将系统的开环和闭环传递函数矩阵变为对角矩阵，从而消除了四个控制回路之间的耦合，实现了变风量空调系统的解耦控制。

6 变风量空调系统优化控制仿真

本文通过前馈补偿解耦和自适应遗传算法相结合的方法对变风量空调系统的四个回路进行优化控制。图3为解耦环节采用前馈补偿，控制环节采用基本遗传算法优化的变风量空调系统响应曲线，图4为解耦环节采用前馈补偿，控制环节采用改进的自适应遗传算法优化的变风量空调响应曲线。

图3 基于基本遗传算法优化的变风量空调系统响应曲线

图4 基于改进自适应遗传算法优化的变风量空调系统响应曲线

通过图3到图4对比可以看出，经过改进的自适应遗传算法优化的变风量空调系统的控制效果明显优于基于基本遗传算法优化的空调系统响应曲线，具体表现为：房间温度实际值基本维持在设定值附近且波动范围较小。当房间温度设定值发生变化时，送风温度和风管静压会有一定的偏移量，但是经过改进的变风量空调系统的送风温度和风管静压设定值偏移量明显小于未经改进的变风量空调系统的送风温度和风管静压值。总体来说，经过改进的变风量空调系统的冷冻水流量-送风温度、风机频率-风管静压、1#房间VAVOX风阀开度-1#房间室内温度、2#房间VAVOX风阀开度-2#房间室内温度这四个耦合回路基本实现了解耦，优化效果较理想。

7 结论

本文针对变风量空调系统多变量、非线性、强耦合等特点，基本遗传算法在参数优化方面存在缺陷，采用自适应遗传算法进行弥补，主要从从种群分析、个体适应度值缩放方法、交叉概率和变异概率的自适应调整，保留优良个体这四个方面进行改进。最后将基本遗传算法和改进的自适应遗传算法分别对变风量空调系统的冷冻水流量-送风温度、风机频率-风管静压、房间VAVOX风阀开度-房间温度这三个控制回路的PID控制器进行参数优化控制。仿真结果表明在对变风量空调系统进行控制时，相比较基本遗传算法，采用前馈补偿和改进的自适应遗传算法优化的控制器能有效地补偿变风量空调系统各回路之间的耦合关系，保证了系统的稳定运行，为变风量空调系统的优化控制提供了一种可行性的解决方案。